实现多元合一有效融入STEM教育理念
◇任宝生(甘肃:泾川县玉都镇郭马村小学)
STEM 教育理念最早源于20世纪中期的美国,其在当时属于科学教育领域较为先进的理念之一。近些年,STEM 教育理念传入我国,并在原先的基础上对其进行了一定程度的修改,最终形成了一套适合我国当前教育形势、有着发展价值的教育理论体系,并越来越成为当前教育的主流思想。STEM 包含了科学、技术、工程、数学四个不同的领域,而且,不仅仅是对这四个领域内容的简单概括,还将它们汇聚成了一个有机的整体,实现了真正意义上的多元合一。这一教育思维也值得广大教育工作者在教学的其他领域中参考借鉴,以达到相同的效果。
一、贯彻STEM教育理念,突显教学融合价值
要想在教学中有效贯彻一种新的教学理念,首先必须找准它的理论方向,其主要依据便是该理论的基本思想与主要目标。顺着这些线索前进,自然能够将其有效应用于教学实践,充分体现其对教学的实际价值。
(一)认清规律,降低教学难度
例如在小学数学(人教版)二年级上册第7 课《认识时间》的教学中,时间是一个相对抽象的概念,虽然时间每时每刻都在流逝,但我们无法直接观察时间的变化。因此,教师教学时间这一概念就显得格外困难。为了让学生理解时间流逝的本质及其对应的速度,就引入了钟表这一工具。学生只要观察钟表上数字的变化,就知道时间流逝的快慢和多少,发现时间的规律。认清时间概念之后,学生在后续的学习及练习中,也能更好地发挥,实现认识水平和学习成绩的提升。
上述方式,也是对STEM 教育理念的把握,突出了规律的发现与运用对教学开展的作用。在小学数学教学中,还存在大量概念理解性内容。教师要充分利用这种思维,为学生建立知识点系统性的理论框架,帮助学生打好数学基础。
(二)巧用多种工具,开拓教学途径
STEM 教育理念强调,要脱离传统教学模式的各项限制,灵活使用现代化工具,开展新时代教学。随着时代的发展,近年来涌现出了许多新型的信息工具,如电子白板、平板电脑、学习机等。教师在教学中,要主动使用这些工具,帮助学生掌握各知识点以及数学学习和解题的高效方法。
以小学数学(人教版)三年级下册第5 课《面积》的教学为例。在教学这节课之前,学生对面积的概念及内容所知有限。而面积问题在小学中又属于常见但难度偏高的问题,因此,基础对于学生而言尤为重要。面积虽然只是数据,但它不可能单独存在,而必须依托于图形。为此,教师在面积这一知识点的教学中,可以采用数学中的数形结合方法。以其中的一道课堂练习题为例。
例题:已知一个长方形的周长为120 厘米,长比宽要长12 厘米,问该长方形的面积为多少平方厘米?
引导:通过简单的教学,学生已经熟知了长方形、正方形中面积与边长之间的关系,但本题中并未直接给出这个关系表达。为了方便学生计算,避免出现错误,宜采用数形结合的思维方法,可以先利用电子白板或传统的黑板工具构建一个符合题目要求的图形。如下图所示。
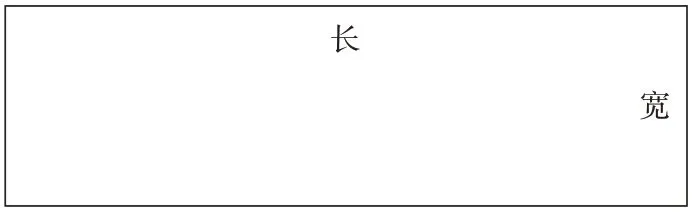
解析:由图形及题中所给出的条件可以得知,长+宽=60 厘米,长-宽=12 厘米,由此便可以直接计算出,长方形的长为36厘米,宽为24厘米。再代入面积公式s=长×宽,得出S=864平方厘米。
(2)样品滤筒溶液的制备[6]。将采样后的滤筒撕碎放入250mL锥形瓶中,加100mL水浸没,瓶口上放一玻璃漏斗于电炉或电热板上加热近沸,约30min后取下,冷却后将浸出液用中速定量滤纸滤入250mL容量瓶中,用20~30mL水洗涤锥形瓶及滤筒残渣3~4次,洗涤液并入容量瓶中,用pH试纸试验,加1.0或0.10mol/L氢氧化钠溶液中和至溶液pH7~9,再用水稀释至标线。
当然,在小学数学中,还存在许多其他的数学思维及解题方法。在以往的教学中,由于条件的限制,这些方法无法得到广泛的运用。教师必须紧跟时代的发展,在开展教学中主动引入新的工具,大胆进行尝试,这同样是STEM 教育理念的方向之一。
二、透析STEM教育理念,丰富教学内容
多门学科综合,多种技术共用,促进社会全面发展,个人水平全面提升,是STEM 教学的主要策略。此策略应用在教学中,就是要采用多种方式、结合不同学科,对知识点及其所包含的例题进行讲解,在丰富课堂内容的同时,强化学生的学习能力。在当前教育改革的背景下,这种教学模式有着独特而又神奇的作用。
(一)介绍知识背景,积累学生常识
在以往的教学模式中,教师常常一开始展开教学就讲解知识点或者以例题作为课堂的开头。这样的课堂设计虽然能在一定程度上给予学生思考联想的空间,但也容易导致学生根基虚浮,知识点基础知识掌握不够。STEM 教学策略要求教师的教学从根本出发,重点巩固学生对基础知识及知识背景的理解。为此,教师在课堂的设计上,可以以知识点的由来或在生活中的表现为开头。
例如在小学数学(人教版)六年级上册第5 课《圆》的课堂教学中,教师教学的第一步就可以介绍圆这种形状的由来及对其规律最早的发现。
在此之前,许多学生对圆往往会有这样的想法:“圆只是人们想象出来的图形,跟三角形、长方形等类似,都是由巧合情况被人所发现的。”人们接触到的最早的“圆”是太阳与月亮,在人的视角中,这两个天体呈现的形状就是标准的圆形。其实,早在数千年前,古人就已经能利用“圆”完成一些生活活动。例如陶器时代人们制作的陶器中,底边或开口有很大一部分就是呈圆形的;在春秋战国时期,搬运粮草或作战时使用的马车,其车轮同样也是圆形的。直到两千多年前,墨子提出了“圆”“一中同长”的概念模型,人们才对“圆”有了相对完整的认识。这一模型也为后世圆面积与周长的计算,提供了指引,也就是“圆”在教材中的知识内容。
对圆的由来及发展的具体讲述,既丰富了课堂氛围,提升了学生学习的兴趣,也强化了学生对知识的理解。从本质出发,更激起了学生探索生活中事物的渴望,为学生建立了像古人一般敢于探索、敢于发现的理念。这种理念正是社会所需要的,在此指引下,一些当前存在的问题,能够得到有效解决,社会发展的速度也能得到一定提升,这对应着STEM教育理念中人类社会持续发展的目标。
(二)引入视频资料,启发学生思路
随着信息化时代的持续发展,从网络中搜集资料已经不再困难。尤其是在教育领域中,有着大量的相关视频,值得教师在课堂中借鉴引用,以丰富课堂的内容。教师在选取视频资料的时候,可以重点关注这几类内容:科普类视频、高效数学方法讲解类视频以及名校名师讲堂等。在课堂中,播放这些优质视频,不仅能提升学生的学习兴趣,还能启发其思维,引导学生自主学习。
以小学数学(人教版)四年级下册第9 课《数学广角——鸡兔同笼》的教学为例。鸡兔同笼问题在小学中属于难度相对较高、需有一定推理能力才能解决的问题。同时,该问题解法多样,不同的解法步骤过程也不相同。然而,一种解法并不一定适用于所有学生,掌握多种解法也能在很大程度上启发学生的思维。为此,教师可以引入视频《鸡兔同笼问题解法集合》,让学生了解不同的解法,并选择其中一种或多种加以应用。例如在课堂中有这样一道例题:
鸡兔同笼,有头40 个,足116 只,问有鸡、兔各多少只?
针对这一问题,视频《鸡兔同笼解法集合》中给出了四种具体的解题方法,这里介绍其中的两种。
解法一:假设法,假设笼子里全为鸡。首先,学生必须清楚,题中给出的数据,头的数量实际上就是动物的数量。鸡、兔在本题中唯一的区别就是鸡只有两只足,而兔有四只。因此,当笼中全为鸡时,足的数量应该是40×2=80 只,而实际结果是116只,相差116-80=36 只。由于兔的足数比鸡多两只,因此可以得出兔的数量为36÷2=18只,鸡的数量为40-18=22只。
解法二:公式法,经过众多教师多年的经验综合,对鸡兔同笼问题建立了一套完整的公式体系,只要套用公式,便能有效解决问题。其公式为:总足数÷2-总头数=兔的数量,总头数-兔的数量=鸡的数量。代入题中就是:兔的数量=116÷2-40=18 只,鸡的数量=40-18=22 只。这种方法能较快解出答案,但存在一定的局限性,应对灵活的题目,则常常表现得束手无策。因此,该方法仅作为学生在没有思路时,备用的解题方案。
通过一个视频,学生认识了解决一类问题的多种方式,有基础认识部分,也有扩展提升部分。将此类视频引入课堂,既能丰富课堂内容,提升教学效率,也能适应不同学习情况学生发展的需要,符合STEM教育理念的策略要求。
三、应用STEM教育理念,激发学生潜能
STEM 教育理念的优势在于其灵活性与综合适应性,能够有效整合多种不同方向的内容,形成一个有机的整体。这种教育方式,对学生潜能的激发也能起到重要作用。
(一)学科串联,强化学生整合意识
学科的跨越性串联是STEM 教育理念的核心部分,该部分在小学数学中的集中表现是“将小学科学技术学习与数学学习之间相互关联”。科学技术与数学之间本就有着多重联系,科学的学习也必须建立在一定的数学基础之上。为此,教师能够较容易地将两者知识点结合进行讲解。
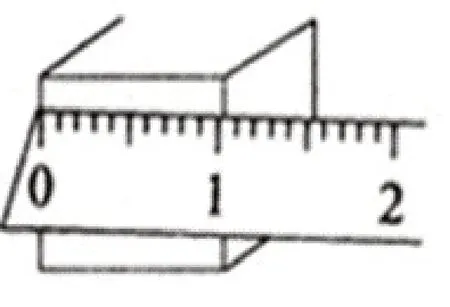
例如可以将小学数学(人教版)三年级上册第3课《测量》课堂教学与小学科学(人教版)第一册第四章第三节《尺的使用》进行串联整合。尺子是小学生测量物体的常用工具,而许多学生对于“尺”的规范使用并不清楚。而在小学科学的学习中,学生清楚了尺子在测量物体时的规范用法。以测量正方体的边长为例(如图所示),首先必须对齐零刻度线,其次在测量中,要使尺子与待测的面垂直,最后测出实际数值,并进行估读。以本次测量数值为例,正确的读数应为10.1毫米。
由此可见,学科的串联性对于教学的开展具有重要意义,其不仅能提升教学质效,还能建立一个良性的教学模式,帮助学生巩固所学知识内容,提升思维路径。
(二)齐头并进,促进学生全面发展
STEM 教育理念对学生的全面发展提出了很高的期望,希望学生能够借助STEM 教育的特殊模式,发挥长处,补齐短板,促进自身的全面发展。为此,在该理念的引导下,教师要着重关注学生在当前学习中存在的问题,及时进行纠正。
教学并不是单方向一味前进的过程,教师在开展教学时,也必须注意实时回顾。要以学生的学习情况为基础,做到齐头并进,使学生的学习成绩与认识水平稳步提升,满足STEM 教育理念在教育实践中的需要。
综上所述,STEM 教育理念作为教育体系改革下教学发展的主流思想,发挥着独到的作用。实施STEM 模式的教学,也是教育发展的必然趋势,教师要积极响应,主动接受。

