基于自适应网格划分的针织物仿真
胡新荣,汪 卓,刘军平,彭 涛,李 敏,李 丽
(武汉纺织大学, a.计算机与人工智能学院;b.纺织服装智能化湖北省工程研究中心;c.湖北省服装信息化工程技术研究中心,武汉 430200)
随着计算机性能的不断提升和计算机动画以及服装设计、虚拟现实等领域的发展,针织物的动态仿真成为了热门的研究领域之一。针织物的动态仿真大多数采用物理模型,而物理模型采用动力学方程求解的形式能够达到接近真实的仿真效果。物理模型的仿真方法又分为基于网格模型的仿真和基于纱线模型的仿真。
机织物一般由经纱与纬纱交错编织构成,在仿真中,其节点结构可以看作网格,如图1(a)所示,图1(b)中展示了其网格模型。将纱线的交点作为其中网格的顶端,纵向和横向的形变分别以纵向与横向的弹簧表示,而斜向的形变使用对角线上的弹簧表示[1]。为了表示材料的弯曲,可以跨节点加入弯曲弹簧,故基于网格并使用弹簧质点模型的仿真方法能够解决机织物的形变问题。而针织物一般由纱线的线圈按照一定的图案编织而成,编织图案的不同时,纱线在形成针脚时所体现的缠绕方式也各有区别。

图1 机织物模型及网格化表示
由于针法的不同,针织物在形变时所表现也不尽相同。比如弹力织物使用隔行正反针织法编织,而罗纹织物由一根纱线依次在正面和反面形成线圈纵行形成织物。这会导致弹力织物的边缘会产生卷曲现象,而罗纹织物会产生收缩,并呈现周期性的条纹。图2展示了弹力织物与罗纹织物编织的织物在静止时所表现出的差异。与此同时,由于针织物的编织方式不同,同一针织物在受力方面可能会表现出各向异性,即不同方向的受力也可能产生不同的形变效果。

图2 两种编织方式织物的形变
如果使用传统三角网格模型对图2中的两种针织物仿真,无法体现针织物纱线的编织信息,进而无法表征整个针织物在形变过程的物理特性。为了解决这个问题,一般的解决方法基于线圈模型,进行纱线级仿真。
线圈模型方面,传统的Pierce线圈模型由圆弧表示的针编弧、沉降弧和直线表示的圈柱组成,该方法结构简单却无法展示真实的形态。现有的方法一般使用样条曲线,并通过实际测量选取控制点。例如丛洪莲等[2]测量了纬编提花织物的线圈结构,并选取控制点建立模型,而张华等[3]也通过类似的方法建立了经编织物的模型。徐海燕等[4]使用了TexGen软件,采用了贝塞尔曲线插值的方法建立线圈模型,该方法建立的模型在曲线的表现与形态控制上更为方便。本文所使用的几何模型由设定的控制点经样条曲线插值而成。
针织物物理仿真研究中,Kaldor等[5]首次提出了纱线级别上进行针织物仿真的方法,但是由于碰撞检测每一步都需要计算节点间的距离,该方法处理节点接触的效率很低。随后Kaldor等[6]使用线性化接触模型与分块计算的方法简化了碰撞检测中的接触力计算过程,提高了整体仿真的效率。Yuksel等[7]提出了针织网格的数据结构,并以此为依据对织物进行仿真;该方法为自动化编织与交互式织物设计打下基础。Cirio等[8-9]为了提升效率,假设针脚间持续接触,避免了接触节点间的碰撞检测,在不损失精度的同时提升了仿真的效率。Jiang等[10]在Cirio的工作的基础上,引入物质点法,使仿真效果更加真实。Fei等[11]在该方法的基础上研究了基于纱线模型的织物与水接触所产生的形变特征。
纱线级织物仿真,首先将纱线模型进行离散化处理,在每个针脚处形成接触节点与纱线之间的弹力模型。图3(a)、图3(b)是对一个简单的针脚离散化的纱线模型。在图3(b)中,互相缠绕的纱线被简化为直线,而接触处的圆圈表示接触节点。对于更复杂的针脚,如加针,其离散化表示也更为复杂,如图3(c)、图3(d)所示。对这些接触节点进行受力分析,列出关于能量的方程为纱线级仿真常用的求解形式。由于机织物也由纱线纺织而成,该方法的纱线模型经过改动后一般也可以用于机织物的仿真。纱线仿真虽然能真实地表现针织物的变形特征,但是由于建模的复杂性,在模型节点较多,或分辨率较高时,其仿真速度一般都很慢。

图3 针织物的3d模型及离散化表示
另一些研究使用混合网格与纱线的模型进行织物的仿真。Narain等[12]提出了在动态网格划分技术在织物仿真上的应用,Casafranca等[13]将两种仿真方法混合使用,在变形较明显处使用纱线仿真,其他地方使用网格仿真并引入平滑因子消除两者结果之间的误差,但纱线仿真区域需要在仿真前手动指定。Leaf等[14]以织物图案的周期性对仿真进行探讨。Sperl等[15-16]提出了均质化纱线仿真的方法,该方法在微观层面使用周期性的纱线模型进行纱线级别的仿真,用来度量不同形变下该纱线模型的形变特征,将其结果映射到网格仿真的宏观织物模型上,得到最终的结果。李双双等[17]提出自适应网格的方法进行织物仿真,使用到了边缘曲率检测的方法,但该方法的划分依据完全依靠几何信息,对真实的物理形变不够敏感,且不适用于针织物。
综上所述,目前的针织物仿真技术由于建模复杂,其仿真效果比起网格模型而言,更加接近物理真实,但由于其方程求解过程复杂,仿真过程非常慢,难以在短时间内得到一个比较准确的效果。
由于针织物大多数都使用某种特定的图案进行编织,只对周期性的图案进行仿真,避免重复计算加快针织物的仿真速度,而该特性同样可以结合传统的网格仿真方法。同时,引入自适应网格划分技术可以提高网格仿真的效率。结合以上几种技术的特性,本文将提出一种基于自适应网格的针织物仿真方法。
1 网格化与动态划分
在织物形变过程中,有些接触面比较平整,使其形变幅度较小;而有些接触面比较窄,或者凹凸不平,容易产生较大的形变。为了在分辨率较低的初始网格模型在形变细节上也能得到较好的仿真效果,以及提高仿真的效率,将采用自适应网格划分技术,同时为了结合纱线仿真,将对于针织物模型做一些特别处理,其中形变表示方法与约束参考Narain等[12]的论述。
1.1 网格表示
如图4所示,将初始服装网格的UV坐标为基础,生成背景网格。和服装网格模型不同,周期性纱线图案一般为正方形,如图4(a),所以背景网格也是正方形,网格尺寸为周期图案的尺寸。图4(a)所示的网格大小为1×1,图4(b)的服装模型的腰宽为5,网格密度为6.25。然后用周期性的纱线图案去铺满整个背景网格,随后去掉服装网格之外的顶点与纱线段,即可生成初始的纱线模型与网格的对应关系。

图4 建立初始网格与纱线图案对应关系[16]
为了得到不同尺寸的服装纱线模型,网格密度可以结合实际需求进行调整。在后续实验中,将统一使用图4所示的网格密度与尺寸。
在初始模型生成后,每个三角网格与其范围内的纱线一一对应,网格在后续映射步骤中对应的是纱线模型的中位面,中位面顶点的位置决定形变的宏观效果,而其网格对应的纱线片段的形变决定其形变的细节。图5是周期性纱线模型与其对应三角网格在形变中经历的变换过程。自适应划分后,其网格切分与组合也会使其对应的纱线模型片段切分或组合。
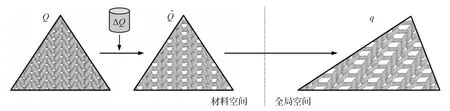
图5 网格到纱线模型映射过程[15]
1.2 形变描述
本节将描述网格模型与纱线模型上,形变的表示方法。
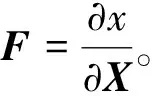
宏观量与微观量之间的对应关系如下:
(1)
(2)
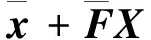
(3)
其对应的关系如图6所示。

图6 网格形变描述

1.3 周期约束
区别于普通的网格仿真,为了整体模型纱线的连贯性,周期性的纱线模型在映射到网格后,必须要加上纱线的周期性约束。在视觉效果上,相邻两个网格之间所对应的纱线头不能随意断开,也不能出现不连贯的弯曲。

(4)

(5)
同样地,该式也可记作:
(6)
式中:R为旋转矩阵,由于旋转矩阵是正交矩阵,所以R-1=RT。为了使纱线扭曲符合周期性约束,约束区域Ω内正反向扭曲相抵,即θ+=θ-。这些约束条件会在进行物理仿真时减少其过程中产生的计算误差。
1.4 自适应划分
由于仿真过程的总体形变效果是由网格模型产生的,在建立网格与纱线模型的对应关系后,需要对网格模型进行仿真。为了提高仿真的效率,并保持网格模型处理整体形变时的准确性,在仿真过程的每一次迭代之后,需要根据形变的大小、速度、碰撞点的距离等参数进行自适应网格划分。
总体而言,自适应划分的操作对象是网格模型的边,以上一步所得到的网格模型为基础,首先需要对网格进行细分,为了保证网格边缘与形变特征,都需要对网格边进行翻转。为了防止网格的无限细分,然后网格然后进行粗化。网格粗化后也要对部分边进行翻转操作。根据Narain等[12]的论述,为了准确地细分网格,首先需要计算张量场M,该场代表了网格中每条边被允许的最大长度。当一条边的s>1时,需要对该边进行切分。记Xij=Xi-Xj,则两个顶点i和j的距离s与M之间的关系可以定义为式:
(7)

(8)
(9)
(10)
(11)
(12)

(13)
(14)
(15)
然后令Λ=diag(λ1,λ2),最后得到M=QΛQT。
如图7所示,对边AC进行切分是加入AC的中点P,由于AC被三角形ABC和ACD公用,所以需要连接PB和PD。同时将速度、张量场M等参数插值给点P。对AC进行翻转操作则是去掉AC连接BD。粗化AC则是去掉点A,并将原来与A连接的边改为与C连接。粗化过程中边是有向的,也就是说粗化CA是去掉点C再将与A相连的边连向C。

图7 对边AC网格划分操作
当边AB去掉点A引入的新边不需要重新划分,且去掉该点不会影响网格UV图的外形时,可以对AB进行粗化操作。当一条边AC的τ<1时需要将该边翻转至BD。其中τ定义为式:
(16)
整个自适应划分的流程如图8所示。

图8 自适应网格划分流程
2 物理仿真
仿真的流程如图9所示。下文将分别介绍其中的细节。
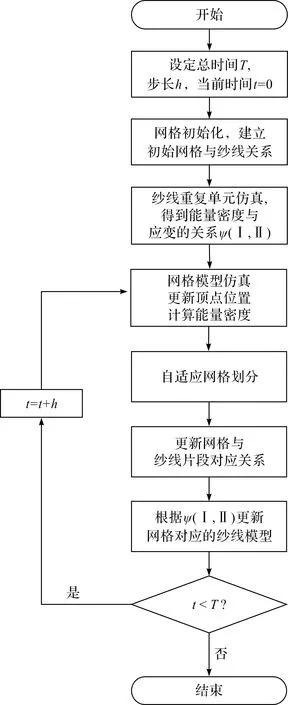
图9 针织物仿真流程
2.1 纱线仿真流程
由于直接对整个纱线模型进行纱线仿真很慢,对需要进行仿真的材料,文中只对其周期性的重复单元进行纱线仿真。周期性模型输入包含了纱线材料的参数,以及编织纱线的节点坐标,使用三阶B样条曲线插值可以得到该周期模型的图案。
纱线仿真所使用的模型是Bergou等[18]提出的离散弹性绳结模型。在仿真过程中,为了更加真实地体现出纱线模型边缘的形变,需要通过周期模型的一小部分,经过平移、旋转操作在其边缘稍做扩展。
接着分析纱线的能量:
(17)
式中:Es为纱线的拉伸能量,Eb为弯曲能量,Et为扭曲能量,Ec为每个周期模型间的碰撞能。能量对坐标x求导,就可以得到纱线的受力情况。

(18)
式中:|Γ|为中位面Ω的面积。

(19)
2.2 网格仿真流程
对于织物的宏观形变可以使用基于三角网格的仿真来解决。这种仿真使用弹簧质点模型,首先对该模型进行受力分析,确定求解的微分方程,然后选取合适的时间步长进行求解。
求解物理仿真求解微分方程的方式可以分为显式时间积分与隐式时间积分。显式时间积分法一般采用较小的时间步长,否则容易产生数值波动,使得视觉上会出现抖动等现象,但时间步长小的仿真效率很低。所以织物仿真一般使用隐式时间积分[20]。其优势在于可以配合更大的时间步长,并且可以在求解过程中获得更稳定的物理仿真效果,劣势则是增加了求解步骤中的复杂性。
求解微分方程前,首先计算每个网格三角形面片的形变梯度FΔ,公式如下[14]:
(20)
式中:φi与ξi表示材料空间和全局空间下,网格中第i个顶点的坐标。
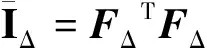
(21)
式中:θi为网格与第i个相邻网格平面之间的夹角,A为三角网格面片的面积,li为第i条边的边长,ti是长为li的三角网格面的法向量。
2.3 纱线模型生成
在自适应划分之后,整个网格发生了变化,但纱线模型只是跟着网格模型发生形变,此时,需要重新建立网格与纱线片段的对应关系。通过网格边切割纱线模型的办法即可做到。


最终得到整体形变后的纱线模型。
对于网格仿真后输出的网格模型,采用上述方法即可得到对应的纱线模型。
3 实验结果
本实验代码使用C++语言以及OpenGL框架编写,运行于Intel Corei7-9700八核处理器、NvidiaGTX 1060 6GB显卡与Ubuntu 20.04操作系统上。下面将从织物的悬垂效果与着装两个实验来分析使用自适应网格仿真的效果。
3.1 悬垂实验
为了表现不同织物形变的特点,实验使用了弹力织物、罗纹织物与席纹织物3种不同的织物模型作为输入,分别观察它们在与球碰撞后的悬垂效果,仿真过程中织物的两个顶点与球的位置是固定的。实验使用的初始网格模型含有2625个顶点,5168个网格,总体的仿真时长为2 s,每帧的时间步长为1/60 s,但仿真在0.5 s时,整体开始趋于收敛。
图10是仿真进行至t=0.5 s时,弹力织物、罗纹织物和席纹织物分别在横列与纵列与球碰撞产生的形变效果。在弹力织物与罗纹织物中,两种悬垂方式的形变效果差异较大,而席纹织物由于其横列与纵列的针法相同,其悬垂效果无明显区别。而同一悬垂方向下,3种不同的织物也显示出了各自不同的形变效果。

图10 t=0.5 s时不同编织方式下悬垂效果
图11显示了罗纹织物横向悬垂在实验的仿真过程中在3个不同时刻网格划分情况。可以看出在形变过程中固定点和碰撞部分及中间部分网格进行了细分。
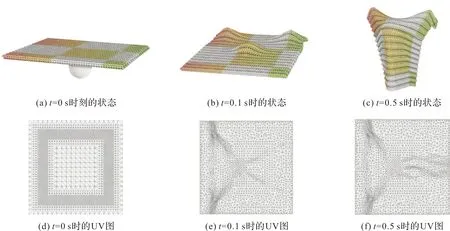
图11 自适应网格划分效果
3.2 着装实验
为了计算使用自适应网格划分仿真的时间效率提升幅度,以及观察低分辨率网格模型输入下的形变效果,实验对于5种不同的针织模型结合人体动画进行服装仿真,原始服装网格使用了3303个顶点与6514个网格。表1为几种材料的参数。

表1 实验用纱线图案的参数
预设动画的时长为20 s,时间步长为1/60 s,即动画总共有1200帧,该动画只包含人体模型的运动过程。而仿真过程中,需要逐帧计算服装模型的形变以及与人体之间的碰撞,通过迭代使得某一帧的服装模型稳定后,将该帧的服装模型和下一帧的人体模型输入,再进行下一帧的仿真过程,直到动画对应的仿真过程全部结束,整个仿真过程完成。动画每一帧的形变计算所耗费的时间总和即仿真的总时长。最后,将使用自适应划分仿真所减少的耗时与使用原始网格的仿真耗时相除,得到时间效率提升的百分比。
实验结果表明,由于仿真过程与模型的顶点数相关,且自适应划分方法相比原始网格减少了20%~30%的顶点与网格数,在仿真计算过程中减少了计算量,使得使自适应网格划分比起直接使用原始网格在时间效率上有23%~40%左右的提升,其最大提升为39.7%,结果见表2。其中罗纹织物比起其他针法,由于收敛较慢使用了2倍左右的仿真时间。

表2 仿真结果对比
形变效果如图12所示。使用动态网格化划分与使用原始网格的实验效果对比。在第300帧下,使用动态网格划分的方法效果如图12(a)所示,而使用原始网格的情况下效果如图12(b)所示。可以看出图12(a)相比图12(b)在较大形变展现出了更加接近真实的效果,而图12(b)由于其网格过于稀疏,其仿真效果比较图12(a)产生了过多的褶皱。
为了得到两个模型间的形变差异分布,实验计算两个网格顶点之间的Hausdorff距离[22],即找到图12(b)中每个顶点在图12(a)中最近的顶点及其距离,最后将该距离映射到图12(a)的网格上,其热力图如图12(c)所示。图中颜色越深代表其形变差异越大。可以看到在形变较大的位置,如图12(c)用虚线框圈出的位置存在明显差异。

图12 使用自适应网格与原始网格的效果对比
4 结 论
由于虚拟现实及动画制作、针织自动化生产等一系列日益增长的需求,针织物仿真成为了计算机物理仿真的研究重点。为了解决针织物仿真使用传统网格模型细节效果不够真实以及纱线模型仿真建模复杂导致仿真效率低下的问题,本文提出了一种结合自适应网格与纱线仿真的针织物仿真方法,在使用网格模型进行宏观效果的仿真的同时使用纱线最小重复单元在不同形变下的映射来改进微观效果,该方法体现不同的针织物在形变细节上的特点,并且在时间效率上得到了时间效率上23%~40%的提升。但该方法的纱线模型在设计上只能针对周期性纱线编织的织物,没有考虑非周期性的或者多个重复单元的模型,故不能直接使用此方法表示与仿真更加复杂的织物模型。

