二维闸门流动特性的试验和数值研究
池苗苗
(塔里木河流域干流管理局,新疆 库尔勒 841000)
水闸是明渠中测量水位和控制流量的常用方法,而且它在捕获漂浮物方面也发挥重要作用[1]。工程研究通常采用经验公式,该公式源自收缩系数Cc或流量系数Cd[2]。然而,水下闸门也可能在大开度(a>0.5)下运行,甚至可能完全打开,此时将导致水位-流量关系不连续[3]。在这种情况下,可以应用能量动量平衡(EMB),当考虑亚临界流时,Cc会发生剧烈变化,当闸门边缘仅接触自由表面时,几乎不会产生收缩。EMB是一种常用计算流量的方法,他需要修正系数来调节Cc的值。为此,需要通过研究流动形态来量化由黏度和湍流引起的水头损失,并评估动量和能量系数[4]。除此之外,确定流动形态也有助于研究闸门上游污染情况。通过实验研究、势流解和数值模拟,研究学者对自由流型给予了极大关注。随着计算机技术、两相模型和湍流模型的发展[5-6],计算流体力学工具已成为分析流动形态的有效方法,同时可以用于补充实验工作[7]。龙多[8]研究了闸门自由流情况下的雷诺平均Navier-Stokes(RANS)方程,重点模拟了压力场和网格对数值结果有效性的影响。相比之下,淹没流的研究较少。而且在水闸系统大开度时的流态变化研究仍是不充分,也没有准确描述闸门射流的流动特性[9-10]。
本文的目的是借助数值模拟方法研究闸门水流相关特性,以改进大开度水下水闸的流量计算。为了实现这一目标,进行大量速度测量全面描述不同方案的流量,同时还考虑了不同湍流模型的模拟精度。这些模拟针对不同下游条件和开度的情况进行了验证。最后还讨论了标准RANS模拟方法在此类水工结构中的有效性。
1 研究方法
1.1 实验设置
实验水槽宽30 cm,高50 cm,长8 m,由玻璃墙和底部钢板组成。水闸位于水槽的中间。流量通过向水槽供水的进口管上的阀门进行调节,并通过超声波流量计在进口管上进行测量。下游深度由水槽下游端的可调堰调节。闸门由有机玻璃制成,边缘锋利,厚度为5 mm。闸门开度从2~24 cm不等,精度为0.2 mm。自由流的上游深度约为0.2 m,淹没流的上游深度约为0.3 m。使用Nortek声学多普勒测速仪测量速度。采样率为25 Hz。选择样本体积和传输长度是为了确保测量条件准确性,因此信噪比大于20,总计数大于70。传感器垂直安装在直径为1 cm的圆柱形杆上,可在垂直方向上达到0.5 mm的精度,在纵向上达到2 mm的精度。对于每个点,在40 s内记录了三个速度分量。并借此获得平均速度和湍流强度。通过分析和平均瞬时数据计算湍流特性。由于能谱中几乎没有噪声,因此无须进行校正。
1.2 模型设置
模拟了27种方案,见表1。用FLUENT软件求解非稳态下的RANS方程,压力场计算采用半隐式压力关联方程法(SIMPLE)算法,用二阶格式离散其他方程。为了追踪自由表面,使用了部分流体体积模型,该模型采用VOF(流体体积)公式,但与VOF不同的是考虑了气体部分。整个领域考虑了两个相(水和空气),流体的性质随域中每个相的体积分数改变,然后用体积分数平均值求解RANS和连续性方程,对模拟的自由表面位置进行插值。湍流动能(k)由纵向和垂直方向上的速度定义,见式(1):
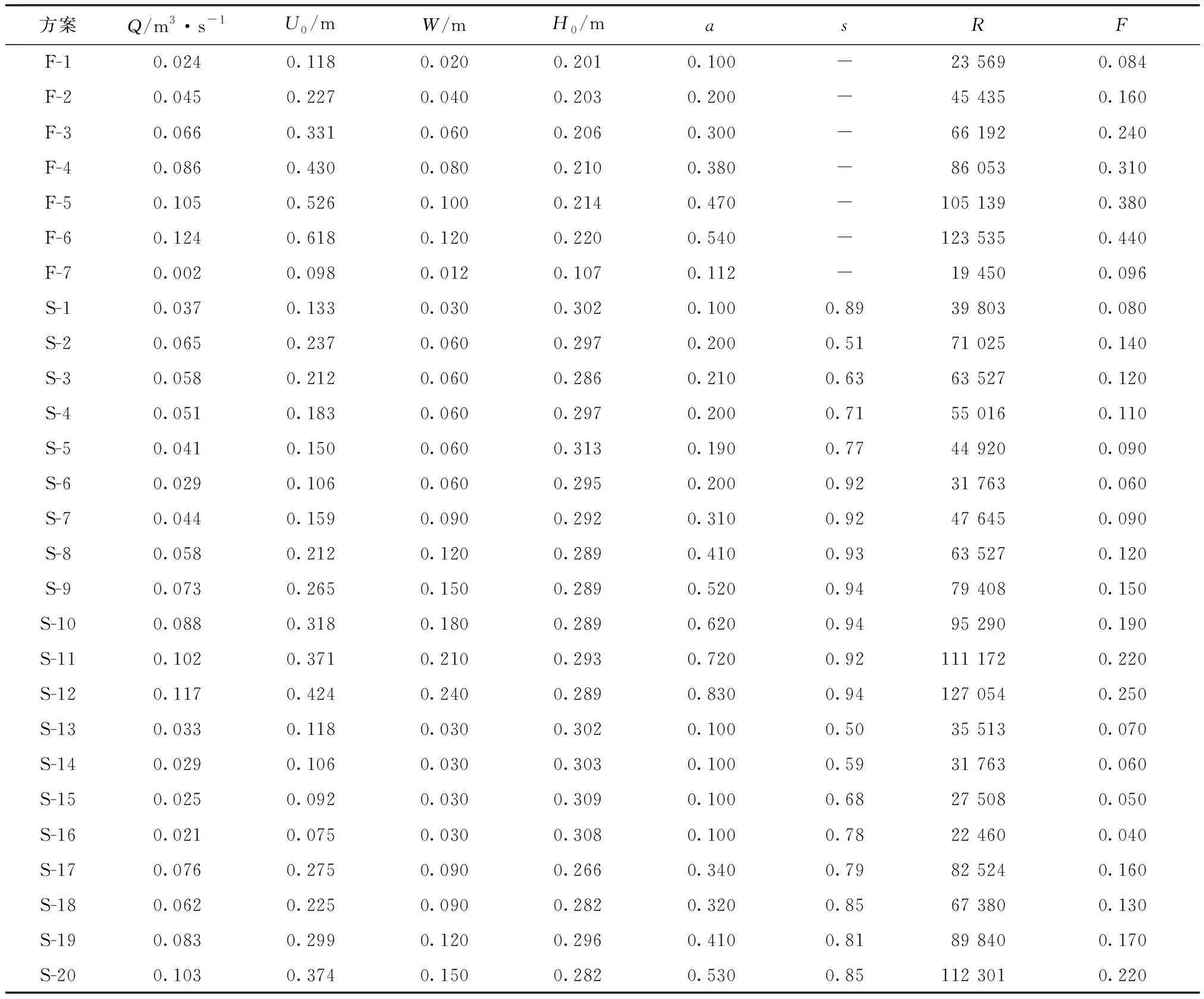
表1 方案设置
(1)
式中:k为湍流动能,m2/s2;u和v分别为纵向和垂直方向的速度,m/s。
由于k-ε模型易于收敛并精度较高,常用于工程中计算水跃。在本研究中,考虑到计算量且要适用于应变流,RNGk-ε模型作为模拟的湍流模型。还使用了一种各向异性模型用于对比分析,即雷诺应力模型(RSM),该模型可以更好地描述分离点附近的二维流动。所有模型均使用FLUENT中可用的标准值进行参数化,并分析了湍流模型对速度剖面的影响。
1.3 计算网格
使用GAMBIT软件生成2D结构化网格。自由流的域尺寸为4.0 m×0.4 m,淹没流的域尺寸为6.0 m×0.6 m。闸门位于3.0 m处,在入口边界的下游,作为水平横坐标x的原点。网格在边界(底部和水闸)和自由表面附近进行了细化。同时为了避免单元扁平,两个连续单元之间的尺寸比要求<1.5。对于自由流动,网格需细化直到对Cc的影响变得可以忽略不计(<0.5%),速度最大误差小于2.0%。并要求12 图1 网格局部 边界条件如图2所示。水和空气在入口处以两种速度条件分别注入。结果显示对空气速度不敏感,空气速度最终被设置为零。给出了进水速度分布的幂律曲线,如式(2): 图2 计算域参数和边界条件 (2) RANS模拟与试验结果对比如图3和图4所示。除了靠近闸门的表面(-1 图3 淹没流的纵向速度剖面 图4 闸门上游x=-0.1 m处自由流中三个开度的纵向速度剖面 在淹没流中,两个模型都再现了射流区的纵向速度剖面,但最大速度存在一定程度的高估。这一差异(小于5%)可能与河床粗糙度有关,河床粗糙度并非严格为零,以及流量估计可能存在的误差。根据速度剖面计算收缩流yc(图3)。他们与yc的实验值一致,估计精度约为1 cm,这归因于测量速度以1 cm或2 cm的间隔测量。两种模型的收缩段均位于1 图5 淹没流的湍动能剖面 总水头损失接近(1-s)H0,而水跃前的水头损失(用ΔH表示)是通过上游段(x=-0.4 m)和收缩段之间的压力、速度和k积分计算的。 在自由流中,ΔH主要归因于摩擦底层产生的损失。流动对雷诺数的依赖关系与底层的边界层有关,如图6(a)所示当W<0.06 m时,尺度效应显著,以至于ΔH/H0>0.02。在淹没条件下,摩擦底层和混合层都参与了能量耗散。ΔH/H0的值表明,在收缩段之前(如图6(b)所示),部分能量(约25%)已经发生耗散,例如在湍流边界层和射流上方的混合区域。当a=0.4 m。虽然估计值接近于大淹没,但在小淹没时出现显著差异。 图6 上游和收缩段之间的水头损失(ΔH) 本文对闸门流动形态和水力参数进行了二维的数值模拟研究,并得出以下结论: (1)湍流模型的选择对模拟结果有着重要影响,因为标准k-ε和k-ω模型在很大程度上高估了收缩流的厚度。 (2)利用RSM和RNGk-ε,可以精确地计算速度剖面。但在自由流中,用k-ε模拟的Cc比用RSM模拟的Cc高约17%,RSM与实验值更加接近。 (3)当W<0.06 m时尺度效应显著,以至于ΔH/H0>0.02。在淹没条件下,摩擦底层和混合层都参与了能量耗散。对于闸门开度较大的淹没流,不应在自由流(约0.61)中考虑Cc。
1.4 边界条件
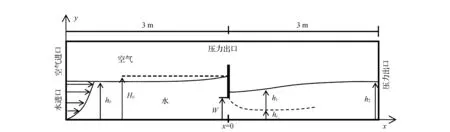
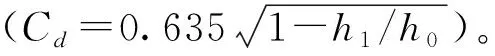
2 结果和讨论
2.1 湍流模型对比
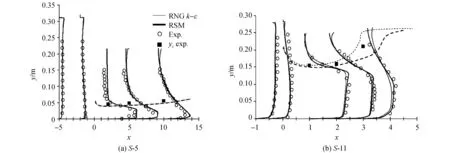
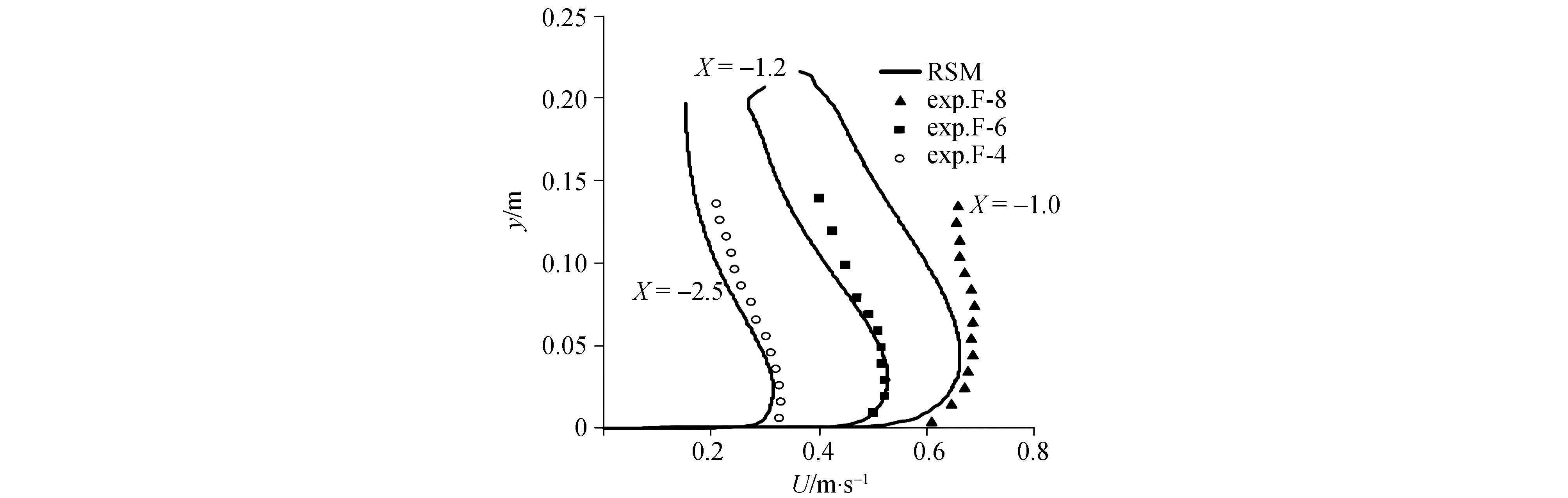
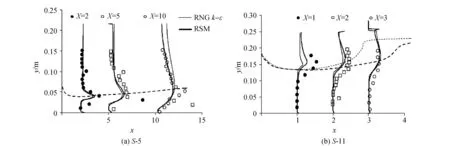
2.2 水头损失
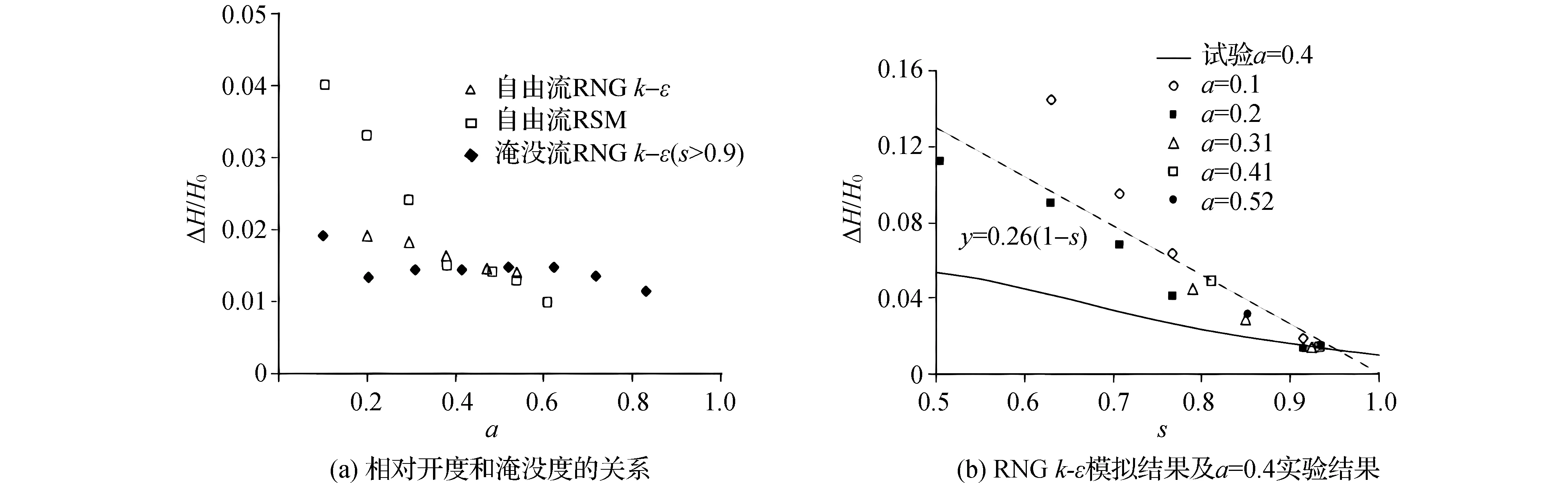
3 结 论

