石墨抗热震性能评价方法研究

匡格平 林 川 王 群 张雪峰 徐秋发

（北京宇航系统工程研究所）

航天飞行器底部发动机突然点火的瞬间，会产生高温燃气冲击，这种剧烈的热震作用会使附近结构尚未出现烧蚀就发生碎裂，进而导致结构失效，因此，热防护结构抗热震性是飞行成败的关键。在飞行器结构设计中，一般采用具有良好抗热震性的特种石墨为防热结构，影响石墨抗热震性因素很多，如物理性能、微观结构、结构尺寸等，一般都采用发动机试车的方法定性地判别抗热震性的好坏，不易通过计算方法来精确求得。

本研究试图采用工程计算、有限元分析相结合的方法完善石墨抗热震性能表达式，识别材料性能中对抗热震因子敏感的参数，对不同石墨制品的抗热震性能进行综合评价，并与发动机试车结果进行对比，为后续特种石墨研制提供参考依据。

1 抗热震性定义

所谓抗震性或抗热冲击性即材料抵抗急热急冷的能力，根据定义［1］，加热或冷却速度大于93 ℃/h 叫热冲击。现代工业中许多机械零件或构件是在热冲击条件下工作的，最典型的例子则是飞行器尾部底端防热结构，局部温升能达到1 800 ℃/s 以上。热冲击条件下产生的热应力是动态，其作用效果比静态应力大得多，往往足以使韧性材料产生脆性破坏。热冲击条件下，结构件变形断裂是失效的主要形式，这是热冲击裂纹扩展所引起的，正确地评价石墨材材的抗热震性能，揭示石墨微观结构对热冲击裂纹扩展方式的影响，改善和提高材料的抗热震性能，已成为特种石墨研制应用亟待解决的问题。

2 抗热震性公式推导

在热震过程中，材料产生的热应力

式中，ɑ 为热膨胀系数，℃-1；E 为弹性模量，MPa；u 为泊松比；ΔT为温差，℃。

由式（1）可以看出，在热震过程中，石墨受到的热应力与石墨的弹性模量、热膨胀系数成正比。

通常，抗热震性可用热应力阻值R 表示，它是材料某些力学和热学性质的复合函数，与热应力呈反比关系［2］

式中，ɑ 为热膨胀系数，℃-1；E 为弹性模量，MPa；u 为泊松比；S为抗拉强度，MPa。

该公式仅适用于高速给热的大面积而低导热率的平板试样，对处于飞行器发动机底部热流的石墨试件来说，该公式没有考虑热学参数对局部温度传递的影响，因此对其进行修正，加入热导率K，表达式［2］为

式中，K为热导率，W/（m·K）。

根据文献［3］记载的石墨材料性能（表1），热试车试验结果见表2，按式（3）计算，KS-8高强石墨热应力阻值R比T704、T705石墨低得多，但在实际SRM点火试验考核中，KS-8 石墨抗热震性能却明显优于T704、T705石墨。切应变。

?

?

在以往型号研制中，在热应力阻值相差不大的情况下，还不能靠数据完善表征抗热震性能的优劣，需要进一步用发动机试验进行实际考核。

上述热应力阻值计算结果与试验结果不符的原因在于式（3）没有考虑石墨的微观结构（图1），因特殊的热震环境，特种石墨一般采用中粗颗粒，故形成的孔隙可吸收较大的热应变，使热应力松弛，减轻材料破裂的机理，这种方法不但在石墨材料中适用，而且在陶瓷材料、金属粉末冶金材料中均得到验证。

由于石墨的热震破坏是沿微观孔隙扩展的剪切破坏，根据诺顿剪切理论，热震因子［4］

式中，ɑ 为热膨胀系数，℃-1；K 为热导率，W/（m·K）；ρ为体积密度，g/cm3；c 为比热容，J/（g·℃）；φ 为最大剪

孔隙对石墨抗热震性能影响很大，最大剪切应变跟气孔形状及数量息息相关，根据断裂理论，脆性材料在断裂前没有显著的非弹性变形，破坏是突然性的。当材料受应力负载时，在其平均应力还未达到材料的理论断裂强度时，在不规则气孔的曲率最大尖点区域却已产生应力集中，局部应力达到或超过断裂应力，于是裂纹扩展，当局部区域的气孔达到一定数量，裂纹持续扩展，最终断裂。因此，本研究提炼出气孔的曲率半径R 和孔隙率h 作为修正最大剪切应变φ 的2 个关键影响因子。在石墨生产工艺中，由于曲率半径无法直接测量，可采用磨粉工序中的细粉粒度L表征气孔孔径大小，石墨颗粒的粒度越大，形成的石墨产品气孔孔径也相对越大，同时考虑产品宏观尺寸对结构热震性的影响，将引入细粉粒度L与产品的当量厚度d的无量纲比值L/d，而孔隙率

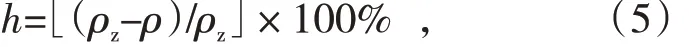
式中，ρz为真密度，g/cm3，无孔石墨的理论密度（真密度）为2.26 g/cm3；ρ为体积密度，g/cm3。

根据最大剪应力理论，最大剪切应变φ又可以表示为

式中，ɛ为拉伸断裂应变。

综上所述，热震因子

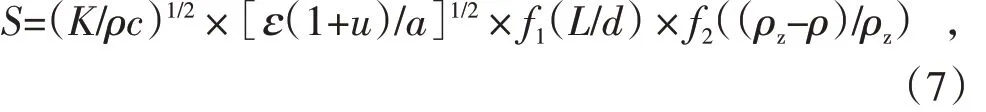
式中，f1、f2的函数形式可根据具体试验数据拟合得出。

本研究采用Exfm 裂纹扩展计算方法，利用abaqus软件建立50 mm×50 mm 的平板Maxps损伤有限元模型，在上面制出一定孔径的初始缺陷，有限元模型见图2，通过预定温度场的方式给定热载荷，以裂纹扩展长度表征热震因子，通过材料参数的调整，根据模拟结果计算最终函数形式。

分别模拟密度ρ=1.2、1.7、2.2 g/cm3，其余参数相同，得到的裂纹扩展长度见图3、图4、图5。

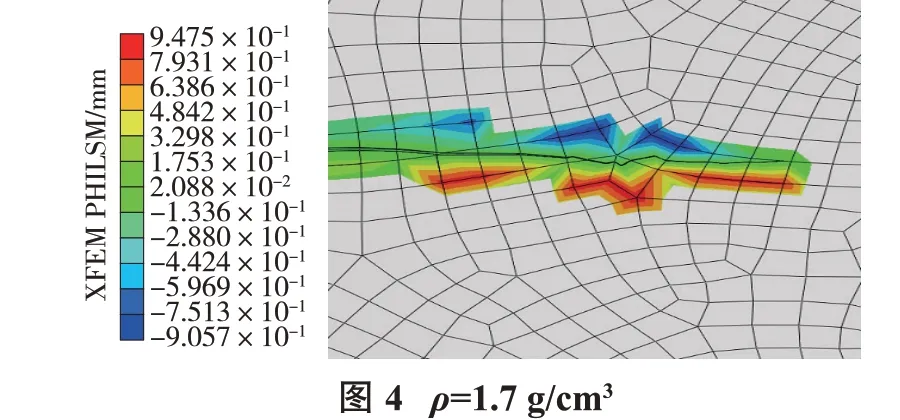
将上述结果代入式（7），拟合求得f2=-0.134 7h2+0.009 4h+0.249。

分别模拟石墨平板试件中心圆孔R=5、10、15 mm时，其余参数不变，同一时刻裂纹长度分别为5.43、8.95、11.75 mm，见图6。

将模拟结果代入式（7），拟合求得f1=0.570 6 R0.705。

同时，材料的热扩散系数λ=K/（ρc），mm2/s。

因此，优化后的热震因子

3 石墨抗热震性能评价及考核验证

为更好地评价石墨材料抗热震性，本研究用同样的工艺生产了2 批次M/Y 共4 种石墨，其中01 批2种石墨分别以M1、Y1表示，02批2种石墨分别以M2、Y2 表示，每种石墨取轴、径各30 根试棒测试材料性能，在泊松比u 取0.2，试件当量厚度d 取1 μm，不同性能情况下的热震因子S见表3。

从表3 可以看出，除M2 轴向热扩散系数异常偏低导致轴向热震因子计算结果低之外，M2、Y2 的热震因子明显高于M1、Y1，计算结果表明，M2、Y2 石墨具有更好的抗热震性能。

?

为验证上述结果，本研究取4种石墨M1、Y1、M2、Y2 各2 块，进行全尺寸发动机地面点火试验，发动机选取实际工况型号，试车燃气流温度在1～2 s 内升至1 800 ℃，持续60 s，试车后石墨热震结果见表4。

?

从表4可以看出，M2、Y2石墨的抗热震性能优于M1、Y1 石墨，验证了修正热震因子理论公式的工程适用性。

M2、Y2 石墨相比 M1、Y1 石墨材料的细粉粒度提升8%～10%，制成的石墨材料气孔孔径更大，增加了石墨制品的缓冲（吸收）热应力能力，该因素对于抗热震性作用非常重要，在以往的工程计算中往往被抗折强度等机械性能更高，但电阻率和热膨胀系数等热学性能变差了。因此，可以得出3个工艺机械性能由高到低的依次为二浸三焙二次沥青浸渍、二浸三焙二次树脂浸渍、一浸二焙；3 个工艺热学性能依次为一浸二焙、二浸三焙二次树脂浸渍、二浸三焙二次沥青浸渍。忽视，导致理论计算与试验结果不一致。

本试验中M1 与Y1 虽然都出现了裂纹，但M1 试件是贯穿裂纹，Y1 试件是细小裂纹，M1 的热震因子稍高于Y1，可能是内部气孔形状及分布决定了试验结果差异，优化抗热震因子将内部气孔当作理想圆孔计算，实际产品中，气孔形状会变成椭圆，或者尖点，造成曲率有很大差异，影响抵抗裂纹扩展能力。

4 结 论

研究采用工程计算、有限元分析相结合的方法对石墨抗热震因子进行了修正，通过识别敏感参数，将孔隙率及气孔曲率半径引入公式，对01、02 批M/Y的抗热震性能进行了定量分析，并通过地面发动机点火试验，验证了02 批M/Y 石墨抗热震性能优于01批M/Y 石墨。修正后的热震因子在一定程度可用于指导特种石墨研制。