分析城市轨道交通干式变压器经济可靠运行策略
王
(海南金盘智能科技股份有限公司)
0 引言
近年,我国城轨交通系统不断完善,明显减轻交通堵塞现象。有统计资料记载,到2019年年底,大陆地区有40个城市开通了轨道交通,线路总长6730.27km。供电系统的运行状态关系着城轨交通是否能实现平稳发展。变压器是供电系统的核心构成,应积极做好运行管理及故障诊断、处理工作,这是城轨交通安稳运行的重要前提。关于变压器可靠性模型建立问题,业内学者陆续运用各种定量或定性分析法,结合设备既往故障或运行数据做出综合性测评,并且研究内容还逐渐拓展到预测运转状态、剩余寿命等。做好故障诊断工作有益于减少设备运维费用,增强经济运营能力。
1 干式变压器的介绍
铁心、绕组、外壳及其他组件等是干式变压器的主要构成。铁心基本结构通常有两种,即心式与壳式,心式变压器铁心呈垂直状态,绕组被套装于铁心柱之上。壳式变压器把由硅钢片制成的铁心插进扁平形的绕组中,木楔塞紧铁心片和绕组的空隙,所以机械强度相对较高。在我国,全面考量费用投入、制造难易程度等因素,通常运用芯式变压器。关于绕组相关问题,多运用箔式结构以提升机械强度及冷却性能。另外,也不能忽视其内外部的绝缘结构,多选用IP20 或IP23作为变压器的防护外壳,后者能较好地阻止大型异物或小型动物进入,但散热性能偏差。
干式变压器的耐热性非常好,通常能抵达F级或H级,部分甚至能实现C级。这类变压器通常运用风冷,包括自然或强迫风冷,在强迫风冷工况下,变压器的过负载及抗短路能力均很强。
2 变压器可靠性建模
2.1 遵循威布尔分布规律的MTBF运算公式
MTBF即设备邻近两次故障之间的平均持续时间(tMTBF),运算公式[1]:

式中,ti表示变压器第i次发生故障的间隔时间;N即故障发生总频次。
综合精准性与现实状况,工程内所用概率分布平均值t"MTBF代替tMTBF。普遍认为电气设备的故障间隔时间遵从威布尔分布规律,取双参数威布尔分布作为平均故障时间(t)的分布类型,涉及的概率密度函数:

式中,α、β分别表示比例、形状参数。
对上式求积分有:
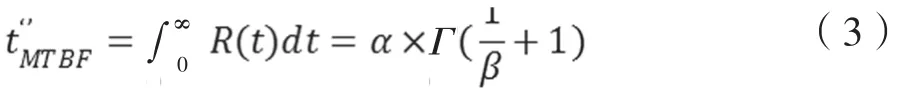
式中,Γ、R(t)分别是伽马、可靠度函数。
2.2 基于家族故障数据的参数估测
研究变压器的家族付账时,能获得两类数据,其一是故障间隔时间,其二是变压器最后一次故障发生时距离其推出运转时的时长,被叫做截尾时间。截尾时间阐明下一次故障间隔时间应大于该截尾数据,对排列其他故障时间间隔能起到一定参照作用,故而不能忽略。具体使用时需要进行修正,修正所得的次序被叫做故障间隔时间的秩次,本课题运用平均秩次法处理:综合各家族变压器的故障间隔时间及截尾数据,按照由小至大排序,次序记为i(i=1,2,3,…,Ng),Ng代表的是数据总量,存在Ns个数据是故障间隔时间。按由小至大排列所有故障间隔时间,记作tj(j=1,2,3,…,Ns)。引进秩增量△Atj,运用序列{ (tj,D(tj) ) }估算α、β[2]:
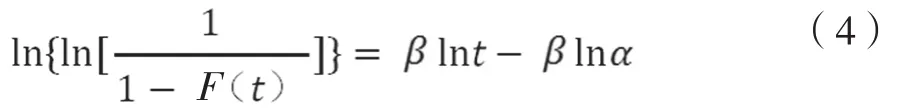
3 故障智能诊断方法
绝大多数干式变压器事故内,设备内热量骤然增加,促进绝缘老化进程。且不同类型、位置的绝缘故障会使变压器内部各部位出现程度不一的温升情况,即其热点温度和位置及故障类型有关。故而,由变压器的温度场方面开展分析,模拟变压器温度场,探查设备现在各种故障运转状态下的热点部位与温度,进而使其后期运行时发生该类故障时能快速、精准判断其类型及部位,使运行的可靠性、经济性得到保障。
3.1 温度场仿真
ANSYS、Fluent、COMS OL等均是常用的有限元分析法(FEM),本文建模选用SCB10-1000/10型干式变压器(见图1)。

图1 干式变压器简化三维模型
建模完成后,要将相应的材料属性添加到其内。变压器铁心材料是硅钢片,基于BH插值表导入期磁化曲线,高低压绕组材料有铜线与铜箔之分,空气作为冷却流体,层流模型作为流体模型,自然对流ah=6。
高压侧额定相电流、相电压分别是57.735A、5773.5V,低压侧额定相电流、相电压分别为1443.4A、230.94V。给有限元模型施加激励,具体是在高、低压侧分别施加三相电压、三相负载电流。求解电磁场以后,能顺利得到高压侧电流及低压侧电压值。计算验证了电磁仿真模型的准确性[3]。
变压器额定运行时,铁心及绕组损耗是其内部热量的主要来源。仿真运算得到,在50Hz工况下,铁心、绕组损耗分别约2.17kW、8.73kW。设定仿真环境是20℃,热辐射系数0.9,变压器处在额定运行状态中。
仿真模拟变压器各种故障运行状态下的温度场时,设置45个“温度传感器”用于提起温度场内的温度数据。针对绝缘退化破损情况,主要仿真模拟变压器高压绕组匝间绝缘退化工况下温度分布情况,具体把高压绕组中间作为切面,设定距离该切面一定高度(10mm)的绕组区都是因绝缘破损而发生匝间短路的绕组部分,即是额外施加固定热源的部分。
按照以上运行方式仿真一共获得675个温度数据,依照三项对应构成一组的原则分成225组。比如变压器额定运行时的各温度测点数据内的(AC3,BC3,CC3)构成一组,与之相对应的温度数据是(62.62,68.03,64.60),把以上数据作为下一节内机器算法的训练集与测试集。
3.2 基于GA完善的SVM计算模型
引进GA算法的宗旨是搜索优化SVM算法内的核带宽σ、惩罚因子Cc。鉴于此,可以顺利获得基于GA优化后的SVM运算流程:
1)设置好σ、Cc各自的取值区间,随机生成数个样本;
2)抽调出Nh个样本组成原始种群;对全部种群个体的两个参数采用二进制编码处理以生成基因串,具体构成如图2[4]所示;
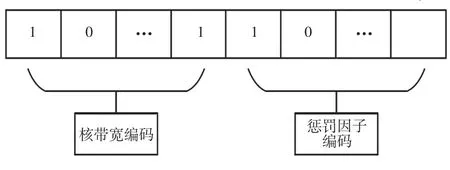
图2 基因串二进制编码形式
3)解码种群内个体基因串,带入参数SVM,用训练集和测试集数据进行相应训练集检测,获得准确率;
4)运输出全部个体的适应度Sui;
5)判断是否符合设计的终止条件,满足就退离循环,终止遗传优化过程,否则执行6);
6)遗传操作,生成新的种群。结合个体适应度选择进到下一代种群的个体数,某一个体进到下一代的概率是Pi:

分别用“基本位变异”、“单点交叉”进行变异、交叉操作。
7)返回到步骤3)继续实施。
把以上步骤制成流程图(见图3)[5]。
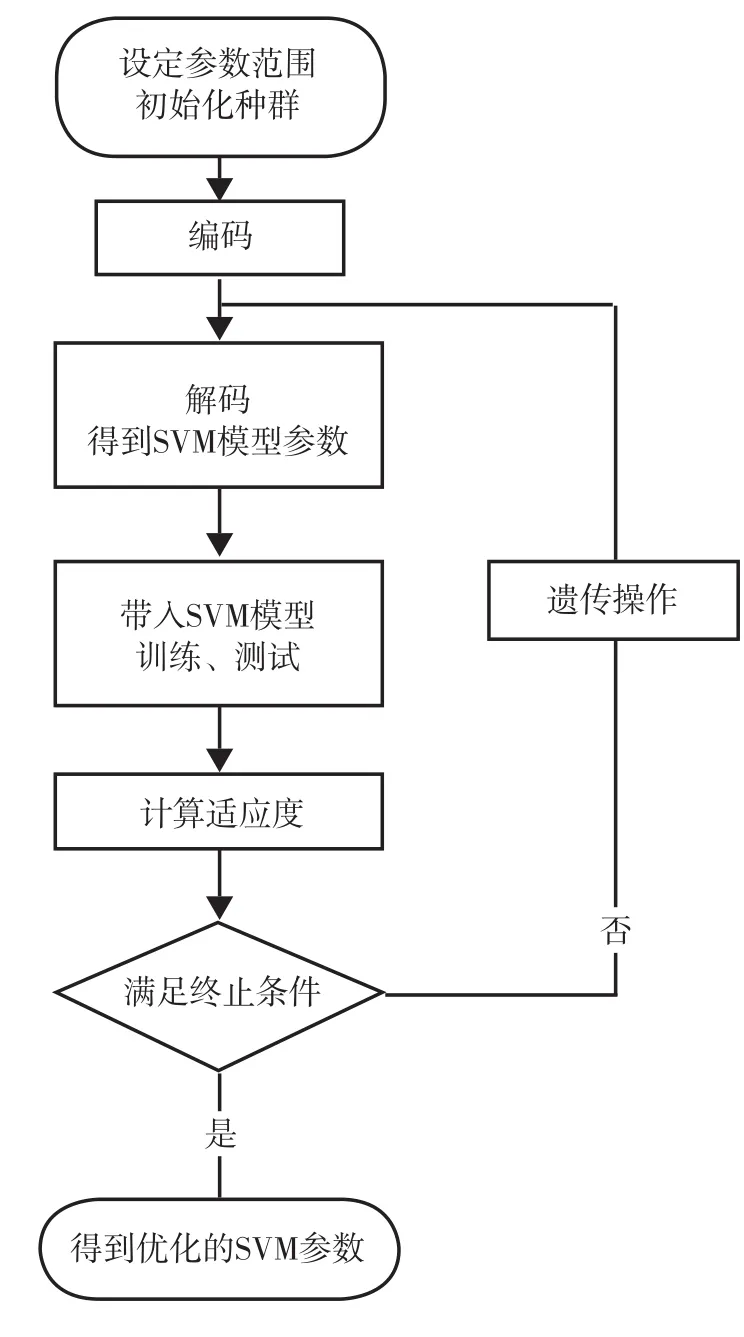
图3 基于 GA 优化的SVM运算流程
3.3 故障诊断模型的测试结果
3.3.1 设置数据分类和算法参数
本课题运用 Python达到基于GA优化的SVM故障诊断算法,关于仿真数据的分类,全部数据组分分别属于5种运行状态内的一种,为便于论述,把正常运作、高压击穿、局部放电、瞬时冲击大电流、绝缘退化状态分别记作1、2、3、4、5。设定一个完整的数据组格式是(Ap_t,Bp_t,Cp_t,"stat_num"),前三个数据是温度数据,最后一个数据是其所属运行状态的编号。本次测试训练、测试数据分别有150组、75组。
关于SVM模型参数的设置问题,选用高斯核作为映射函数,取松弛参数85,核带宽α、惩罚因子Cc的寻优范围分别是[0.001,500]、[0.01,1000]。
GA的编码长度是每个参数20位,种群100,最大迭代次数200,交叉概率0.9,变异概率0.01。迭代终止条件有两个,其一是有个体适应度抵达85%,其二是迭代次数达到最大值。在交叉操作中,选择了基因串内第10位作为分界点进行单点交叉操作。
3.3.2 算法仿真结果
具体是把SVM故障诊断算法进行以训练集和测试集为基础的学习、检测测试,绘制出个体适应度曲线(见图4)[6]。个体适应度是个代所有个体的适应度均值,各代个体内个体适应度最大值被认定是最佳适应度。
观察图4,尽管平均适应度始终处于变动状态,但SVM算法的最佳适应度在迭代10次之内就已获得一个较高值,但是随后就进入到这个局部最优解。据此可以推测,如果不用GA对SVM进行优化处理,那么最后结果可能是这个局部最优解的81.33%,证实了运用GA算法的必要性。

图4 适应度变化曲线
最后所得的最优参数是:σ=0.0817、Cc=758.88。训练集、测试集内分别存在11个、13个错误,精准度分别达到92.67%、82.67%。表明算法具有较高的精准性,能实现对干式变压器运行故障的有效分类。
4 结束语
本课题中建设了干式变压器的三维结构模型,运用COMSOL 对变压器正常运行状态下的温度场进行仿真,解读其内部温度分布规律,在此基础上仿真变压器常见5种运作方式下的温度场数据,最后参照设备故障数据特征,在遗传算法优化的支持下开展故障诊断。统计测试结果,计算出算法诊断的精确率达到82.67%,验证这种方法的有效性、可行性,具备一定推广价值。

