基于单指数、峰度与拉伸指数扩散成像模型的磁共振检查在预测前列腺癌分级中的价值研究

梁 媛，侯召瑞，王 瑞，王 玉，秦 智，王远成

东南大学附属中大医院影像科，江苏 南京 210009

随着医疗技术的发展，人口老龄化现象日趋明显，在我国中老年男性群体中，前列腺癌（prostate⁃cancer，PCa）患者数量日益增加［1］。Gleason 评分是一种被广泛采用的PCa 组织学分级方法［2］，为主要结构类型与次要结构类型评分之和，评分越高代表PCa 分化程度越差［3］；根据ISUP 2014 PCa 分级分组标准，Gleason评分与预后分组对应［2］。目前对于PCa的诊断，已有很多检查方法，其中包括超声检查和磁共振成像（magnetic resonance imaging，MRI），穿刺活检依然是术前诊断和组织学分级的最终标准［4］。MRI 作为一种非侵入性检查，因其软组织分辨率较高，且可进行多参数、多方位的成像，临床应用范围越来越广泛［5］，近年来出现的许多新的MRI技术，更是给临床带来了更多有价值的信息。MRI中扩散加权成像（diffusion weighte dimaging，DWI）可以用于评估肿瘤细胞增殖和肿瘤坏死的程度［6］。传统DWI单指数模型中，只能提供表观扩散系数（apparent diffu⁃sion coefficient，ADC），由于细胞中水分子扩散运动呈非高斯分布，导致该单一高斯模型指数无法详尽描述扩散情况。近年来出现了一些高级模型，如体素内不相干运动（intravoxel incoherent motion，IVIM）、分数阶微积分模型（fractional order calculus，FROC）、扩散峰度成像（diffusion kurtosis imaging，DKI）、拉伸指数模型（stretched exponential model，SEM）等，这些高级模型可以提供更多的参数。如DKI 可以提供平均扩散系数（mean diffusivity，MD）和平均峰度（mean kurtosis，MK）［7-8］，SEM 可提供扩散分布指数（distributed diffusion coefficient，DDC）和扩散异质性指数（α）［9-10］，这些参数消除了非高斯分布的影响，能更准确地描述组织中水分子的扩散运动。本研究通过计算前列腺MRI 中DWI 数据得到DKI 和SEM 各参数，并与术后病理结果中的预后分组进行回归分析，评价各参数与预后分组的相关性，从而评估上述模型各参数区分PCa恶性程度、判断预后的价值。

1 对象和方法

1.1 对象

本研究经东南大学附属中大医院伦理委员会批准（2022ZDSYLL030⁃P01），所有受试者知情同意。回顾性收集2019 年11 月—2021 年9 月在东南大学附属中大医院行PCa切除术的患者71例，年龄54～88岁，平均年龄75岁。纳入标准：通过手术病理诊断为PCa 的患者；术前MRI 检查使用了多b 值DWI 序列。排除标准：未查到术后病理结果；病灶太小，无法进行测量；因运动、金属物等产生伪影影响观察。在本研究中以Gleason 评分进行预后分组。Gleason评分≤6为预后分组1，Gleason评分3+4为预后分组2，Gleason 评分4+3为预后分组3，Glea⁃son评分8为预后分组4，Gleason评分9和10为预后分组5。其中预后分组为1 的7 例，预后分组为2 的13例，预后分组为3的14例，预后分组为4的24例，预后分组为5的13例。

1.2 方法

1.2.1 成像仪器及序列参数

本研究数据均为Philips Ingenia 3.0T 磁共振扫描，采集线圈为16 通道矩阵线圈。DWI 序列参数为：TR为6 000 ms，TE为70 ms，层厚为4.0 mm，层间距为0.4 mm，FOV 为200 mm×300 mm，矩阵为80×142，b值（s/mm2）/平均次数为：0/1、1000/2、2000/3。

1.2.2 图像后处理

在PACS 系统中获取患者MRI 的DICOM 图像，使用MathWorks 公司的MATLAB 2018b 软件编写图像处理程序［11］，根据以下模型方程进行DKI 和SEM拟合，并输出到各个单独的参数图中：

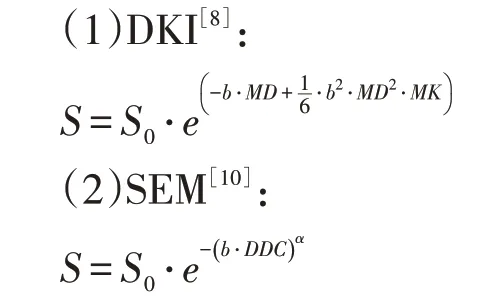
其中，S代表扩散加权因子为b时的信号强度；S0代表b为0时的信号强度。MD代表DKI模型中组织内平均扩散速率；MK表示扩散系数的峰度；DDC代表SEM 模型中校正后的扩散系数；α代表SEM 模型中扩散异质性指数。传统单指数模型的ADC 由仪器自带的图像处理程序自动生成。结合术后病理结果，由两位高年资影像诊断医师在DWI图像中，依据病理学提示的病灶位置，在病灶中间层面，尽可能大地勾画类圆形感兴趣区（region of interest，ROI）；若有多个病灶且Gleason评分不同的，取评分最高的一个病灶；勾画时避开出血、坏死及测量值为0的区域；将ROI复制到ADC、DDC、α、MD、MK参数图中，将每个参数的平均值及SD进行记录；将两位医师对每个ROI测量的数据取平均值进行统计。

1.3 统计学方法

使用SPSS 22.0 软件进行统计学分析。计量数据取两位医师统计数据的平均值，不符合正态分布的计量资料用中位数（四分位数）［M（P25，P75）］表示（表1）。以Cronbach’s Alpha 系数来评价二者间的可信任度，＞0.8表示可信任度好。在验证数据可信任度后，分别对各参数在各组间的分布差异用Krus⁃kal⁃Wallis 检验，P<0.05 为差异有统计学意义。将ADC 分别与DDC、MD 进行Wilcoxon 秩检验，P<0.05视为分布差异有统计学意义。对各参数与预后分组之间的相关性使用Spearman相关性分析，根据相关系数r的大小评价相关性强弱，当其绝对值处于以下区间时：［0，0.2）认为不相关，［0.2，0.4］认为相关性低，（0.4，0.6］认为相关性中等，（0.6，0.8］认为相关性强，（0.8，1.0］认为极具相关性［12］。对各组参数与预后分组进行曲线拟合，为了得到单一趋势、拟合效果好且数值唯一的拟合曲线，本研究用线性和逆模型两种曲线进行拟合，以R2评价拟合度高低。

2 结果

2.1 医师操作可信任度检验结果

两位医师间的评分数据Cronbach’s Alpha 系数为0.910，证明二者评分数据可信任度高。

2.2 各参数在各分组上的Kruskal⁃Wallis检验结果

ADC、α、DDC、MD、MK 在各预后分组上的分布均存在差异（P均<0.05，表1）。

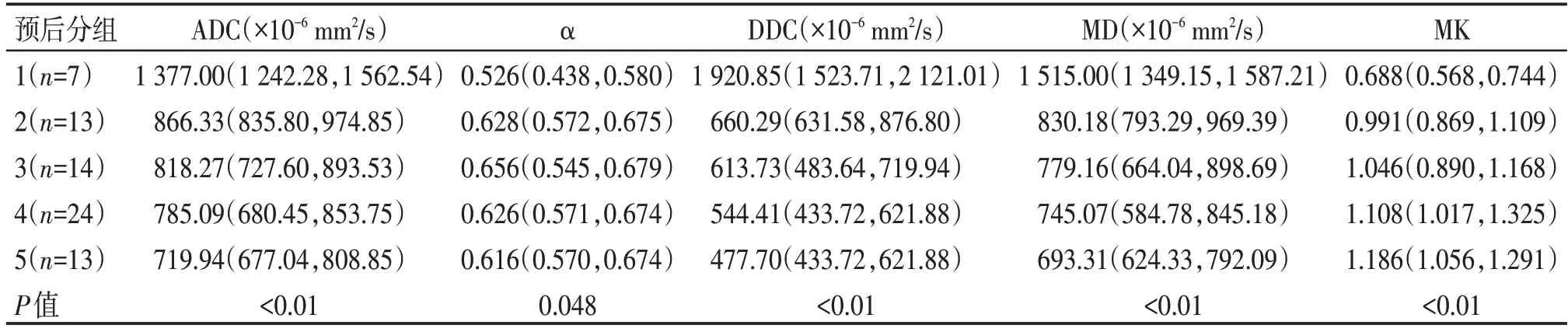
表1 不同分组的ADC及DKI、SEM各参数的比较 ［M（P25，P75）］

2.3 ADC分别与DDC、MD的Wilcoxon秩检验结果

ADC 与DDC 在各预后分组上的分布存在显著差异（P<0.01）；ADC与MD在各预后分组上的分布差异均无统计学意义（P>0.05）。

2.4 各参数与预后分组之间的Spearman 相关性分析结果

ADC、DDC、MD 与预后分组均成负相关（r值分别为-0.601、-0.627、-0.566，P均<0.01）；MK 与预后分组呈正相关（r=0.537，P<0.01）；α与预后分组相关性较弱（r=0.239，P=0.045）。

2.5 各组参数与预后分组的曲线拟合结果

ADC 与预后分组以线性模型拟合的R2为0.452，逆模型的R2为0.644；DDC与预后分组以线性模型拟合的R2为0.470，逆模型的R2为0.749；MD 与预后分组以线性模型拟合的R2为0.436，逆模型的R2为0.643；MK 与预后分组以线性模型拟合的R2为0.302，逆模型的R2为0.345；α与预后分组的以线性模型拟合的R2为0.116，逆模型的R2为0.174（图1）。各分组在预后分布上总体呈下降趋势，且DDC 比ADC 和MD 有更大的斜率，在低级别中DDC 数值普遍高于ADC，在高级别中DDC普遍低于ADC（图2）。预后分组1、2 组典型病例ADC 和DDC 对比情况见图3。

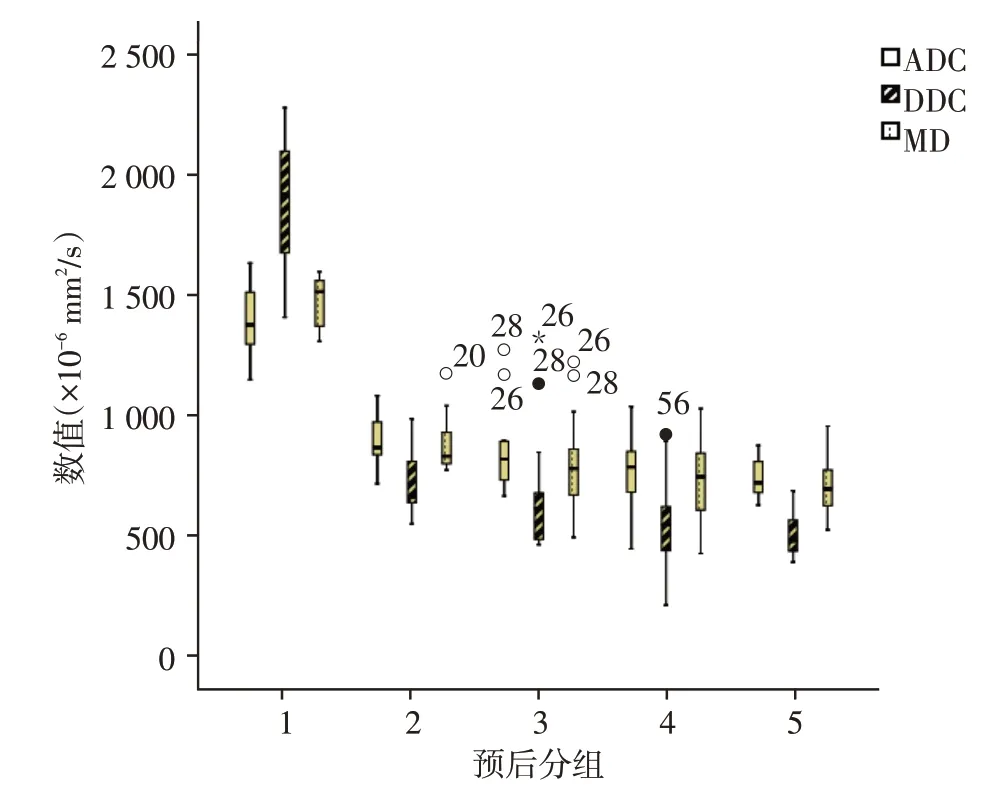
图2 ADC、DDC、MD在预后分组上的分布

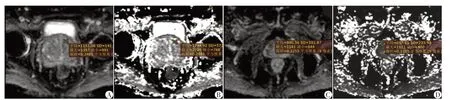
图3 患者ADC和DDC对比

3 讨论

DWI 是MRI 中的常规扫描。传统单指数扩散模型只能提供ADC这个单一数据［13］，但由于组织细胞分布的不均匀性，水分子在其中的扩散运动不符合高斯分布，ADC作为高斯模型［14-15］，无法将这种运动详尽描述。DKI 和SEM 模型提供校正系数MK、α，二者以非线性校正得出ADC的校正值MD、DDC，能更好地拟合高b 值中扩散信号的非线性下降趋势，从而描述水分子的非高斯运动［16-17］，进而反映组织细胞的分布和均匀度［18］。以往文献中已有将单指数、DKI或SEM模型应用于PCa的诊断中，但三者联合进行评价的文献较少；本研究的优势在于分别对ADC、DDC、MD 与预后分组进行回归分析，以拟合度R2的大小评价三者在预测肿瘤细胞学分级中的能力。

本研究对各参数在5个预后分组之间的分布进行对比时发现，根据Kruskal⁃Wallis检验结果，ADC、α、DDC、MD、MK 的分布均存在差异。将ADC 分别与DDC、MD进行Wilcoxon秩检验发现，ADC与DDC的分布存在显著差异；ADC 与MD 的分布差异无统计学意义。在分别对各参数与预后分组进行曲线拟合时，发现ADC、DDC、MD 与预后分组均呈负相关（r值分别为-0.601、-0.627、-0.566），且以逆模型的拟合度较高（R2分别为0.644、0.749、0.643）；MK与预后分组呈正相关（r=0.537），逆模型的R2为0.345；α与预后分组的曲线拟合度较低（r=0.239）。这说明3 种模型和预后分组均呈现较强的相关性，ADC 作为经典的扩散系数模型在判断PCa预后有很高的价值，SEM和DKI模型在这一方面也有较好的表现［19］。

SEM 模型中的DDC 比单指数模型的ADC 与预后分组的相关性更强［20-21］，可能是因为ADC 作为高斯模型，无法详尽表达非高斯模型的弥散运动，而DDC是校正非高斯运动后的ADC，所以DDC在一定程度上更能描述水分子弥散受限程度。在和预后分组的拟合曲线上，DDC有着比ADC斜率更大的切线（图1）。不同预后分组DDC数值上的差异比ADC大，特别是1 组和2 组之间的差异最为明显（图2），在低级别中，DDC 数值普遍高于ADC，在高级别中DDC 普遍低于ADC（图2、3）。可见，在通过扩散成像的各参数的值，对Gleason 评分进行预测时，DDC的敏感度高于ADC。本研究发现拉伸指数校正系数α与预后分组的相关性较弱，与郭然等［11］对肝细胞癌的研究以及马彦云等［18］对乳腺癌的研究结果有差异，这可能与PCa分为中央带、外周带、移行带［22］，而不是一个均质整体，且各分区组织细胞的组成之间存在差异有关，但本研究未对不同分区进行细化分组，今后可以细化到前列腺的某个单独分区来进一步研究。

DKI模型中的MD［23-24］与预后分组的相关性，理论上应优于ADC，但在本研究中二者在不同预后分组上的分布没有显著差异，且二者与预后分组的曲线拟合度也几乎一致（R2分别为0.644、0.643），故二者在预测PCa 的Gleason 评分方面，意义基本相当。本研究中发现MK与预后分组呈正相关，这与赵芯一等［25］的研究结果一致。随着肿瘤恶性程度提高，水分子扩散运动受限更加明显，且组织结构变得更加混杂［26］，进而水分子的扩散偏离高斯分布的程度更大［27］，而MK 描述的是该扩散偏离高斯分布的程度，故与预后分组呈正相关。

本研究的局限性在于，由于EPI⁃DWI 序列矩阵和分辨率比较低，以致有些较小病灶所占的像素比较少，不能进行有效测量。在今后研究中可以对序列参数进行优化［28-30］。

综上所述，PCa预后分组的预判中，单指数模型仍是实际应用中性价比最高的方法，SEM模型中的DDC 有比ADC 更优秀的表现，DKI 模型中的MD 和ADC的表现相当。