强降雨环境下堆积层滑坡稳定性研究

邹 建

（贵州正业工程技术投资有限公司，贵州 贵阳 550001）

亚热带地区和热带地区的堆积层滑坡较多，强降雨环境下堆积层滑坡引发的自然灾害问题较多，对人身安全及财产造成威胁。为了减少滑坡问题带来的影响，需要对强降雨环境下的堆积层滑坡稳定性进行分析，根据稳定性分析结果，采取一些应对措施做好防范工作。在进行降雨滑坡稳定性分析时，除了降雨入渗分析以外，还需要对稳定性评价方法进行深入探究。目前，GA模型（Green-Ampt模型）降雨滑坡稳定性分析方法应用较多，该模型虽然能够反映雨水重分布状况，分析降雨量对边坡稳定性造成的影响，但是未能考虑湿润锋以上饱和带平行坡比表条件下引发渗漏而导致的水分流失问题，且缺少降雨入渗导致的土体抗剪强度变化分析。为了弥补该模型存在的不足，该文尝试提出新的滑坡降雨入渗模型研究，利用该模型分析堆积层滑坡稳定性。

1 滑坡降雨入渗模型的构建

1.1 模型假设

堆积层滑坡稳定性分析，需要获取滑坡降雨入渗信息，通过分析入渗特点，判断滑坡稳定性。通过整理大量文献资料发现，强降雨环境下，斜坡浅表层土体状态发生改变，待其达到饱和状态后，随着降雨量的增加逐渐扩展，该过程可以从2个方面进行分析：1）饱和带随着雨水渗入补给的增加而逐渐扩大。2）水力梯度、坡体几何条件容易对滑坡降雨入渗造成较大影响，饱和带水分沿着坡表向下的方向排出，以渗透力方式作用于滑坡。基于这些分析，探究滑坡强降雨入渗过程，提出以下假设。1）滑坡结构分为2个部分，均质土体分布在上部，不透水基岩分布在下部。2）根据滑坡结构特点可知，坡表径流环境下，坡面不会产生积水。3）土体含水率分布均匀，去除地下水作用指标展开分析，基质吸力水头参数为固定值。4）沿着竖直向下的方向降雨，产生的强度不低于土体饱和渗透系数。

1.2 模型的构建

滑坡非饱和土体受地表水渗入影响，导致表层土体结构发生变化，逐渐达到饱和状态。在该过程中，基质吸力和重力的作用下，入渗持续期间，湿润锋随之向下扩展。按照GA模型结构和特点，分析表面倾斜边坡结构变化。表层土体受强降雨影响形成饱和带，计算入渗速率，如公式（1）所示。

式中：为斜坡表面倾角；H为湿润锋位置的基质吸力水头；λ为饱和渗透系数；为降雨入渗速度；D为沿着坡表垂直方向的湿润锋深度。

由于降雨初期，表层土体没有达到饱和状态，此时未产生湿润锋。上述模型适用条件有限，待形成湿润锋以后，或者表层土体达到饱和状态后，才可以使用该模型进行分析。为了较为全面地探究滑坡降雨入渗问题，将入渗过程分为2个阶段，分别是湿润锋形成前阶段、湿润锋形成后阶段。

与降雨强度相比，坡表土体雨水渗透能力更强，处于非饱和状态，阴雨天气所降雨水皆渗入土体。当降雨持续一段时间达到临界时刻t，便形成湿润锋。假设降雨强度为q，根据入渗率与强度之间的关系，设定降雨入渗速率为cos。将这2个参数代入公式（1）中，得到关系式（2）。

式中：D为t时刻对应的湿润锋深度，为降雨强度。

假设t时刻降雨入渗累计量为Q，该参数计算公式如下。

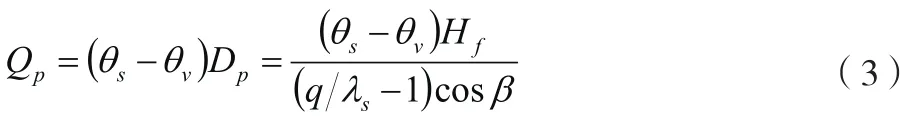
式中：θ为土体天然体积含水率，θ为土体饱和体积含水率。按照质量守恒定律，土体水分增加量与降雨量相等，由此可以推导临界时刻的计算方法，如公式（4）所示。

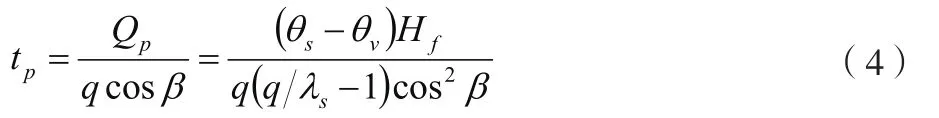
滑坡表层土体达到饱和状态的同时，部分区域产生表层径流，这些区域雨水入渗能力不高于降雨强度。其中，关于表层入渗速率可以利用公式（1）展开计算。另外，水力梯度、斜坡几何条件皆对雨水入渗性能造成一定影响，湿润锋以上饱和带水分沿着坡表向下的方向流动，以坡脚作为雨水排出区域。以往关于斜坡降雨问题的探究，利用GA模型展开分析。该研究方法缺少饱和带与坡表层平行方向的降雨渗流问题，这与实际情况不符。为了弥补GA模型的不足，本研究构建了新的湿润锋计算模型，如图1所示。

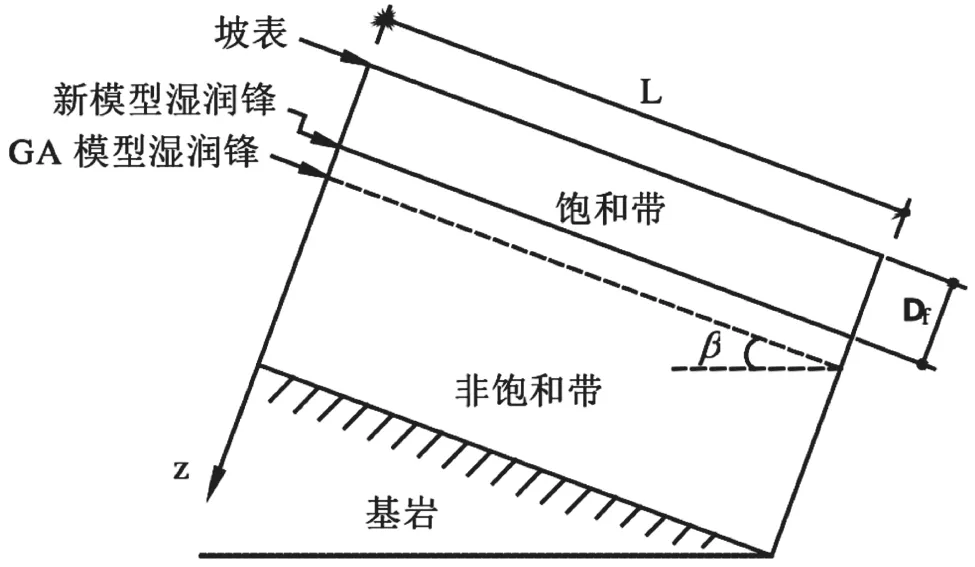
图1 GA模型与新模型湿润锋的比较

将GA模型与新模型湿润锋进行对比，根据模型关系，对湿润锋形成后阶段的降雨入渗采取补给处理。关于降雨入渗问题的分析，可以利用公式（1）进行计算，得到降雨累计入渗量，参数计算公式如下。

累计降雨入渗量对时间展开求导计算，得到降雨入渗速率。采用求导计算方法，对公式（5）求导，所得结果代入公式（1）中。对计算结果进行整理，获取湿润锋速率。另外，考虑到饱和带平行于坡表渗流，排除一些水分，导致湿润锋深度减少。引入达西定律，分析湿润锋减少速率和实际深度扩展速率，对2个参数进行积分计算，将积分计算结果代入初始条件，获取湿润锋动态变化规律。由此可以推断，土体性质、滑坡几何参数等多个因素与湿润锋深度实际参数密切相关。与GA模型相比，新的湿润锋模型能够较为显著地体现降雨入渗滑坡尺寸效应。因此，该模型更贴合实际，可以作为滑坡稳定性分析工具。

2 基于强降雨环境的堆积层滑坡稳定性分析

2.1 整体抗剪强度

该研究对持续降雨过程中滑坡稳定性的分析，在土体抗剪强度基础上，运用极限平衡法求解。其中，强度的选取非常重要。

土体在天然环境中呈现非饱和状态，按照相互独立双应力状态变量求解方法，计算该状态的强度，如公式（6）所示。

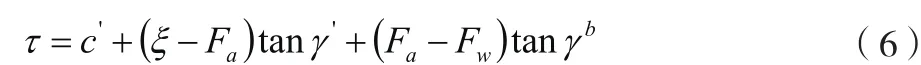
式中：γ代表摩擦角，用于描述基质吸力增加程度；代表总正应力；F代表孔隙水压力；F代表孔隙气压力；'代表有效内摩擦角；'代表土体有效黏聚力；F-F代表基质吸力。

正应力与基质吸力之间相互独立，所以，该研究将黏聚力贡献用基质吸力来描述，由此对表观黏聚力进行定义，用基质吸力贡献与有效黏聚力之和描述。考虑到滑坡土体的含水率在降雨过程中分布不均匀，加大了土体物料状态分析难度。为了简化问题，该研究用公式（7）描述抗剪强度。

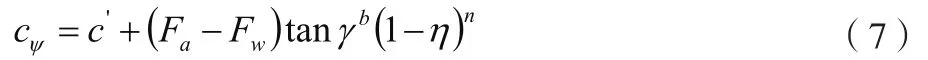
式中：代表试验参数（通常取值3.4）；代表饱和层高度比，计算方法为=h/。其中，代表土体条块高度；h代表沿着竖向的饱和层高度，计算方法为h=z/cos；c代表表观黏聚力。

由此推断整体土层抗剪强度的计算公式，如公式（8）所示。

2.2 模型稳定系数计算

关于稳定系数的计算，取一竖直土条块作为分析对象，假设坡体滑面与表面处于平行状态，受力情况如图2所示。

图2 土体条块受力

其中，土条重力的计算如公式（9）所示。

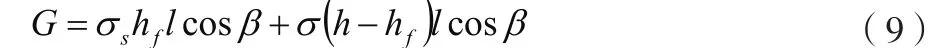
式中：σ代表土体的饱和重度，代表天然重度，代表沿着坡表面方向的土条块长度。

土条块受饱和带水体渗透影响，沿着坡表面平行方向产生渗透力，该参数的求解公式如下。

式中：σ代表水重度。

假设稳定性系数为Φ，利用该系数评价滑坡稳定性。其中，Φ为抗滑力与下滑力的比值，通过计算Φ，分析土条块受力情况。以下为系数Φ的计算公式。

式中：当Φ＞1时，滑坡处于稳定状态；当Φ＜1时，滑坡处于不稳定状态。利用该公式计算稳定性系数，能够获取土体整体强度在降雨过程中发生的变化特征信息，可以将其作为土体渗透力分析参考依据，所得分析结论与实际情况更加贴合。

3 结果分析

3.1 降雨时间推移下的不同坡长时湿润锋深度变化规律

该研究在GA模型基础上，构建斜坡强降雨入渗分析模型。该模型中融入了饱和带平行坡表条件下的渗透作用，解决了边坡长度分析不足的问题。本次测试设定滑坡模型的倾角为30°，厚度为3.9 m的粉质黏土覆盖在滑坡表面，各项参数分别如下。σ=19.4kN/m，=16.4kN/m，λ=110m/s，'=28°，=5kPa，H =50cm，θ=0.44，θ=0.14（F-F）tanγ=10kPa。取不同坡长，计算降雨时间推移下的湿润锋深度数值，分析其变化规律。其中，坡长取值5 m、10 m、30m以及60 m，计算结果见表1。本次统计以时间为0~10×10s的不同坡长的湿润锋深度作为统计指标，设定时间间隔为1×10s。

表1 降雨时间推移下的不同坡长的湿润锋深度变化

表1中，持续降雨过程中，湿润锋深度逐渐增加，并且随着坡长的增加数值逐渐变大。GA模型的湿润锋深度从0.00 m增加至4.00 m，当降雨时间不足4×10s时，湿润锋深度增加幅度较大。当降雨时间超出4×10s后，湿润锋深度增加幅度发生变化较大，增加幅度先变大而后变小，再次变大。不同降雨时间为1×10s时，=5m条件下的湿润锋深度最小，随着降雨时间的推移，湿润锋深度逐渐增加，但是小于其他取值条件下的湿润锋深度数值。当不同降雨时间超过2×10s后，=60m条件下的湿润锋深度最大。从整体来看，滑坡的坡长越小，湿润锋扩展受饱和带渗流的影响越小，造成的影响作用逐渐增加。当坡长趋于无限大时，饱和带渗流不考虑其中，可以简化该模型结构，看作GA模型。相比之下，该模型的湿润锋深度特性分析更加全面。

3.2 降雨时间推移下的不同方法计算稳定性系数变化规律

该研究以传统分析方法、“整体强度+不考虑渗透力”分析方法作为参照，检验该文提出的“整体强度+考虑渗透力”分析方法在稳定性系数变化规律分析中的可靠性。关于不同方法计算稳定性系数在降雨时间推移下的变化统计结果见表2。本次统计以时间为0~8×10s的不同方法计算稳定性系数作为统计指标。

表2 降雨时间推移下的不同方法计算稳定性系数变化

表2中，传统方法应用下的稳定系数计算结果几乎没有受到降雨时间推移的影响，随着降雨时间的推移，稳定性系数下降幅度较小，从1.55下降至1.44，该变化现象与降雨边坡稳定性实际情况完全不符。在不考虑渗透力影响的情况下，分析滑坡整体强度，统计降雨滑坡稳定性数据，持续8×10s降雨，稳定性系数从1.55下降至1.05。由此推断，“整体强度+不考虑渗透力”方法应用产生结果受降雨影响不是很显著。而考虑渗透力影响的情况下，分析滑坡整体强度，统计获取的降雨滑坡稳定性数据受降雨影响较为显著，持续8×10s降雨，稳定性系数从1.55下降至0.65，稳定性系数统计结果与实际情况相符。因此，该研究构建的“整体强度+考虑渗透力”模型可以作为滑坡稳定性分析工具。

4 结语

该文围绕强降雨环境下堆积层滑坡稳定性分析方法进行探究，在GA模型基础上进行优化，构建新的分析模型。将考虑渗透力影响、滑坡整体强度分析综合到一起，优化滑坡稳定性模型。应用结果表明，该模型不受滑坡坡长限定影响，能够较为全面地分析湿润锋深度特性，并且计算所得降雨滑坡稳定性数据与实际情况相符程度更高，可以作为滑坡稳定性分析工具。