基于卡尔曼滤波、分形和LSTM的大坝变形趋势分析方法

邓思源，周兰庭，柳志坤

(1.河海大学水利水电学院，江苏 南京 210098；2.青岛市发展和改革委员会动能转换推进处，山东 青岛 266000； 3.青岛市经济发展研究院，山东 青岛 266000)

随着水利资源的深入开发，坝址的地质条件越来越复杂，大坝的规模也向高、大方向发展[1-2]。为了保障大坝运行的安全性，高效可靠的大坝变形监测及趋势预报变得愈发重要。然而，在大坝变形监测过程中，变形监测数据易受噪声污染，增加了监测过程及趋势分析的难度，同时，大坝变形呈现显著的非线性特征，给预报的准确性带来考验，使得大坝变形趋势更加难以预估。

针对上述问题，许多学者进行了探讨和研究，构建出一系列较为可靠、适用的大坝变形趋势分析预测模型或理论。如李子阳等[3]综合考虑去噪与时变功能，基于Kalman滤波方程组，结合统计模型和ARMA等方法，提出了一种能反映大坝性态变化和变形发展趋势的时变Kalman预测模型；刘亮亮等[4]针对混凝土坝变形呈现显著的非线性特征，引入分形插值理论，提出了一种可行有效的混凝土坝趋势分析方法；郝永河等[5]基于变形信息分解，将R/S分析法同优化极限学习机及混沌理论结合，融合定性分析和定量预测结果，实现了较为可靠的大坝变形趋势预报；牛景太[6]提出了基于奇异谱分析与粒子群算法优化支持向量机的混凝土坝变形监控模型。这些模型虽均具有一定的有效性和适用性，却囿于对大坝变形趋势某单一方面的分析研究，缺乏对该类问题多方面的综合考虑，故而存在未充分考虑干扰和噪声、未充分挖掘变形监测数据的时间依赖性、模型参数难以确定、构建数学模型过程复杂、长期预报能力不足等问题，导致模型存在一定的局限性。因此，亟待从多方面着手，引入先进的理论方法，并充分融合各自优势，进而提升大坝变形趋势分析的综合性和可靠性。

鉴于此，考虑到卡尔曼滤波[7-8]在削减干扰和噪声方面的优势、分形理论[9-10]在解析判断呈现较强非线性和时间相关性特征的数据方面的适用性以及长短时记忆神经(long short-term memory neural network，LSTM)模型[11-12]在分析处理具有典型动态特性的时间序列时优秀的应用表现，本文将三者进行优势融合，提出了一种基于卡尔曼滤波、分形和LSTM模型的大坝变形趋势综合分析方法，可实现从定性和定量的层面对大坝未来变形趋势进行综合分析评价，从而更为可靠掌握大坝未来变形的发展趋势。

1 基本理论

1.1 卡尔曼滤波

卡尔曼滤波是从与被提取信号有关的观测量中通过算法估计出所需信号的一种滤波算法，特别适用于数据量大且具有显著非平稳性的大坝变形监测数据[8]。依据文献[13]推导，可得其状态方程和观测方程分别为

Xk=Ck|k-1Xk-1+Wk-1(k=1,2,…)

(1)

Yk=MkXk+Vk(k=1,2,…)

(2)

式中：Xk、Yk分别为tk时刻的状态矢量和观测矢量；Ck|k-1为从tk-1时刻到tk时刻的系统一步状态转移矩阵；Mk为观测矩阵；Wk-1、Vk分别为系统噪声矢量和观测噪声矢量。

对于系统噪声和观测噪声两序列的统计特性，可作以下假定：

(3)

式中：Qk、Rk分别为系统噪声矢量和观测噪声矢量的方差矩阵；δkj为狄拉克(Dirac)函数，当k=j时，δkj=1，否则δkj=0；E为数学期望；Cov为协方差。

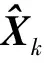
(4)

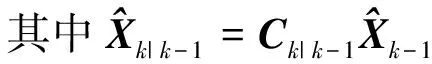
Pk=(I-KkMk)Pk|k-1

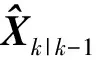
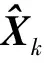
1.2 分形理论

分形理论是研究事物分形性质及其应用的科学理论，其中R/S分析法是分形理论中的一种分析方法。R/S分析法又称为重标极差分析法，是由Hurst[14]在探讨尼罗河水库水位波动的规律时首先提出的。

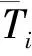
(5)

(6)

每个子序列Ti的累积偏差为

(7)

累积偏差的极差阈值为

Ri=maxLj,i-minLj,i

(8)

结合式(6)和(8)得到子序列的重标极差Ri/Si，即

(9)

对各子序列Ri/Si求均值即可得到相应尺度下的(R/S)n，即

(10)

改变n的取值，重复上述步骤，求取不同尺度下对应的(R/S)n值，再经过统计分析，即可获得 (R/S)n值同Hurst指数H之间具有如下关系：

(R/S)n=CnH

(11)

式中C为拟合参数。

根据式(11)可得到Hurst指数。Hurst指数又称为分形指数，常用于时间序列的趋势性评价，具有较强的预报功能。通过随机试验总结发现，Hurst指数存在如下性质：当01的情况，则表明时间序列中存在确定性误差，不具备分析价值。

进一步可得R/S分析法的统计量Vn计算公式如下：

(12)

根据文献[15]，Hurst指数和豪斯道夫维数D存在下述关系：

D=2-H

(13)

1.3 LSTM

LSTM由Hochreiter等提出[16]，由于其能够学习长期顺序依存关系，具有从经验中学习的能力，目前被广泛应用于时间序列的预测。LSTM通常由输入门、忘记门、输出门3个门组成[17]。

忘记门的作用是控制细胞状态中信息的取舍：

ft=σ(Whfht-1+Wxfxt+bf)

(14)

输入门的作用是更新细胞状态中的信息：

it=σ(Whiht-1+Wxixt+bi)

(15)

(16)

(17)

输出门控制着需要输出的信息：

ot=σ(Whoht-1+Wxoxt+bo)

(18)

ht=ottanh(Ct)

(19)

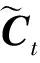
2 变形趋势综合分析方法

结合各方法的优势，构建一种融合卡尔曼滤波、分形理论和LSTM模型的大坝变形趋势综合分析方法，其流程如下：

步骤1利用卡尔曼滤波削减原始观测数据中的干扰和噪声，即滤波处理。

步骤2基于滤波处理后的数据，通过R/S分析法，分析判断大坝变形序列的发展趋势，对大坝未来变形进行初步的定性判断。

步骤3基于滤波处理后的数据构建LSTM模型，进一步对大坝未来变形进行定量分析判断；同时，引入其他神经网络预测模型，以验证LSTM模型的有效性和优越性。

步骤4将LSTM模型的预测结果同R/S分析法的分析判断结果进行对比分析，通过R/S分析方法和LSTM二者的结合，在定性的基础上加入定量元素，共同评价大坝未来的变形情况。

3 实例分析

以某混凝土重力坝为例，对该坝某测点处未来变形趋势进行分析评价。大坝共布置了12个引张线测点，以实现对坝顶水平位移情况的监测。本文选取位于10号坝段的引张线测点EX8从2013年8月10日至2014年12月22日的位移观测值用于分析，共计500个数据，其过程线见图1中黑色曲线。

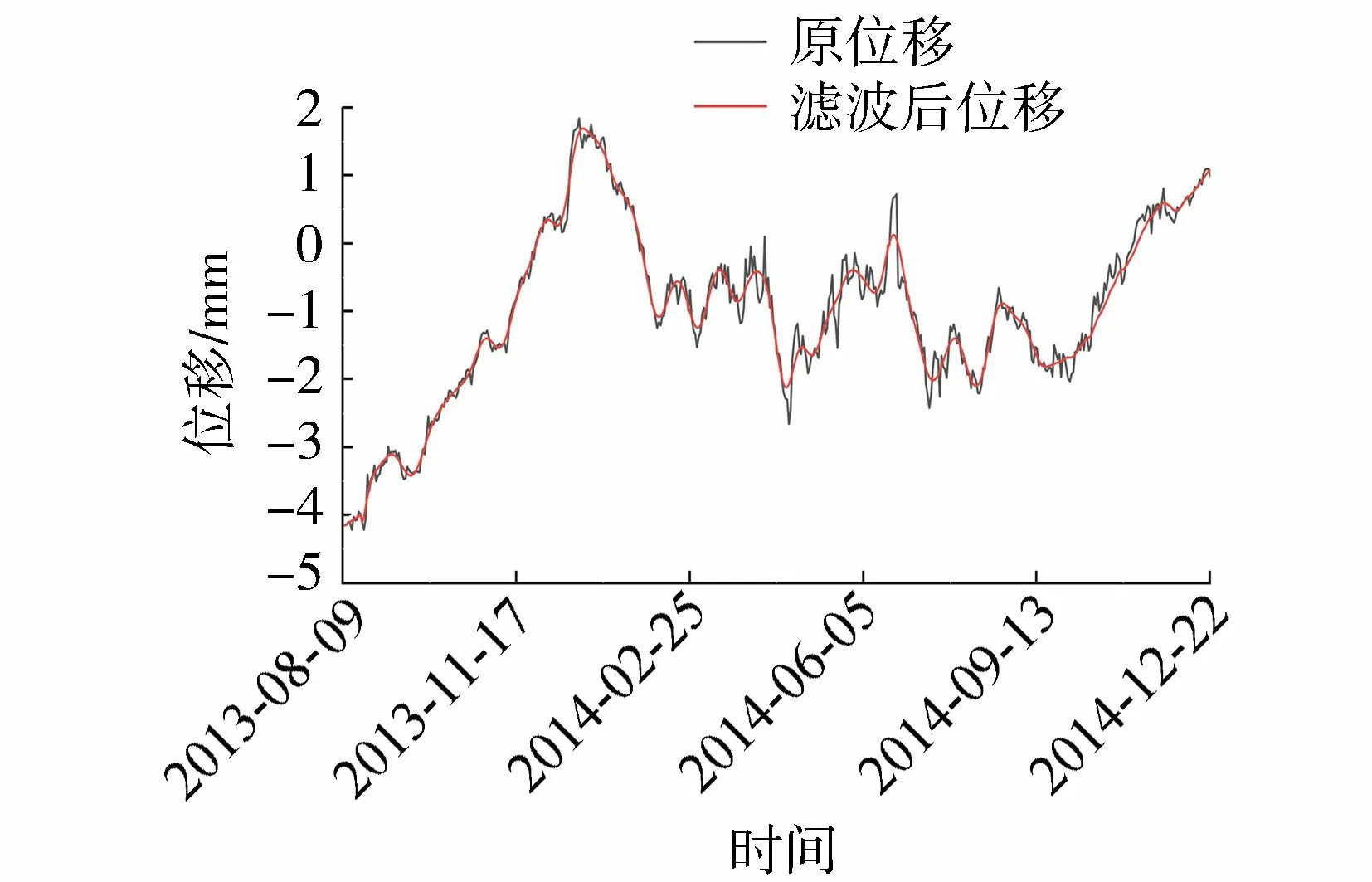
图1 位移过程线

3.1 卡尔曼滤波处理

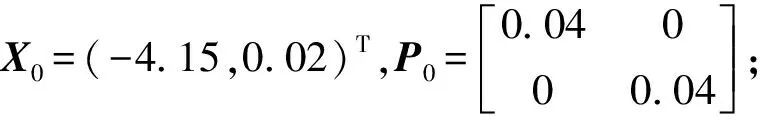
由图1可见，滤波值所呈现的位移变化规律同实际测得的位移值变化规律基本一致，且滤波后位移过程线一定程度上剔除了原位移过程线中由干扰和噪声产生的起伏和扰动，更加平滑，降低了粗糙程度，增强了位移监测数据的趋势性特征，更加趋于真实。滤波值和原始位移值之间的残差大部分在±0.1 mm以内，说明卡尔曼滤波处理有一定的数据平滑效果，在削减噪声影响方面效果明显[18]。

3.2 大坝变形R/S分析

在卡尔曼滤波处理的基础上，为初步定性分析大坝变形序列的发展趋势，基于2014年10月1日之前的417个大坝变形数据，根据R/S分析法对大坝变形趋势进行分析评价。具体操作流程如下：将时间序列划分为m组互不重叠的子序列，分别计算求得每组子序列的R/S统计量，再求其均值，进而得到对应不同长度n的平均(R/S)n值，分别对n值和(R/S)n值求对数，之后以lgn作为横坐标、lg(R/S)n为纵坐标绘制lg(R/S)n-lgn双对数坐标散点图，再通过最小二乘法对散点进行线性拟合，得到的直线斜率即是Hurst指数H；类似地，可绘制lgVn-lgn双对数坐标散点图进行辅助分析。R/S分析结果如图2所示。

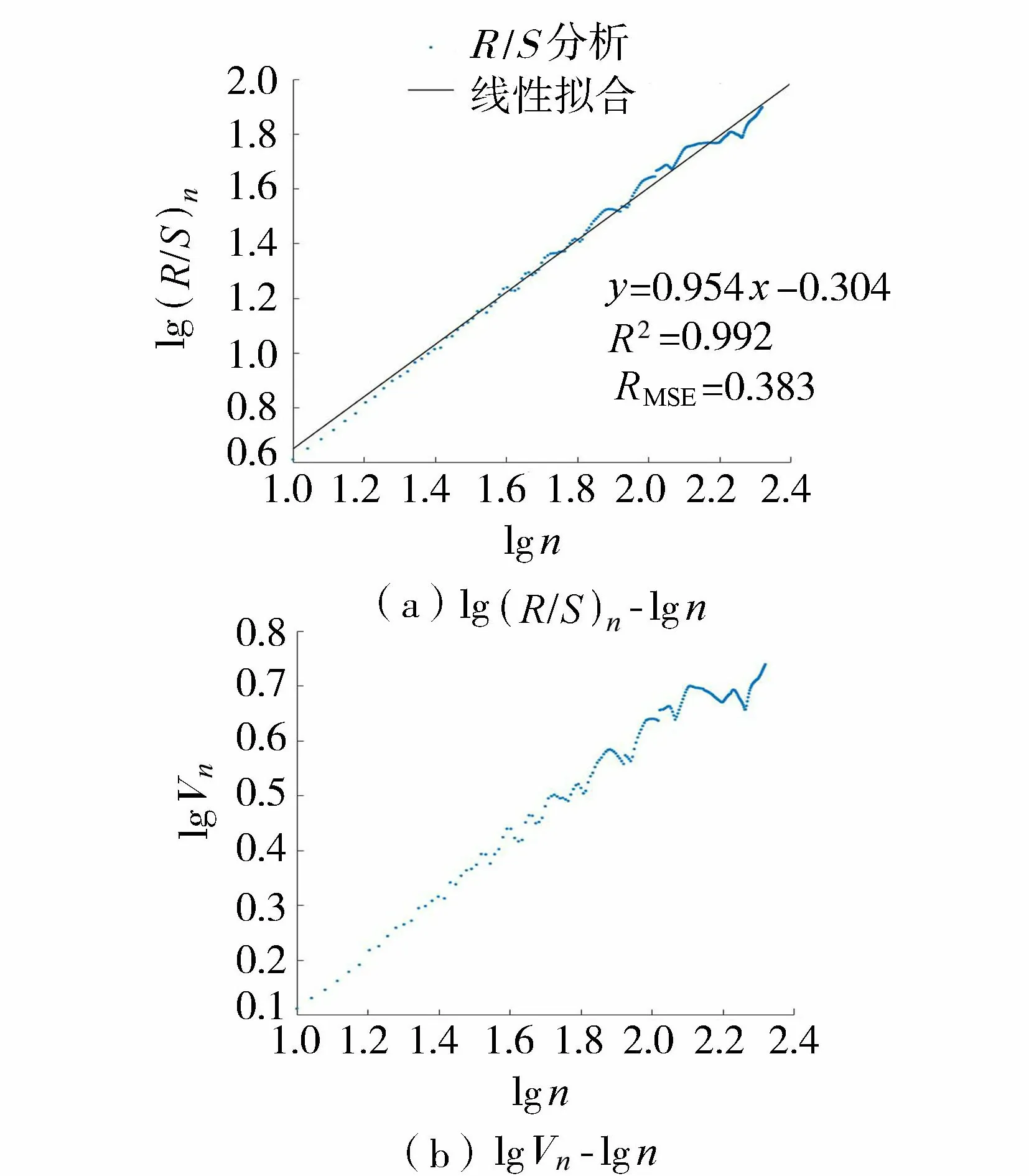
图2 大坝变形R/S分析结果

由图2(a)可见，lg(R/S)n-lgn双对数坐标散点图除局部存在小幅波动以外总体上呈线性趋势，说明此变形序列存在部分随机性的同时趋势性较为明显。通过线性拟合得到的均方根误差RMSE为0.383 mm，相关系数为0.992，均方根误差较小，拟合度较高，表明分形分析结果具有较高的可信度和不错的参考价值，同时求得此大坝变形序列的Hurst指数H为0.954，大于0.5，表明该测点处的大坝变形趋势呈现正向持续增长性，且H较为靠近1，加之lgVn-lgn双对数坐标散点图总体呈上升趋势，说明大坝该测点处变形监测序列存在显著的长程相关性，具有较强的规律性和代表性，持续性强且趋势增强明显。根据H可得分形维数D为1.046，略大于1，可知大坝该测点处变形以线弹性为主，兼具部分非线性特征。结合上述分析，可初步推断大坝该测点处变形较为稳定。

综上所述，可初步判断出未来一段时间内大坝该测点处变形存在较强的持续增长性特征，变形值会随着前期的增大而继续增大，且变形变化较为稳定。

3.3 LSTM建模预测

将经过卡尔曼滤波处理过后的500个数据中2014年10月1日之前的417个数据用于LSTM建模，后83个数据用于模型预测验证，利用MATLAB进行LSTM模型的构建。参数寻优采用Adam算法，训练时点数设置为40，隐含层节点数设置为20，窗口长度设置为20，其余参数则采用默认值。

为验证LSTM神经网络在大坝变形预测中的优越性，在同样数据的基础上建立BP神经网络模型和ELMAN神经网络模型，对未来变形值进行分析预测。由于模型预测精度与网络隐含层节点数之间关系密切，本文采用试算法拟定隐含层节点数，最终确定BP神经网络和ELMAN神经网络的隐含层节点数分别为12和3。各模型预测过程线如图3所示。

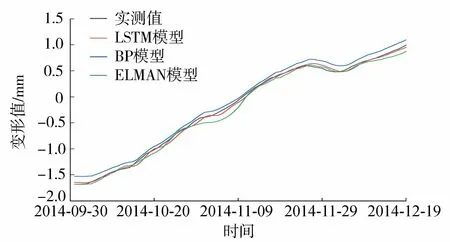
图3 各神经网络模型的预测过程线

由图3可以看出，LSTM模型、BP模型和ELMAN模型的预测过程线与实测值过程线均较为贴合，均方根误差均较低，分别为0.0367 mm、0.0899 mm和0.0695 mm，预测结果较为理想，综合3.1节的论述，分析其原因不难得出：本文在原始数据的基础上加入了卡尔曼滤波进行降噪处理，一定程度上削弱了干扰和噪声的影响，平滑或剔除了不合理的波动，使数据的趋势性特征得以保留和强化，信息表达的真实性和稳定性增加，进而使得模型的学习拟合过程更加趋于简单化和高效化，降低了模型预测结果的不确定性，保证了预测精度，一定程度上验证了对原始数据进行卡尔曼滤波降噪的可行性和必要性。

对比3种模型的预测效果，相较于BP模型和ELMAN模型，LSTM模型的预测过程线同实测过程线更为吻合，其预测值的变化规律与实测值更加趋同；LSTM模型预测结果的均方根误差最小，预测精度更高。因此相较于其他神经网络模型，LSTM神经网络模型预测效果更为理想，能更为稳定地反映大坝变形的趋势和规律，在大坝变形预测中更为适用。

由图3的预测结果可见，大坝该测点处变形在约90 d内始终保持一种稳定的正向增长的态势，呈现出较强的持续增长性特征。

3.4 变形趋势综合分析

将LSTM模型的定量预测结果同R/S分析法的定性分析结果进行对比，实现对彼此预测判断结果准确性的相互检验，可见二者均判断得到该测点处的大坝变形存在正向持续增长的趋势，综合分析结果与工程实际情况相符。这既在一定程度上说明了R/S分析法的定性分析评定结果的有效性，又验证了LSTM模型定量分析判断结果的可靠性，同时也证明了本文将R/S分析法用于大坝变形趋势定性层面的分析，再将LSTM模型用于大坝变形趋势定量层面的评判，层层深入、互为佐证的大坝变形趋势综合分析方法思路的可行性和有效性。

4 结 语

本文融合卡尔曼滤波、分形理论和LSTM模型三者的优势，提出了一种大坝变形趋势综合分析方法。实例分析结果表明，卡尔曼滤波能一定程度地削减大坝变形监测数据中的干扰和噪声，提升大坝变形趋势分析的合理性和可靠性；基于卡尔曼滤波的降噪处理，分形理论和LSTM模型均能较为准确地对大坝变形趋势分别进行定性分析评价和定量预测判断，有效克服了大坝变形监测数据普遍存在的随机性和非平稳性等问题；融合分形理论和LSTM模型的定性和定量分析结果，可实现大坝变形趋势的综合评判，相较于单方面的定性或定量预报，可靠度得到了更好的保障。可见，本文提出的大坝变形趋势综合分析方法具有一定的适用性和推广价值。