粗大误差剔除在反应堆功率计算中优缺点分析

康凯强，吕杰帅，邱宪苗，谢岱良

（广西防城港核电有限公司，广西防城港 538001）

0 引言

国内主流的压水堆核电站反应堆功率常采用一二回路热平衡法计算，计算过程参考标准NB/T 20195—2012 执行[1]。在数据采集时使用3σ 粗大剔除方法进行坏值剔除[2]，当剔除率小于5%时认为数据可用。但此判定方法在某些工况下有一定缺陷，不能完全反应系统正常，本文通过模拟计算以及对某核电厂实际运行案例分析，讨论坏值粗大剔除方法在核电厂反应堆功率计算中的不足及应对措施建议。在工程应用时，参考本文建议可以提前判定系统是否正常，提高热平衡计算结果的准确性。

1 压水堆核电站堆芯热功率测量规程

压水堆核电厂采用热平衡试验的方法进行反应堆功率测量，由KME 系统（试验仪表系统）执行，热平衡试验是根据平衡原理，蒸汽发生器二回路热量应与一回路热量相等，通过计算二回路热量反推一回路热量（图1）。

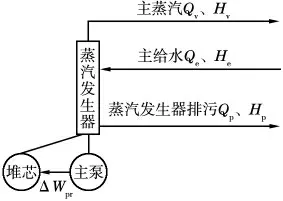
图1 热平衡基本原理

利用热平衡试验计算反应堆堆芯功率的计算原理如下：

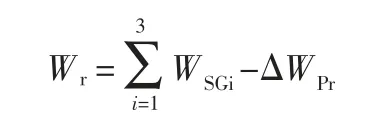
式中，Wr为反应堆堆芯的功率，WSGi是每个蒸汽发生器提供的热功率（i=3），WPr是除了反应堆堆芯产生的热功率以外其他方面输入到一回路反应堆冷却剂的热量。

为满足上述计算，现场使用孔板测量给水压差（用于计算给水流量）、给水压力、给水温度、蒸汽压力等初始参数。

2 KME 系统坏值剔除简介

对一组数据进行测量时误差包含随机误差、系统误差和粗大误差，为减小其对测量结果的影响，采取的措施有：对于随机误差，一般在测量系统中无法消除；对于系统误差，只要其满足测量者的需求，也一般认为可以接受，而对于粗大误差由于其不确定性需要对其剔除。

粗大误差的剔除方式有很多种，KME 系统剔除的方式采用3σ 准则（Pauta criterion），即认为在所取样本中样本数值在平均值±3σ 内的数据为随机误差，超过3σ 的数据为粗大误差，应予以剔除[2-4]。

KME 系统在剔除过程中又采用了循环剔除方式[5]，其剔除逻辑见图2。

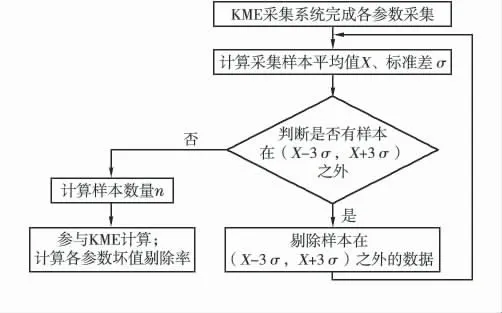
图2 KME 系统坏值剔除逻辑

3 KME 系统坏值粗大剔除方式分析

3.1 系统状态稳定时坏值粗大剔除对热功率的影响

从系统自身波动来说，KME 系统所有的信号对时间满足余弦分布，即其本身存在波动规律。以给水流量信号为例，稳定工况下给水流量测量压差信号如图3 所示。

从图3 可以看出信号分布φ=Acos（wt+a）+b 的时间规律，当波动周期远远小于0.2T，且一个周期内采集数据大于10 个时，其标准差的积分公式为。因为m 为正整数，则，

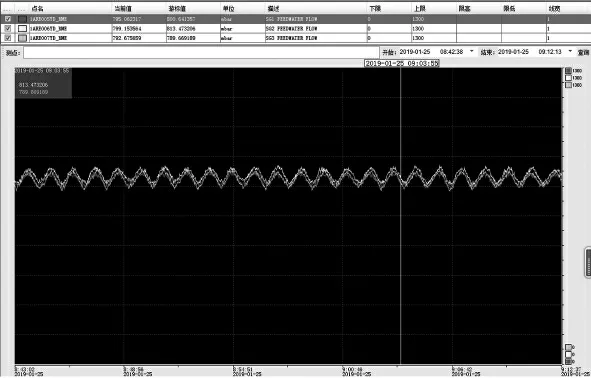
图3 某核电厂给水流量信号随时间波动情况

可以看出3σ＞A，即系统稳定时数据采集的正常波动被包络在该准则内，不产生剔除数据。

3.2 机组正常升降功率时坏值粗大剔除对热功率的影响

当机组处于升降功率时，需要在原有信号上叠加一个一次信号φ=kt+c，即原信号变为φ=Acos（wt+a）+d+kt，其标准差的积分形式推导如下：

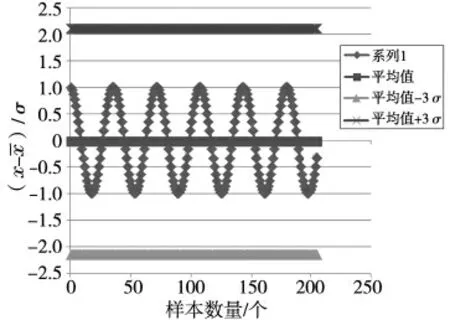
图4 正常型号数据采集的坏值剔除情况

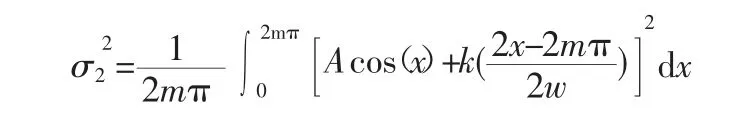
将积分式内部拆分为二项式，则有

可以看出，3σ2与A 和k 值有关，但与采样时长有关，当采样时长T 一定时，k 绝对值越大整个信号越趋近于一条直线上，

当k 趋近于0，整体信号约趋近于余弦函数，其标准差也变为

从图5 可知，对于上升阶段的信号采集，所有信号均包络在3σ 范围内，如果采用3σ 准则不产生坏值剔除。

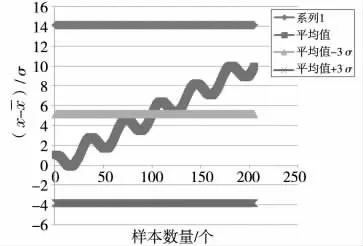
图5 信号以一定速率上升时的坏值剔除情况

西南某核电站CPR1000 机组某次机组降功率期间KME 系统计算报表如图6 所示。即采用3σ 准则的坏值剔除方法在核电站KME 系统热平衡计算过程中，坏值剔除率无法用来表征系统升降功率过程中的稳定性。

图6 某次降功率期间KME 系统反应堆热功率计算报表

3.3 当系统产生阶跃信号时坏值粗大剔除对热功率的影响

本文只讨论系统中单一异常情况，并假设异常波对机组运行参数影响较小，因此不考虑系统的阻尼作用（主要来源为反应堆的功率、温度等负因素），可认为系统为一阶响应。图7 为模拟的应曲线，其与西南某核某次给水温度数据产生的阶跃曲线非常近似（图8）。

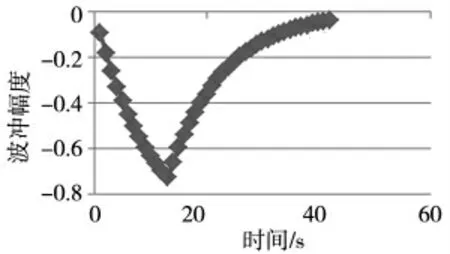
图7 脉冲信号的一阶响应

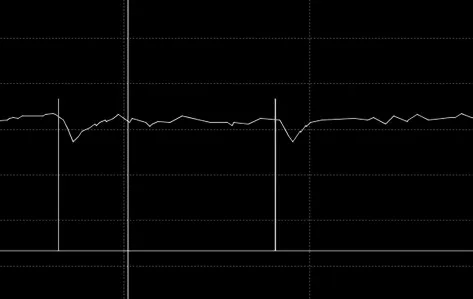
图8 给水温度信号阶跃曲线

在一个周期内系统对于脉冲信号的一阶响应函数为[3]：

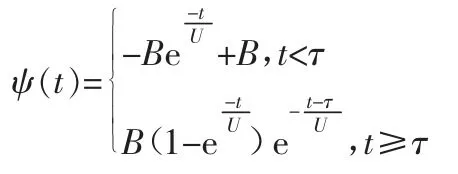
其中U 为系统的响应时间。

采集信号的时域函数为：

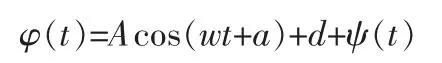
假设在整个试验周期内出现n 次脉冲，脉冲次数有限，次数应规定在1～3 次，类似于上文提到的主给水温度信号阶跃。此时可以发现T 远远大于τ，则其积分形式表示标准差为，则

从数据上看，整体脉冲最大值出现在τ 时间中，最大值为φ（τ）=，当φ（τ）=时系统肯定不会出现坏值剔除率。此时B/A≥0.89。

脉冲信号不强，在系统上无法识别，无论如何不产生坏值剔除率；

当B/A<0.89 时，坏值剔除产生数量与系统产生脉冲信号的时间、脉冲信号持续的时间和系统响应时间比值τ/U 有关。

从图9 可知：①τ/U 越大，产生的坏值剔除数量越多，即脉冲存在的时间越长，坏值剔除越多；②B/A 越小出现坏值剔除的τ/U 越大，当B/A 小于2.12 时，无论τ/U 多大、均不可能出现坏值剔除率，说明脉冲信号越大，越容易产生坏值剔除；③系统变动曲线线形只与τ/U 有关，τ/U 越大、系统恢复至原基准所需时间越短。其中，图9 未考虑脉冲尖峰与系统本身波动的情况，如需考虑则需要在坏值的限值加正负1A 即可。

图9 B/A 为5、3、8 时坏值剔除与τ/U 的情况

根据上文提到的脉冲信号的一阶响应函数，产生坏值剔除的时间不等式为

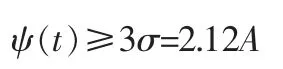
解上述不等式得到：

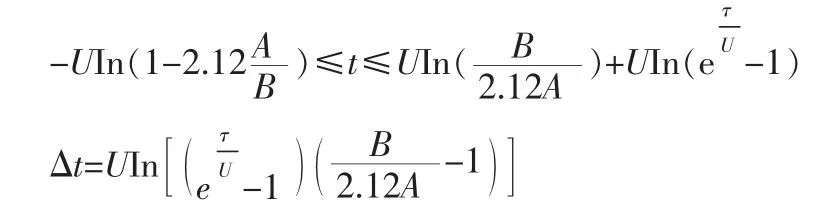
在该脉冲周期的坏值剔除率可以表示为η=Δt/T，利用MATLAB 绘制的η—τ/U、B/A 关系三维MAP 图（图10）。

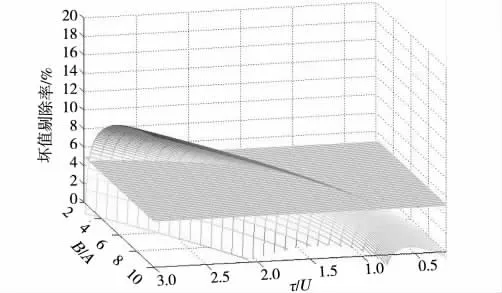
图10 坏值剔除率与τ/U 和B/A 的关系

推广到整个采样周期中，则η=nΔt/T。

西南某核电厂某次给水温度信号阶跃产生的坏值剔除率情况如图11 所示：给水温度信号脉冲产生的周期为20～30 min，与KME 系统采集周期基本一致（KME 系统数据采集周期为20 min），即n=1；脉冲τ 时间存在为73 s，即经过73 s，给水温度信号到达极值；此后系统温度开始恢复正常，经过约103 s 后温度恢复至基准温度。

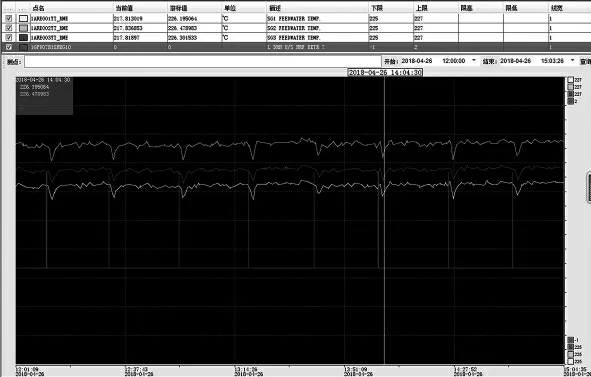
图11 某核电厂给水温度信号阶跃情况

从图9 可知，系统变动曲线情况得出τ/U 应该在1.7～2.0；该时间段内给水温度的标准差约为0.02 ℃，计算得到波动的幅值A 为0.028 ℃；截取数据得到当时间为73 s 时，温度比平均温度（基准温度）下降约0.08 ℃；将上述数据代入脉冲信号的一阶响应函数公式，可以得到B/A 为3.4～3.6；再将上述数据代入总剔除时间的计算中得到Δt 为80～90 s，将其代入1200 s 的采数区间可以得到坏值剔除率在7%～8%。

4 结论与建议

（1）采用3σ 准则方法对KME 系统计算数据进行坏值剔除：①当热力系统稳定时，不会产生坏值剔除；②当热力系统正常升降功率时，不会产生坏值剔除；③当热力系统中产生持续时间较长、信号幅度较大的脉冲信号，将会产生坏值剔除，而这些信号很有可能反应热力系统中存在异常。即采用3σ 准则方法对KME 系统计算数据进行剔除时，剔除率在表征热力系统稳定性方面有一定缺陷，无法表征热力系统是否在进行升降功率。但对计算数据进行坏值剔除又是必要的，其能够指导试验工程师及时快速地发现热力系统中可能存在的异常。

（2）CPR1000 机组在使用热平衡方法进行反应堆功率计算时，应人为验证系统是否处于稳定状态，避免试验在升降功率期间进行。