铁路5T 设备的可靠性预测模型及验证

潘 磊，陈佳豪，王 宇

（1.中国铁路西安局集团有限公司，陕西西安 710054；2.西安交通大学机械工程学院，陕西西安 710049）

0 引言

铁路车辆运行安全监控系统（简称“5T 系统”），包含THDS、TPDS、TFDS、TADS、TCDS[1]，是我国用于保障列车运行安全的重要手段。通过集成先进的检测、通信及信息处理技术，5T 设备可实现对过往车辆的动态监测，是提早发现列车故障的有效利器。5T 设备的广泛应用，大大降低了列检人员的工作量，提高了列检工作效率与准确率，为列检作业带来革命性的变革，从而保障了铁路货车的安全运输[2-6]。但是，铁路部门基本采用定期巡检的方式对5T 设备运行维护[7]，检修成本较高、效率低，无法有效保障5T 设备的平稳运行。因此，需要合理安排设备检修周期，减少设备故障率，提高列车通过运行效率[8]。通过基于设备历史故障发生时间建立一个可靠性分析模型，对当前5T 系统的合理维护具有重要意义。

本文基于西安某铁路公司统计的铁路5T 设备故障记录数据，通过将数据清洗筛选出100 余个有效样本，并利用AMSAA模型对其进行拟合、预测以及分析其可靠性变化趋势，为检修制度转变提供理论支撑，也为其向状态修的转变提供了一个思考方向。

1 AMSAA 模型

1972 年至1988 年期间，美军AMSAA（Army Material System Analysis Activity，装备系统分析中心）提出了用于设备可靠性的AMSAA 模型[9]，同时，其也给出了模型参数的极大似然估计估计公式、MTBF（Mean Time Between Failure，平均无故障时间）、瞬时故障率等计算方法。

（1）模型通过假设一个可维修系统在的时间区间内发生的故障次数服从一个非时齐泊松过程，即：

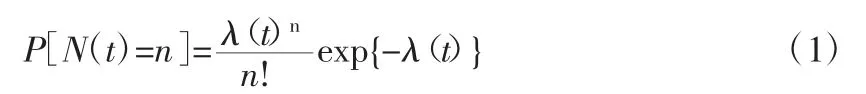
式中 P——事件发生的概率

N（t）——在内发生的故障次数

n——故障累计次数

λ（t）——故障均值函数，即在区间（0，t）上故障发生次数的数学期望

由此可得，其瞬时故障强度可以表示为v（t）=dE［N（t）］/dt。它表示在单位时间内设备发生故障次数的期望值或理论平均值。在非时齐泊松过程中，故障关于时间的均值函数以及故障强度函数分别被定义为

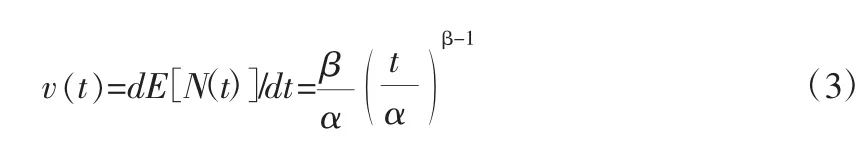
式中 α——模型的尺度参数

β——模型的形状参数

（2）根据泊松过程具有的独立增量性以及该模型的定义，可计算在区间上n 次故障发生的概率为：

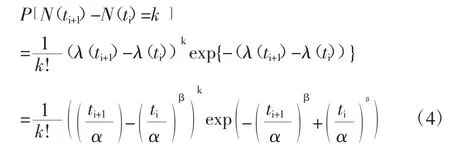
式中 ti——第i 个故障记录时间点

ti+1——第i+1 个故障记录时间点。

可求得设备到达时刻tn时的MTBF：

（3）可以求出服从非时齐泊松过程模型的设备在前k 次故障发生时间段0=t0＜t1＜…＜tk≤T 的联合概率密度函数为：

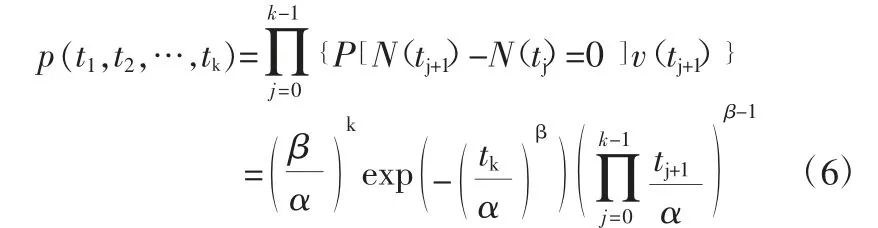
其中，假设N（t0）=0，同时］可以表示为在时间间隔ti+1与ti之间发生故障次数为0 的概率，乘以v（ti+1）则表示在ti+1处发生一次故障，再将其各部分相乘表示其联合概率密度。

通过对式（6）中t1，t2，…，tk-1的积分，可求得第k 次故障发生时刻的概率密度函数，从而有助于确定出设备的检修时刻。其故障发生时刻的概率密度函数为：

式中 Γ（k）——Gamma 函数

k——故障次数

基于联合概率密度函数的期望公式，不难得出第k 次故障的发生时间的估计值。

由于以上式子需要求解模型参数才能得到结果，参数的求解可依据式（6）进行求对数似然得到结果：

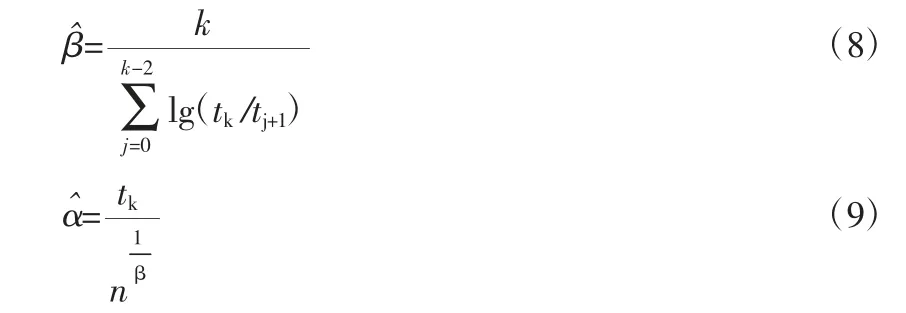
同时也可根据定义求出其无偏估计值：

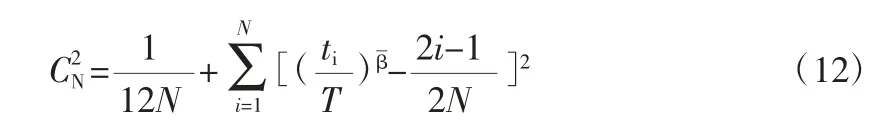
其中，N=k-1，设定显著度a，根据可靠性手册查找克莱默—冯·梅赛斯临界值。若则认为满足要求。

（5）为更好地基于数据分析设备的可靠性，可通过第k 次故障达到时间及其之前的故障到达时间计算趋势统计量ω：

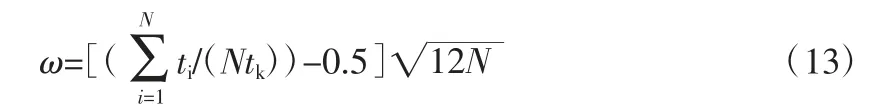
其中，tk表示第k 次故障到达时刻，N=k-1。

（6）由于工程实际中维修更关注在提前预防性维修，该模型还可提供基于当前（k）次故障发生时间与选定置信度求解故障发生时间的区间下限值：

2 设备退化过程评估及计算流程

2.1 设备的退化阶段

如图1 所示，由多个不同零部件组成的复杂设备的故障强度变化规律，通常采用浴盆曲线进行描述[10]。这样设备的全寿命周期（也称“全寿命退化过程”）可以分为以下3 个阶段：

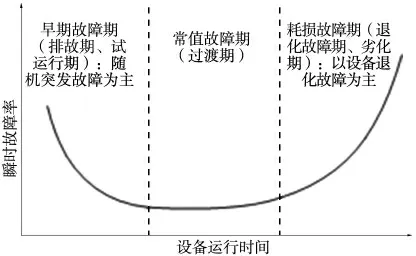
图1 设备寿命浴盆曲线

（1）早期故障期，也被称为排故期、试运行期。该阶段中，故障间隔时间短、故障发生频次高，故障类型以随机、突发故障为主。

（2）过渡区或常值故障期，在早期故障期末尾，故障强度逐渐降低，接近于常数，所以这一阶段有时也被称为常值故障期。但是，诸多设备并不存在明显的常值故障期，只存在一个从早期故障到耗损故障的过渡阶段[10]。并且，由于设备不同，过渡阶段的长度也各有差异。

（3）耗损故障期，这个阶段也被称为退化故障期、劣化期[10-11]。随着时间的推移，设备的各个零部件会不可避免地耗损和老化，这导致设备中的故障原因逐渐从由随机突发故障占主导，向退化故障（如疲劳断裂、磨损、老化、点蚀等）占主导转变。

2.2 计算流程

综合考虑模型对数据的适用情况、可靠性分析目的计算如下：

（1）输入各故障发生时间并排序。

（2）从第1 次起，通过与第1 次故障发生时间差分得到故障基准时间，并设置第1 次故障时间为0。

（3）从第2 次故障起，利用得到的数据进行拟合优度的计算。

（4）如果满足适用性条件，计算模型参数、各次MTBF 值、瞬时故障率以及预测故障区间下限值。

（5）利用最小二乘法拟合MTBF，以此判断设备的可靠性趋势。

3 应用案例

该项目数据由我国某铁路公司，从数据库调取2015 年4 月至2020 年5 月的某铁路段故障记录数据（精确到分）。考虑5T设备的复杂工况及当前设备已具有的辅助维修功能，将非元器件失效造成的故障记录删除，同时涉及的时间跨度很大，因此以“天”为时间单位。采用选择的AMSAA 模型进行设备的可靠性分析，计算过程如下。

3.1 5T 全网路设备模型应用

进数据筛选及清洗，可得到177 条故障记录，将第一条故障发生时间当作计时起始点，可得到故障记录数据，由于涉及数据过多，仅展示前2～31 次（第一次为0）故障记录（表1）：

根据上文列举流程，计算出模型拟合结果及偏差、预测下限和偏差以及MTBF 与故障率。其中，图2～图5 给出了AMSAA模型拟合故障记录的结果、预测结果及局部放大图和偏差计算图，图6、图7 中散点为设备MTBF 计算结果和瞬时故障率计算结果，曲线为其二次拟合曲线。

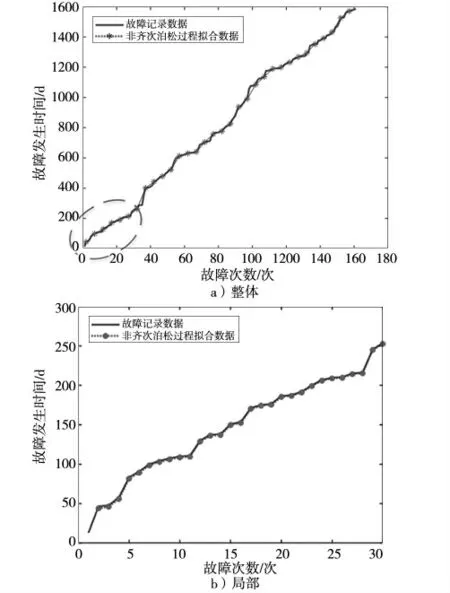
图2 模型拟合故障记录

3.2 结果分析

从图3 可以看出，AMSAA 模型可以很好地拟合5T 设备的故障记录。随着输入的故障数据增多，模型对故障记录数据拟合的情况越好。图5 反映了模型对设备故障的预测下限值，可出看出其值均在真实故障发生前。虽然模型的预测偏差计算结果有一定波动，但平均偏差较小。经分析，产生波动的主要原因在于，受环境等其他因素干扰，设备间的故障到达时间并不稳定，且不同设备间存在一定的工况差异，后续研究还需融入环境因素建立更复杂模型。图6、图7 反映了设备可靠性变化趋势，不难发现，随着时间的增加设备的可靠性有一定上升，散点图可看出当前设备可靠性稳定在一定区间并进行波动。同时其结果反映，检修间隔的增长并不会造成设备可靠性的下降。因此，可通过试点的方式、采取延长检修间隔的巡检措施，减小设备巡检的压力。

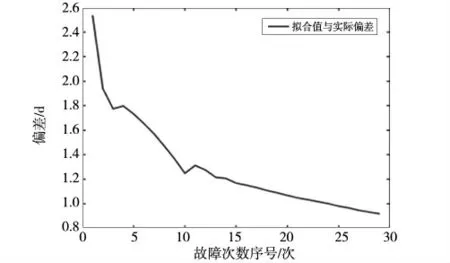
图3 模型拟合故障记录偏差结果

图4 模型故障预测结果

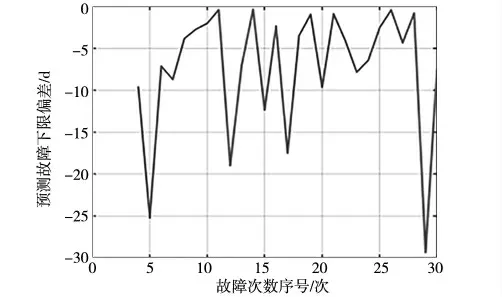
图5 模型故障预测偏差结果

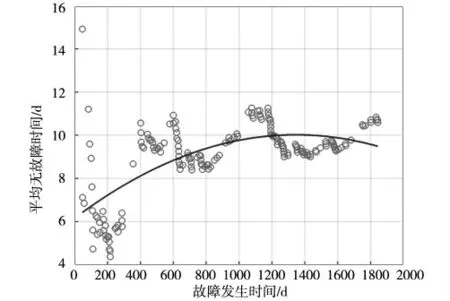
图6 设备MTBF 计算结果

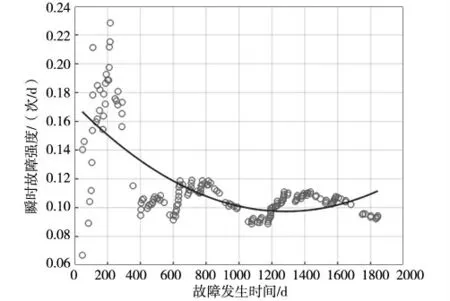
图7 设备瞬时故障率计算结果

4 结束语

AMSAA 模型可以很好地拟合铁路安全监测设备的故障，并对其进行可靠性的动态分析。通过MTBF 计算及拟合结果可以分析出设备可靠性的变化趋势，并作为设备进行检修计划的调整以及大修、更换的理论依据。从当前预测结果可看出，预测结果不够稳定，仍存在一定偏差与波动。后期需要进一步对各站点加装环境监测的传感器，通过深度挖掘设备工作环境中的信息，建立一个复合动态模型，实现对设备故障发生时间的准确、稳定预测。同时，融合设备运行状态的监测信息，通过将其算法融入当前带有远程监测、控制的设备健康管理系统，实现5T 设备检修方式从设定固定检修周期向基于监测状态执行维修的转变，实现铁路设备维修的“少上线、精上线”目标。