基于空间电荷输运特性的电缆附件界面位置确定方法

程若曦, 高 颖, 王 翔

(1. 山东理工大学， 山东 淄博 255000； 2. 国网山东省电力公司日照供电公司，山东 日照 276800 3. 中国科学院过程工程研究所多相复杂系统国家实验室， 北京 100190)

0 引 言

高压直流(High Voltage Direct Current, HVDC)电缆因低损耗、高可靠性以及便于维修等优点被广泛应用于远距离电力传输。然而由于电缆材料在制备或使用的过程中容易存在物理或化学缺陷，电荷在由缺陷形成的陷阱中积累，容易引起电场畸变、绝缘老化等问题，甚至导致绝缘击穿[1-2]，因此，高压直流电缆存在电荷积累问题[3-4]。与单层电缆不同，双层电缆附件使用复合绝缘材料。由于其复合界面两侧具有不同的电学性能，界面位置处更容易积累空间电荷，绝缘击穿和故障也大多从此处开始发展[5]。因此，复合绝缘材料对空间电荷调制的重要性逐渐显现。

目前，国内外学者大多通过聚合物分子结构改性、纳米材料掺杂以及改善电极材料性质等方法来对绝缘材料空间电荷调控进行研究。文献[6]基于分子链动力学对传统双极性电荷输运模型进行改进，探讨深陷阱能级变化对电缆接头绝缘界面电荷分布的影响。研究表明深陷阱能级增大，导致电荷在介质内部的扩散和迁移受到阻碍，大量电荷在界面积聚。文献[7]通过表面分子调控降低了聚合物深陷阱的密度，该方法对于空间电荷的抑制作用效果显著。文献[8]对不同低密度聚乙烯(Low Density Polyethylene，LDPE)含量的聚丙烯(Polypropylene，PP)复合材料的电学性能进行了研究。结果表明LDPE改变了PP的微观结构，在LDPE含量为40%的共混体系中，空间电荷明显受到抑制。文献[9]通过在电缆绝缘层上制作成应力锥和附件增强绝缘层的方法，一定程度上消除界面，改善了原界面上空间电荷的积聚情况。文献[10]研究了炭黑掺杂的半导电电极对聚乙烯材料空间电荷积累的影响。结果表明炭黑含量的增大有效减小空间电荷的注入量。以上研究大多通过对电极材料的改性来实现对空间电荷的调控，而对电缆结构对空间电荷的调控研究较少。

本文以双层绝缘的直流电缆附件为研究对象，基于电荷输运机理和傅里叶定律，建立温度场和电场作用下的直流电缆径向一维轴对称模型。研究了直流电压和极性反转电压下的空间电荷在界面位置的积累特点、电场分布特性以及界面位置对绝缘层电场畸变的影响规律；进一步基于综合考虑电场畸变因子，提出一种复合绝缘界面的优化设计方法，得到对绝缘有利的最佳界面位置。研究结果可为直流电缆附件的分层设计提供理论支持。

1 双极电荷输运模型

1.1 电缆附件物理模型

图1为一维平板式样示意图。对平板式样建立物理和数学模型，对其进行微小单元层剖分，进行迭代求解。由于一维平板式样的结构特征与实际电缆模型差异较大，因此该模型不能用于研究电缆几何特点对空间电荷输运和积累特性造成的影响。

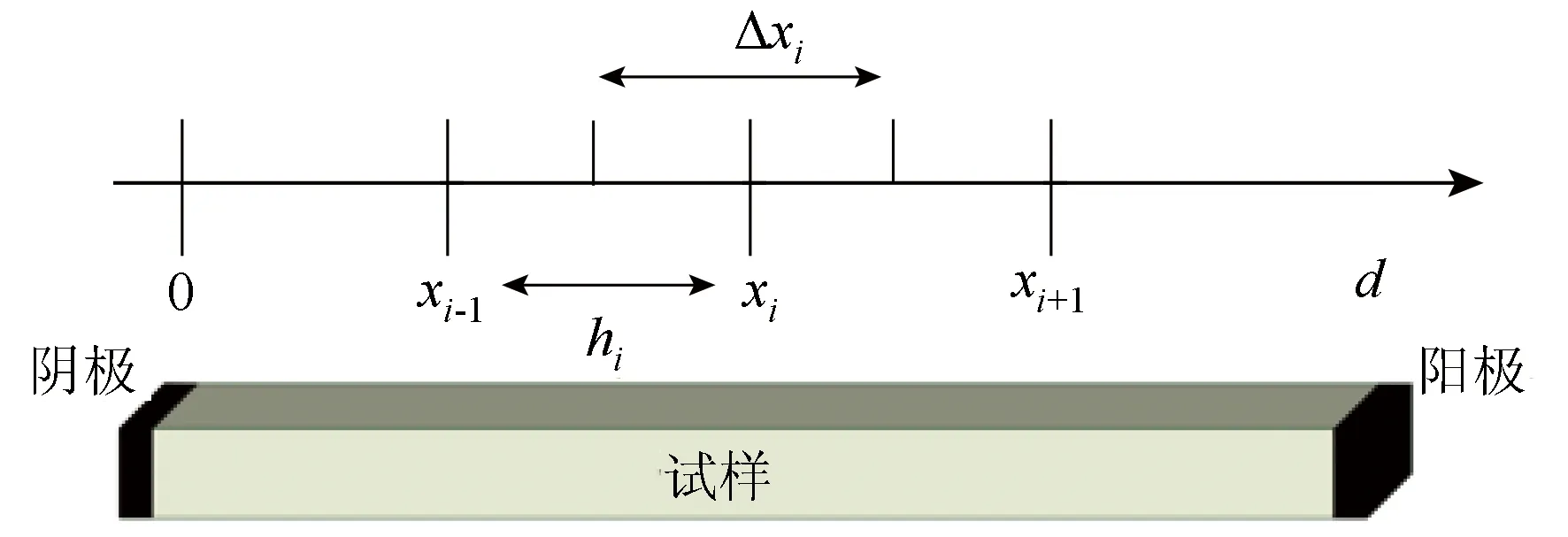
图1 平板式样剖分示意图

图2为三维电缆有限元模型。通过该模型，向缆芯施加一定直流电压，模拟实际运行情况下，电缆电场强度和温度分布，得到的切片云图如图3所示。

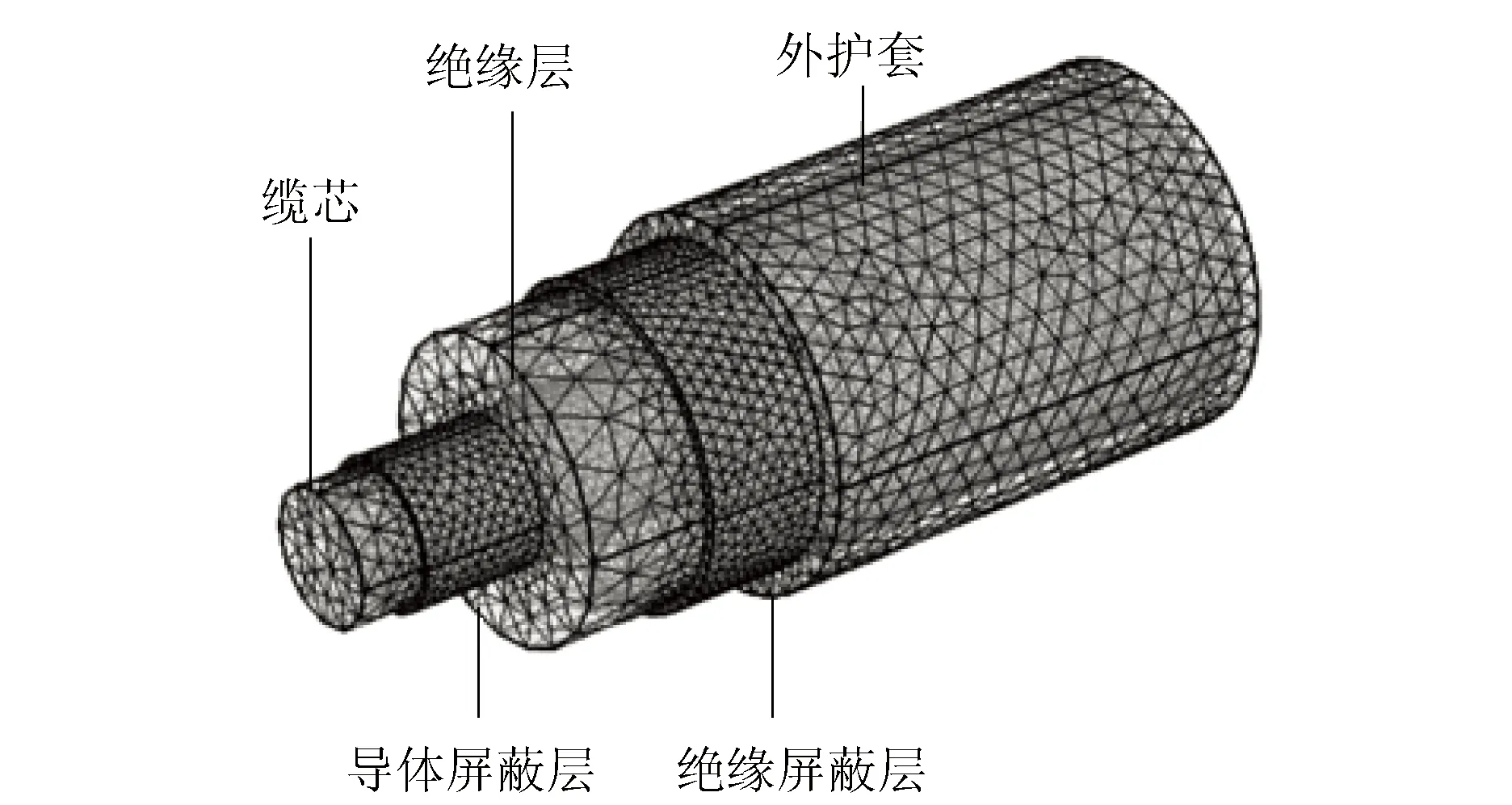
图2 三维电缆模型

图3 直流电压下电场和温度分布云图

从图3可以看出，电场和温度在电缆径向上存在梯度，且分布特性由电缆的几何特点和温度传导特性决定。由于电缆附件具有圆柱形的结构特点，因此本文研究中将三维电缆模型简化为垂直于电缆轴的二维圆形模型。更进一步将径向线段O-M绕电缆中心旋转360°形成电缆的二维圆形截面模型，如图4所示。

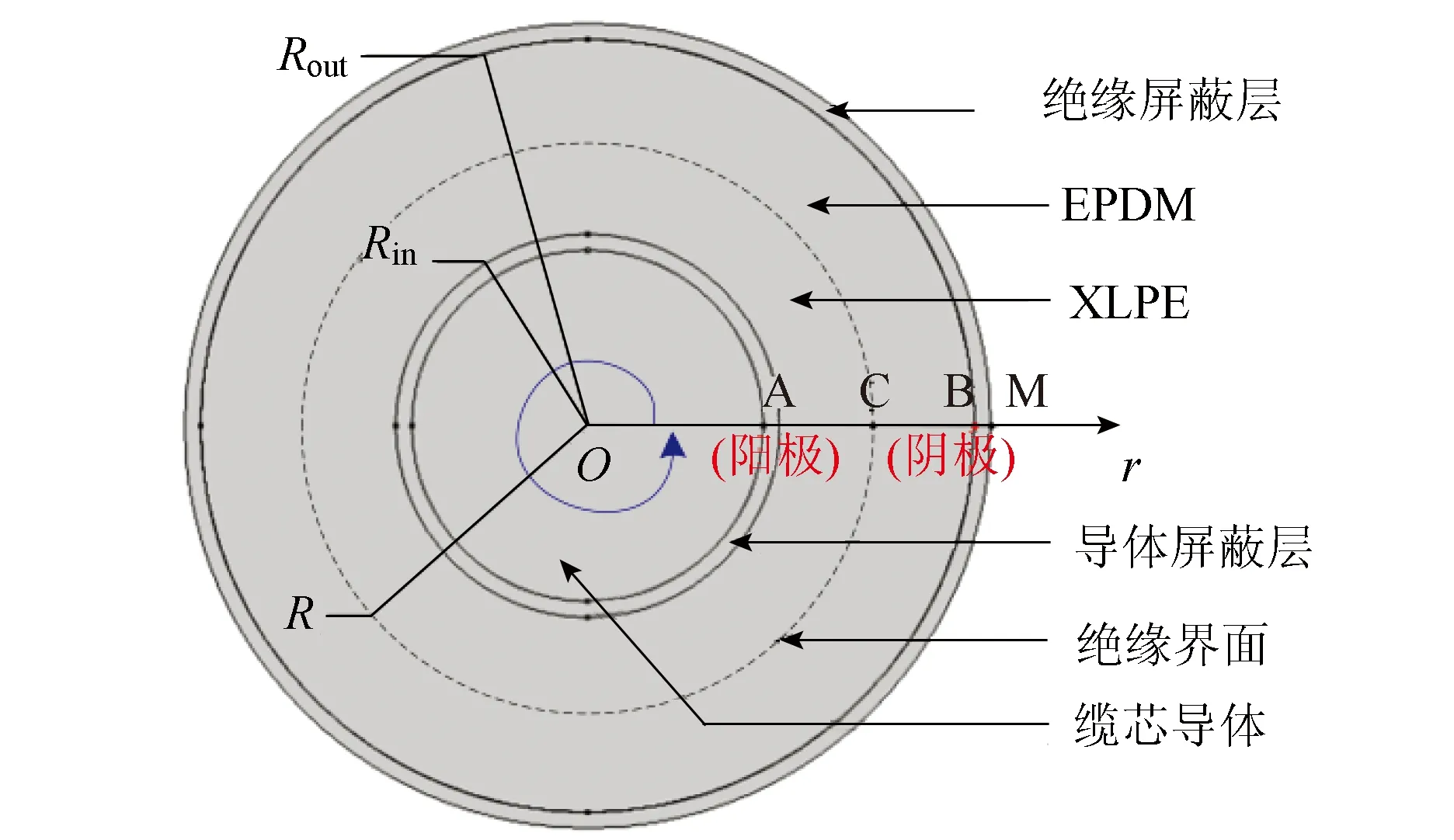
图4 仿真几何模型

其中，Rin表示绝缘层的内半径，Rout表示绝缘层的外半径，R为双层绝缘界面。本文主要讨论绝缘层线段A-C-B的空间电荷和电场分布。模拟计算中使用的相关材料参数和几何参数如表1所示。

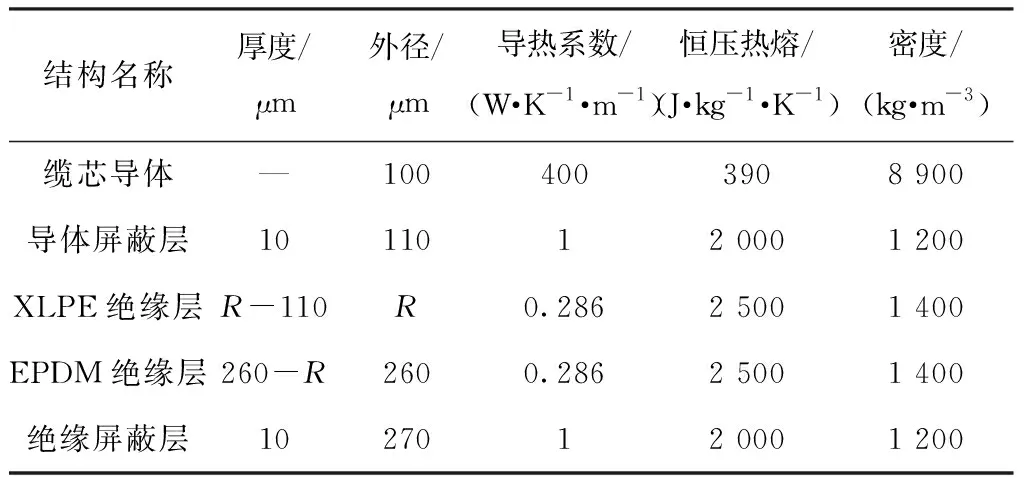
表1 电缆附件的结构参数和材料物理性质

1.2 电缆附件数学模型

双极性电荷输运原理图如图5所示。外加电压下，绝缘体与电极之间的界面处按照Schottky定律注入电子和空穴。在电场作用下，它们在导带和价带中向相反的电极移动，形成传导电流。绝缘介质的生产和运行过程中会产生化学和物理陷阱，陷阱能级位于介质的带隙中，由物理缺陷引起的浅层陷阱和由分子化学缺陷引起的深层陷阱可以捕获移动载流子并在其内部形成局部陷阱载流子。由于浅陷阱中的电荷被捕获的时间较短，交换活跃度较高，可以认为浅陷阱电荷仍然与电荷传导、介质导电有关。电荷被深陷阱捕获的时间较长，一旦入陷，需要获得足够的能量克服势垒才能逃逸，再次进入导带和价带，重新成为自由电荷[11-13]。

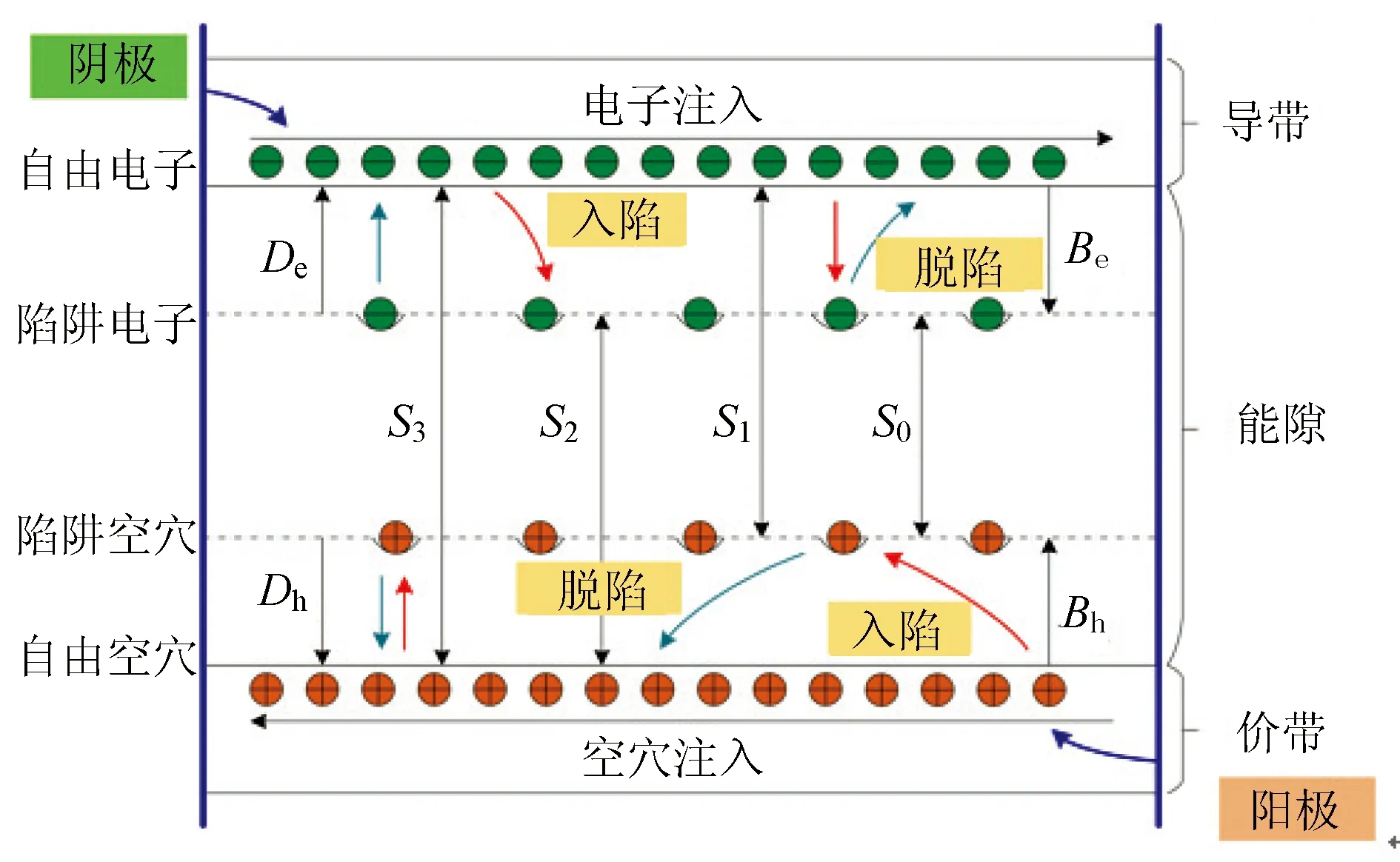
图5 双极性电荷输运模型示意图

(1)电荷注入

当外加电场大于阈值电场时，在直流电压激励下，电极将电子和空穴注入电介质，形成注入电流，可以用肖特基定律来描述[14]，即电极中的电子和空穴通过热激发克服了表面障碍，进入介质中形成自由电荷。

(1)

(2)

式中：je(Rout,t)为电子的注入电流密度；jh(Rin,t)为空穴的注入电流密度，A/m2；A=1.2×106A/(m2·K2)为理查德常数；T为材料温度，K；e为元电荷量；φie为电子的注入势垒高度；φih为空穴的注入势垒高度，eV；kB=1.38×10-23J/K为玻尔兹曼常数；E(Rout,t)为绝缘层外侧电场强度；E(Rin,t)为绝缘层内侧的电场强度，V/m；ε0=8.854×10-12A·s/(V·m)为真空介电常数；εr为相对介电常数。

(2)电荷传输

用泊松方程(3)、输运方程(4)和电流连续性方程(5)来描述电荷转移和复合。

(3)

(4)

(5)

式中：角标a为不同载流子，当a为ec时表示自由电子，et表示陷阱电子，hc表示自由空穴，ht表示陷阱空穴；j(r,t)为t时刻r位置处的电流密度，A/m2；na为表示载流子密度，C/m3，其中电子密度的符号为负；ua为迁移速度，m/s；μa为迁移率，m2/(V·s)；E(r,t)为电场强度，V/m；si为源项，表示介质中的载流子的动力反应项，包括入陷/脱陷、复合等过程，C/(m3·s)。具体来说，s1表示局部自由电子的变化率，s2表示局部陷阱电子的变化率，s3表示局部自由空穴的变化率，s4表示局部陷阱电荷的变化率。Df表示扩散系数，m2/s。

(3)电荷入陷、脱陷以及复合反应

在电荷迁移过程中，局部载流子浓度通过俘获、脱俘获和重组过程发生变化。正负极性的载流子在聚合物中相遇时会发生复合反应，将原有的两电荷湮灭，不能产生第三种载流子，因此电荷的复合会使聚合物中的电荷密度降低。

(6)

(7)

(8)

(9)

式中：s1～s4为复合反应速率，C/(m3·s)；Ne,h为电子和空穴的陷阱密度，C/m3。Be和Bh是俘获系数，De和Dh为脱俘获系数，s-1。

(4)电荷抽出

从阴极和阳极注入的电子和空穴迁移到达相反电极后，由于绝缘材料/电极之间界面势垒的阻挡，在电极附近发生异极性电荷积累。界面势垒对于电子和空穴的抽出阻挡作用由抽出系数来表征：

je(Rin,t)=Ce·μe·nec(Rin,t)·E(Rin,t)

(10)

jh(Rout,t)=Ch·μh·nhc(Rout,t)·E(Rout,t)

(11)

式中：je(Rin,t)和jh(Rout,t)分别为电子和空穴的抽出电流密度；Ce为电子的抽出系数，Ch为空穴的抽出系数，其取值为0到1之间，当其为0时，意味着完全阻挡，无任何电荷从绝缘层抽出，当其值为1时，表示完全无阻挡。

(5)欧姆热传导

导体中的电流随传输功率的变化而变化，欧姆热是由高压导体中的工作电流产生的，沿径向的热传递导致电缆截面上存在温度梯度。本文考虑了温度对电荷注入和迁移过程的影响，引入傅里叶定律来描述固体传热方程。

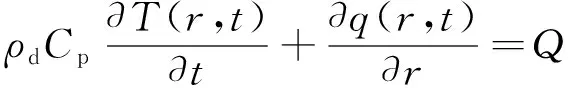
(12)

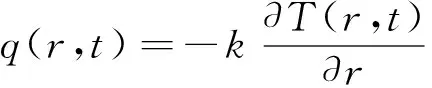
(13)

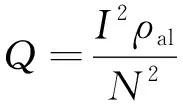
(14)

式中：ρd为材料密度，kg/m3；Cp为恒压热容，J/(kg·K)；k为导热系数，W/(m·k)；q为导热热通量密度，W/m2；Q为热源，W/m3；N为导体的横截面积；I为中心导体流通的直流电流；ρal为电缆芯线的电阻率。

(6)空间电荷输运的迭代求解

与传统的恒温模型和一维几何模型不同，本文考虑了由欧姆热引起的电缆径向存在的温度梯度以及圆形截面的几何特征引起的电场梯度。因此，在计算中引入了傅里叶定律和径向电场梯度，计算结果更贴近于实际电缆的分布特点。

采用有限元对电缆绝缘层中的电荷传输进行仿真，其流程图如图6所示。首先根据电缆实际运行情况设置初始边界条件，在通过求解泊松方程和傅里叶方程得到初始的电场和温度分布，进而根据肖特基定律计算得到阴极和阳极的空间电荷注入量。再求解传导电流方程，得到每个单元层内各类电子和空穴的变化量，进而得到某一时刻的空间电荷分布。判断计算时间是否达到了设定值，若达到则输出电荷和电场分布结果，若未达到设定时间，则增加一个时间梯度继续迭代求解，直到满足时间设定要求。

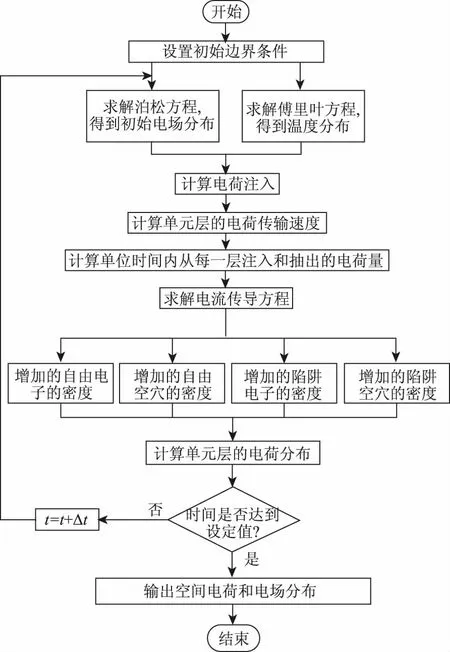
图6 电荷传输模型流程图

迭代的时间间隔Δt应该小于各类载流子入陷、脱陷和复合过程的驰豫响应时间的最小值，同时，需要满足Courant-Friedrichs-Lewy (CFL)条件，具体为，单位时间梯度内空间电荷的输运距离应小于单元域的长度：

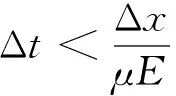
(15)

式中：Δx为模型划分的单元层长度；μ为迁移率；E为电场强度。

2 复合界面对电荷及电场的影响

电缆芯电压U=3 kV、温度为T1=313 K，绝缘屏蔽层外侧接地、温度T2=293 K，径向温度梯度为20 K。单层绝缘(XLPE)电缆与双层绝缘(XLPE/EPDM)电缆附件的空间电荷以及电场分布情况如图7所示。其中，双层绝缘的接口位置在R=140 μm处。

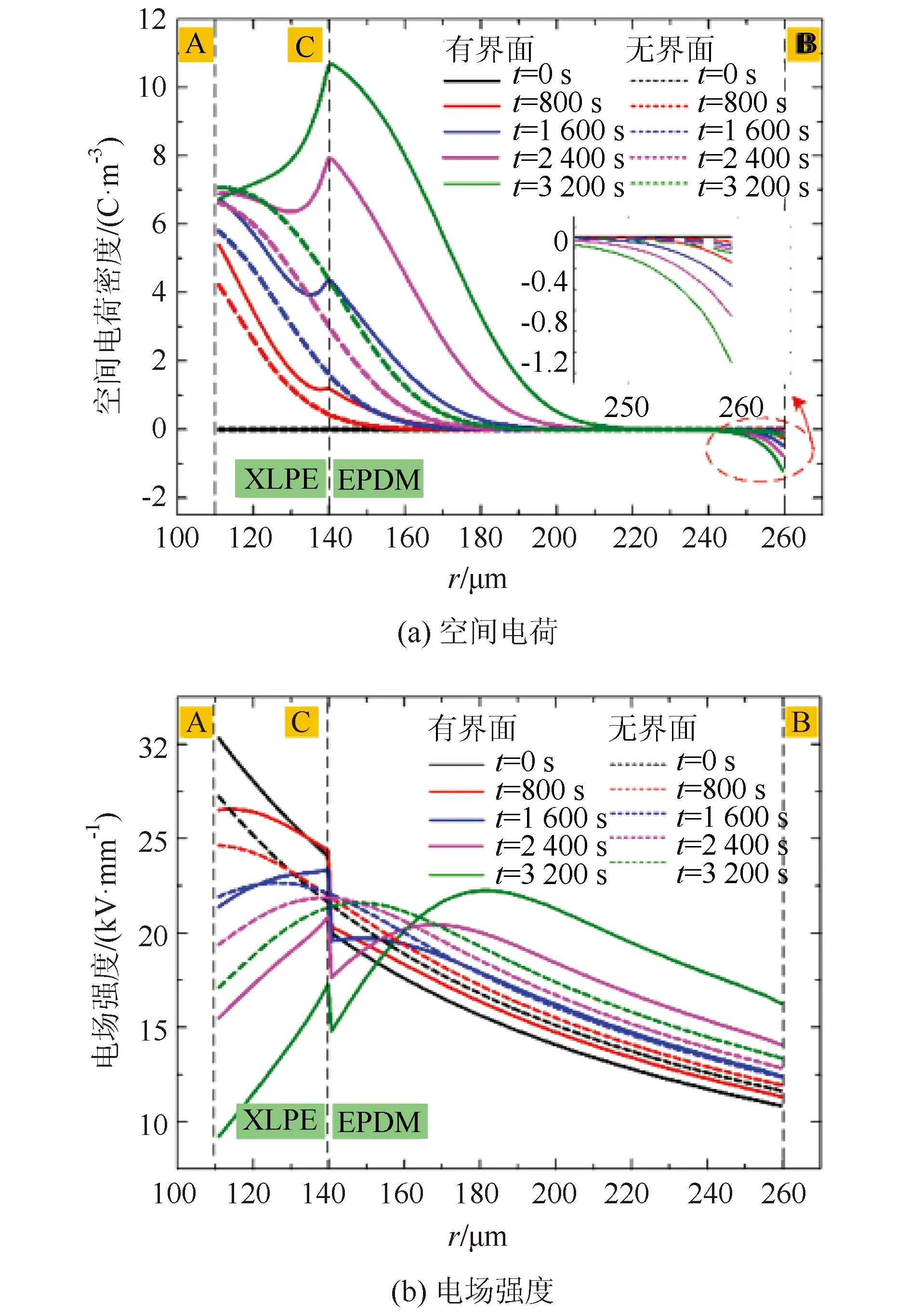
图7 单层电缆和双层电缆在不同时刻空间电荷和电场强度对比图

从图中可以看出，介质材料中电荷密度随时间不断增加；与电子相比，更多的空穴被注入和迁移到绝缘中，其主要原因为缆芯处的电场和温度均高于绝缘屏蔽层处。对于XLPE/EPDM双层绝缘，在界面处积聚大量电荷，当时间足够长时，沿半径方向界面处电荷密度最高。此外，当引入该界面时，其他区域的电荷密度也有增大的趋势。由于界面两侧电荷输运行为的差异和界面的半阻塞效应，电荷在界面处逐渐积累，密度随时间逐渐增大。

如前所述，阳极的高温和电场促进了空穴的注入和迁移。所建立的模型能够再现在电缆中实验观察到的一些具体特征，如最大电场随时间由内侧移动到外电极，以及电场畸变特点。从图7可以看出，本文模拟的电荷和电场的变化规律与前人实验所验证的结果一致。绝缘材料中的传导电流实质上是由各种电荷迁移引起的。因此，双极性电荷输运模型更详细地描述了不同载流子的动态过程。然而利用双极性电荷输运模型研究界面电荷行为的研究较少，该模型从更基本的角度表征了空间电荷积聚的机理。因此，双层绝缘中双极电荷输运特性及优化界面方法有待进一步研究。

3 复合界面最优位置确定方法

3.1 直流电压下电荷和电场分布特点

为指导双层绝缘电缆附件的设计，讨论了界面位置对空间电荷和电场分布的影响。仿真中将电压设为3 kV，温度梯度设为20 K。设置了五个不同的接口位置包括：130 μm、160 μm、190 μm、220 μm和250 μm。由于界面位置的改变，界面电荷密度发生了变化，为了能够更清楚地观察到距离缆芯较远位置的界面电荷，在本部分的仿真研究中适当延长了仿真时间。比较了t=4 800 s时刻不同界面位置下的空间电荷和电场分布，如图8所示。

如图8(a)所示，直流电压下不同界面位置处均有不等量的电荷积累。具体来说，靠近阳极的界面积累了大量的正电荷，而靠近阴极的界面积累了少量的负电荷。这意味着界面电荷的密度和极性与界面的位置密切相关。图8(b)比较了不同界面位置的电场分布。随着界面向阴极移动，界面两侧电场强度的差异先增大后减小，并在该时刻R=190 μm处的界面两侧电场差异最大。在t=4 800 s，不同界面位置的最大电场位于绝缘层中部。在所有界面情况下，R=190 μm时最大电场值最大。

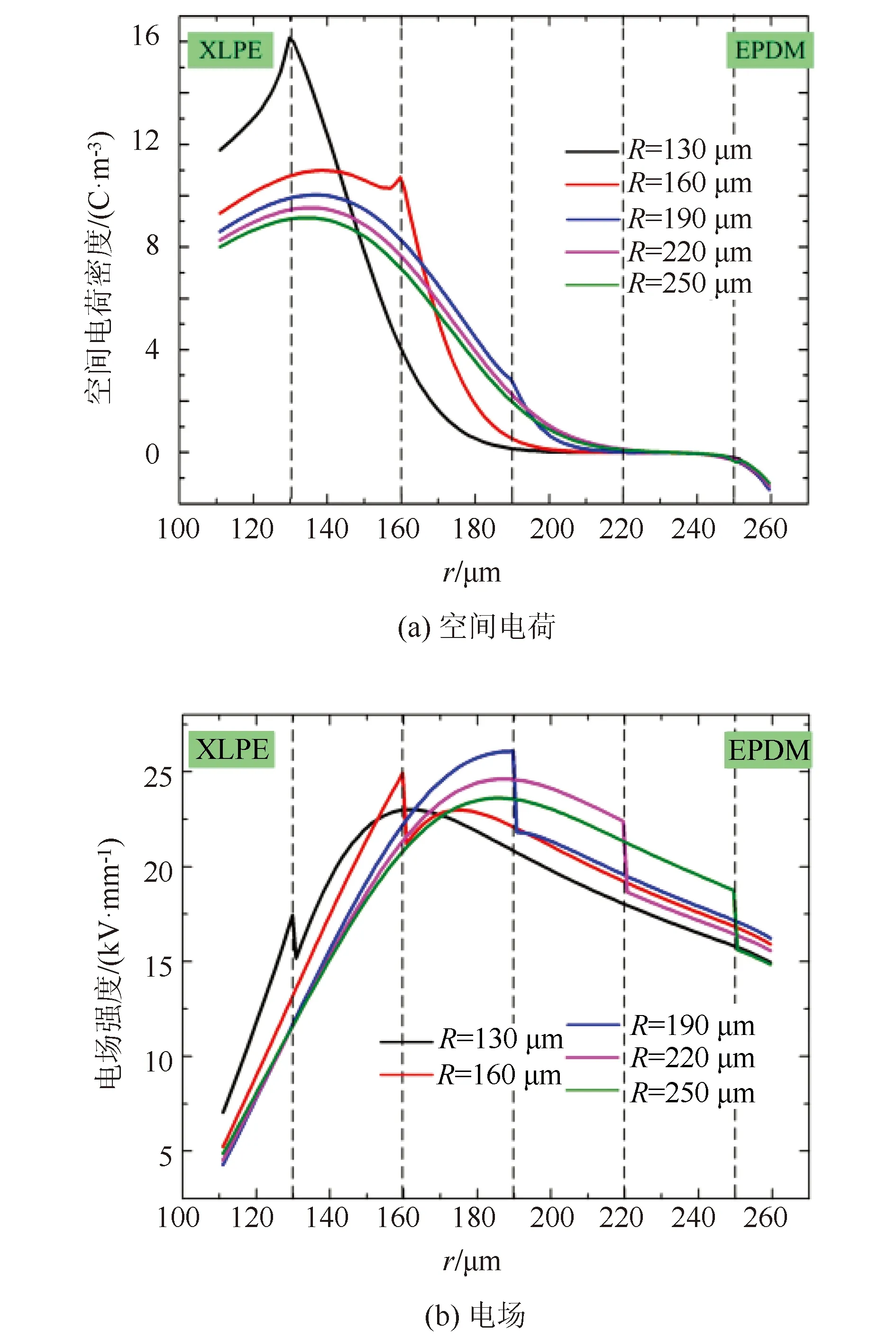
图8 不同界面位置空间电荷和电场分布对比图

图9展示不同界面位置的电缆截面上最大电场强度的瞬态分布结果。为更全面地反映电场的变化，将仿真时间延长到15 000 s。在所有情况下，最大电场均随时间先减小后增大。当界面位于R=190 μm时，电场从t=6 000 s开始明显加强。此外，界面位于R=220 μm和R=250 μm时，最低电场出现在t=1 000～4 000 s时间段内，而最大值45 kV/mm出现在t=15 000 s。这一现象是由电场的翻转引起的，它是由温度梯度、同质电荷和异质电荷的行为导致，即随着时间的推移，最大电场的位置逐渐从阳极向阴极移动。靠近绝缘层外侧的界面增强电场畸变。在整个电缆运行过程中，当界面靠近绝缘层外侧时，电场的不均匀性最强，更容易造成绝缘损伤。

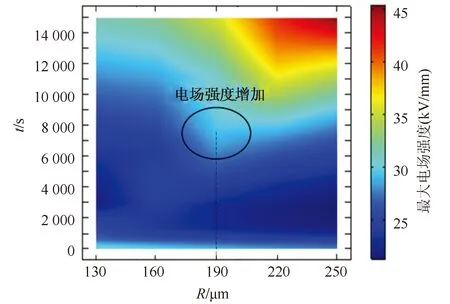
图9 不同界面位置下最大电场随时间的变化情况

为优化双层绝缘的界面位置，本文引入了绝缘利用系数η。绝缘利用系数定义为平均电场与最大电场的比值，它是一个描述电场分布均匀程度的物理量，可表示为

η=Eav/Emax

(16)

式中：Eav为电场强度的平均值；Emax为电场强度的最大值，kV/mm；η无量纲。η越接近1，说明电场分布越均匀。不同界面位置在t=2 000 s，t=8 000 s和t=15 000 s时刻计算得到的绝缘利用系数η值，如图10所示。

图10 绝缘利用系数

由图可知，η随着时间的推移而减少，这表明电场畸变程度逐渐加重。不同时刻η的变化趋势也存在极大的差异。当模拟时间是t=2 000 s时，η随着绝缘界面向阴极移动而略有增加。当模拟时间是t=8 000 s时，η先减小然后增加，当界面位于绝缘层中部时，η到达最小值，即R=190 μm。当时间为t=15 000 s时，η的变化规律与t=2 000 s时完全相反，最小值出现在R=250 μm。

总之，η的最小值出现的位置随着时间的推移逐渐从阳极到阴极移动。特别地，当绝缘界面设置在R≥190 μm时，η在t=15 000 s曲线上迅速减小。数值接近1的η有利于电缆的安全稳定运行，因此，建议复合绝缘界面应避免设置在保温层外侧，且应设置在绝缘层厚度的一半以内的位置，即双层绝缘结构的分层设计应适当增加外绝缘层的厚度。

3.2 极性反转电压下电荷和电场分布特点

极性反转电压是高压直流输电系统中一种常见且必要的运行方式，可以通过电压极性反转来实现电能传输方向的转换。然而，空间电荷的分布并不遵循极性反转规律。极性反转后的外加电场与空间电荷产生的电场叠加，导致电缆运行状态更加严峻。所施加的极性反转电压如图11所示，其中U0=3 kV。

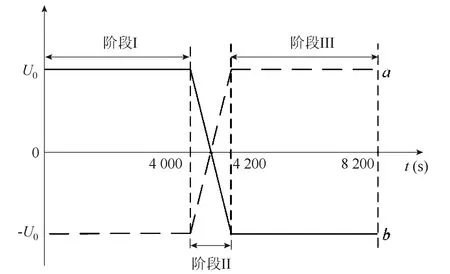
图11 外电压波形

本部分设置的外施电压波形由正变负U0=3 kV和温度梯度Δt=15 K。设置了三个不同的界面位置包括，如图11所示，随着界面向外移动，正电荷密度逐渐减小。在t=4 200 s时，电压反转后的最大电场出现在高温侧。为了进一步分析界面位置的影响，根据图12所示的电场分布结果计算得到不同仿真时间下沿径向的最大电场，如图13所示。

图12 不同界面位置空间电荷与电场强度对比图

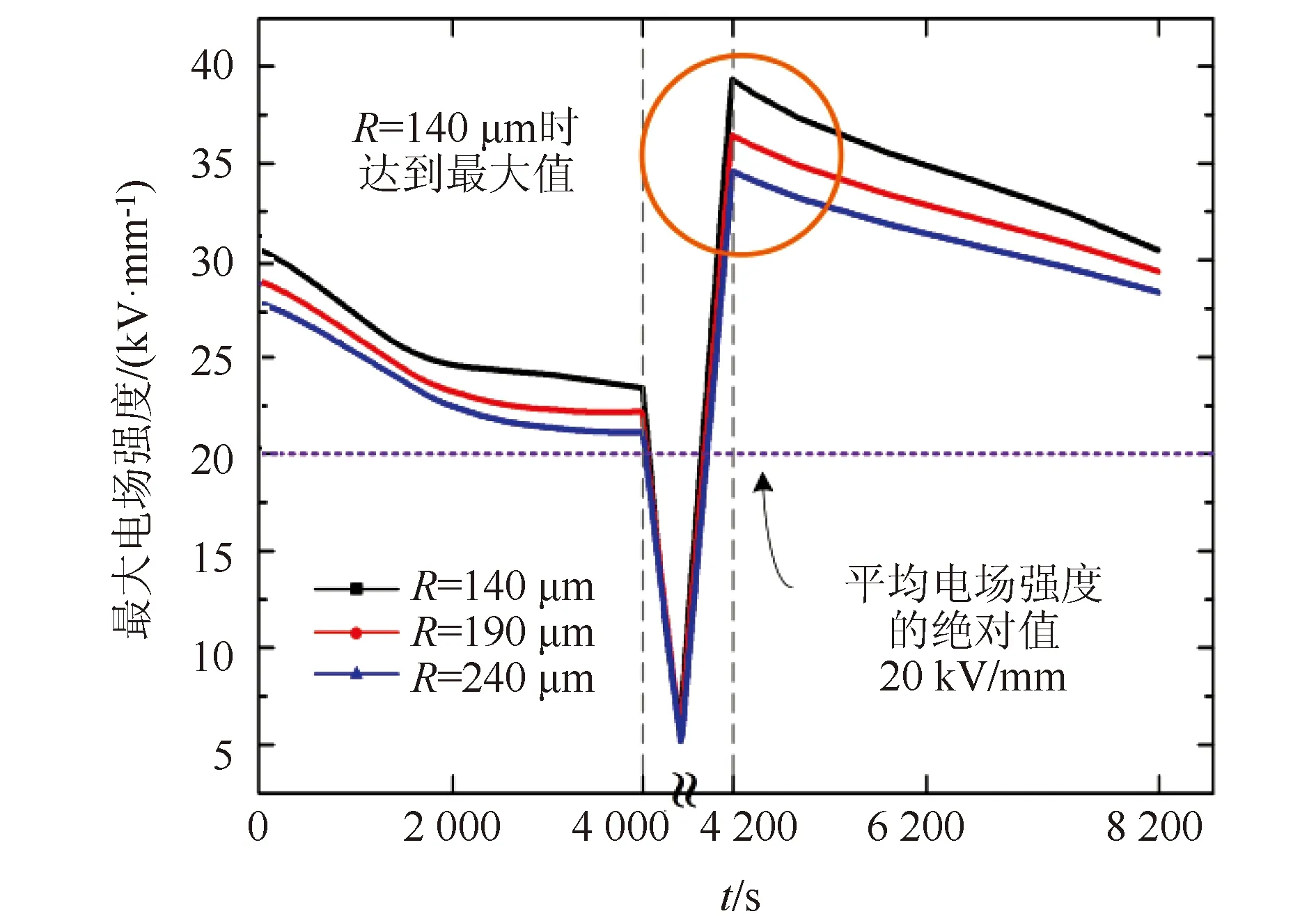
图13 不同界面位置下的最大电场随时间的演化

在t=0～4 000 s时，各点的最大电场均随时间逐渐减小。这是因为在这一时期，最大电场仍然出现在内绝缘层，并且随着电荷的注入而逐渐减小。在阶段III的初始时刻，三种界面条件下的电场均达到最大值，且最大值均出现在绝缘层内侧。其中，当界面位于R=140 μm处时电场的畸变程度最突出。

3.3 复合界面优化设计

为了更加全面地分析直流电压和极性反转电压对电场畸变的影响，设置了5个界面位置，包括R=140 μm，R=165 μm，R=190 μm，R=215 μm和R=240 μm。公式(17)定义了分层半径对应的综合电场畸变因子k。通过以下方式求得：先计算不同电压下的电场畸变因子与加权系数的乘积，然后将求得的数值相加。

(17)

式中：F为分层半径对应的归一化电场畸变因子；ai是外施电压的加权系数；i是不同形式的外部电压，包括直流电压和极性反转电压；n表示外施电压的数量；j=1，2，…，5，分别相应的界面位置为R=140 μm，R=165 μm，R=190 μm，R=215 μm和R=240 μm。

本文将直流电压和极性反转电压的加权系数都设定为0.5。如果有其他形式的电压，可以推广公式，根据需要调整加权系数的设定值。计算电缆在直流电压下运行15 000 s时刻和极性反转电压第III阶段初始时刻的电场畸变因子，如表2所示。

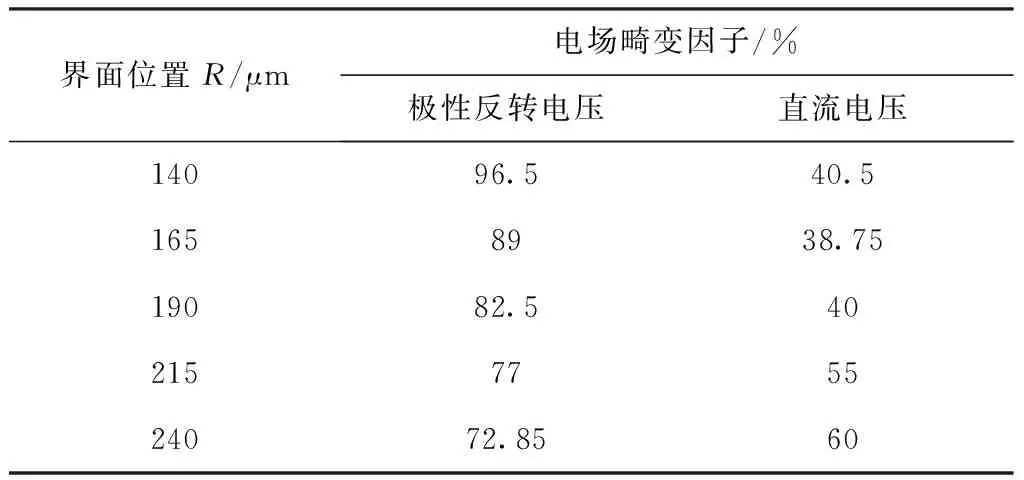
表2 电场畸因子与界面位置的关系

从表2中可以看出，界面靠近绝缘层内侧R=140 μm时极性反转电压下电场的畸变值最大，当界面靠近绝缘层外侧R=240 μm时，直流稳态运行时的电场畸变值最大。将两组数据进一步进行归一化处理，根据式(17)计算出综合电场畸变系数k，如表3所示。综合电场畸变因子k与界面位置的关系如图14所示。

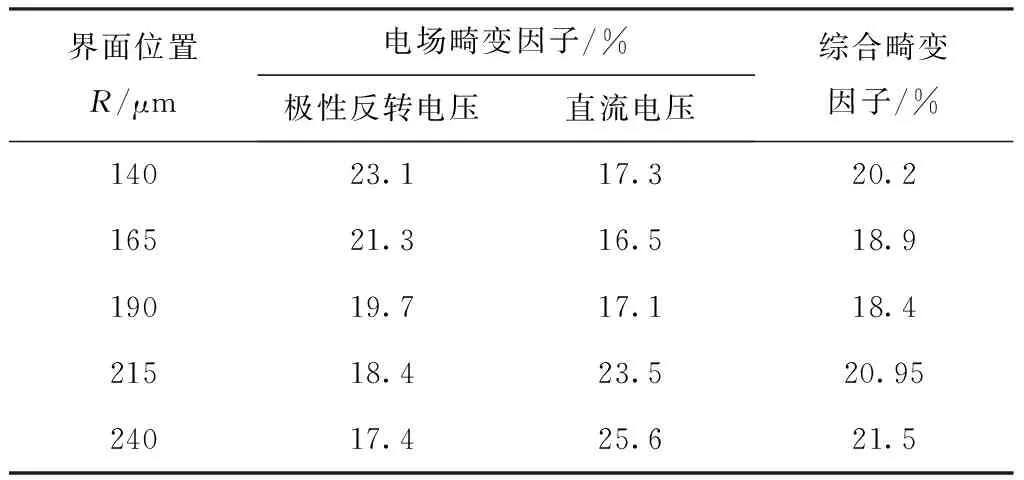
表3 不同界面位置的综合电场畸变系数k

从图14中可以看出，随着界面从阳极向阴极移动，k值先减小后增大。当界面位于绝缘层中间时，k值最小。因此，在电缆分层设计中，将接口置于绝缘层的中间部分，有利于电缆的安全稳定运行。

图14 电场畸变因子与绝缘界面位置的关系

4 结 语

本文采用建立双极电荷输运的一维轴对称模型，模拟双层绝缘电缆在直流电压和极性反转电压下的空间电荷分布，研究了界面位置对空间电荷和电场分布的影响规律。得到结论如下：

1)直流电压下，界面电荷的密度和极性与界面的位置密切相关。当界面靠近阳极时，界面电荷呈现正极性状态；当界面靠近阴极时，界面电荷呈负极性。此外，当界面靠近绝缘外侧时，绝缘利用系数最低，更容易引起绝缘击穿。

2)在极性反转电压下，最大电场出现在电压完全反转的初始时刻。极性反转前的剩余电荷使电场显著增强，而最大的瞬态电场出现在高压电极上，即当界面位于绝缘层内侧时，极性反转电压下的电场畸变最为严重。

3)本文提出计算最优界面位置的方法，引入综合电场畸变因子，计算结果表明在工程实际的电缆附件分层设计中，绝缘层中间的界面有利于电缆的安全稳定运行。