基于LSTM-Attention的毫米波雷达行人轨迹预测方法
翟靖宇, 陈金立
(南京信息工程大学, 江苏 南京 210044)
0 引 言
随着智能交通系统的迅速发展,行人轨迹预测已经成为一个重要的研究方向并应用于诸多场景,如:无人驾驶技术中的行人定位与规避[1];道路安全监控中的行人跟踪[2]等。提升行人轨迹预测的精度对于提升交通安全具有重要意义。
行人轨迹预测指根据行人的历史轨迹,预测其未来可能出现的位置。文献[3-5]通过计算机视觉获取行人的地理位置,该方法可以获得较好的定位效果,但非常依赖摄像头采集的图像的质量,易受光照、烟雾等环境因素的影响,同时存在个人隐私泄露的问题。相比于光学相机,毫米波雷达具有全天候的工作能力,它通过天线发射电磁波,然后处理并分析接收的回波信号,进行目标检测与定位,具有距离分辨率高、发射功率低、穿透能力强[6-7]的特点。应用毫米波雷达对行人跟踪定位已经得到初步应用,并成为一个重要的研究热点方向[8]。
目前,行人轨迹预测的方法主要有两类:基于运动学模型的预测方法和基于深度学习的预测方法。常用的行人运动学模型主要有恒速度(Constant Velocity,CV)模型、恒加速度(Constant Acceleration,CA)模型等。卡尔曼滤波(Kalman Filter,KF)算法在预测频繁变化的系统状态方面具有优势,能够对系统的运行状态进行最优估计,实现对运行状态的实时预测[9]。文献[10]结合恒速度模型和卡尔曼滤波算法预测行人轨迹。但卡尔曼滤波算法需要事先建立系统的运动状态方程,而行人的运动状态复杂多变,具有较高的非线性,难以用单一的运动状态方程准确概括。深度学习以神经网络为主要模型,通过大量数据样本的训练更新网络参数,能够拟合具有较高非线性的系统,完成较为复杂的任务。通过深度学习方法训练的模型预测精度高,鲁棒性强。循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络,能够自适应学习网络参数,在预测动态变化的行人轨迹方面具有优势[11]。但由于存在“梯度消失”和“梯度爆炸”问题,循环神经网络无法对长时序列进行有效建模,LSTM网络是RNN的一种变体,由于引入了门口机制来控制信息的累计速度,能够改善循环神经网络的长程依赖问题,在具有时序特征的数据预测场景中得到广泛应用[12]。文献[13]构建多个LSTM模型预测不同场景中的行人轨迹;文献[14]从视频监控中提取行人的骨架及头部方向特征,作为意图预测网络的输入,继而得到行人意图,将行人意图预测类别和历史轨迹坐标的联合向量作为LSTM网络的输入,提高行人轨迹预测的准确性。在模型学习过程中引入Attention机制,可以加强网络对各个时刻编码向量的有效利用,进一步提高模型的预测性能[15]。
因此,本文采用毫米波雷达实时探测行人,建立行人轨迹数据集。针对传统的运动学模型和单一LSTM模型无法准确描述行人复杂的运动状态、预测精度低以及鲁棒性差的问题,本文提出一种基于LSTM-Attention神经网络的行人轨迹预测模型,利用LSTM网络提取行人轨迹序列特征,并引入注意力机制,强化模型对轨迹特征的关键信息的抽取能力,进一步提高了模型的预测精度。实验结果表明,本文提出的LSTM-Attention行人轨迹预测模型相较于传统的运动学模型和单一的LSTM模型,能够预测各种复杂度的行人轨迹,预测精度更高,鲁棒性更强。
1 行人位置数据的获取
如图1所示,本文建立人体回波信号模型,对中频信号做距离维FFT频谱分析得到行人的距离,利用相位法测角获取行人的方位角。对测得的行人距离和方位角进行极坐标转直角坐标变换得到行人位置。

图1 行人位置数据获取原理图
1.1 行人回波信号模型
如图2所示,毫米波雷达使用线性调频信号作为发射信号,一个调频周期内的发射信号为
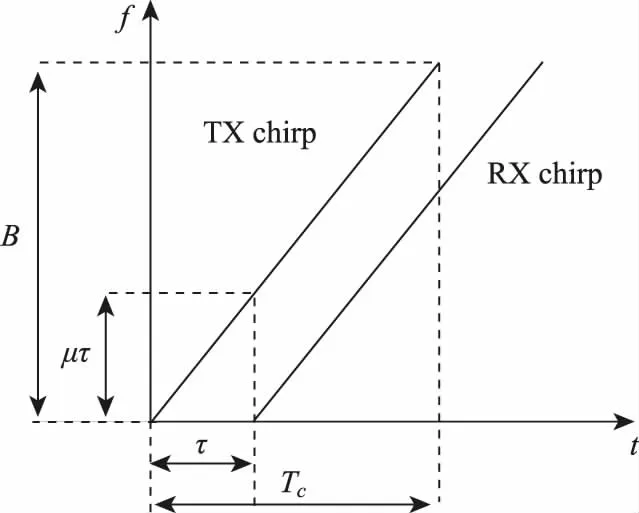
图2 线性调频原理图
(1)
其中,
μ=B/Tc
式中:AT为发射信号的的幅度;fc为雷达载频;μ为调频斜率;B为带宽;Tc为信号的调频周期。发射信号经过行人反射后,接收天线收到回波信号为
(2)
其中,
τ=2R/c
式中:AR为回波信号的幅值;τ为回波信号的瞬时时延;R为雷达与所测行人的距离;c为光速。回波信号经过混频、滤波处理后可以得到中频信号
Q(t)=S(t)R*(t)=Aqexp[j(2πfqt+φ)]
(3)
其中,
Aq=ATAR
fq=μτ
式中:Aq为中频信号的幅值;fq为中频信号的频率;φ为中频信号的初始相位。对中频信号Q(t)的采样点数据做距离维FFT可以得到中频信号频率fq。行人的距离可表示为
(4)
1.2 相位法测角
对于同一行人,可以通过两个接收天线接收的回波信号的相位差估算其方位角θ[16]。如图3所示,假设相邻两个接收天线的距离为d,行人与接收天线间的距离R≫d,则两条接收射线近似平行。两个相邻接收天线接收回波的路程差可近似为
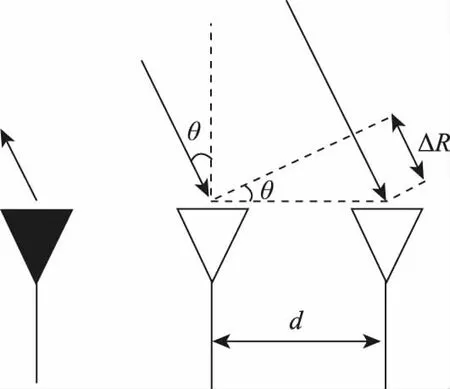
图3 相位法测角原理图
ΔR=dsinθ
(5)
两个接收回波的相位差Δφ和路程差ΔR存在如下关系
(6)
式中:λc为回波信号的波长。由式(5)和式(6)可知,行人的方位角可表示为
(7)
通过坐标变换,可得到行人位置的二维坐标如下
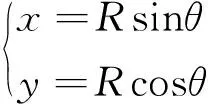
(8)
由此可构建行人轨迹数据集
P:{(xi,yi),i=1,2,…,I}
(9)
2 LSTM-Attention行人轨迹预测模型
2.1 任务定义
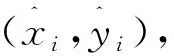
(xi-1,yi-1)])
(10)
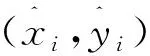
2.2 模型整体结构
如图4所示,整个LSTM-Attention行人轨迹预测模型包含4部分。
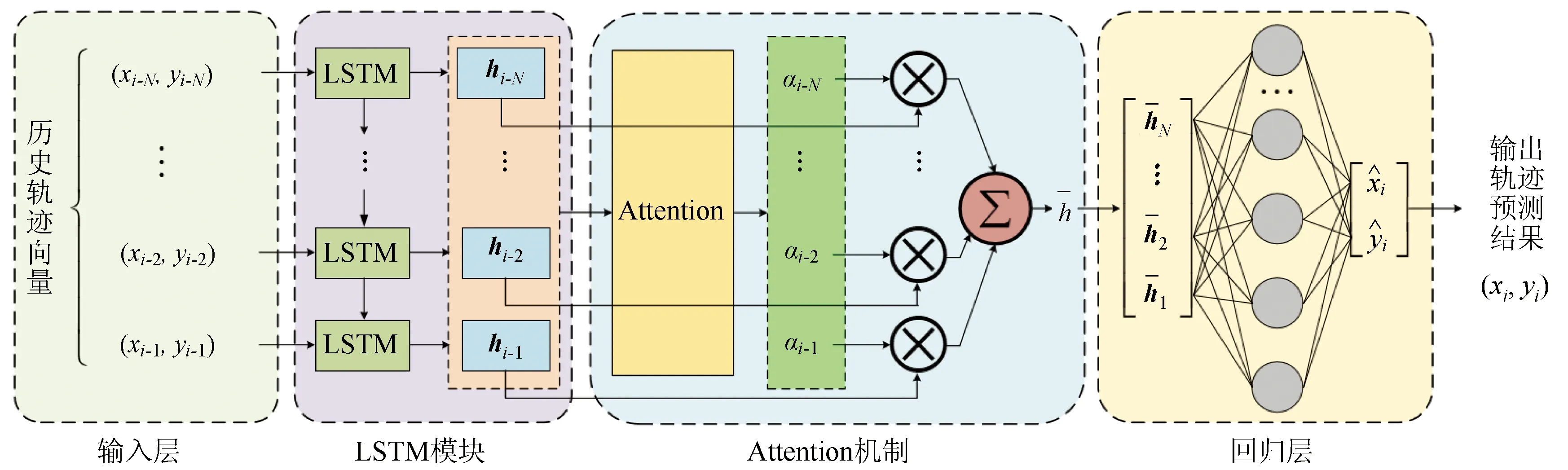
图4 行人轨迹预测模型结构图
1)输入层。该部分对毫米波雷达采集的行人轨迹数据集P进行分段处理,每N个连续的轨迹向量为一组作为输入序列依次输入到模型中。
2)LSTM模块。该部分负责提取行人轨迹数据前后的关联性,在k(1≤k≤N)时刻输出与当前输入的轨迹向量(xi-k,yi-k)相对应的编码扩充后的输出向量hi-k,hi-k中包含了输入轨迹的特征信息。
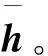
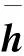
2.3 LSTM网络
LSTM网络是RNN的一种变体,能够提取序列数据前后的关联性。其通过引入门控机制,有选择地引入新的输入信息,并有选择地遗忘过去累积的信息,缓解了RNN随着递归次数的增加,出现权重指数级爆炸或消失现象,网络收敛困难的问题,在序列数据处理的场景中得到广泛应用[17]。
LSTM网络由多个LSTM记忆单元按时间次序连接而成的[18]。LSTM记忆单元的结构如图5所示,假设当前时刻为i,则过去第k时刻的外部输入的轨迹向量为(xi-k,yi-k),输出向量为hi-k,⊙表示向量的点积运算,σ(·)为Logistic函数。记忆单元内部通过遗忘门Fi-k、输入门Ii-k以及输出门Oi-k三种运算机制协同控制信息的更新、累积与遗忘,具体操作流程如下:
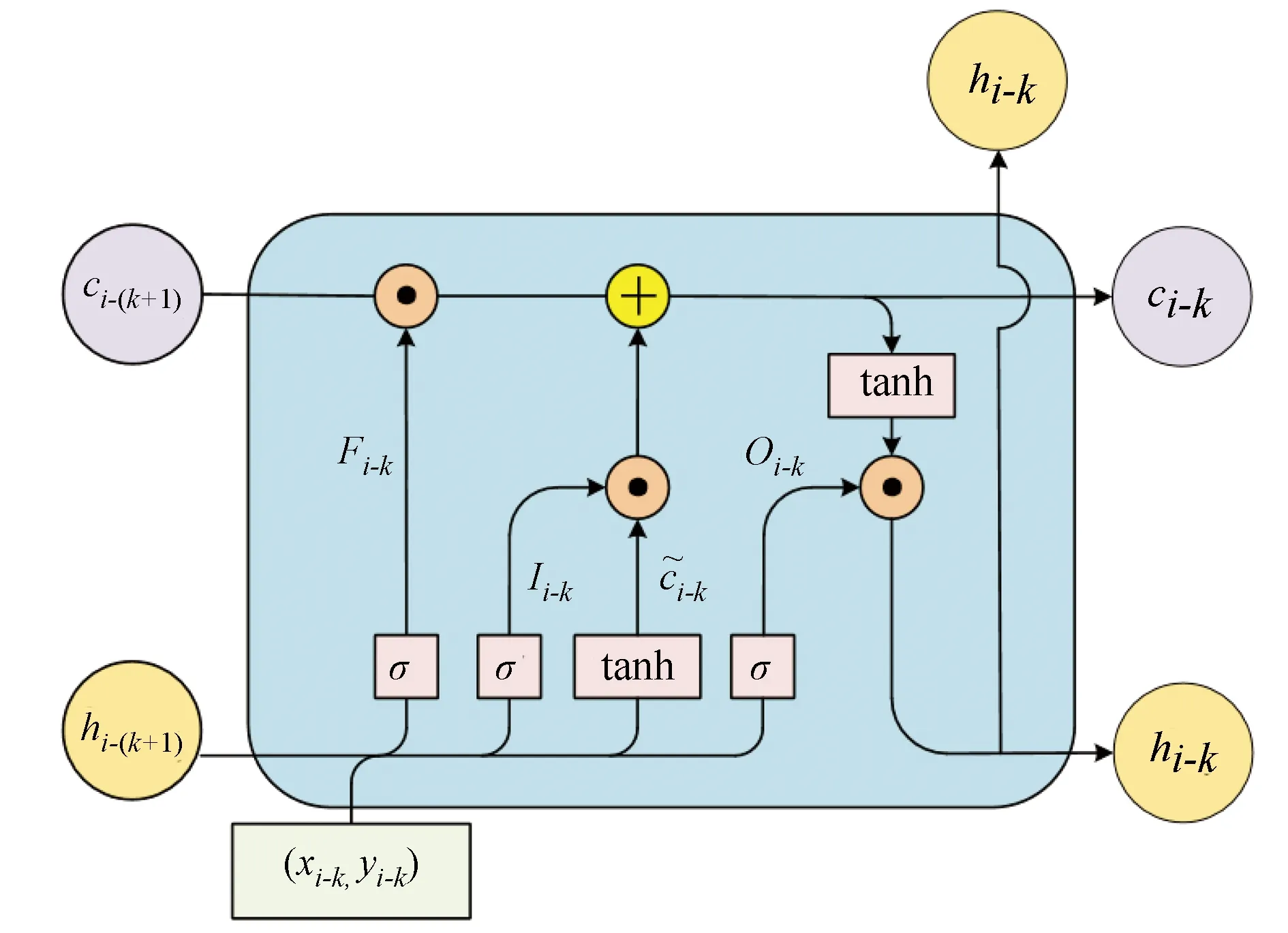
图5 LSTM记忆单元结构图
1)信息的选择遗忘。式(2)中ci-k为网络的内部状态,表示网络学习到的轨迹信息。通过遗忘门Fi-k(Fi-k向量内部元素的取值介于0~1)对上一时刻网络学习到的轨迹信息ci-(k+1)选择性过滤。
Fi-k=σ(WF·[hi-(k+1),(xi-k,yi-k)]T+bF)
(11)
式中:WF,bF为网络参数。
(12)
式中:Wc,WI,bc,bI为网络参数。
3)信息的选择输出。式(13)中使用激活函数tanh(·)对当前时刻内部状态信息ci-k进行压缩处理,通过输出门Oi-k控制网络内部信息反馈到网络外部的情况,得到当前时刻网络的输出向量hi-k。
(13)
式中:WO,bO为网络参数。
2.4 Attention机制
在行人轨迹预测模型中引入Attention机制,如图6所示,可以使模型自适应地聚焦于对任务影响最显著的输入特征,提高模型的运算效率和预测精度。具体计算过程如下:
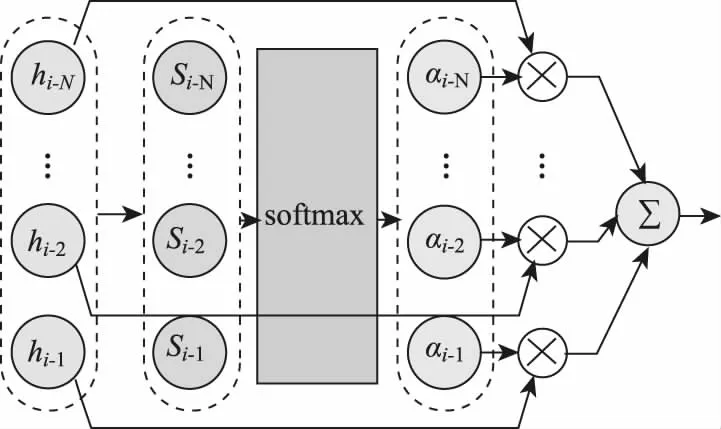
图6 Attention机制结构图
(14)
式中:Ws,bs,vs为网络参数。
3 实验验证
本文使用TI公司的IWR6843毫米波雷达采集操场上行人的轨迹数据来对本文的LSTM-Attention轨迹预测模型进行训练和测试。毫米波雷达带宽为4 GHz,单位帧下的Chirp数为128,帧周期为40 ms。在行人轨迹数据采集过程中,用三脚架将毫米波雷达固定在约1.5 m的高处,如图7所示。选定行人轨迹的采集范围:xl=-25 m,xr=25 m,yl=1 m,yr=50 m。PC端每隔1 s采集一次行人的位置。采集100组行人轨迹,每组轨迹包含100个行人位置数据。为使数据具有更好的泛化性,选取性别、身高、年龄各不相同的12名行人来进行轨迹数据采集,建立行人轨迹数据集。为验证本文提出的轨迹预测模型的有效性,选取了结合KF算法的CV模型以及传统LSTM模型作对比分析,实验流程如图8所示。

图7 实测场景图
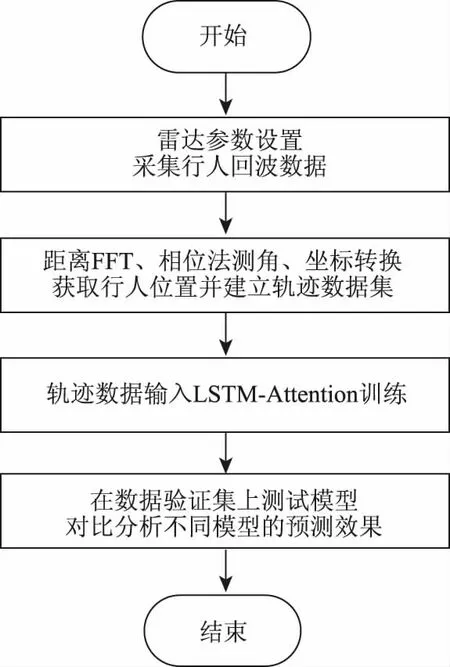
图8 实验流程
3.1 模型参数与训练过程
模型的输入序列长度N为8,输入向量维度为2,LSTM隐藏层数为1,节点数300,学习率为0.000 4,激活函数为Relu函数。采用批量训练的方式,每批包含72段轨迹序列。网络训练采用RMSprop优化算法[19],采用均方误差(MSELoss)作为训练的损失函数,网络迭代训练次数设置为300次。
模型在训练过程中的误差变化趋势如图9所示,LSTM-Attention轨迹预测模型误差不断下降,测试集误差和训练集误差收敛到一起,最终误差降为0.035,说明模型训练效果良好。
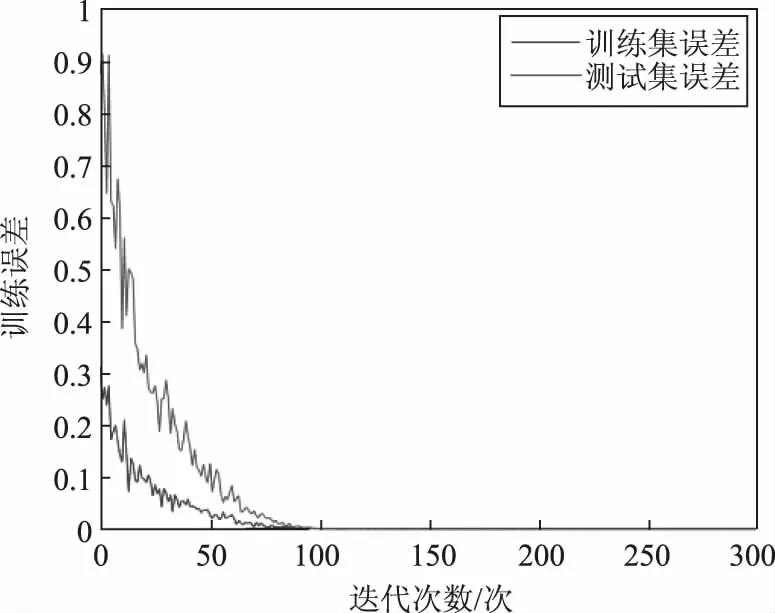
图9 模型误差曲线
3.2 评价指标
采用平均位移误差[20](Average Displacement Error,ADE)作为轨迹预测模型的评价函数,表示真实轨迹与预测轨迹的L2欧氏距离。
(15)
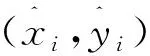
3.3 实验结果与分析
3.3.1 验证集预测性能对比
行人轨迹验证集在CV-KF、传统LSTM和本文的LSTM-Attention上的预测误差对比见表1,表中描述了三种模型的轨迹横坐标、轨迹纵坐标以及轨迹位移的平均误差和最大最小误差。上述指标的数值越小表示模型预测与真实偏移越小,模型预测精度更高。表1结果表明,本文提出的LSTM-Attention模型相较于结合卡尔曼滤波的运动学模型和传统LSTM模型,行人轨迹预测性能更优。
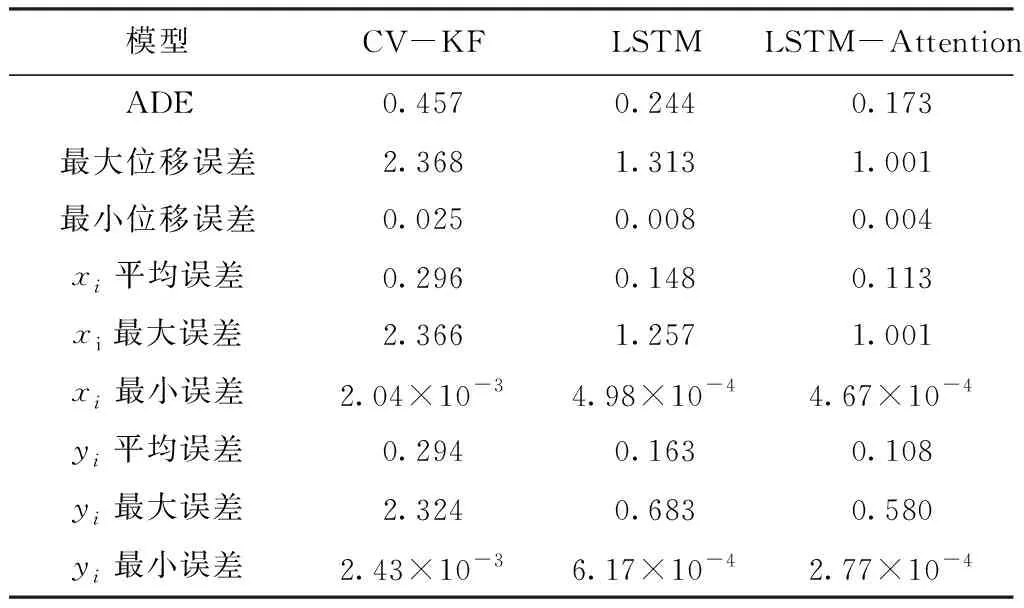
表1 验证集数据对比表 m
3.3.2 不同复杂度轨迹预测性能对比
为定量分析不同轨迹段的预测性能,本文定义轨迹复杂度(Trajectory Complexity,TC)对行人轨迹数据集进行划分。
(16)
其中,
式中:N为一段轨迹的轨迹点数;Pk表示行人位置坐标;dk表示相邻两个轨迹点的位移向量;|Δdk|表示相邻位移向量变化的大小。如图10所示,|Δdk|变化越频繁,则行人位移的大小和方向改变越频繁,轨迹越复杂。

图10 行人轨迹示意图
由图11可知,随着轨迹复杂度的提高,行人的运动状态难以用理想的运动学模型概括,CV-KF模型的预测误差呈上升趋势。传统的LSTM模型能够提取不同轨迹向量前后的关联性,较好地预测不同复杂度的轨迹,鲁棒性强。本文提出的LSTM-Attention在传统LSTM模型的基础上引入注意力机制,使模型能够自适应地聚焦于对当前轨迹预测影响最显著的轨迹特征,进一步提高了模型的预测精度,在各种复杂度的轨迹预测中,预测精度均高于另外两种模型。
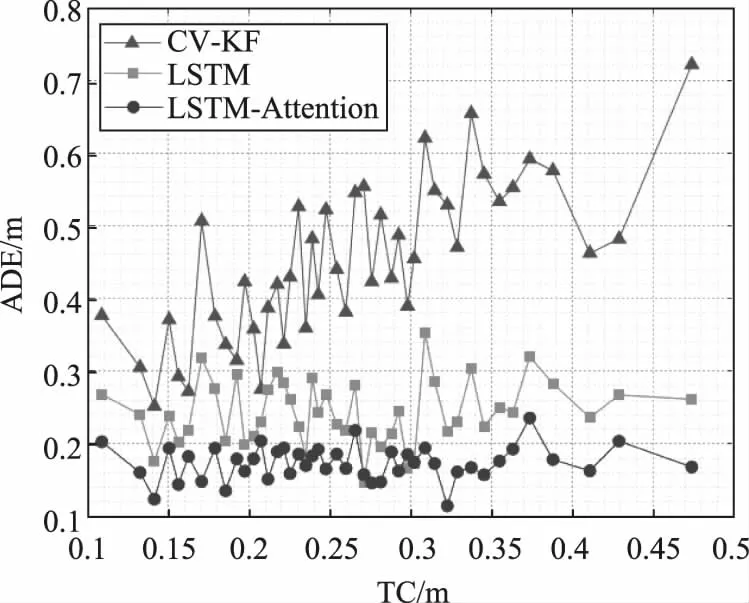
图11 不同复杂度轨迹预测性能对比图
图12给出轨迹复杂度分别为0.24 m、0.34 m、0.37 m、0.47 m的预测轨迹可视化对比图,由图可知,相较于其他轨迹预测模型,本文提出的LSTM-Attention模型的预测轨迹更贴合真实轨迹。
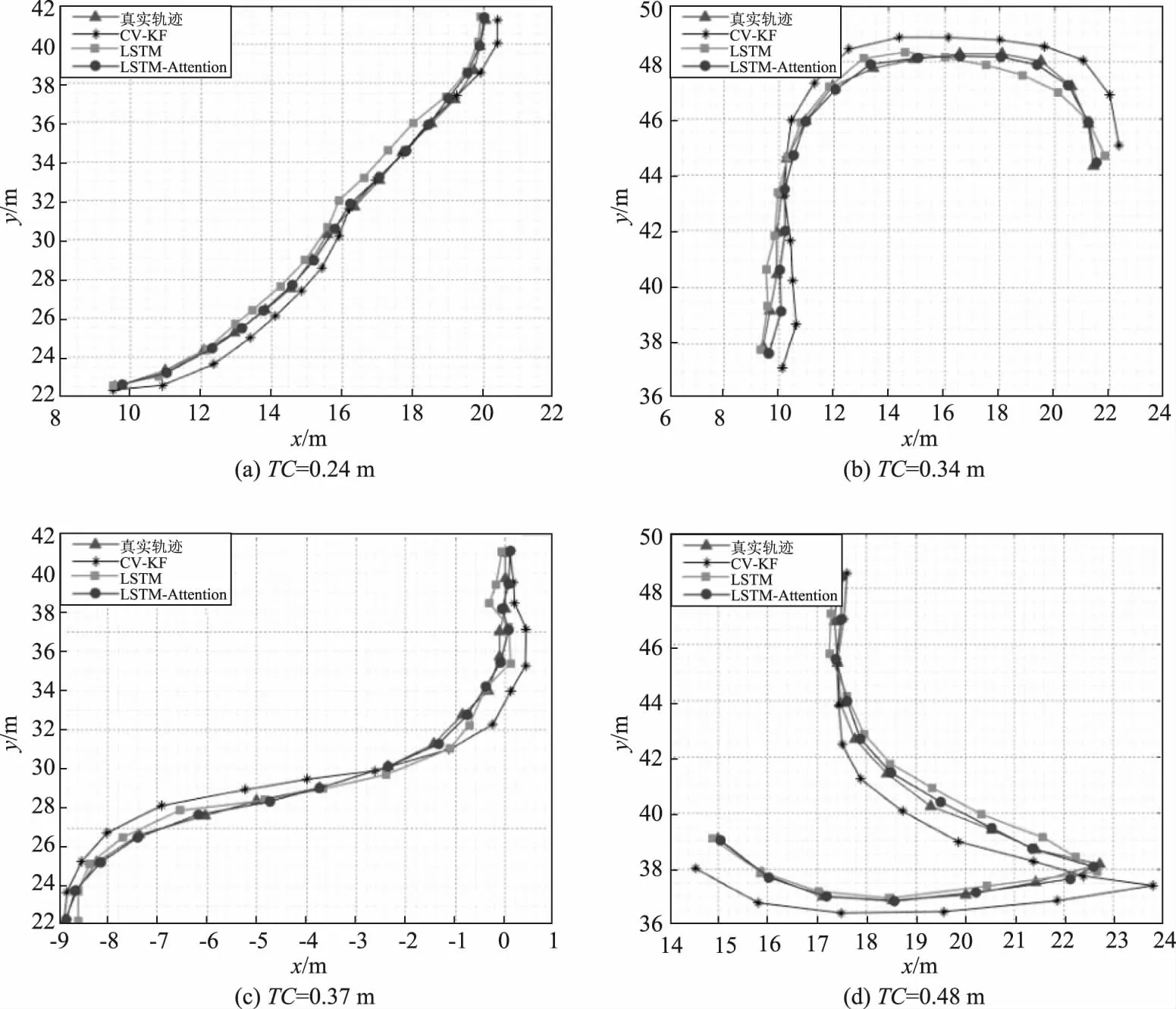
图12 预测轨迹可视化对比
4 结 语
本文提出一种基于LSTM-Attention的毫米波雷达行人轨迹预测方法,能够在保护行人隐私的前提下和光线较弱的环境中工作。利用毫米波雷达建立了行人轨迹数据集,设计了LSTM-Attention行人轨迹预测模型。针对行人轨迹数据的强时序性,采用LSTM网络提取轨迹特征,并引入Attention机制,自动抽取轨迹特征中的关键信息。实验结果表明,本文提出的LSTM-Attention轨迹预测模型在预测精度性能方面优于CV-KF模型、传统LSTM模型,并且能够较好地预测各种复杂度的轨迹,模型的鲁棒性更好。后续研究会考虑行人与环境的交互情况,和轨迹序列组成联合向量,丰富模型的输入特征,进一步提高模型的预测精度和实用性。

