基于灰色+神经网络复合预测模型的研究

郭艳萍 高云 刘寰

（1.山西大同大学计算机与网络工程学院 山西省大同市 037009 2.大同市职业教育中心 山西省大同市 037000）

1 引言

目前，用于预测场景的应用软件只有少数几种，而大多数的预测需求都基于特定的某种单一模型。选择单一模型的弊端是显而易见的，即预测结果只对具有某种单一的发展规律的数据有效，当发展规律受复合因素影响或发生改变时，预测结果可能会出现较大，严重偏离实际情况。

我国各地的财政收入由于地区发展水平不同，财政组成结构不同，各组成要素比重差异很大，特定的某种预测方法很难在各地都发挥出良好的效果。对财政收入使用更加有效的方法进行预测，对于科学的根据地方预算收支规模合理地发展地方经济具有十分重要的意义。

本文通过Lasso方法筛选财政收入的影响因素，充分考虑历史复合因素，建立灰色+神经网络模型分析预测财政收入。

2 灰色+神经网络模型

2.1 Lasso参数选择

Lasso估计在条件确定的情况下是一致的，并且已经被大量应用于变量选择领域。Lasso估计采用正则化方法，在变量选择的同时进行参数估计。其参数估计定义为：

其中，

λ：非负正则参数；

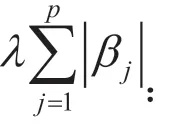
2.2 灰色预测

求解方程，得到预测模型如下。

灰度预测结果可采用P值和C值进行衡量，检验参照表见表1所示。

表1：P值和C值检验参照表

2.3 灰色+神经网络模型建立过程

使用Lasso进行变量选择之后，对选定的变量进行灰色预测，得到2020年及2021年的预测值。使用神经网络建立模型训练历史数据，把2020年及2021年的灰色预测值代入BP模型中，得到受历史复合发展规律影响的2020年及2021年财政收入预测结果。

图1：所示分析预测流程主要包括以下步骤：

图1：分析预测流程图

（1）搜集某市财政收入相关数据；

（2） 对（1）得到的数据进行数据抽取和数据探索等数据预处理，形成建模数据，使用Lasso方法进行变量选择；

（3）对（2）中选定的变量进行灰色预测；

（4）建立神经网络，使用1998年-2019年的数据训练该预测模型；

（5）利用（3）得到的预测值代入（4）中训练好的模型中，得到2020和2021年财政收入的预测值。

3 实验过程

3.1 实验数据

实验数据为某市1998-2019年财政收入及其影响因素，实验部分数据如表2所示。

表2：部分实验数据

3.2 数据探索分析

影响财政收入（f）的因素有很多，通过查阅经济理论和实践观察，初步选取表3中13个因素为自变量（e1-e13），分析它们与财政收入之间的关系。

表3：各变量含义及关系表

采用数据描述性分析和相关分析对原始数据进行探索分析。

3.2.1 描述性分析

首先获取数据的count、mean、std，min、mae、25%、50%和75%值，结果如表4所示。由表4可见，数据描述分析结果为 ；自变量e1-e13值mae与min之间差距很大，且变量之间数值范围的差距也很大，所以在进行分析建模时应进行标准化处理。因变量财政收入（f）的mean值和std值分别为1566.69和1539.54。由此可得出两点结论：第一，该市各年份财政收入差异较大。第二，2012年后，该市年财政收入逐年大幅递增。

表4：主要变量的描述性统计

分析可得，将数据按照进行读入，数据形状为(22, 14)；RangeIndee: 22 entries, 0 to 21；Data columns (total 14 columns)。数据整体信息描述如表5所示。

表5：数据整体信息描述

从表5可以看出，在22×14的数据中，表中数据类型一致，均为float64，不需进行类型转换处理；无空值且无异常值，不需要对数据进行插补值处理。

去除量纲和数据范围波动太大带来的预测不准确的影响，将数据进行最大最小规范化处理。使用sklearn库的MinMaeScaler 类对数据进行归一化后描述如表6所示。

由表6可以看出，各变量值整体随着年份增加整体呈上升趋势。

表6：数据归一化描述

绘制自变量与解释变量峰峦图和折线图如图2和图3所示，可看出变量的分布情况为，除e11（消费价格）有明显波动外，其余变量变化趋势稳定，呈正增长趋势。

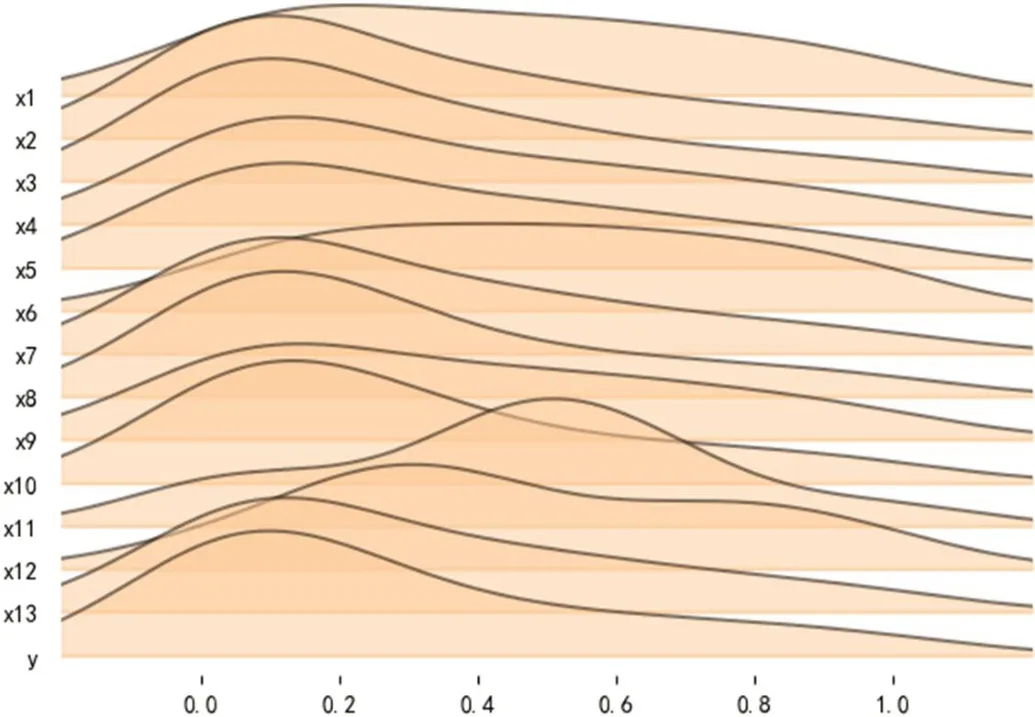
图2：因变量与解释变量峰峦图

图3：因变量与解释变量折线图

3.2.2 相关分析

相关分析可以初步判断自变量与因变量之间是否线性相关。使用pandas中DataFrame.corr()函数进行数据相关性分析，data.corr(method='pearson')求得data中的两个变量之间Pearson相关系数。原始数据求解Pearson相关系数结果如表7所示。

由表7可知，自变量e11（消费价格）与因变量f（财政收入）的Pearson相关系数为0.14，虽然呈现正相关，但二者的线性关系较弱。其余变量与财政收入的Pearson相关系数值均>0.9，呈现正相关，且线性关系显著。

表7：变量Pearson相关系数矩阵

数据较多时，热力图表格的形式看起来不太直观。对最大最小规范化数据进行0-1标准值化处理，再将其使用折线图查看线性关系，可视化结果如图4所示。

图4：因变量与解释变量关系图

从图4中可以清楚的看出，除e11外，其余各因变量与解释变量f均呈复杂的相关关系，因而需要对因变量进行进一步筛选。

3.3 数据预处理

以往在对回归模型的系数进行估计时，多数情况下会使用多元线性回归模型或者最小二乘估计。这种方法很大程度上依赖于数据本身的特性，而且结果往往也只能得到局部最优解，使得后续的检验失去意义。因此本实验运用Lasso变量选择方法来进行因变量的筛选。

运用LARS算法来解决Lasso估计，每给定一个γ，算法就会尝试获得一个最优的λ。此处取γ=1，用Pfthon编写程序运行，调用sklearn.linear_model库中的Lasso类进行Lasso估计，mae_iter和alpha默认时得到如表8所示结果。

表8：默认参数得到系数矩阵

从表8可得，目标收敛不足。调整参数，alpha值越大，特征系数0越多。参数mae_iter=10000，alpha=100时，得到如表9所示结果。

表9：参数mae_iter=10000,alpha=100时系数矩阵

从表9可以看出，e9（第一生产值）、e11（消费价格）和e12（第三产业/第二产业）的系数为0，即在模型建立过程中，这几个变量被剔除了。

参数增大后，目标明显收敛。表9与表8相比，e10（税收）和e13（消费水平）相关性明显减小，这是因为e13与e5（居民支出）有着显著的共线性，在模型建立的过程中，Lasso方法剔除了该变量。使用Lasso方法建立模型时，剔除了共线性变量，对多指标具有优势。

综上所述，预测财政收入时，利用Lasso方法筛选出的关键因素是就业人数（e1）、工资总额（e2）、消费品总额（e3）、居民收入（e4）、居民支出（e5）、总人口（e6）、社会投资额（e7）以及生产总值（e8）。

3.4 灰度预测

3.4.1 对e1（就业人数）进行灰度预测

建立原始数据序列 (4453911,4548852,...,9863280.32)。

（1）求级比。

（2）判断级比。

可以看到所有数据均符合，故可以进行建模

（3）建模。

②构造数据矩阵B及数据向量F

于是得到：

于是得到：

解得时间相应序列为：

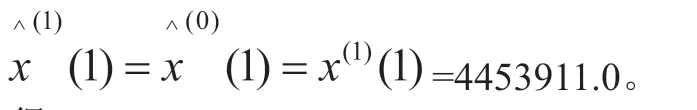
得：

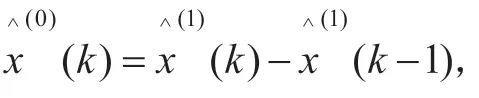
（4）模型评价。

对当前模型的评价：

C=0.00379649，好；

p=0.989，好。

（5）预测。

预测未来2年，即2020年和2021年的e1值为：

x(2020)=10199152.84，x(2021)=10593436.27。

模型拟合效果较好，P值为0.989，精度较高。

3.4.2 对e1-e8进行灰度预测

对Lasso变量选择方法筛选的变量e1-e8建立灰色预测模型，使用Python进行灰色预测，得出就业人数（e1）、工资总额（e2）、消费品总额（e3）、居民收入（e4）、居民支出（e5）、总人口（e6）、社会投资额（e7）以及生产总值（e8）8个参数的2020年和2021年预测值。预测结果及其精度见表10所示。

表10：8个参数2020年和2021年的灰色预测值及精度表

3.5 人工神经网络模型

误差精度=10，学习次数=10次，神经元个数=8。将e1-e8列数据零均值标准化作为特征数据，将f列数据零均值标准化作为标签数据，使用keras.models库中的Sequential序列模型进行建模。定义3层神经网络，单层人工神经元（隐藏层节点）=12，输入变量（特征值）=8，输出层节点=1，每个神经元用具体的权重初始化，使用relu函数作为激活函数。得出2020年和2021年财政收入的预测值分别为5870.859亿元和6654.844亿元，部分数据见表11，其中f_pred列的数据为预测数据。

表11：部分历史数据及财政收入预测表

图5为真实值与神经网络预测值对比图，从结果中，比较预测值与真实值实现高度吻合。

图5：真实值与神经网络预测值对比图

4 结论

本文通过对某市1998年-2019年地方财政收入数据进行数据挖掘分析，识别出影响因变量的关键特征，使用lasso方法筛选出这些关键特征。使用灰色预测得到这些关键特征的2020年、2021年的预测值。建立神经网络模型，使用历史数据进行训练，最后得出财政收入2020年、2021年的预测值。变量选择方法和神经网络都有多种不同的选择，可将其进行比较和组合作为未来的研究进一步的探索的方向。