一种基于自适应双边滤波的图像降噪算法

林谢卓

（福州大学 福建省福州市 350100）

图像对于沟通交流是十分重要的。生活中，每天都有大量的图片被产生和编辑。然而，在采集、压缩、传输的过程中，由于环境、传输信道等因素的影响，图像会受到噪声的污染，导致部分信息损坏、丢失。因此，图像降噪预处理算法起着至关重要的作用。常见的图像降噪算法有：高斯滤波、各向异性扩散滤波、双边滤波、小波变换、中值滤波等。滤波算法应尽可能实现以下目标：图像纹理简单区域应被平滑，且不存在噪声；图像边缘区域应尽被保留，不被模糊和锐化；尽可能保留原始图像的纹理信息；全图对比度得到保留；不引入人为特征。然而，目标之间在某种情况下是矛盾的，经典的方法虽然去除噪声，但也模糊了边缘，导致图像物体之间难以区分。因此，为解决这个问题，学者提出了基于边缘保护的降噪算法。

近些年来，得益于保护边缘同时平滑图像的特性，双边滤波得到了广泛的应用。它主要应用于图像去噪，如医学图像、电影恢复等方面，及纹理和亮度的分离、色调映射、色调管理、光流计算等。1995年，Aurich and Weule开展了对非线性高斯滤波器的研究。之后，Smith 和Brady在他们所研发的SUSAN 框架中再次发现了该滤波器。在1998年时，Tomasi 和Manduchi将该滤波器命名为“双边滤波”。

双边滤波是一种典型的非线性滤波算法。基于高斯滤波，双边滤波利用强度的变化来保存边缘信息，解决了边缘模糊、在视觉观感上认为重要信息丢失的问题。双边滤波的滤波效果主要取决于两个参数：两个像素的空间邻近性和灰度相似性。当处于纹理较简单区域时，滤波效果主要受空间邻近度的影响；当处于纹理较复杂及边缘区域时，灰度相似度起决定性作用。但本质上，双边滤波是一种邻域像素加权平均的滤波器，会导致图像特征模糊。为进一步优化双边滤波边缘保护和降噪效果，本文对传统双边滤波进行改进，提出一种自适应双边滤波算法，通过经验学习方法获取图像分割的最优块数，对边缘、纹理复杂区域使用小波滤波，对平滑、纹理简单区域使用梯度双边滤波算法。

1 双边滤波

1.1 传统双边滤波

传统双边滤波(Bilateral Filter，记作BF)定义如下：

其中W是一个标准量：

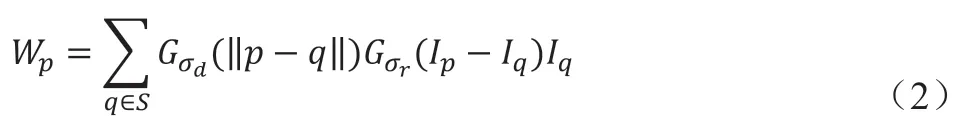
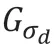
其中，d(p,q)和δ(I(p),I(q))分别为图像量像素点的欧几里得距离及像素的灰度差。

1.2 梯度双边滤波

为了引入图像的局部特征，梯度双边滤波对传统双边滤波的参数进行改进，利用梯度相似度替代灰度相似度，与空间距离构成梯度双边滤波，来对图像的邻域像素进行平均。梯度双边滤波(Gradient Bilateral Fiter,记作GBF)定义如下：

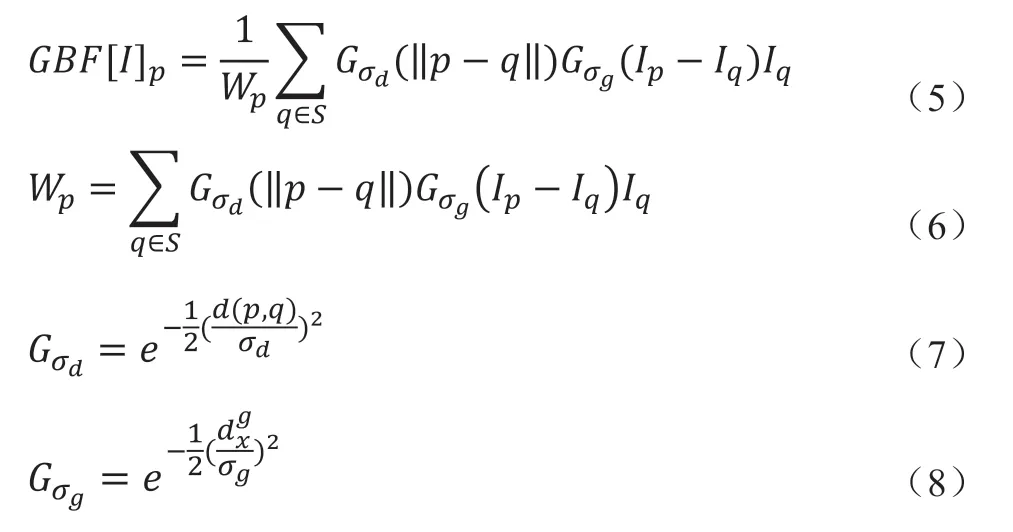
梯度双边滤波的效果主要受到参数空间距离标准差σ和梯度相似度标准差σ的影响。σ的数值大小体现空域的平滑程度，若邻域像素和中心像素距离较近，则分配给邻域像素的权重较大，平滑效果较好；若二者距离较远，则权重变小，平滑效果变弱。该效果相当于普通的高斯滤波，保边效果较差；σ对参与滤波的像素进行筛选，若邻域像素和中心像素梯度值相差较大，则分配给邻域像素的权重较小，对滤滤波结果的影响较小，从而使较多高频信息被保留。

2 自适应双边滤波

当图像处于纹理较为复杂区域时，传统双边滤波不能有效地像小波滤波器一样去除信号不同频率的噪声，尤其是低频噪声。为保护图像特征，本文将结合小波降噪，实现自适应双边滤波图像降噪算法。

2.1 图像分块

假设在图像框架中，噪声的分布是均匀的。由于较为平滑区域的方差大小主要取决于所添加的噪声，纹理较为复杂区域的方差除了包括噪声方差，还包括像素之间的本身差异。因此，平滑区域方差一定小于纹理较为复杂的区域。图像框架可以被划分为大小相同的块，从而更加精细地估计图像方差。太大的块会导致纹理区域之间的重叠，而太小的块会导致样本容量不足，所以精心选择块的大小是十分必要的。文献得出，图像样本快大小为16×16是一个合适的分块选择。

2.2 边缘检测

为了更好地保护边缘，算法利用prewitt 边缘检测算子检测图像框架的边缘部分，对结果图像进行二值化，将较为平滑的、非边缘像素块的布尔数值设置为0，将纹理较为复杂的、处于边缘区域的像素块数值设置为1。计算每个块中数值为“1”像素所占的百分比，并对结果数据排序，取中值作为阈值。百分比大于该阈值的方块看作“边缘方块”，百分比小于该阈值的块看作“非边缘方块”。

2.3 方块滤波

对于小波降噪，当一幅图像中同时含有有效信号和噪声信号时，随着其分解尺度的增加，有效信号的幅值会随之增大，而噪声信号的幅值会随之减小。经过小波多尺度分解的图像，其有效信号分量关联性强，而噪声信号分量关联性很弱。因此相比于双边滤波，小波变换降噪效果更好。对于梯度双边滤波，对参与滤波的像素点是边缘像素点而言，该像素的梯度值与其相邻的非边缘处的梯度值有明显差异，因此分配给该像素点的权重较小，对滤波结果的影响较小，就能较好地保留边缘和细节。

因此，该算法设计对“边缘方块”采用小波降噪，对“非边缘方块”采用自适应梯度双边滤波。对于梯度双边滤波，为达到最佳滤波效果，需要选择合适的σ和σ。根据文献，σ一般介于1.1 到1.5 之间；σ对于噪声标准差比σ更敏感，其值随噪声标准差σ显著变化，与σ关系为σ=3.9796×10σ-1.8432×10σ+0.0023σ+0.0363σ-0.0438σ+0.8682

3 实验结果与分析

为验证所提算法的有效性，将所提算法在Matlab2021上进行仿真实验，向图像中添加不同噪声强度（标准差σ分别为30，40，50）的高斯白噪声，并利用双边滤波、小波降噪、各向异性扩散滤波及所提算法进行图像降噪处理。

3.1 主观分析

图像的最终接收单元是人眼，图像降噪最终的服务对象是人的主观视觉，因此主观评价指的是凭感知者的主观感受来对图像质量进行评价。

选取256×256 Lena 灰度图像和512×512 Barbara 灰度图像作为实验对象，如图1、图2和图3所示。对于降噪处理，传统双边滤波的降噪效果最差，各向异性扩散滤波也仍有部分噪声残留。相较于小波降噪，所提方法保留的边缘细节信息更多。因此，从人眼观察来说，所提算法能够较好地平衡降噪和边缘保护处理效果。

图1：256×256 的Lena 灰度图像去噪结果对比

图2：512×512 的Barbara 灰度图像去噪结果对比

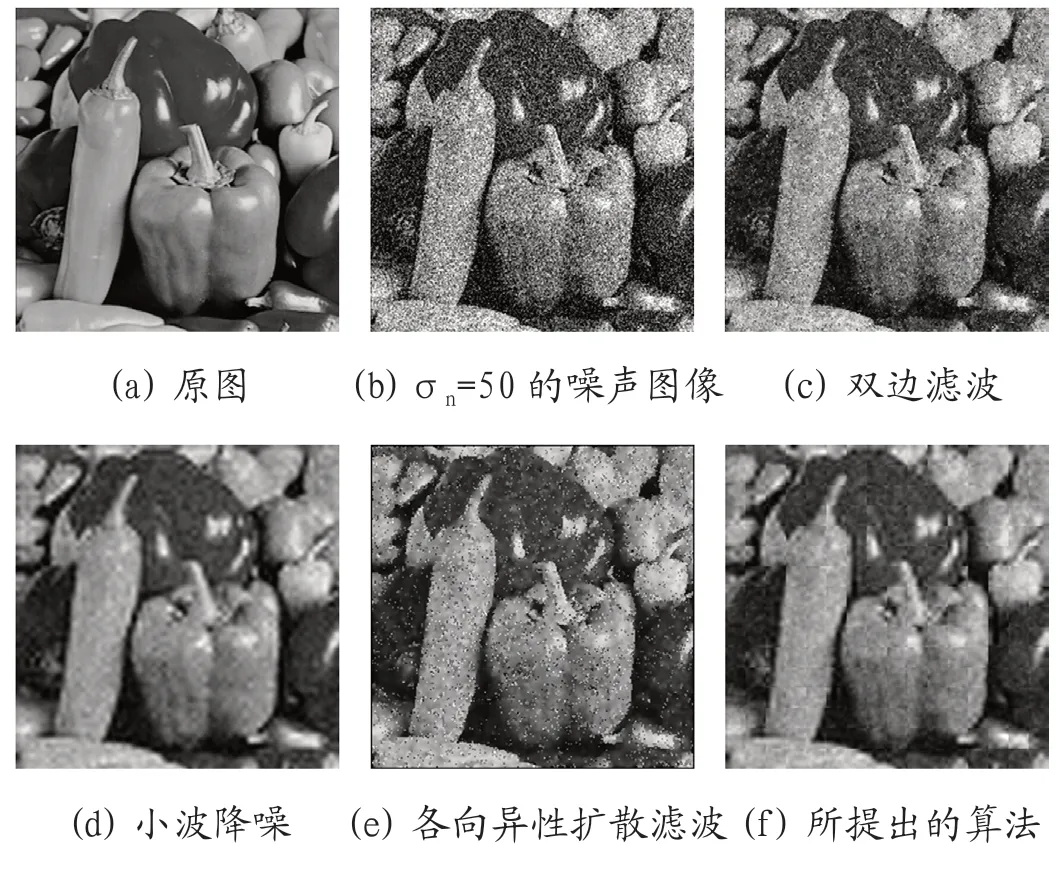
图3：256×256 的Peppers 灰度图像去噪结果对比

3.2 客观分析

对于图像质量的客观分析，通过先计算出被评价图像的某些统计特性和物理参量，常用的是图像相似度的测量，其利用恢复图像与原图像之间等统计误差来衡量恢复图像的质量。常见的物理参量有峰值信噪比(PSNR)、结构相似性(SSIM)、均方差(MSE)等。所提方法采用峰值信噪比(PSNR)和结构相似性(SSIM)，PSNR 代表图像的失真程度，一般介于20dB-40dB 之间，数值越大，恢复图像的失真程度越小，图像质量越高；SSIM 介于-1 到1 之间，数值越大，恢复图像与原图像之间的结构相似度也就越高。

对算法降噪性能的客观分析如表1和表2所示。对于双边滤波和各向异性扩散滤波能，当噪声强度不断增大时PSNR 和SSIM 数值急剧下降，说明其抑制噪声的能力不够稳定。小波去噪和所提算法的PSNR 和SSIM 在不同噪声强度程度数值大小相当，但是回顾对图像的主观评价，所提算法的边缘保护能力和降噪效果优于小波降噪。

表1：不同噪声强度下去噪方法PSNR 对比

表2：不同噪声强度下去噪方法SSIM 对比

综上所述，从主观评价和客观评价两方面来分析，相比传统的双边滤波、小波降噪以及各向异性扩散滤波，所提的方法具有较好的降噪和边缘保护效果。

4 结论

针对传统双边滤波的不足，所提方法先对合理分块，更准确估计图像方差；通过小波变换，更好地去除纹理复杂区域噪声；同时引入梯度双边滤波，有效保留边缘。此外，通过主观和客观分析表明，所提方法较好地提升了传统双边滤波的性能，具有较好地降噪效果和边缘保护效果。

但所提算法还存在一些问题，当处理较小图像时，图像存在块状效应；当处理较大图像时，该算法的粉快处理速度将较慢。因此，未来将继续研究、改进双边滤波参数，降低自适应双边滤波图像降噪处理的时间复杂度。