深度残差对冲网络及其在滚动轴承故障诊断中的应用

康玉祥，陈果,*，尉询楷，周磊

1. 南京航空航天大学 民航学院，南京 210016 2. 北京航空工程技术研究中心,北京 100076

滚动轴承是航空发动机支撑系统和传动系统的关键部件，因其工作环境的复杂和多变，极易发生故障，且其寿命难于准确预测。航空发动机滚动轴承故障严重危及发动机使用安全，已成为制约中国航空发动机技术发展、影响战斗力生成的重大技术“瓶颈”。对于航空发动机，即使很轻微的滚动轴承故障也可能导致整个飞机出现空中停车，甚至发生坠机事故。因此，尽早有效地对航空发动机滚动轴承进行故障诊断极其重要。

当前以小波分析、傅里叶变换和机器学习为代表的传统故障诊断方法主要有人工提取特征、故障诊断两个步骤。该类方法首先从一维原始信号中提取数据特征。然后采用诸如主成分分析法(Principal Component Analysis，PCA)、线性判别分析(Linear Discriminant Analysis，LDA)等数据降维方法对所提取的冗余特征进行剔除。最后将经过降维处理的特征数据作为支持向量机(Support Vector Machine，SVM)、多层前馈网络(Back Propagation，BP)等模型的输入，对算法进行训练，获得故障诊断模型。该类方法的主要问题在于其过度依赖专家经验，对数据降维导致有用的特征被剔除，影响测试精度。

深度学习因其可实现端到端的学习，省略了人工提取特征的过程，可自动建立特征至类型的非线性映射，因此大量的深度学习算法被越来越多地应用于滚动轴承故障诊断。雷亚国等将深度迁移学习用于滚动轴承故障诊断中，很好地识别了机车轴承的健康状态。Wen等对深度迁移自编码器进行了改进，并将其用于轴承故障诊断，精确地诊断出了轴承的故障。张向阳等基于卷积神经网络(Convolutional Neural Networks，CNN)成功地识别了基于机匣测点的滚动轴承故障。Guo等提出了一种自适应学习率的改进卷积神经网络，并将其用于滚动轴承故障诊断，在故障尺寸大小识别和故障类型诊断中都取得了很好的效果。Lei等将长短期记忆网络(Long Short-Term Memory，LSTM)用于风电机组的轴承故障诊断，取得了很好的诊断效果。Zhang等提出了一种改进深度置信网络(Deep Belief Network，DBN)算法，并在滚动轴承的故障诊断试验中取得了良好的效果。Wang等提出了一种多层监督自编码器模型，该模型有效地提高了故障测试精度。Huang等提出了一种多尺度级联卷积神经网络用于轴承的故障诊断。Khorram等以原始加速度振动数据(时域特征)为输入，提出一种端到端的故障检测方法，该方法具有检测精度高、收敛速度快的特点。然而以上基于深度学习的滚动轴承故障诊断模型虽取得了很好的诊断效果，但仍然存在难训练、泛化能力差等一系列问题。因此近年来深度残差网络(Deep Residual Networks，Resnet)被诸多研究者用于滚动轴承故障诊断。

深度残差网络于2016年被提出，该网络模型在随后的Imagenet数据大赛中以压倒性的优势取得了当年的冠军。目前，该模型被大量地用于滚动轴承故障诊断。如Wen等提出了一种新的50层残差网络模型模型，并将时域故障信号转换为RGB图像作为所提模型的输入，实现了轴承故障的精确诊断。Du等以短时傅里叶变换(Short-Time Fourier Transform，STFT)的时频图为输入，提出了基于Resnet的变工况故障诊断方法。虽与以CNN为代表的深度学习方法相比Resnet具有很好的效果，但随网络深度增加、参数量增大，也同样存在诸如训练速度慢等不足。

有鉴于此，首先对残差块进行改进，提出对冲结构的思想，以期在保证网络收敛精度的同时提高网络训练速度。然后，将胶囊网络中的Squash函数用于全连接层，从而防止网络输出值过大导致的损失梯度发散问题。最后，对所提深度残差对冲网络(Deep Residual Hedging Network，DResHnet)在两组滚动轴承轴承数据集上进行验证，以期表明所提方法的正确性和有效性。

1 Resnet

为解决随深度增加神经网络出现性能退化的问题，He等将残差块概念引入Resnet。图1为残差块结构，其中为第个残差块的输入；()为经过卷积、批归一化、激活函数的残差映射输出；()为恒等映射输出，该映射的目的是使输入和()具有相同尺寸，()=表示为残差直连结构；为Relu激活函数，其表达式为

(1)

式中：为激活函数的输入。

由图1中残差结构块可知，多个残差块连接的网络数学模型为

+1=+(,)

(2)

式中：为残差块模型的权重参数。

第层的输出为

(3)

根据文献[17]可得网络第层的梯度为

(4)

式中：为实际网络的实际损失值。

图1 残差块结构Fig.1 Residual structure

式(4)表明通过多个残差块的串联，Resnet在误差反向传播的过程中能保证梯度大于0，从而避免网络出现梯度消失的问题。

虽然Resnet被证明是一种精度较高的网络，但随网络深度增加，网络参数也随之增多，导致网络收敛速度慢、难训练。因此在保证网络精度的前提下，需解决训练速度慢的问题。以18层残差网络为基础，对Resnet进行改进。

2 深度残差对冲网络

2.1 深度残差对冲网络结构

深度残差对冲网络如图2所示，图2中() 和()分别为第(=1,2,3,4)层堆叠卷积对冲操作和恒等映射后的输出。输入为滚动轴承一维时域信号通过快速傅里叶变换(Fast Fourier Transform，FFT)的频谱图，输出为滚动轴承故障类别。

图2 深度残差对冲网络Fig.2 Deep residuals hedging network

DResHnet主要由4层堆叠卷积对冲结构块(Stack Convolution Hedge Structure，SCHC)、4层恒等映射块、对冲操作、Squash压缩函数、Fn全连接层等部分组成。

试验中采用的GPU为NVIDIA GTX1660 6G、i5-9600K处理器、8 G内存、运行系统为Windows 10、编程语言为Python 3.7、深度学习框架为Tensorflow 1.15。设置批处理样本量为64、迭代轮数为100。本文模型参数设置和Resnet18类似，具体参照如表1所示。表1中的“×4”代表堆叠卷积对冲结构中有4个卷积层；“×1”代表恒等映射块中有1个卷积层；输入层中的“×2”代表输入经过2个卷积层后进行对冲操作；中间层中的“×2”表示由两个堆叠卷积对冲结构块组成。Resnet18和Resnet34同样采用经典的结构，之所以选择Resnet18和Resnet34是因为所提算法是基于Resnet18的结构改进而来，而改进后的参数量和Resnet34相差不多，所以选择Resnet18、Resnet34作为比较算法精度和算法收敛速度的依据。

表1 深度残差对冲网络信息Table 1 Information of deep residual hedging network

2.2 堆叠卷积对冲结构

传统的Resnet需较深的网络层才能达到很好的分类精度，这就需要多GPU的硬件条件才能完成网络训练。而Inception结构被证明是一种有效提高网络效率的方式，因此为能在单机单GPU卡上完成网络训练，同时提高网络的精度与速度，借助Inception堆叠的思想提出如图3所示的堆叠卷积对冲结构块。

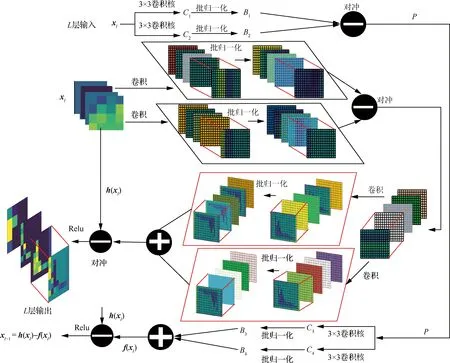
图3 堆叠卷积对冲结构块Fig.3 Stack convolution hedge structural blocks

图3所示的算法具体步骤如下：

通过两个并行的、不同参数的堆叠卷积核对相同的输入进行特征提取。

输入经堆叠卷积处理后得到卷积结果、，然后进行批归一化操作，防止“梯度爆炸”现象。

对步骤2之后的结果进行对冲操作(对批归一化之后的输出特征图、作差)，获得对冲操作(Hedging Processes)结果。对冲操作是为了筛除两路卷积学习到的相同特征，保留不同的特征，以便后续的网络层能对之前没有学习到的特征进行学习，而无需重复学习相同的特征。

图4为训练过程中两个特征图的对冲操作结果，图4(c)中结果显示对冲操作可对特征图起到增强和增加敏感特征的效果(图4(c)中敏感特征点多于图4(a)和图4(b))。对冲操作可增强特征图的稀疏性，从而达到加速网络收敛的目的。

对对冲后的剩余图像进行同样的堆叠卷积，获得卷积结果、。

对卷积后的数据进行批处理操作输出特征图、。

对步骤5之后的输出进行堆叠相加(防止因对冲后图像值过小而网络无学习能力的现象发生)得到输出()。

将恒等映射后的输出()和残差映射后的()进行一次对冲操作。

采用Relu函数进行激活，得到输出+1。

图4 对冲操作结果Fig.4 Hedging processes results

图3中的对冲结构和传统的对同一特征进行连续卷积不同，其本质是将不同的特征分配给各个卷积层进行特征提取，用于实现学习图像特征的目的。

由图2及SCHC结构可知式(5)成立：

(5)

根据式(5)可得

-(--1))+(-1)+1--1

(6)

式中：-为第-层的输入；为网络总层数；为图2中从右往左数第层；为图2中从右往左数第层。模型的各层和输入之间全部进行了残差连接，可有效预防网络性能退化现象。

2.3 恒等映射块

传统的Resnet是由多个残差块串联而成的，这就使后续网络层不能很好地利用初始的输入特征。此外考虑到不同状态下样本特征之间细微的差别，经过串联后往往会将这些差别映射至相同的区域，导致网络无法完成精确分类。为此将起始输入经特定的恒等映射模块与2.2节中提出的堆叠卷积对冲结构块结合，形成新的对冲模块，图5 为第层的恒等映射块和堆叠卷积对冲结构块形成的新对冲结构。

图5中卷积核大小为3×3；池化层采用2×2的最大值池化，步长为2。经过对原始图像进行恒等映射和2.1节中的SCHC组成新的对冲结构，使下一层可同时接收来自原始图像的部分特征和上层对冲结构块的输出，从而强化了各层学习特征的能力。

图5 恒等映射块Fig.5 Identity mapping block

2.4 Squash函数及网络训练

Squash函数于2017年由Hinton等提出，目的是将向量中各个元素均压缩至[0,1]区间内，且压缩后向量和原向量的方向角相同。因卷积操作中具有累加的性质，为防止全连接层的输入向量过大，首先在全连接层前引入Squash函数对输入向量进行压缩，然后计算全连接层的输出，最后采用Softmax进行分类。

采用如式(7)所示的Squash函数计算第1层全连接层的输入：

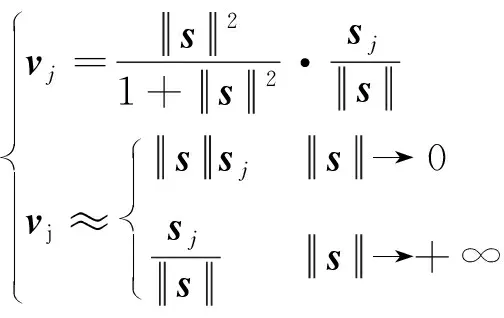
(7)

式中：为经过压缩后的第个元素；为由卷积结果转换的一维向量；为中的第个元素。

采用Relu函数计算全连接层的输出：

(8)

式中：为全连接层第个神经元的输出；为全连接层第个神经元和第个输入之间的权重；为输入元素的个数；为偏置；为激活函数。

采用如式(9)所示的交叉损失函数，优化算法为Adam算法，学习率为0.000 1。

(9)

式中：为分类类别总数；为真实样本标签；为Softmax分类函数(如式(10)所示)的输出，表示第个类别的概率。

(10)

式中：为自然常数。

3 模型验证

为验证DResHnet模型的性能，选取Mnist和Cifar-10数据集进行试验，其中Mnist数据集为60 000张28×28的手写数字图像，主要用于验证算法快速收敛的特点；Cifar-10数据集包含大小为32×32×3的10种类别图像，用于验证算法快速收敛和高精度的特点。在相同试验条件下对DResHnet、Resnet18和Resnet34的结果进行对比验证。

3.1 Mnist数据集

图6为在Mnist数据集上的训练误差变化曲线。以达到99%的训练精度为目标，图6中同时给出了每种算法收敛到99%精度的计算时间和相应的迭代次数。DResHnet在34次迭代时收敛到99%的精度，计算时间为952.63 s；Resnet34的计算时间为1 575.11 s，迭代次数为57次；Resnet18的迭代次数为99次，计算时间为1 263.24 s。相比其他两种算法，DResHnet收敛速度更快。

图6 Mnist数据集试验结果Fig.6 Test results of Mnist data set

3.2 Cifar-10数据集

采用交叉验证的方式将3.1节中的3种算法用于对Cifar-10数据集的分类。每种算法分别计算10次，图7为3种算法的10次测试结果。取10次中最好的测试结果为最终测试精度和相应的训练时间进行平均作为计算时间，表2为测试精度和计算时间试验结果。

图7和表2中结果显示，DreHnet较其他两种算法的测试精度提高了约2%，且计算时间更少。

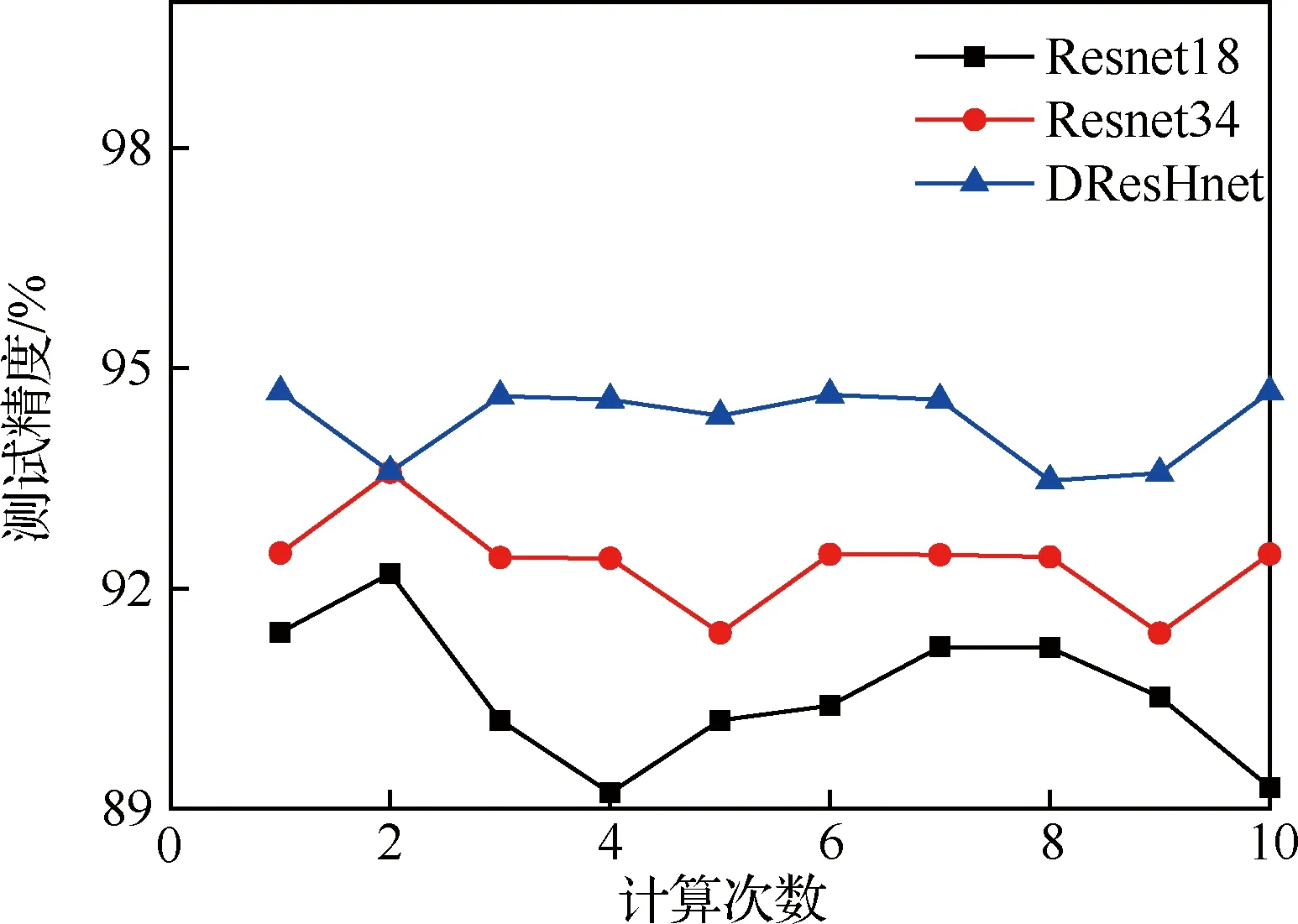
图7 Cifar-10数据集10次试验结果Fig.7 Test results of 10 trials on Cifar-10 data set

表2 Cifar-10数据集最终试验结果Table 2 Final test results of Cifar-10 data set

通过对比Mnist和Cifar-10数据集上的试验结果可很容易地看出，DResHnet在保证精度的前提下具有更快的收敛速度，这也和算法改进的初衷一致，同时也验证了算法理论上的可行性和准确性。

4 滚动轴承故障诊断实例

为验证DResHnet在滚动轴承故障诊断中的有效性。首先，选择研究者普遍采用的美国凯斯西储大学的滚动轴承故障诊断数据集进行故障诊断验证。其次，将DResHnet应用于带机匣的航空发动机转子试验器滚动轴承故障试验数据诊断，并进行多种方法的对比验证。

4.1 美国凯斯西储大学滚动轴承故障试验数据诊断

选择美国凯斯西储大学滚动轴承故障诊断数据集的驱动端数据，其相应的轴承型号为SKF6205，选择数据采样频率为12 kHz。轴承共有内圈、外圈、滚动体3种加工缺陷故障，连同正常状态共4种状态。为确保试验数据为二维图像输入，且避免人为对时序数据按一定的方式进行数据重构。首先，将原始各个类别数据按7∶3的比例划分训练和测试集。按数据采样频率，采用数据增强方法以一定的步长对时域振动信号进行采样，如图8所示，其中步长为1 000个点，样本点数为12 000。然后，对每组样本进行FFT得到频谱图。最后，将获得的频谱图直接保存为png格式的图形文件，图形文件大小为32×32×3，图9为转换后的频谱图。

图8 振动信号采样Fig.8 Vibration signal sampling

图9 轴承信号的频谱图Fig.9 Spectrum diagram of bearing signal

为验证所提算法不受负载、转速、损伤大小的影响。试验数据集包含各种不同条件下的滚动轴承故障数据。通过数据重采样和FFT操作后，数据集包含的样本文件信息如表3所示。其中外圈中不包含0.711 2 mm的损伤样本。

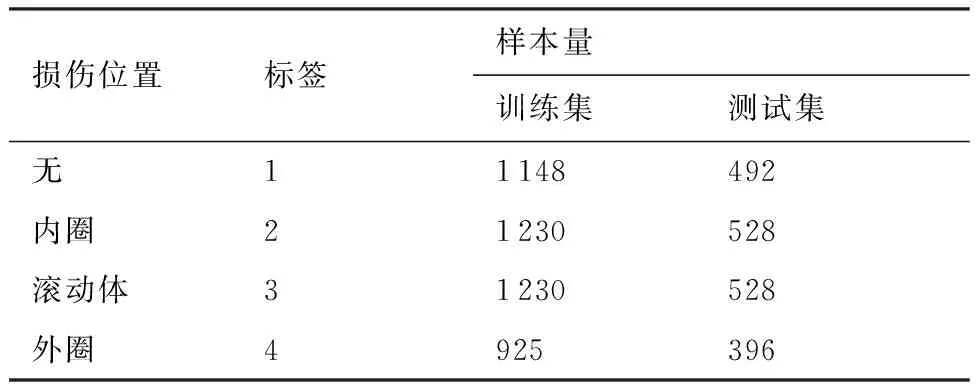
表3 数据集样本信息Table 3 Sample information of data set

为验证所提算法在速度和精度方面的优势，比较所提算法与CNN、Alexnet、Resnet18、Resnet34网络的故障诊断结果。其中，CNN采用4层卷积和池化的网络结构，卷积核大小为3×3；Alexnet采用经典的结构；Resnet18和Resnet34与第3节中的结构相同。

图10为各个模型的收敛精度曲线。试验中每种方法均进行10次计算。取多次计算的平均收敛精度进行比较，表4为收敛精度比较结果。

图10 故障分类结果Fig.10 Fault classification results

表4 模型收敛精度比较Table 4 Comparison of model convergence accuracy

表4中数据表明与残差结构相比，传统的卷积网络收敛速度很慢。DResHnet和Resnet34算法的收敛精度均达到了100.00%，且DResHnet的收敛速度最快。

图11为DResHnet和Resnet18、Resnet34算法在测试集上收敛速度的对比结果。图11显示在测试集上DResHnet相较Resnet18和Resnet34在达到99%测试精度时收敛速度至少提高了1/3。DResHnet在第一次达99%测试精度时迭代次数为600，而计算时间为181.64 s；Resnet34算法在迭代1 100次后达99%收敛精度，计算时间为498.66 s；而Resnet18达99%计算精度的迭代次数为1 200，计算时间为273.23 s。对比计算时间可知所提对冲结构可加快收敛速度、提高算法的精度。

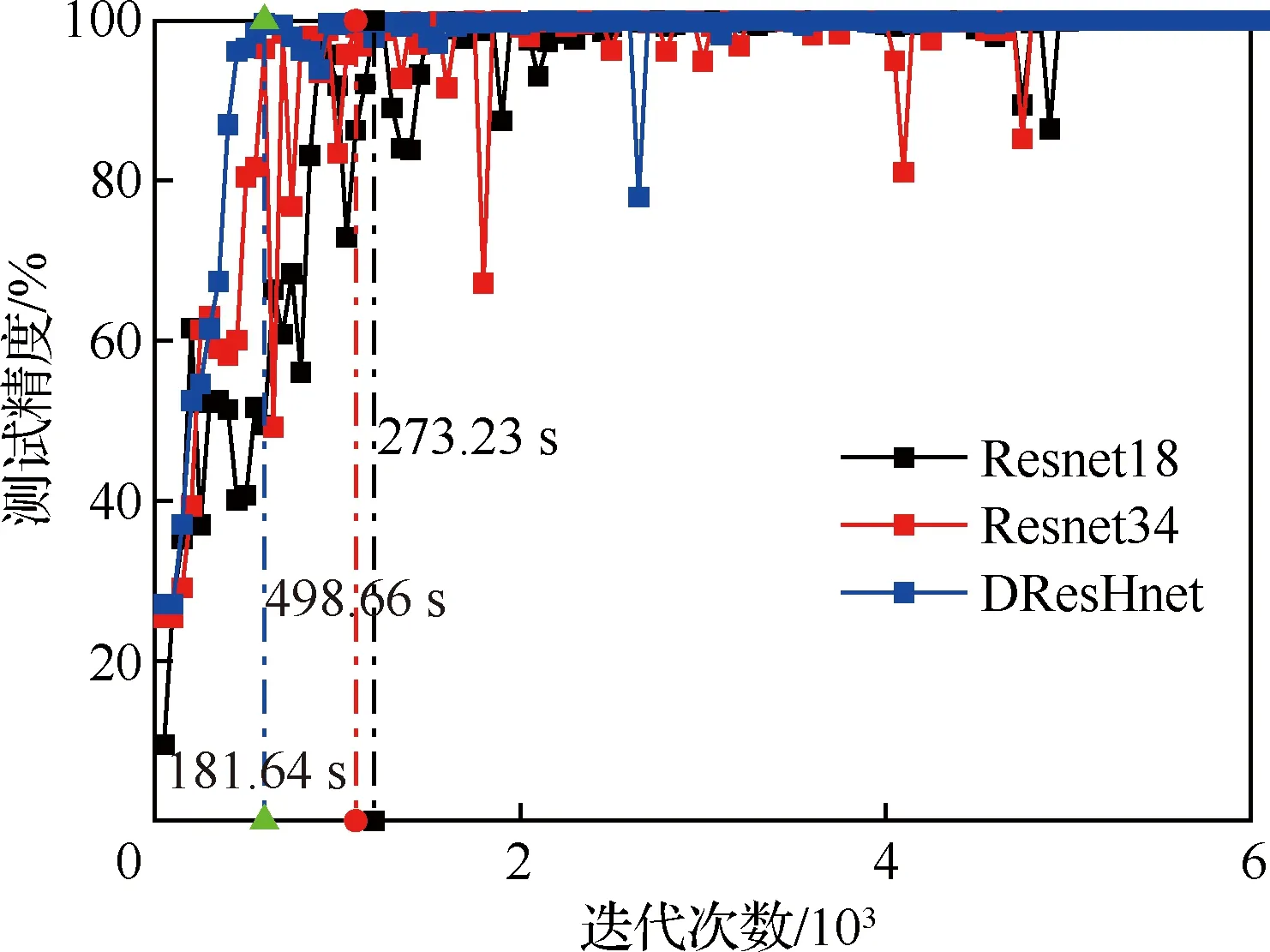
图11 故障测试结果Fig.11 Fault classification test results

为进一步说明本文算法的诊断效果，表5列出了不同故障类别的测试精度结果和相应分类结果的混淆矩阵。结果显示对于单类别诊断，Resnet34和DResHnet均达到了100.0%的最高测试精度，其次分别为Resnet18模型、Alexnet、CNN，这也和图10和表4的结论相一致。

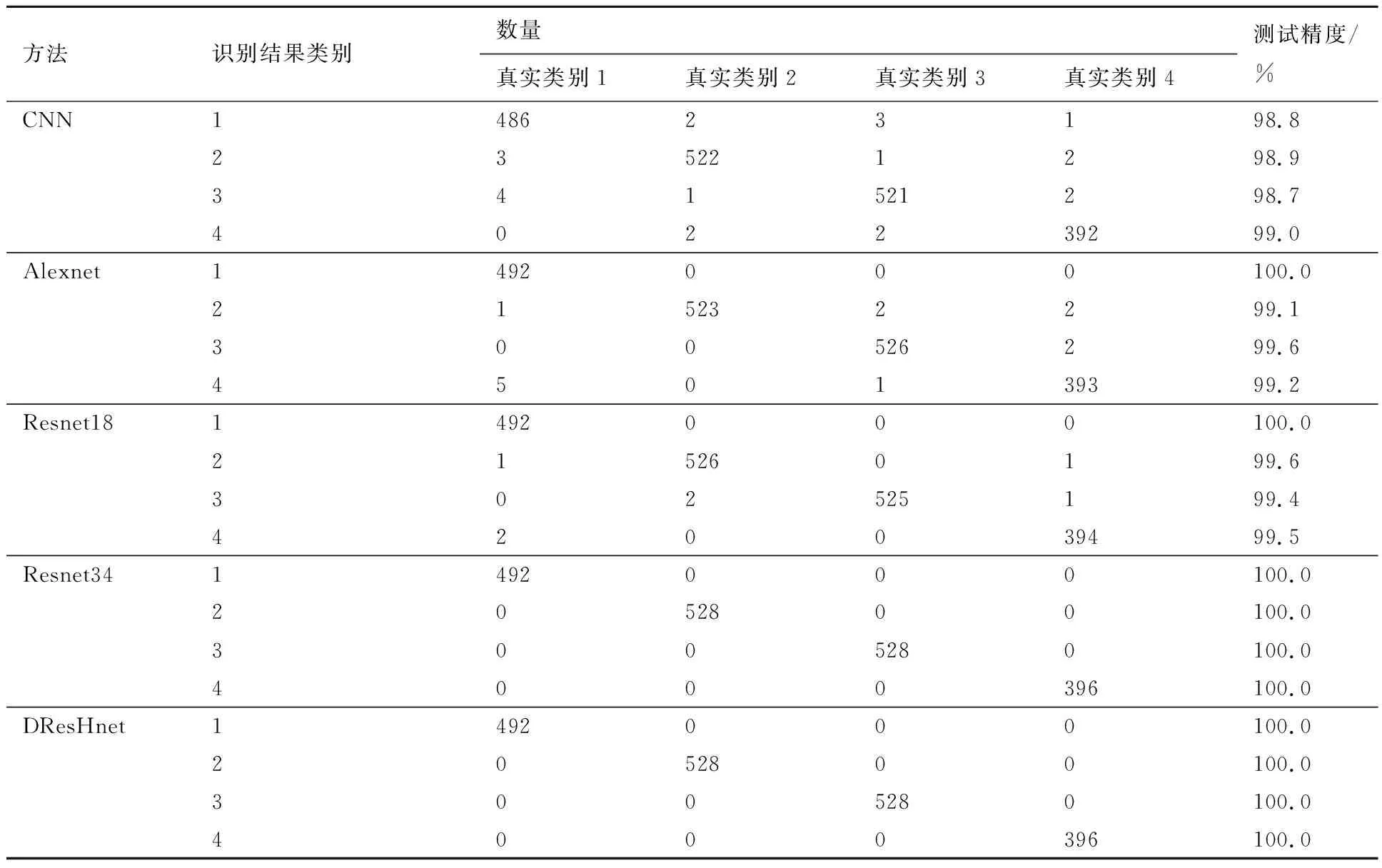
表5 西储大学数据测试结果信息Table 5 Case western reserve university data test result information

4.2 带机匣的航空发动机转子试验器滚动轴承故障诊断试验

基于机匣信号的航空发动机轴承故障试验是在如图12所示的平台上完成的，该试验平台为以1∶3比例仿制的某型真实发动机。试验平台能有效反映航空发动机振动信号在传递过程中的衰减特性，试验中采用的是轴承型号为6206的单列深沟球轴承。在试验过程中利用电火花切割方式加工了如下故障缺陷：外圈和内圈故障分别为6 mm 宽的裂痕，滚动体故障为半径0.5 mm、深度2 mm 的凹陷。具体缺陷如图13所示。

图12 航空发动机实验器Fig.12 Acro-engine rotor tester

图13 滚动轴承故障部位Fig.13 Fault positions of rolling bearing

试验中采用B&K4805振动加速度传感器、NI USB9234数据采集器，采样频率为10 240 Hz，样本数据点为8 192。试验转速为1 500、1 800、2 000、2 400 r/min。传感器安装位置如图12所示。根据1∶4的比例划分测试集和训练集后，将采样数据点经FFT后转换为png格式的图像数据文件。将所提算法用于基于机匣信号的航空发动机轴承故障诊断，同时和Resnet18、Resnet34进行对比，结果如图14所示。针对相同数据集，本文方法的测试精度远高于文献[2]的CNN和SVM方法，如表6所示。

图14和表6的结果显示DResHnet测试精度为100.00%，相比其他几种算法具有更高的测试精度，且和同类型的Resnet18和Resnet34算法相比具有更快的收敛速度，这和3.1节中的结论一致。结果表明本文算法在基于机匣测点的滚动轴承故障诊断中具有更加明显的优势，能有效提高故障诊断精度，且算法具有很好的泛化能力。 限于篇幅，表7列出了部分算法不同故障类别的测试精度和相应分类结果的混淆矩阵。表7中的数据含义和结果显示对于单类别的诊断DResHnet算法能实现100.0%的诊断结果，表明该模型在进行故障诊断方面的优势，也进一步说明了所提模型的准确性。

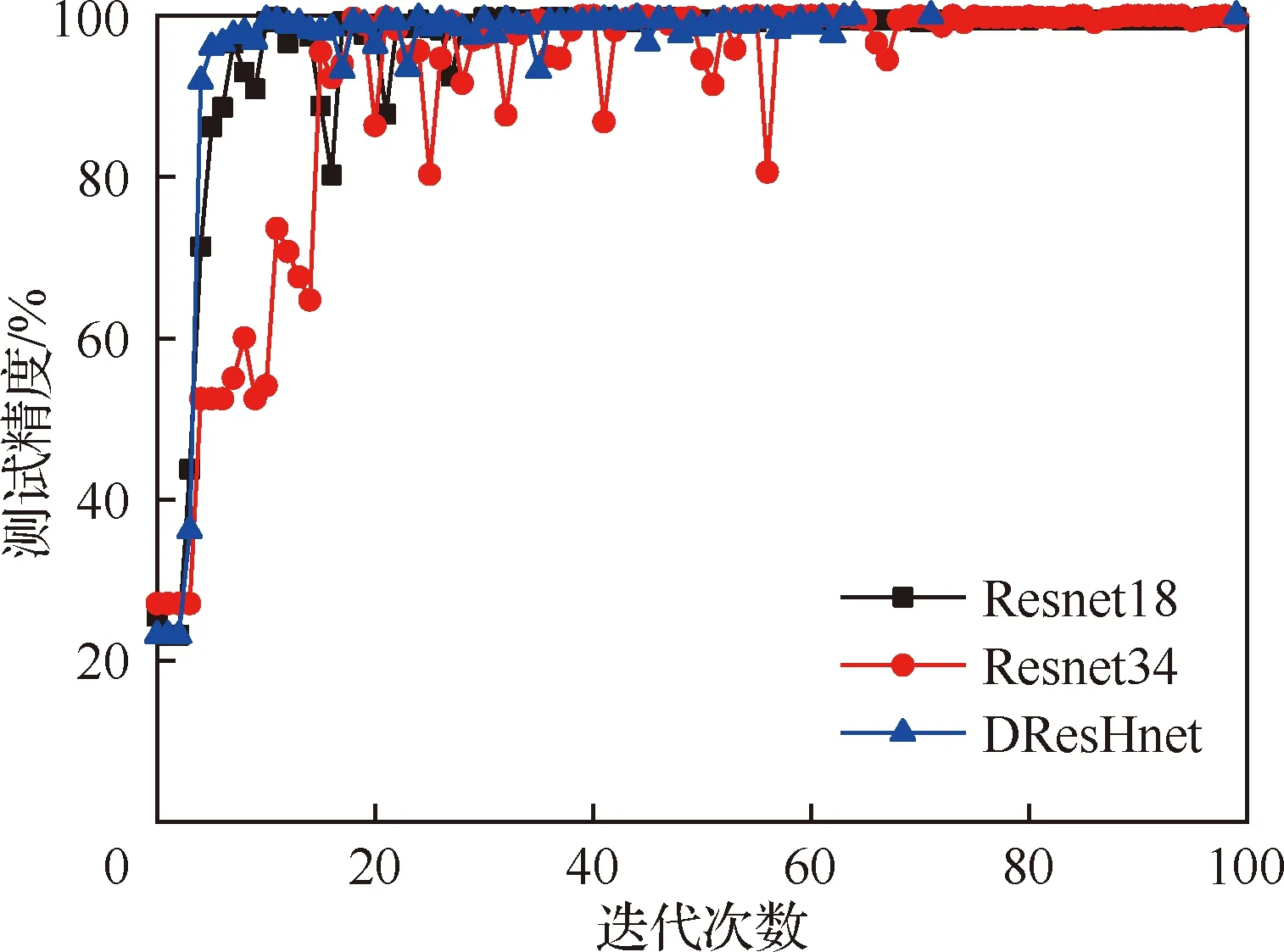
图14 试验数据故障诊断测试精度Fig.14 Experimental data fault diagnosis test accuracy

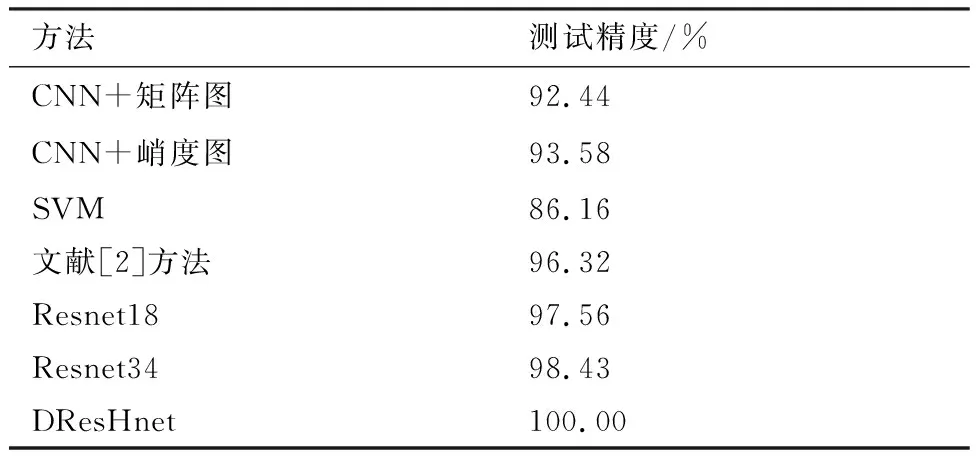
表6 发动机轴承故障诊断测试精度比较

5 结 论

提出了一种名为深度残差对冲的网络(DResHnet)，并介绍了所提网络的基本模型结构。在将其应用于轴承故障诊断的过程中，直接以FFT所得的归一化频谱图为输入，避免了人为设计输入数据的过程。在标准数据集和发动机机匣测点实验数据集上所提算法都展现了故障诊断的优势。这既充分证明了DResHnet具有较高的测试精度与较快的收敛速度，也表明该网络具有很好的应用前景。

表7 测试结果信息Table 7 Test result information