三次和二次总成本函数的特性以及期望本利解的互换
毛克宁
(广东理工学院经济管理学院 广东肇庆 526070)
在经济管理中,成本和利润是最为基本和重要的问题,两者密切关联,而成本问题往往更为基础。关于成本的研究论题十分广泛,有着丰富的研究结果,如结合计量回归方法对涉及污染与治理的成本函数模型的研究[1],从不同领域或视角对成本的理论和实际问题的研究等[2-3]。研究成本需要进行量化分析,如果企业能找出自身生产经营中成本的变动规律,统计归纳出成本函数,则可以更为合理地做出科学决策,如涉及二次成本函数的关于企业市场竞争的研究[4-5]。该文第一部分主要阐述经济学中较为常见的三次总成本函数两个应有的重要特性,其次阐述更为简单的二次短期总成本函数的一个重要特性,这样可以便捷地检判一个三次总成本或二次短期总成本函数是否有误。当企业面临的需求量为随机需变量时,理论上需要考虑期望利润最大化或期望成本最小化问题,但这是两类不同的问题。根据传统经济学理论,利润最大化与成本最小化问题就一般意义而言两者并不等价。对于需求量为随机需变量的情况,一类典型问题就是报童问题。一些文献指出报童问题期望损失或期望成本最小化与期望利润最大化的求解可以互换,这无疑给两类问题的求解带来了一定的便利,但却引发了这与传统经济学理论是否相符的思考。文献[6-7]指出离散型需求量报童问题期望损失最小与期望利润最大的进货量是一致的,文献[8]证明了前述期望总损失最小化的进货量其实是与期望会计利润最大化的进货量相同,并指出其期望总损失既不是报童问题的期望显性成本也不是期望经济成本。文献[9]阐述证明了连续型随机需求量报童问题的期望成本最小化模型与期望利润最大化模型具有等价性,在一定条件下它们有相同的最优解。但根据文献[8]可知文献[9]所述的“期望成本”不是期望显性成本和期望经济成本,而是类似于文献[6-7]的期望损失,其期望利润是期望会计利润。该文第二部分对报童问题的期望经济成本最小化进货量关系式和期望利润最大化进货量关系式及其互换性做了严格推导论证。
1 三次和二次总成本函数的特性
1.1 三次总成本函数
该文以企业短期总成本和长期总成本在各自的产量范围内皆随产量增大而严格单调增加为论述前提,且仅以企业的三次或二次总成本函数的导函数作为边际成本函数,而非其他形式。
需指出,若函数h(x)在区间(ab)严格单调增加,对于x0(ab),x0 且x0+x(ab),必然有,当导数h′(x0)存在时,h′(x0)=,即有可能h′(x0)=0。对于可导的短期或长期总成本函数TC(Q),对于其产量区间内部的特定产量Q0,由导数得出的MC(Q0)=TC′(Q0)也是非负的,这是由其经济含义决定的。对于经济中的其他边际量另当别论。
已知微分学中的一个定理:“若函数f(x)在区间[ab]连续,在区间(ab)可导,则f(x)在[ab]单调增加的充分必要条件是f′(x)≥0,x(ab)”。不难得出后续结论:若函数f(x)在区间[0+)连续,在区间(0+)可导,则f(x)在[0+)单调增加的充分必要条件是f′(x)≥0,x(0+)。
命题1 三次函数在一个区间单调增加与其在该区间严格单调增加是等价的。特定的三次函数f(x)=ax3+bx2+cx+d(a>0,b<0)在区间[0+)单调增加的充分必要条件是b2≤3ac。
证明 由于三次(实系数多项式)函数最多有3个实根,易知三次函数在一个区间单调增加与其在该区间严格单调增加等价。根据前述定理的后续结论知,f(x)=ax3+bx2+cx+d(a>0,b<0)在区间[0+)单调增加的充分必要条件是其导函数f′(x)=3ax2+2bx+c≥0,x(0+),即4b2≤12ac,亦即b2≤3ac。【证毕】
三次长期总成本函数LTC(Q)=αQ3+βQ2+γQ的产量Q可在区间[0,+∞)变动,其三次项系数为正值,即α>0。因若α<0,必有,则与总成本随产量增大而严格单调增加矛盾。三次短期总成本函数TC=aQ3+bQ2+cQ+FC(FC为固定成本)的产量Q变动不超出从零到短期最大产量的有限区间。当产量接近于短期最大产量时,短期总成本的增长率MC的增长率MC'(Q)不可能是严格单调下降的,故MC″(Q)=6a非负,于是a>0,因此三次短期总成本函数的三次项系数为正值。
命题2 对于三次短期总成本函数TC=aQ3+bQ2+cQ+FC(a>0),一般地,二次项系数b<0,一次项系数c>0[10-12],且b2≤3ac。
对于三次长期总成本函数LTC=αQ3+βQ2+γQ(a>0),二次项系数β<0,一次项系数γ>0[10-12],且β2≤3αγ。
证明 对于短期总成本函数TC=aQ3+bQ2+cQ+FC(a>0),根据平均可变成本AVC随产量增大而先降后升的一般特性[10-12],作为二次函数的AVC=aQ2+一般应有正的最小值点,故一般有b<0。由于MC=3aQ2+2bQ+c=,而,且有,于是b2≤3ac,c>0。
对于长期总成本函数LTC=αQ3+βQ2+γQ(α>0),根据长期平均成本LAC随产量增大而先降后升的特性,LAC=αQ2+βQ+γ有正的最小值点,可得出β<0且γ>0,由命题1,有β2≤3αγ。【证毕】例如:若假设某企业的短期总成本函数为TC=Q3-3Q2+2Q+70,则(-3)2>3´1´2,与命题2不符。说明该短期总成本函数TC的假设有误。
1.2 二次短期总成本函数
命题3 二次短期总成本函数TC=aQ2+bQ+FC的二次项系数为正,一次项系数非负[10-14],即a>0,b≥0。
证明 假设所述企业的短期最大产量为QM,则当产量Q趋近于QM时,TC的单位增长幅度越来越大,其函数曲线向右上方的倾斜越来越陡峭(上凹),当产量Q接近于QM时,作为总成本TC变化率的边际成本MC是单调增加的,MC的导函数MC'(Q)=(2aQ+b)'=2a非负,从而a>0。由于若b<0,则与产量Q=0 时总成本TC最小矛盾,故b≥0。【证毕】
对于二次短期总成本函数TC=aQ2+bQ+FC(a>0,b≥0),平均可变成本AVC=aQ+b随产量的增大而严格单调增加,并非先降后升。
1.3 回归方法与三次和二次总成本函数
企业的短期总成本函数往往不是现成的,也不是一成不变的,可以根据实际数据利用统计学方法估计得出。
例1 通过表1的产量和短期总成本具体数值[11],运用回归方法得出估计的三次或二次短期总成本函数[15]。

表1 短期总成本表
解析:(1)利用Excel软件,由表1通过回归方法求得估计的三次短期总成本函数

与命题2相符。
(2)利用Excel 软件,由表1 通过回归方法求得估计的二次短期总成本函数

与命题3相符。
根据已知样本将得出的三次和二次短期总成本函数的估计值进行对比,其数据具体见表2。

表2 三次和二次短期总成本函数估计值对照表
从表2对照表来看,关于短期总成本的估计,所求出的三次总成本函数优于二次总成本函数。
2 期望成本与期望利润解的互换性
期望成本与期望利润解的互换性有3 点需要说明,具体叙述如下。
一是该文中所述“经济成本”[16]与文献[8]中所述“总成本”[10]都是指“显性成本+隐性成本”,只是称谓不同,但称为经济成本更加规范,以免和经济学中常用的短期总成本概念混淆。二是该文中的隐性成本涉及两种情形,一种是将供不应求导致卖者的收益损失作为隐性成本,另一种是将供不应求导致卖者的利润损失作为隐性成本[8]。两者的含义有所不同,后者扣除了由于进货量不足而节省的购进价,而前者没有将其扣除。在计算经济利润时按后者考虑隐性成本更为合理,但前者更符合一些经济学教科书中的定义,尤其是基于存储的经济成本模型和经济利润模型及其求解会相对简单。三是可以看出在参考文献[8]中所有关于报童问题期望利润的阐述对于随机需求量可能的取值个数n≥2 仍然成立,故该文取n≥2,这不影响对文献[8]的有关结论引用。
2.1 报童问题描述和已知结果
为阐述便利,该文再次给出文献[8]的报童问题描述以及符号表示。报童问题描述[6-7]:卖者每天购进货品后零售,买者一天对该卖者商品的需求量r(单位数)为离散型随机变量。卖者以每单位c元购进货品,并以每单位p元出售(p>c>0);对未售出的商品进行处理,每单位亏损u元(0 假设:(1)需求量r可能的取值为rj(j=12…n;0 ≤r1 (2)卖者每天一次性购进货品单位数为Q,决策变量Q不是随机变量,但其可取值也为rj(j=12…n)[6-7]。 (3)卖者每天的初始存货量为零。Q为多少时卖者一天的期望利润最大? 根据问题描述得出,卖者进货量为Q的(期望)显性成本为cQ; 由文献[8]知,W(Q)最大化的进货量rm可由下面式(1)得出 根据Q的取值假设,使得期望显性成本cQ最小化的进货量为Q=r1,而式(1)中的rm不一定是r1。故就一般意义而言,期望显性成本最小化进货量关系式与期望会计利润最大化进货量关系式不同,两者不可互换。 若卖者进货量不足,则供不应求导致收益损失的期望为 将式(2)作为进货量为Q的期望隐性成本(与文献[8]中关于期望隐性成本的定义有所不同),这里是将供不应求导致卖者的收益损失作为隐性成本。在期望隐性本定义为式(2)的情况下,卖者进货量为Q的期望经济成本为 在期望隐性成本定义为式(2)情况下,卖者进货量为Q的期望经济利润为 综合式(3)和式(4)可知,在期望隐性成本定义为式(2)情况下,报童问题的期望经济成本最小化进货量关系式与期望经济利润最大化进货量关系式不同,两者不可互换。需要指出的是,上述显然不是进货量为Q的期望显性成本,并且也不是进货量为Q的期望经济成本。这是因为中含有v=c-u,即实际上含有外生变量u,而期望经济成本G(Q)表达式中是不含u的。 若卖者进货量不足,则供不应求导致利润损失的期望为 现将式(5)作为进货量为Q的期望隐性成本(与文献[8]中的定义相同)。与前面式(2)不同,这里式(5)是将供不应求导致卖者的利润损失作为隐性成本。在期望隐性成本定义为式(5)的情况下,卖者进货量为Q的期望经济成本为 根据G1(Q)与G(Q)形式上的异同,在p>2c的情况下将式(3)推导过程中的p换成(p-c),可完全类似地得出G1(Q)最小化的进货量rm可由下面式(6)得出。 在期望隐性成本定义为式(5)情况下,卖者进货量为Q的期望经济利润为 由文献[8]知,WE(Q)最大化进货量rm的关系式(无需假定p>2c)可由下面式(7)得出。 综合式(6)和式(7)可知,在期望隐性成本定义为式(5)情况下,报童问题的期望经济成本最小化进货量关系式与期望经济利润最大化进货量关系式总体上(包括p>2c的情形)看是不同的,两者不可互换。事实上,由于期望经济成本G1(Q)表达式中不含模型外生变量u,G1(Q)最小化进货量关系式也是不会出现u的,故在期望隐性成本定义为式(5)情况下,不论是否满足p>2c,G1(Q)最小化进货量关系式都不会与式(7)一致,两者不可互换。 现在再进一步分析报童问题的期望经济成本最小化进货量关系式与期望经济利润最大化进货量关系式是否一致。由于报童问题的期望总收益表达式中含有单位残余收益,而这是一种“非正常”的销售收益,那么若不存在残余收益,即u=c,或v=0,情况会怎样? 第一,当u=c时,期望会计利润最大化进货量关系式(1)变为 因为期望显性成本cQ最小化进货量Q=r1,而式(8)中的rm不一定是r1。故当u=c时,一般而言期望显性成本最小化进货量与期望会计利润最大化进货量关系式仍然不同,两者不可互换。 第二,当u=c时,在期望隐性成本定义为式(2)情况下,期望经济利润最大化进货量关系式(4)变为 还是与期望经济成本最小化进货量关系式(3)不同,两者不可互换。 第三,当u=c时,在期望隐性成本定义为式(5)情况下,期望经济利润最大化进货量关系式(7)变为 仍与期望经济成本最小化进货量关系式(6)在p>2c情况下不同,两者不可互换。 第四,注意到式(3)与式(8)相同,这就是说在期望隐性成本定义为式(2)情况下当u=c时,期望经济成本最小化进货量关系式与期望会计利润最大化进货量关系式相同,两者可以互换。 此外,文献[7]中“模型七”推导出了期望赢利与期望损失的最优解可以互换,而实际上这里“期望赢利”是期望会计利润,而“期望损失”相当于在期望隐性成本定义为式(2)情况下的期望经济成本,故对该模型,期望经济成本最小化进货量关系式与期望会计利润最大化进货量关系式相同,两者可以互换。要注意的是与该文所描述的报童模型有所不同,文献[7]中“模型七”有存储费用,但没有供不应求时的单位亏损u,并且该模型的随机需求量是连续型的。 该文第一部分主要证明了特定的三次函数f(x)=ax3+bx2+cx+d(a>0,b<0)当自变量非负时严格单调增加的充分必要条件,即命题1,以及三次总成本函数几个通常应具备的重要特性,即命题2;得出了二次短期总成本函数所具备的必要特性,即命题3。这对检判一个三次总成本函数或二次短期总成本函数是否有误起到了便捷的作用。该文第二部分经过严格的论证得出结论:对于报童问题就一般意义而言,期望显性成本最小化进货量关系式与期望会计利润最大化进货量关系式不同,两者不可互换;在期望隐性成本定义为式(2)情况下,期望经济成本最小化进货量关系式与期望经济利润最大化进货量关系式不同,两者不可互换;在期望隐性成本定义为式(5)情况下,期望经济成本最小化进货量关系式与期望经济利润最大化进货量关系式不同,两者不可互换。当u=c时,在期望隐性成本定义为式(2)情况下,期望经济成本最小化进货量关系式与期望会计利润最大化进货量关系式相同,两者可以互换,即“期望隐性成本定义为式(2)并且u=c”是该文所述报童问题期望经济成本最小化进货量关系式与期望会计利润最大化进货量关系式相同,两者可以互换的一个充分条件。以上结论与传统经济学中关于成本和利润关系的结论不相悖,这对于报童问题的求解与经济学基本原理相融合具有正向价值。

2.2 期望经济成本最小化与期望经济利润最大化

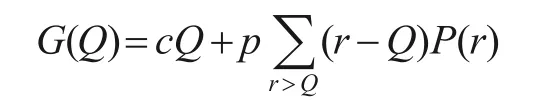








2.3 期望成本与期望利润解的互换性进一步讨论
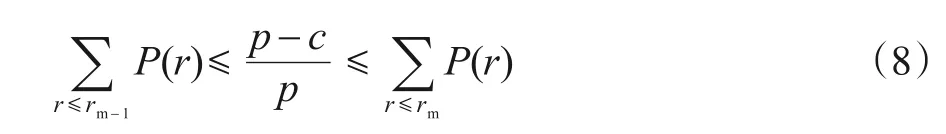


3 结论

