方形四立柱半潜式平台涡激运动特性数值模拟研究

王金涛，魏东泽，阙小玲，周江淮，张艺善

（浙江海洋大学 海洋工程装备学院，浙江 舟山 316100）

0 引言

在海洋工程领域一般将小直径结构物（如立管、海底管道）的流致振动定义为涡激振动（Vortex-Induced Vibrations, VIV），将大直径结构物（如Spar、张力腿和半潜式平台）的流致振动定义为涡激运动（Vortex-Induced Motions, VIM）。半潜式平台凭借其承载能力大、适应水深广、垂荡性能好和抗风浪能力强等优点成为了深海油气开发的主要装备之一，近年来，这种平台的VIM特性引起了学术界的广泛关注。由于半潜式平台结构特征的复杂性，导致其柱群效应较圆柱结构更为复杂，当前人们对于半潜式平台的涡激运动关键特性认仍然十分有限，诸多科学问题有待深入探索。

Rijken等[1]应用二维数值模拟的方法研究质量比和立柱形状对半潜式平台VIM响应的影响规律；Liu等[2]采用CFD方法对不同截面形式立柱组合的非对称平台进行了VIM研究，证明非对称平台的VIM仍是不可忽视的；Chen等[3]采用有限元分析方法，对四立柱深吃水半潜式平台在45°流向角下的VIM进行数值模拟，通过比较3种不同立柱倒角半径的半潜式平台，发现倒圆角的平台VIM横荡幅值更大，不足的是未考察其他流向角的情况；Kim[4]等采用延迟分离涡旋模拟-剪切应力输运（DDES-SST）方法，对一个八立柱半潜式平台VIM问题进行了数值模拟，并对结果进行了模型试验验证，发现在横荡、纵荡及艏摇响应方面拟合良好；Odijie[5]对立柱截面为正方形和长方形的半潜式平台进行了数值模拟，结果表明：发生VIM的约化速度范围均为2～12，与立柱截面形状无关，但横荡最大值出现在不同的约化速度下，且研究中未考虑艏摇的影响。Zhao等[6]采用雷诺平均法求解N-S方程，结合SST k-ω湍流模型对流向角为0°、15°、30°和45°，间距比等于3，约化速度为1～20的多圆柱VIM进行了数值模拟，发现流向角对VIM有很大影响。Lee等[7]采用三维数值模拟方法对深吃水半潜式平台的VIM响应特性进行研究，获得平台VIM响应的幅值特性、运动轨迹和受力特性，并分析了在锁定区前、锁定区和锁定区后的平台VIM响应和流场特征。田辰玲等[8]利用STAR-CCM＋软件，采用分离涡模拟（DES）方法对三立柱轻型半潜平台涡激运动特性进行了数值模拟，结果表明，0°流向角时艏摇运动达到最大幅值，在约化速度7.0≤Ur≤10.0区间发生锁定；陈元鑫等[9]对不同直径比的立柱组合在0°和180°两种流向角下的运动响应进行了二维数值模拟，发现拥有两个尺寸立柱直径的平台，流向角对平台横荡运动影响非常显著，但上述流向角代表性不足；李思明等[10]采用DES方法，分析得出倒角半径变化会影响上游立柱对下游立柱的干扰作用；谷家扬等[11]对低质量比弹性支撑方形四立柱涡激运动进行数值研究，结果发现，横向运动频率随折合速度的增加而增大，没有出现频率锁定现象，但研究中将平台简化为两自由度模型，未考虑艏摇运动；刘为民等[12]采用有限体积法对圆形四立柱涡激运动进行数值模拟，研究发现，圆形四立柱涡激运动流向和横向振幅随着折合速度的增大而先增大、后减小，并出现幅值跳跃现象，但研究中同样忽略了艏摇的影响。

半潜式平台的结构特征对VIM特性具有重要的影响，特别是立柱截面的形状、尺寸等，过去研究成果大多集中于圆柱结构平台，对方柱平台的研究相对较少，而方柱平台的柱群效应更为复杂，运动特性与立管等单圆柱结构或多圆柱结构有较大的区别，亟待深入研究。本文以方形四立柱半潜式平台为研究对象，采用CFD数值模拟的方法，对4种不同流向角下，约化速度Ur=1.85～15.43（对应流速区间为0.06～0.50 m/s）共16个工况的平台VIM响应特征进行较为全面的研究，并考虑了过去研究中往往忽略的艏摇运动，分析了三自由度运动之间的影响机理，重点考察了流向角对运动幅值和涡激力的影响。模拟过程中，将平台简化为质量-刚度-阻尼系统，采用四阶Runge-Kutta方程进行求解，并通过Fluent的用户自定义编程（UDF）实现流固耦合。

1 计算模型

本文中半潜式平台为方形四立柱结构，边长D为0.06 m，立柱中心距L为3D，即间距比L/D=3，计算域为58D⊆40D，流场入口和出口距立柱边缘距离为18D和36D，流场两侧距立柱边缘的距离为18D。流向角定义为来流方向与平台所成的角度，其中，θ为流向角，Oxy为固定坐标系，Ox′y′为随体坐标系。流场计算域和流向角定义如图1所示。

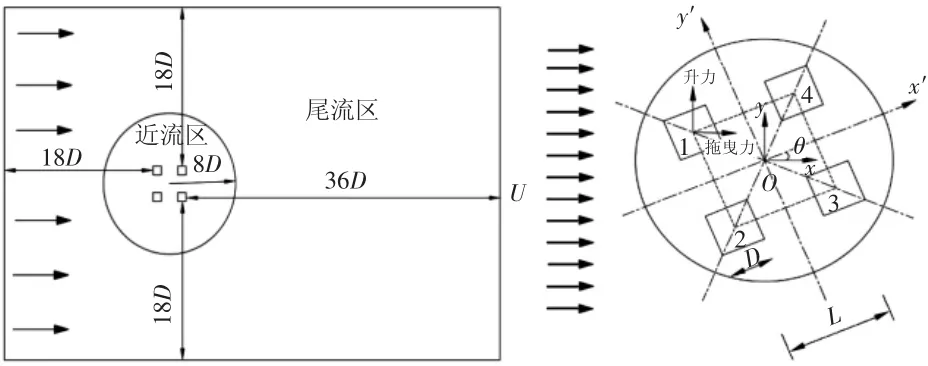
图1 流场计算域和流向角示意图

流场计算基于流体力学计算软件Fluent，采用SST kω湍流模型，流场的边界条件设置为：进口边界为速度入口，出口边界为压力出口，两侧边界为自由滑移边界，柱体壁面为无滑移壁面。采用动网格技术模拟流固耦合，在网格划分时，将平台周围8D直径范围内的流场划分为随体网格，与4个立柱一起做刚性运动，随体区域采用结构化网格，其他采用非结构化网格。划分网格时，首先划分0°流向角的网格模型（如图2），15°、30°和45°流向角的网格模型可以通过将随体网格分别旋转15°、30°和45°得到。

图2 0°流向角计算域网格及近场网格

2 计算结果与分析

2.1 不同流向角下平台三自由度运动响应幅值

0°流向角时，平台横荡、纵荡和艏摇响应幅值随约化速度Ur变化情况如图3（a）所示。从图中可知，三向运动响应幅值整体上随Ur的增大而增大。当Ur=1.85时，平台纵荡最大幅值仅为0.0039D，横荡幅值为0.017D，艏摇幅值仅为0.11°，此时平台尚未发生涡激运动。当Ur＞4.63时，平台纵荡、横荡和艏摇幅值随Ur的增大而增大，增速基本一致，均未发现锁定区后响应幅值下降的现象，因此通过运动幅值来界定锁定区范围难度较大。

从图3（b）～图3（d）中可以看出，当流向角为30°和45°时，平台运动特征有别于圆柱结构，三自由度响应幅值始终随Ur的增大而增大；当流向角为15°时，在Ur=3.70～6.48区间，发现了常见的频率锁定现象，即在锁定区内振幅快速提高，锁定区后振幅回落。但随着Ur的进一步增大，三自由度响应幅值随之增大，并在Ur＞11.11后超过锁定区的响应幅值，与“驰振”（Galloping）的特点较为相似，并从振动频率方面得到了验证（如图4）。

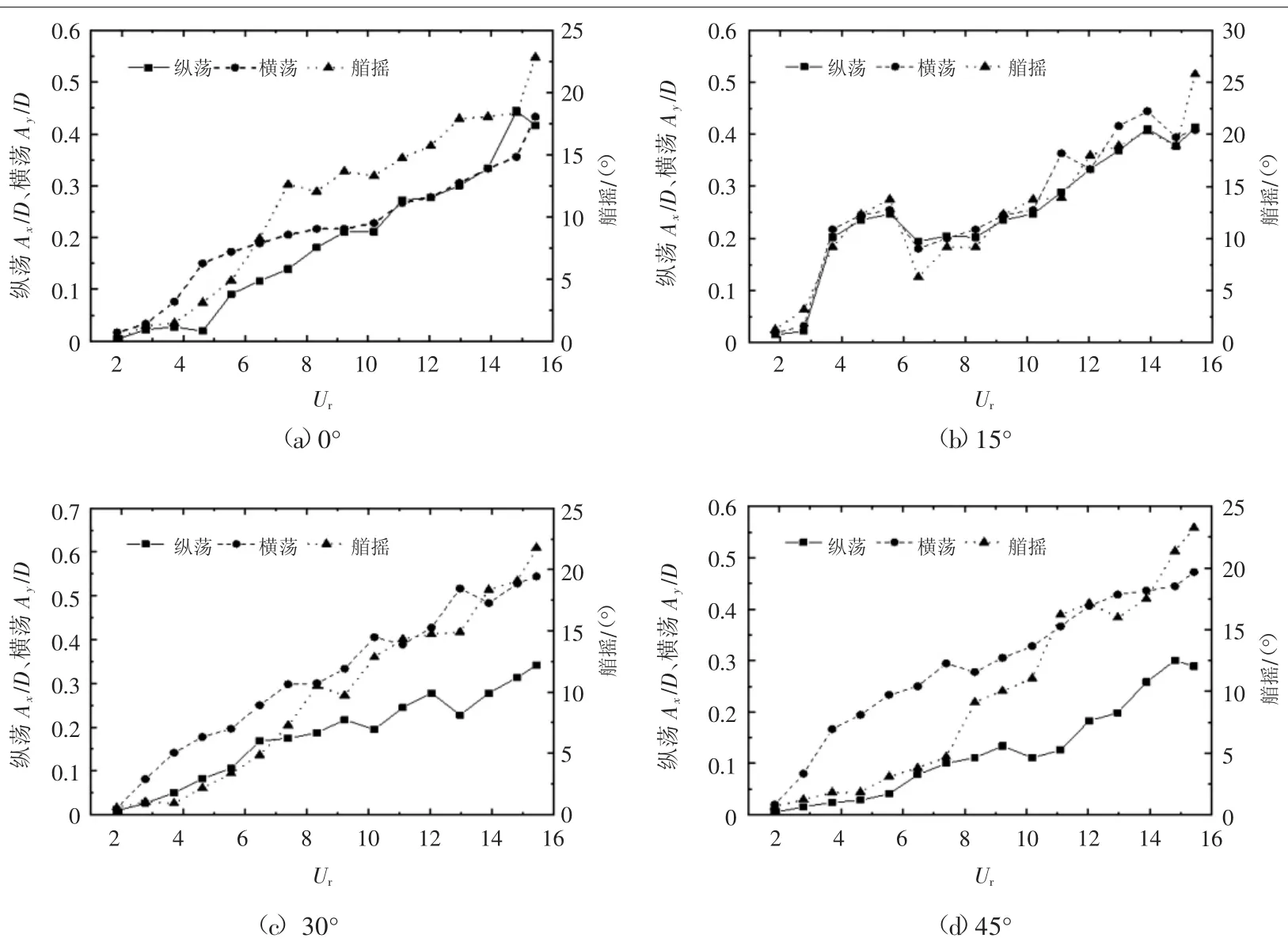
图3 不同流向角平台三自由度响应幅值随Ur的变化情况

图4 15°流向角下横荡功率谱密度（PSD）图

当流向角为0°和15°时，纵荡和横荡幅值随Ur增长的速率大致相同，幅值接近；当流向角为30°和45°时，横荡和纵荡的幅值差距较大，前者平均为后者的2倍左右，30°流向角时最大差距为5倍左右（Ur=4.63工况），45°流向角下最大差距为7倍左右（Ur=3.70工况），仍属于一个量级。此外，还发现不同流向角下，艏摇幅值均较大，最高可达25°以上，这主要是因为模型中设置了较小的弹簧刚度系数，证明艏摇不应被忽略。因此可以认为，平台的涡激运动以横荡为主导，但不应忽略纵荡和艏摇运动。

从图4可以发现，在Ur=3.7～6.48区间内，横荡具有明显的振动主频，且振动频率始终保持在固有频率附近，发生了频率锁定现象，但在大约化速度（Ur＞9）时，运动主频消失，振动频率小于1 Hz的运动能量占比较大，结合图3（b）横荡的运动幅值，可以发现在大约化速度时振动表现为低频、大振幅的特点，这与驰振的特点相符[13]。

2.2 不同流向角下平台三自由度涡激力系数

受篇幅所限，本文以Ur=4.63为例考察流向角对涡激力（以涡激力系数表示）的影响。由图5可见，不同流向角下平台受力情况差别较大：当流向角为0°时，升力Cl、拖曳力Cd和艏摇力矩Cm系数分别为6.29、1.40和0.49，对应频率主峰值为0.55 Hz、1.10 Hz 和0.55 Hz，涡激力系数频率主峰值之比为1:2:1；当流向角为15°时，Cl、Cd和Cm分 别 为5.90、5.22和0.21，涡激力/力矩系数频率主峰值（均为0.40 Hz）之比为1:1:1，升力和拖曳力系数出现了约为0.6 Hz的次峰频率，与主峰频率之比为1:1.5；当流向角为30°时，Cl、Cd和Cm分 别 为7.56、3.47 和0.32，涡激力/力矩系数主峰频率（均为0.51 Hz）之比也为1:1:1，拖曳力次峰频率与升力次峰频率成2倍关系；当流向角为45°时，Cl、Cd和Cm分别为6.62、1.44和0.34，涡激力/力矩系数主峰频率之比为1:2:1。

图5 不同流向角下Ur=4.63时涡激力系数时程曲线及频谱图

总体来看，流向角会对平台受力产生很大影响。当约化速度为4.63时，4个流向角下，θ＝30°时平台升力系数最大，约为最小工况（θ＝0°）的1.28倍，θ＝15°时平台拖曳力系数最大，约为最小工况（θ＝0°）的3.73倍，而艏摇力矩则相差为2.33倍（θ＝15°时最大，θ＝0°时最小）。当流向角为0°和45°时，Cl、Cd和Cm频率主峰值之比为1:2:1，而当流向角为15°和30°时，Cl、Cd和Cm频率主峰值之比为1:1:1，涡激力/力矩频率具有较强的规律性，表明三向振动之间存在强耦合性。不同流向角下，升力系数和艏摇力矩系数始终保持1:1关系，可以推断艏摇受横荡控制，这一结论与前人的研究成果一致[12]。此外，在多个流向角下发现了较为明显的次峰频率，次峰频率的出现会导致涡激力系数曲线的简谐性减弱，随机性增强。

3 结论

基于雷诺平均N-S方程和SST k-ω湍流模型，建立了方形四立柱半潜式平台数值模型，从横荡、纵荡和艏摇三自由度响应幅值、涡激力系数、质心运动轨迹等方面出发，对半潜式平台涡激运动特性进行了分析，得到结论如下：

1）方形四立柱平台VIM仍以横向运动为主，但不应忽略顺流向运动和艏摇运动。

2）方形四立柱平台与单圆柱或多圆柱结构的VIM有明显差异，在大约化速度时运动幅值未发生明显下降，而是随着Ur的增大而增大，表现出一种涡激运动和驰振相结合的特征，这可能与流向角以及结构特征有关。

3）流向角会对平台受力有较大影响，当平台处于来流方向对称的方位时（θ为0°、45°），升力系数与拖曳力系数主频率比为1:2，而当平台来流方向上不具有对称性时（θ为15°、30°），升力系数与拖曳力系数主频率比为1:1，无论何种流向角，升力系数和艏摇力矩系数主频率比始终保持为1:1，可以推断艏摇是受横荡控制的，进一步说明艏摇也是由涡旋发放引起的。