某流域年均含沙量的非线性回归分析

于世龙，杨奉广

（四川大学水利水电学院，四川 成都 610002）

0 引言

我国河流众多，自然资源尤其丰富，但随着人类活动范围的不断扩大，很多流域下垫面条件被改变，水土流失现象十分严峻，给国家的可持续性发展以及生态环境带来较大的危害。黄河作为世界上含沙量最多的河流，多年平均年输沙量达16亿吨之多[1-3]，黄河下游大量的泥沙淤积。如何定性定量的分析含沙量对于泥沙治理、河道通航和防洪具有重大意义，有关泥沙输移机理的研究，国内外许多学者都取得了较大的进展，陈浩[4]针对产沙因素降雨特征和地貌特征进行了对产沙影响的定性分析；张醒[5]通过来沙系数公式推求水系间泥沙；于东生等[6]根据ADCP资料，建立BP神经网络模型对长江口的泥沙含量进行了研究；彭清娥等[7]针对采伐面积、采伐量、降雨量、和年均径流量，采用神经网络的方法建立了流域年均含沙量模型；杨佳璐等[8]在神经网络的基础上，引入人工蜂群的算法，建立了含沙量预测模型。

但是目前已存所建立的模型，还存在着相对误差比较大、不够准确等问题，为了减小得出模型的相对误差，本文采取非线性回归的方法对流域年均含沙量进行预测，从而得出了一个更为精确的模型，以期该模型以后可以为定量开展河流年均含沙量预测研究提供参考。

1 材料与方法

本文数据选自文献[7]，里面有某流域1961—1978年期间有关年均含沙量的18组数据。本文首先采用多元线性回归方法，对数据进行拟合，建立回归模型，并进行回归模型评估及显著性分析，发现多元线性回归得出的模型偏差较大。因此只能考虑非线性回归方程进行拟合，考虑了10种可线性化回归的曲线回归方程，最终确定可化为线性回归的曲线回归模型比较符合年均含沙量模型，而且精度较高。以下就是具体方法：

本文选取了文献[7]中某一小流域的采伐面积（A）、采伐量（V）、降雨量（i）、流域年均流量（Q）、粒径（d）这五个主要因素对流域年均含沙量（θ）进行建模预测，因为这些变量都是量纲的，为使结果更为直观，对其进行量纲归一化处理，然后5个变量就变为11个变量了，分别令

即考虑11个自变量Xi对因变量Y进行建模预测即可。

1.1 多元回归

建立经验关系通常有两种方法，即加法线性回归、乘法线性回归，公式如下：

式中，Y是因变量，Xi是自变量；θ为流域年均含沙量（kg/m3）；A为流域采伐面积（m2）；V为流域采伐量（m3）；i为降雨量（mm）；Q为流域年均流量（m3/s）。注意，方程（2）通过对方程两边做对数变换，可以很容易地转化为一个加法函数。对于任何已知的Xi值，式(1)或式(2)可以写成：

1.2 回归模型评估

必须要通过评估得出的的多元回归模型，才能确定回归分析的结果。公式（1），（2），（3）是多元回归的其中三种形式。

拟合优度是与回归公式和每个观测数据之间的接近程度相关的指标，其通常能总结出观测值与通过多元回归方程获得的模型的预测值之间的差异。在回归分析中，模型识别涉及到控制变量的选择和函数形式，这些控制变量与流域年均含沙量密切相关。拟合优度的一个指标与残差有关，定义为ej=yj-yj，yj和yj是第j个因变量的观测值和预测值。基于最小二乘法，通过最小化残差平方和得到回归系数的估计为：

决定系数R2为：

其中SSE成为残差平方和；SST称为总离差平方和；yadv代表因变量yi的平均值。

R2的值代表了考虑的回归模型所解释的Y的可变性[9]。换句话说，R2更大的模型表明对数据集的拟合良好程度较高。但是，当给模型增加自变量时，复决定系数也随之逐步增大，因为残差自由度等于样本个数与参数个数之差。自由度小意味着估计和预测的可靠性低。这表明当一个回归方程设计的自变量很多时，回归模型的拟合从表面上看是良好的，而区间预测和区间估计的精确度却变得很低，以至失去实际意义。这里回归模型的拟合良好掺杂了一些虚假成分，为了克服样本决定系数的这一缺点，我们设法对R2进行适当的修正，使得只有加入有意义的变量时，经过修正的样本决定系数才会增加，这就是所谓的自由度调整复决定系数。

设为调整的复决定系数，n为样本量，p为自变量的个数，则

式中，k为使用的控制变量个数。如果额外的控制变量不能十分有效地改进对数据变化的解释，则用k变量的改进的系数比用k-1改进的系数小。因此，通过比较值，可以选择一个简化的预测模型，其只考虑了最为重要的几个控制变量。

在进行回归参数的估计前，我们用多元线性回归方程去拟合随机变量y与变量x1，x2，…，xp的关系，只是根据一些定性分析所做的一种假设。因此，在求出线性回归方程后，还需对回归方程进行显著性检验[10]。通常用的是两种统计检验方法，一种是回归方程显著性检验的F检验；另一种是回归系数显著性的t检验。

（1）F检验

通常用于检验回归方程的显著性，以下是F检验的常用步骤：

a提出假设。

bF统计量计算。

对H0的统计量检验称为F检验，表达式如下：

其中SSE成为残差平方和，SSE=SST-SSR，根据以上表达式，F统计值明显满足F分布，除此之外F统计值越大，多元线性回归模型越精确。

（2）t检验

在多元线性回归中，回归方程显著并不意味着每个自变量对y的影响都显著，我们总想从回归方程中剔除那些次要的，可有可无的变量，重新建立更为简单的回归方程，所以需要对每个自变量进行显著性检验。

t检验，通常用于检验每个自变量对于因变量是否有显著性影响。t检验要对每个βi（i=1，2，…，k）进行单独检验。t检验的常规步骤跟F检验很近似。

a提出假设。

bt统计量计算。对H0的统计量检验称为t检验，表达式如下：

其中，sβ^i为估计值的标准差，ti代表第i个自变量的t统计值。

c统计决策。

（3）预测多元回归等式

按照上述原理，对这一组数据进行多元线性回归拟合，并进行回归模型评估及显著性，很小，而且p值远大于0.05，可知这些数据的多元线性回归模型偏差较大，可知这些数据之间不成线性关系。然后，又选取的10种可线性化的曲线（双曲函数、线性函数、对数函数、逆函数、二次曲线、三次曲线等）回归模型进行拟合，经检验检验这些数据的双曲函数模型拟合度较高，因此选用双曲函数模型：

因此，该模型转换成多元线性回归模型了，这时，只需要确定a，即能进行多元线性回归分析了。

选取a的准则：假定一个a，用11个变量xi对y′进行回归分析，求出决定系数R2，绘制出a与R2关系图，寻找出R2的最大值，所对应的a值，即为最终所选。

首先a的取值范围较大，寻找R2较大的区间，通过关系图得出一个较小的范围，如下图所示。

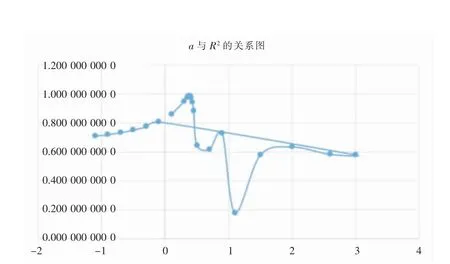
图1 a与R2的关系图

图2 缩小范围后a与R2的关系图

由左图可知，a值范围应该在0-1之间，按照同样的原理，找出随着a取值变化，R2值最大的附近区域，得出右图关系图。

由上图可知，a值取0.38附近，决定系数较高，但是此时的数据当中y′有一个极大的异常值，实际中按照此a值，进行回归分析将会造成回归分析的F检验、t检验完全失效，且相对误差极大。通过在其附近取值，进行回归模型评估、显著性分析及相对误差分析，最终确定a为0.3，此时得出的模型较为准确。

2 结果与讨论

2.1 回归分析

在一个实际问题的回归模型中，自由度调整复决定系数越大，所对应的回归方程越好。从拟合有度的角度追求最优，则所有回归子集中最大者对应的回归方程就是最优方程。

接下来对数据做所有子集（除了全模型）回归分析，由上文可知，一共有11个自变量，所以一共有2^11-2集的模型回归结果，并以调整的复决定系数作为标准选出最优子集，对于所选的自变量而言，回归分析的调整的复决定系数最大的模型即为最佳的包含对应自变量的模型，根据函数编程，先展示一个最佳的单解释变量模型，然后展示一个最佳的含有两个解释变量的模型，依次类推，直至展示一个最佳的包含10个解释变量的模型，对每个模型进行回归分析，结果如表1。

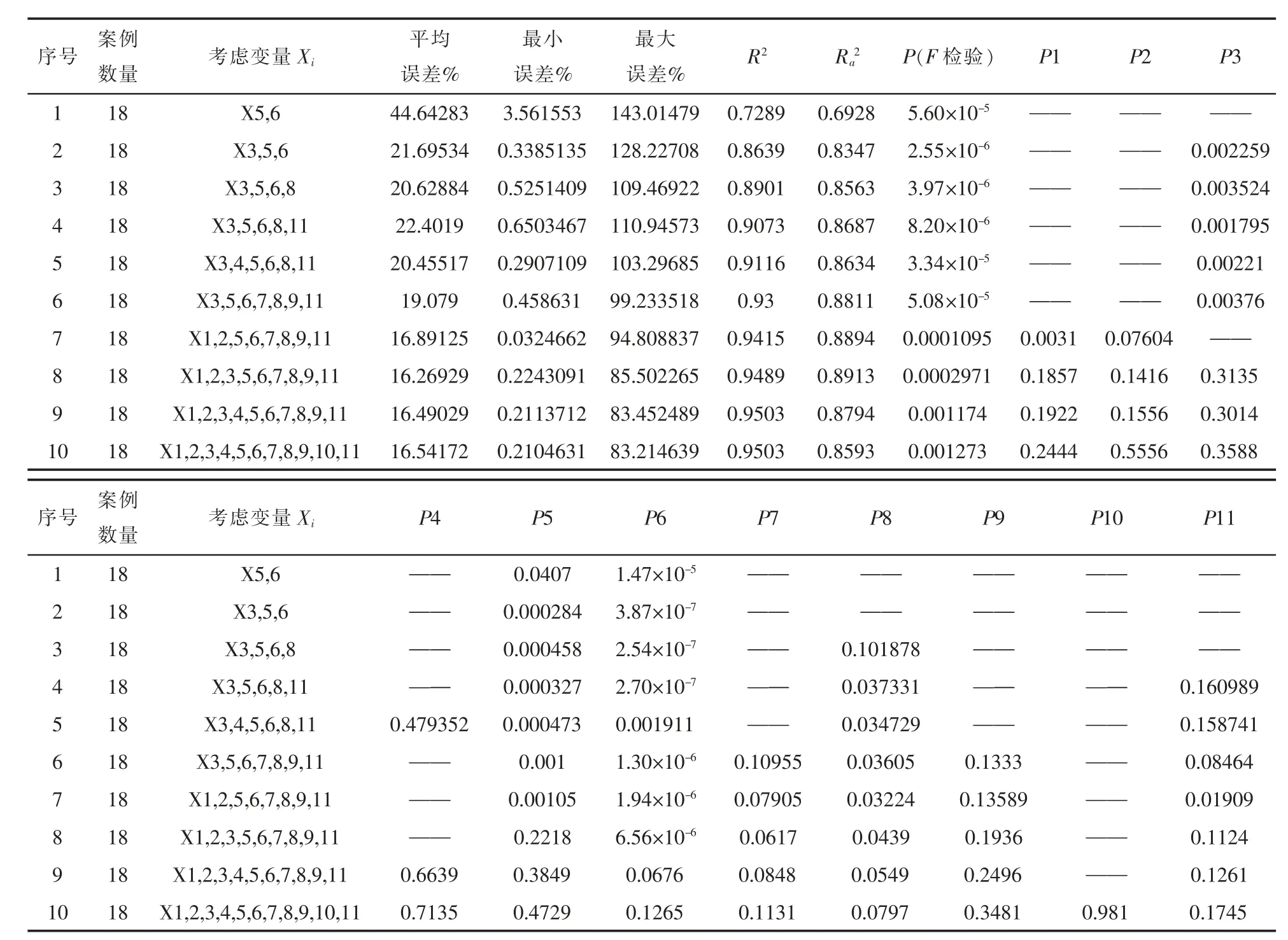
表1回归模型的评估结果

由表1可知以X3，X5，X6，X7，X8，X9，X11作为自变量的模型为最佳的含有7个解释变量的模型，使用初始的年均含沙量的自变量，年均含沙量自变量的预测值方程为：

由以上结果可知以X1，X2，X5，X6，X7，X8，X9，X11作为自变量的模型为最佳的含有8个解释变量的模型，使用初始的年均含沙量的自变量，年均含沙量自变量的预测值方程为：

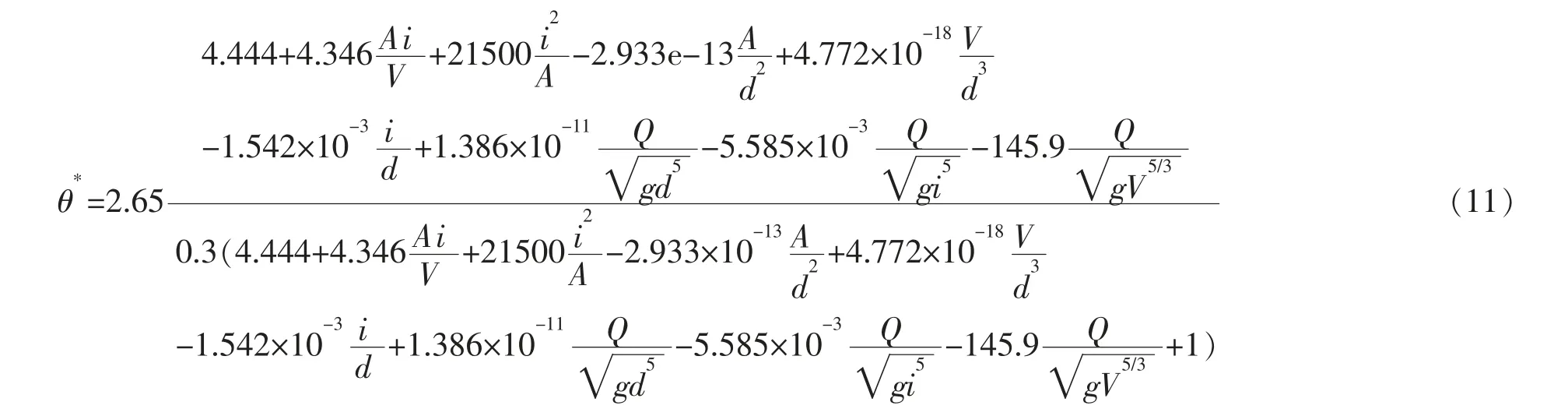
由以上结果可知以X1，X2，X3，X5，X6，X7，X8，X9，X11作为自变量的模型为最佳的含有9个解释变量的模型，使用初始的年均含沙量的自变量，年均含沙量自变量的预测值方程为：

由以上结果可知以X1，X2，X3，X4，X5，X6，X7，X8，X9，X11作为自变量的模型为最佳的含有10个解释变量的模型，使用初始的年均含沙量的自变量，相应等式写成：

对11个自变量xi以及因变量y′进行回归分析，使用初始的年均含沙量的自变量，年均流量的预测公式为：

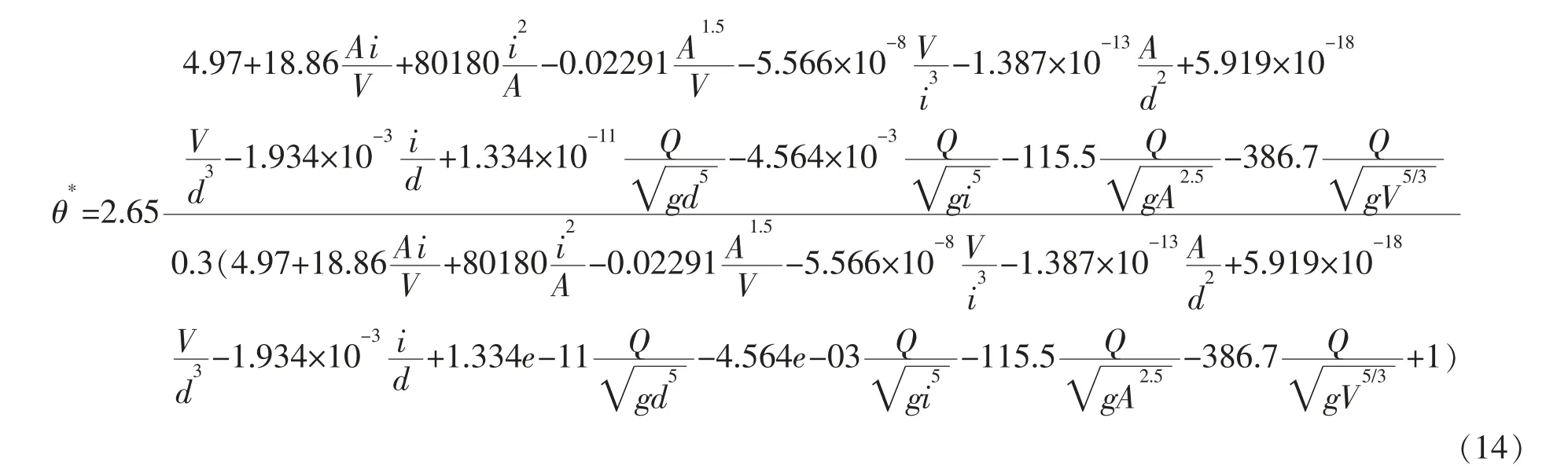
实际回归分析过程中发现，最大误差都出现在第12组数据中，因而可以去掉12组，再进行回归分析，可以得出更为精确的预测值，分析如下。

对新的数据进行同样的分析，结果如表2。

表2去掉12组后回归模型的评估结果

由表2可知以X1，X5，X6，X7，X8，X9，X10，X11作为自变量的模型为最佳的含有8个解释变量的模型，使用初始的年均含沙量的自变量，年均含沙量自变量的预测值方程为：

其中复决定系数为0.9703，调整的复决定系数为0.9406，且P值为2.531×10-5远小于0.05，模型总体较为显著，而且各个系数都通过了显著性检验。而且在所有的模型中，它的误差也相对较小，由此，其模型为最理想的模型。

由以上结果可知以X1，X3，X5，X6，X7，X8，X9，X10，X11作为自变量的模型为最佳的含有9个解释变量的模型，使用初始的年均含沙量的自变量，年均含沙量自变量的预测值方程为：

由以上结果可知以X1，X2，X3，X5，X6，X7，X8，X9，X10，X11作为自变量的模型为最佳的含有10个解释变量的模型，使用初始的年均含沙量的自变量，相应等式写成：

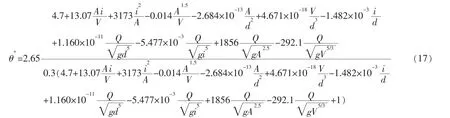
回归分析的一些关键性参数列在了表1和表2中，这些总体回归模型的决定系数R2绝大多数都在0.87以上，表明实测值和预测值只存在轻微差别，证实了提出的回归等式的有效性。

2.2 显著性分析

显著性检验用于根据预定的显著性水平α确定拒绝零假设的输出值阈值。如果P值和Pi值小于默认值0.05，则因变量和各个自变量之间的多重线性相关性具有统计显著性。本文显著性水平取0.064。

对于所有的预测方程，显著性检验结果列在了表1和表2中，表中大多数P值的数量级均小于10-5，而式9，10，20的数量级为10-3。以式20为例，在假设H0正确的前提下，较大的P值表明各自变量从总体上对因变量的影响尤为显著的可能性越小，但是其值仍然小于显著性水平，表明所有的自变量从整体上仍对因变量具有统计显著性所以所有方程的自变量从整体上对因变量具有统计显著性。

然而每个多元回归等式的Pi值并不相等，大多数的Pi值都大于显著性水平α，以式8为例，在假设H0正确的前提下，较大的Pi值表明，从所提供的数据库中发现自变量xi与因变量之间线性关系的概率大于大多数因变量和其他回归系数测试中的任何自变量之间的线性关系的概率。但是很多自变量的显著检验不能通过表明其对因变量的影响并不显著，这种情况需要将该变量舍去，重新进行多元回归分析，在看结果。

图3 各个模型的比较图

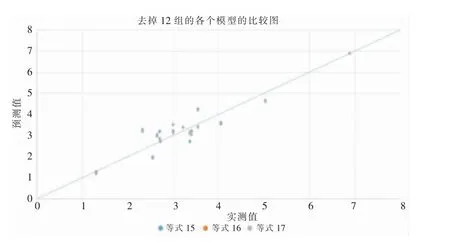
图4 去掉12组后的各个模型比较图

通过表一表二可以看出式17的效果比较好，它的P值为0.00002531远小于显著性水平α，表明各个自变量从总体上对因变量的影响显著。而且t检验的最大的Pi值为0.0635，小于预定的显著性水平α，其他的Pi分别为0.000761、0.000126、5.29×10-7、0.054055、0.023671、0.034193、0.005903，均是小于显著性水平，表明各个自变量对因变量的影响都显著。该模型完美通过显著性检验，而且决定系数R2为0.9703、调整的决定系数为Ra2为0.9406，系数已经非常高了，而且在所有等式里面也是基本上最高的了，所以式17为最佳的预测模型。

2.3 对比分析

为了更为直观的看看各个模型的拟合效果，以实测值为横坐标，预测值为纵坐标绘图，分别绘制原有数据的各个模型比较图以及去掉12组的各个模型比较图。

比较分析两组图，可以得出以下几点：

（1）去掉12组的各个模型拟合较高，较为理想。

（2）当年均流量2.3<θ<5时，数据较为集中，且都贴近坐标轴45度线，表明这个区域的数据拟合度尤为高。

（3）对比两组图可以发现，等式17-20的拟合情况相对较好，然后可以再结合一些指标，选出最优的拟合模型，作为本次研究的结果。

3 结论

本文通过引入复杂非线性回归方法对流域年均含沙量进行预测，得出以下结论：

（1）流域年均含沙量的复杂非线性回归模型是流域产沙预测的一种非常有效的方法。

（2）该方法相对于目前现存的一些方法具有相对误差更小的优点，能为日后定量开展河流含沙量预测研究提供参考价值。