光伏水泵系统PWM输出滤波方法及影响分析

杨健，苏建徽, 马志保，瞿晓丽

(合肥工业大学 光伏系统教育部工程研究中心，合肥 230009)

0 引 言

太阳能光伏水泵系统非常适用于无电地区的扬水工程，随着光伏水泵系统国内外广泛应用，且由于其常处于偏远交通不便地区，可靠性和寿命问题是需要关注和研究的，工程应用中最常发生的故障是水泵电机损坏现象，统计发现光伏水泵电机的故障率常高于电网供电的水泵系统，采用常用的在逆变器输出侧单独串电感方式效果不是十分明显。因此，需要进一步研究分析原因。

关于电网供电的变频装置对电机系统故障及寿命影响已有相关研究。文献[1]对变频供电共模电压的形成机理进行了分析，推导出轴电压，轴电流形成的原因，提到在轴电流的侵蚀下，电机轴承的使用寿命会变为不使用变频供电系统的七分之一。文献[2]表明PWM逆变器产生的高频共模电压通过电机内部的耦合电容产生高频共模电流，进而产生电磁干扰(EMI)问题，对系统内其他电气设备的正常工作造成影响。光伏水泵系统中，由于阵列电压高于电网峰值电压，水泵电机侧的共模电压幅值就会高于电网供电的变频系统。因此对光伏水泵系统共模电压、电流抑制的研究具有重要的意义。

文献[3]对共模电压与电流的产生机理进行了详细的分析，提出共模电压脉冲的变化率是影响共模电流的主要因素，脉冲的变化率越快，共模电流越大，但是并未提出抑制共模电压与电流的方法。文献[4]提出一种将RLC滤波器的公共端与直流母线的中点连接在一起的滤波器，用来抑制共模电压，但是并未对其抑制的原理进行分析，也没有给出具体的滤波器参数设计方法。

文章针对逆变器所引起的共模电压与共模电流问题，建立了共模等效模型，对共模电压与电流的产生机理进行了分析。对于共模电压与电流的抑制，采用LC滤波器与直流母线负端相连的方式，并对此方法的抑制原理进行了详细的分析；通过对增加此滤波器的电机控制系统所受影响的分析；优化了此滤波器的参数选取方法。最后对以上研究进行了实验，结果表明提出方法的正确及有效性。

1 共模电压与电流产生机理分析

光伏水泵系统一般采用两电平三相全桥逆变驱动系统。其结构如图1所示，电机与光伏板都有效接地。其中：P为光伏母线正极端点；N为光伏母线的负极端点；O为三相定子绕组中性点；Ceq为电机内部等效耦合电容(由Cwf定子绕组与机壳之间的耦合电容Cwf、定子绕组与转子之间的耦合电容Cwr、转子与机壳之间的耦合电容Crf、轴承电容Cb组成[5])；R0为电机每相等效电阻；L0为电机每相等效电感；ucm为电机等效耦合电容电压；经过等效耦合电容Ceq流向大地的电流icm为共模电流。

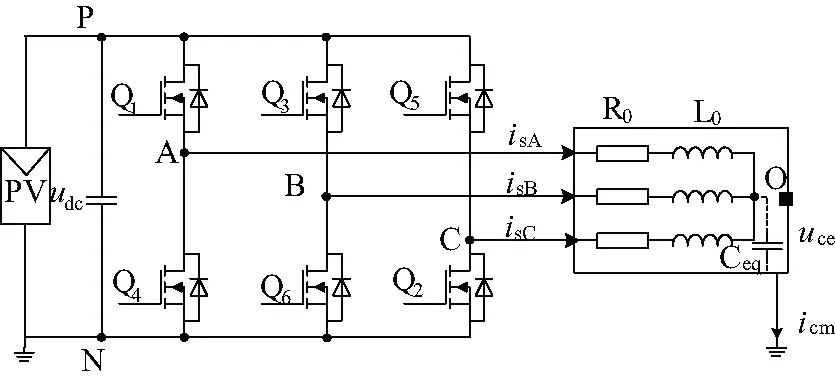
图1 光伏水泵系统结构图

图1中，uAN，uBN，uCN分别为A点，B点，C点相对于大地N的电势差；光伏水泵系统的共模电压ucm定义为三者的平均值[6]：

(1)

由基尔霍夫电压定律可知：

(2)

式中uIN表示I相桥臂输出的电压；isI表示I相桥臂输出电流。

结合式(1)与式(2)可得：

(3)

由于电机等效耦合电容通过电机机壳与大地相连[7]，进而与主电路之间形成回路，在共模电压的作用下产生共模电流icm。

(4)

将式(4)带入式(3)可得：

(5)

由式(5)可以得到，光伏逆变器的共模等效模型，如图2所示。

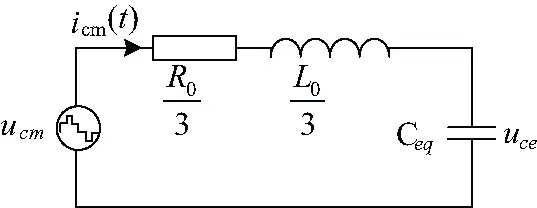
图2 光伏逆变器的共模等效模型

由两电平三相全桥逆变驱动方法并结合图1可知，IGBT每动作一次，逆变器输出的共模电压就改变udc/3，类似于输入信号是阶跃信号，共模电压与共模电流是阶跃响应，则该电路阶跃响应的通解为：

(6)

式中ωn为无阻尼自然振荡角频率；ξ为阻尼比；Z0为特征阻抗；φ为ueq的相角。结合图2中的参数可以得到：

(7)

由式(6)可以看出,如果共模电压ucm的上升或下降时间大于振荡周期的一半时，共模电流将极大的减小。

2 PWM输出滤波方法分析

2.1 LC滤波器对共模电流的抑制

PWM输出滤波方法采用LC滤波器，其拓扑电路如图3所示[8-10]。

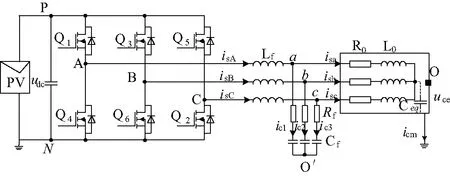
图3 LC输出滤波电路拓扑图

由基尔霍夫电压定律可知：

(8)

式中uIN为I相桥臂输出的电压；isI为I相输出电流；isi为电机侧输入电流。

通过图3可以看出O′悬空与主回路没有直接的电气连接，故滤波电容Cf不会流过零序电流，可得共模电流icm的表达式：

(9)

由式(8)、式(9)可得：

(10)

结合图2与式(10)可得采用LC滤波器时光伏逆变器的共模等效模型，如图4所示。

图4 采用LC滤波器时的共模等效模型

从图4中可以看出，相较于图2所示的光伏逆变器的共模等效模型，采用LC滤波器的共模等效模型中，只增加了滤波电感，相当于增大了图2中的电感L0，随着电感L0增大，LC滤波器的无阻尼自然振荡角频率ωn降低，可以有效地滤除共模电压中的高频成分。但是随着谐振频率ωn降低，系统在载波频率处发生谐振的可能性增大，导致共模电压在载波频率处的电压幅值增大，对系统产生更严重的危害。

2.2 改进型LC滤波器对共模电流的抑制

改进型LC滤波器是将LC滤波器的星型连接点与光伏母线的负端相连的滤波器，其拓扑结构如图5所示。

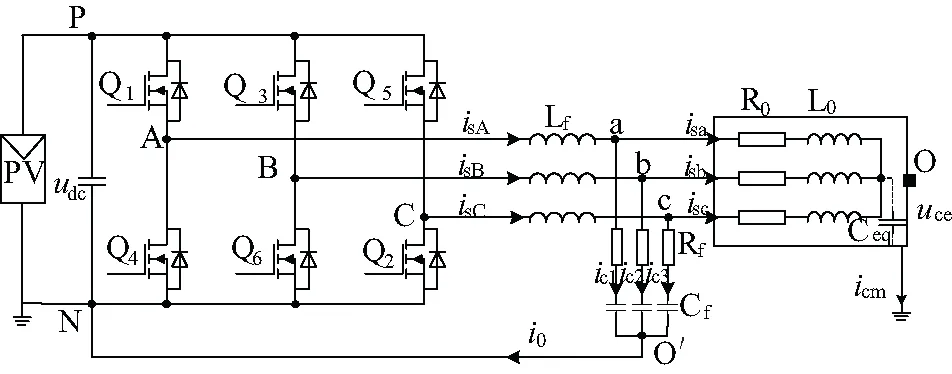
图5 改进型LC输出滤波电路拓扑图

根据基尔霍夫电压定律和基尔霍夫电流定律，可得：

(11)

式中ic1、ic2、ic3为滤波电容电流；定义三相滤波电容电流之和为i0。考虑电机是三相对称系统，由式(11)可得：

(12)

联合图2和式(12)可得采用改进型LC滤波器时光伏逆变器的共模等效模型，如图6所示。

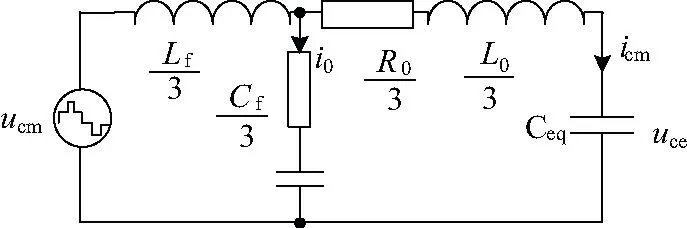
图6 采用改进型LC滤波器时的共模等效模型

由图6可以看出，LC滤波器与电机中的等效电感构成LCL滤波器。由图6可得等效耦合电容电压uce对共模电压ucm的传递函数为:

(13)

考虑到电机等效耦合电容Ceq较小，一般为钠法级的电容，所以可得：

(14)

通过式(14)可以将式(13)简化为：

(15)

由式(15)可以看出，H(s)简化为一个二阶系统。可得出谐振振频率满足：

(16)

式中ωres为H(s)的谐振频率；ωresl为LCL滤波器谐振频率；λ=L0/Lf为电感比；η=Ceq/Cf为共模电容比；τ为谐振频率比。根据式(16)，可得谐振频率比τ与电感比λ和共模电容比η之间的关系曲线，如图7所示。

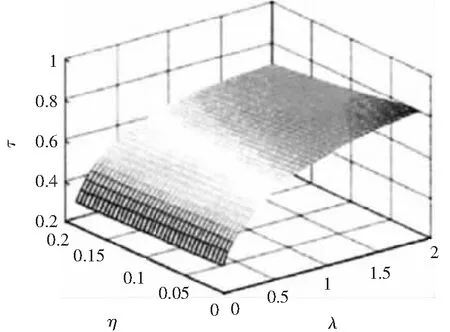
图7 谐振频率比与电感比和共模电容比的关系曲线

从图7中可以看出，无论电感比λ和共模电容比η如何变化，谐振频率比τ总是小于1，所以只要优化设计LC滤波器的参数Lf，Cf就可以在滤除电机耦合电容电压的高频分量的同时，又可以避免在主要谐波附近发生谐振。

3 输出滤波器对光伏水泵控制系统的影响

3.1 输出滤波器对V/F控制系统的影响分析

感应电机的V/F控制中，由电机理论可知，电机的定子感应电动势为[11]：

e1=4.44f1N1KN1Φm

(17)

则有Φm=e1/(4.44f1N1KN1)即Φm∝(e1/f1)，在电机的V/F控制系统中通常使用逆变电压U1替代感应电动势e1。通过改变逆变器输出电压频率的同时改变输出电压，使输出电压与输出电压频率比保持为一个恒定的常数，以维护电机磁通基本恒定的调速方式。

电机的电磁转矩方程为[11]：

(18)

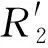
逆变输出接LC滤波器后，滤波电感与滤波电容在高频脉冲的作用下产生阻抗，此时LC滤波器相当于一个分压电路，导致电机侧的定子电压降低。此时依然以逆变输出电压U1代替感应电动势作为控制电压，显然会存在一定的误差。由式(18)可知，在电源频率、电动机结构与转速一定时，电动机的定子电压降低将引起电磁转矩的大幅度降低。LC滤波器的单相等效拓扑结构见图8。

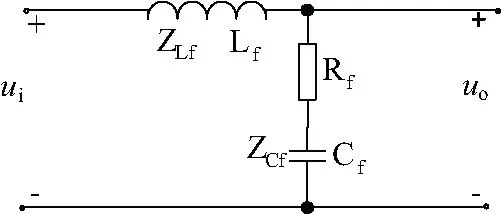
图8 加LC滤波器的单相等效拓扑结构

由基尔霍夫电压定律可知，其输出电压的关系如下：

(19)

式中ZCf为滤波电容的阻抗；ZLf为滤波电感的阻抗；ω为载波频率。

由于在工程应用中允许存在20%的定子压降，选取LC滤波器的参数时应当满足以下条件：

(20)

3.2 输出滤波器对矢量控制系统的影响分析

光伏水泵矢量控制系统实际上是根据感应电机的动态数学模型，利用一系列的坐标变换把定子电流矢量分解为励磁分量与转矩分量，对电机的转矩分量和励磁分量分别进行控制，从而达到控制异步电机转矩的目的[12]。

PWM逆变器外接LC滤波器增加了电容电流支路使电机定子的电流相位与幅值发生了改变。传统的光伏水泵控制系统电流采样电路设置在逆变器侧，水泵电机电流不能直接控制，导致在光伏水泵矢量控制系统中无法准确地进行水泵电机的磁场定向以及励磁电流与转矩电流的控制。

逆变器输出侧电流经过坐标变换至dq同步旋转坐标系下的电流表达式为[13]：

(21)

电机侧定子电流经过坐标变换至dq同步旋转坐标系下的电流表达式为：

(22)

通过式(21)与式(22)可以看出，由于滞后相位角度φ的存在，使得实际反馈d、q轴电流幅值发生变化并且存在耦合的逆变器输出d、q轴电流分量。而滞后相位角度φ的大小与所选取滤波电容的大小有关，通过逆变输出接LC滤波器的感应电机单相等效拓扑结构,可以计算出滤波电容Cf与滞后相位角度φ的关系。拓扑电路图如图9所示。

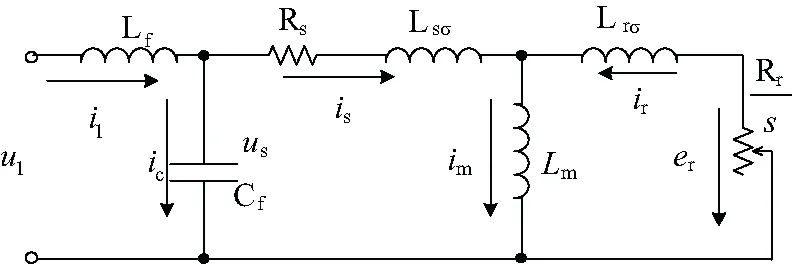
图9 加LC滤波器的感应电机单相等效拓扑结构

由基尔霍夫电流定律可得：

(23)

由式(23)可以得到定子电流相位滞后角φ与滤波电容Cf之间的关系曲线如图10所示。随着滤波电容的增大，定子电流相位滞后角度也变大。从图10中可以看出当滤波电容小于4 μF时，滞后相位角度φ几乎为0，若选取此时的滤波参数，对电机的矢量控制的影响相对较小。

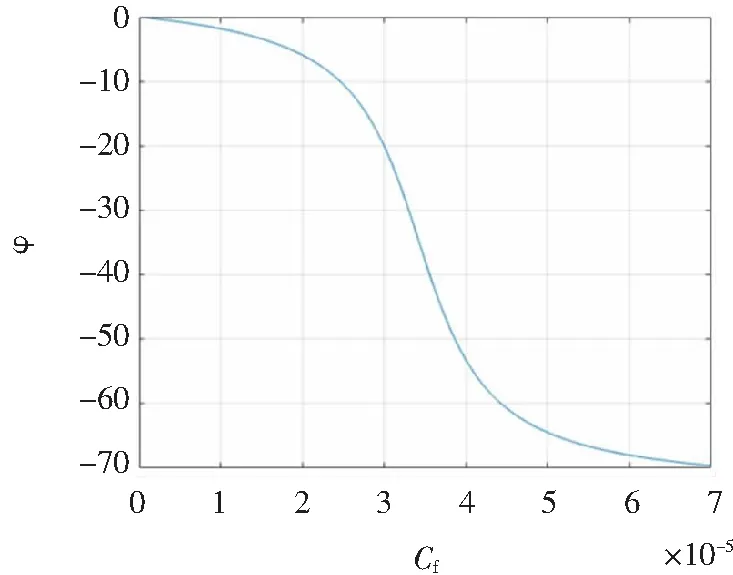
图10 滤波电容与相位滞后角度得关系

4 参数设计

由图6可得，电机侧的共模电压相对于逆变侧共模电压的传递函数为：

(24)

式中ωns=1/(sqr(LfCf))为滤波器的自然振荡频率；ξs=(Rf/2)(sqr(Cf/Lf))为滤波器的阻尼系数。

由式(6)可得，可以通过延长脉冲上升时间，抑制共模电流。为实现此目标，理论要求LC二阶系统的单位阶跃响应无超调，即阻尼系数ξs必须不小于1[14]。

根据ξs与单位阶跃响应上升时间tr之间的关系，可推导出tr与ωns的关系：tr≤0.78/ωns可知：

(25)

由式(25)与ξs推出Lf，Cf需满足条件：

(26)

同时Lf和Cf的选取还需满足式(20)的要求。式(26)表明：Lf和Cf的最小值不仅与Rf有关，而且与tr有关。通常tr取值为电机无阻尼自然振荡角频率ωn的一半以上，而Rf通常为特征阻抗值Z0。

5 实验结果

为了验证此参数选取方法的有效性，搭建了3 kW光伏水泵系统实验平台。水泵电机的参数为：un=220 V，额定功率Pn=3 kW，额定转速nN=1 420 r/min，极对数P=2；逆变器载波频率为3 000 Hz，调制波频率50 Hz，光伏母线电压为400 V。通过测量其单相等效电阻为18.7 Ω，单相等效电感为2.973 mH，电机耦合等效电容为7.83 nF，等效阻抗Z0=378 Ω。

通过上述的参数选取方法，可以选取滤波器的参数为：Rf=Z0=355 Ω，Lf=0.478 mH，Cf=10.1 nF。

图11(a)为无滤波器时的电机侧的定子电流与线电压波形，其输出的有效值分别为：usA=269 V，isA=8.31 A；输出电压频率为50 Hz；电机侧的输出功率为2 996 W；图11(b)为此时光伏水泵系统所产生的共模电压与共模电流波形，从图11中可以看出其共模电流的峰值可以达到2 A。

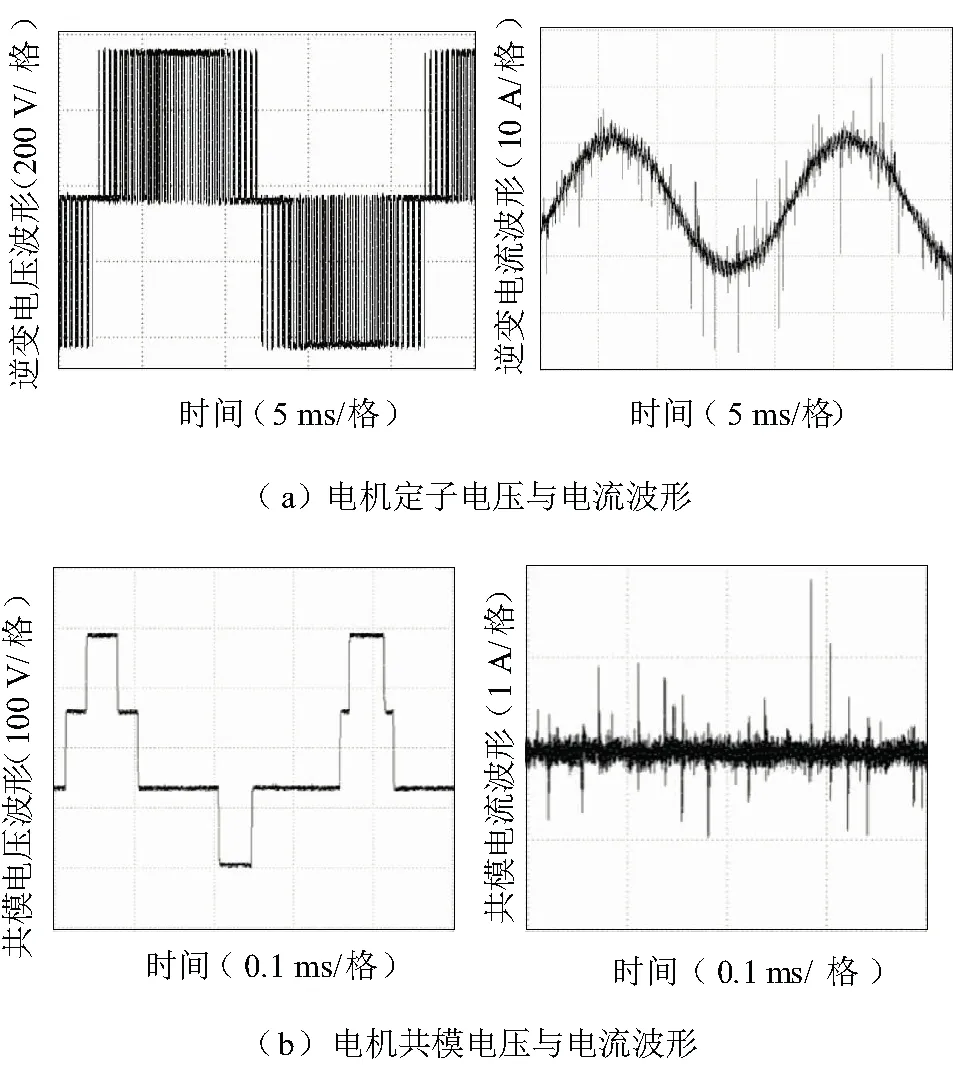
图11 无滤波器时电机的输出状态

图12(a)为添加LC滤波器后采用V/F控制时电机侧的定子电流与线电压，其输出的有效值分别为：usA=241 V，isA=9.213 A；输出电压频率为50 Hz；从中可以看出采用此滤波器后滤波压降为18 V，远小于工程要求，且此时电机的输出功率为2 970 W，电机处于额定运行的状态。即此滤波器对电机的V/F控制几乎没影响。

图12(b)为采用矢量控制时电机侧的定子电流与线电压，其输出的有效值分别为：usA=240 V，isA=8.82 A；输出电压频率为49 Hz；且此时电机侧的输入出功率为2 837 W，电机处于地运行的状态。即此滤波器对电机的矢量控制有影响，但影响较小，电机处于接近额定输出的状态。

图12(c)为此时光伏水泵系统所产生的共模电压与共模电流波形，从图中可以看出其共模电流的峰值低于0.5 A。相对于未加滤波器的共模电流得到了极大的抑制。

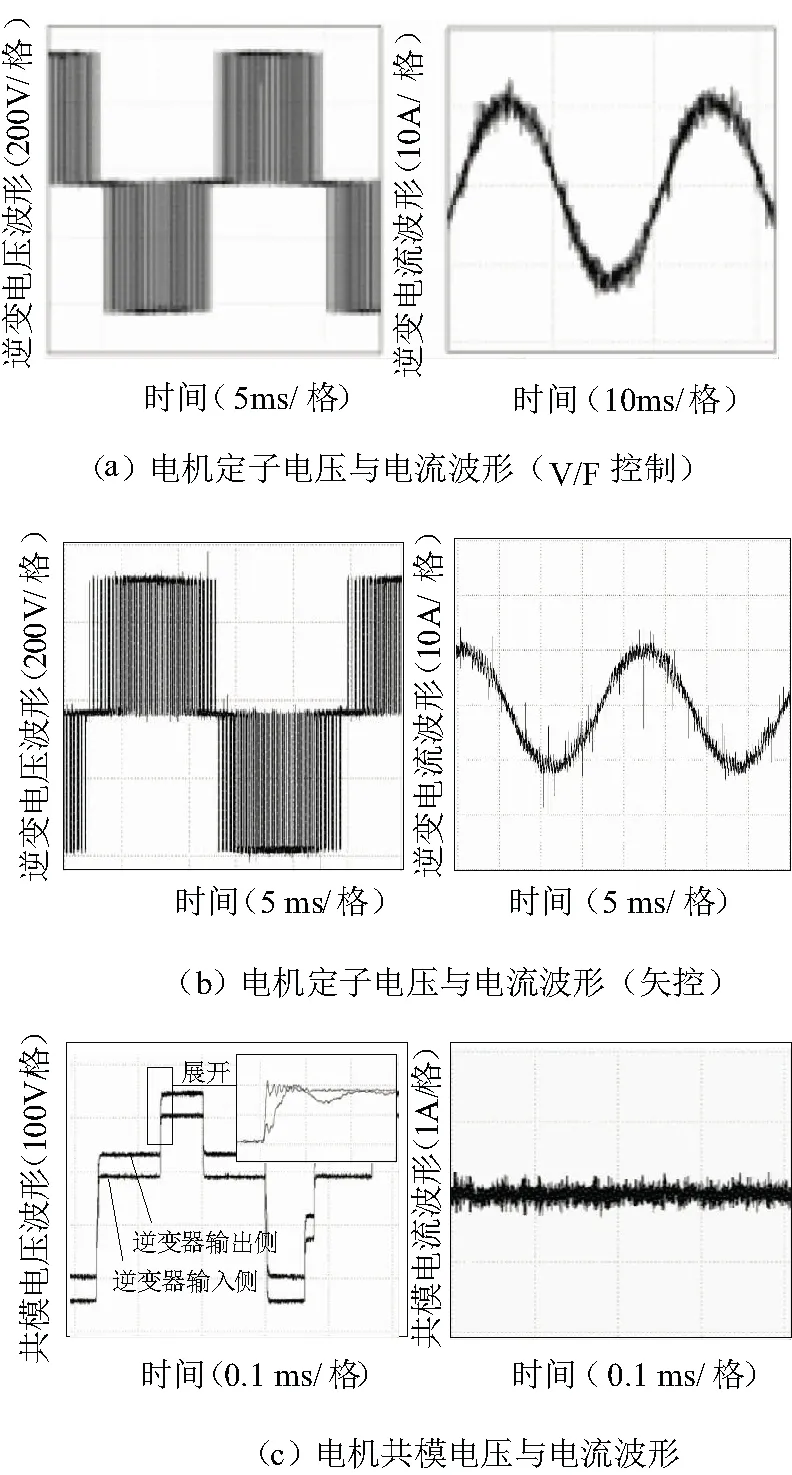
图12 添加滤波器时电机的输出状态

6 结束语

建立了光伏逆变器共模等效模型，分析了产生共模电压与电流的产生机理，采用改进型LC滤波器，将滤波电容公共点和直流侧负端相连，可以有效地滤除电机耦合电容电压中的高频分量，从而有效抑制了共模电流。分析了改进型LC滤波器对电机控制系统的影响，对LC滤波参数的选取进行了优化，实验结果表明，采用改进型LC滤波器后，变器的共模电流大幅衰减；且对电机的V/F控制系统几乎无影响；对电机的矢量控制系统影响较小。