基于Dempster-Shafer证据理论和人工智能的变压器故障诊断研究

何宁辉,沙伟燕,相中华,李秀广,周 秀

(国网宁夏电力有限公司电力科学研究院,宁夏 银川 750011)

变压器是电力系统中的重要环节,其寿命主要取决于其绝缘的机械强度和电气完整性[1]。变压器内部发生的水解、氧化和热裂解均会导致变压器退出运行[2]。通过开展实时故障监测及诊断,能够有效避免过热或电弧等故障的进一步发展,保障变压器的安全运行[3]。

变压器油的溶解气体分析(Dissolved gas analysis,DGA)方法结果可用于故障的监测预警。近年来,采用DGA气体比值作为特征参量,国内外提出了变压器故障诊断的多种判据,如Doernerburg比值[4]、Rogers比值[5],同时,CIGRE[6]、IEC 60599[7]、DL/T 722-2014[8]等也都提出了相应的诊断标准。人工神经网络能够建立DGA与变压器故障之间的复杂非线性关系,但缺点在于网络内部结构类似于“黑匣子”,无解释能力,并且有时收敛速度较慢[9]。模糊专家系统利用模糊规则将专家的经验和知识纳入系统,因此实现对变压器的DGA故障诊断,气体属性的阈值可以划分故障类型,然后对这些数据进行模糊处理,以解决DGA数据的不完整性和不精确性问题[10]。文献[11]中提出基于模糊逻辑的DGA故障诊断方法,识别了变压器的多个故障。文献[12,13]指出部分DGA气体比值不具备变压器故障诊断的能力,采用这些气体比值反而会影响故障诊断的效果。

本文提出了基于Dempster-Shafer证据理论(Dempster-Shafer evidence theory,DST)和人工智能的变压器故障诊断方法。首先对变压器油中的溶解气体进行分析;其次以H2、CH4、C2H4、C2H6和C2H2的浓度百分比作为反向传播神经网络(Back propagation neural network,BPNN)的输入,将其诊断结果作为第一证据;然后再以C2H2/C2H4、CH4/H2和C2H4/C2H6这3种气体比率作为模糊逻辑的诊断依据,将其诊断结果作为第二证据;最后,利用DST对上述结果进行集成分析得到最终的诊断结果。

1 Dempster-Shafer证据理论

Dempser-Shafer证据理论不需要先验概率,具有依靠证据的积累,不断缩小假设集合的能力,在区分不确定性与不知方面具有较大的优势[14]。假设X是一有限集合,X的所有子集的集合是它的幂集2X,存在一个函数m将所有子集映射到[0,1],即m:2X→[0,1],且函数m满足

∑(A⊆)m(A)=1

(1)

m(φ)=0

(2)

式中:φ为空集,A为X的任意一子集,则m(A)表示A的基本可信度分配函数,A的子集称为焦元。

在X上,置信函数定义为:bel:2X→[0,1],且有

bel(A)=∑((B⊆A:B≠φ))m(B)

(3)

式中:bel(A)是A的全部置信度。

在X上,似真函数定义为:pl:2X→[0,1],且有

pl(A)=∑B∩A=φm(B)

(4)

式中:pl(A)表示不反对命题A发生的程度,且pl(A)需要满足条件

{A⊆X∣m(A)>0}≠φ→bel(A)≤pl(A)

(5)

图1为测量置信度和似真性的图示。两者之差定义为集合A的不确定性或证据区间。由图1可知,置信区间由bel(A)表示,似真区间由pl(A)表示,不信区间由1-pl(A)表示,怀疑区间由1-bel(A)表示。

图1 置信度和似真性关系结构图

若bel1和bel2是同一有限集合X上的两个置信函数,则有

(6)

式中:A,B,Z⊆X分子表示支持假设Z的集合A和集合B的累积证据,分母量化了两个集合之间的冲突量。

2 溶解气体分析DGA

DGA被广泛应用于油浸式变压器的健康状况监测。通过对变压器油中溶解气体分析,可以及时发现变压器在运行中的故障。变压器绝缘油中常见的气体有氮气(N2)、氧气(O2)、氢气(H2)、二氧化碳(CO2)、一氧化碳(CO)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)和乙炔(C2H2)。N2和O2的主要来源是大气,H2的主要来源是局部放电,CO2是由过热的纤维素产生,CO的存在归因于过热的纤维素和空气污染,油的热老化会产生CH4、C2H6和C2H4,C2H2的产生是由于油中的电弧放电。因此,变压器故障可主要分为3种类型:局部放电、放电和热故障。放电的能量耗散强度最大,热故障的能量耗散强度较小,局部放电的能量耗散强度最小。

根据IEC/IEEE标准,可以用C2H2/C2H4、CH4/H2、C2H4/C2H6这3种比值来评价正常老化、局部放电、放电和不同严重程度的热故障4种情况。利用标准进行故障诊断是通过与标准中的气体比比率进行比较,并且给出了对应代码。表1为利用IEC/IEEE标准进行故障诊断所需要的气体比的比率及其代码。表2为利用IEC/IEEE标准中的代码并基于BPNN进行的诊断分类,一共为9类,分别是正常、低能量密度局部放电(Partial discharge of low energy density,PDL)、高能量密度局部放电(Partial discharge of high energy density,PDH)、低能放电(Discharge of low energy,DL)、高能放电(Discharge of high energy,DH)、热故障(Thermal fault,TH)<150 ℃、TH 150-300 ℃、TH 300-700 ℃、TH <700 ℃。

表1 IEC/IEEE标准

表2 基于IEC/IEEE和BPNN的故障诊断

随着温度的升高,油纸绝缘系统中的CO2和CO迅速增加。如果CO2/CO<3,则表明故障可能涉及绝缘纸,并具有一定程度的碳化。即使只有极少的C2H2也表明存在高能电弧。高温热故障也可能产生微量的这种气体。一次电弧就可产生C2H2,因此,如果发现C2H2,则应进行频繁采样,如果发现额外的C2H2,则表明存在主动放电。若C2H2的生成速率加快则表明故障更加严重。

3 基于人工智能的变压器故障诊断

3.1 基于BPNN的故障诊断

将人工智能技术应用于变压器故障检测,基于差分遗传算法对变压器故障状态进行评估,为早期故障识别提供了有效的解决方案。传统的BPNN由于具有识别模式的能力而得到了广泛应用。为了使BPNN具有良好的非线性映射能力并且能够进行无监督学习,本文选择S型激活函数和梯度下降法作为其内嵌函数[15]。在仿真编译环境(MATLAB 2019b)下,为了收敛速度慢,本文选择三层神经网络,输入为5种关键气体(H2、CH4、C2H4、C2H6和C2H2)的浓度百分比,输出为6种故障,通过试凑法确定了隐层神经元个数为3,学习率为0.9,最终得到了BPNN的拓扑结构为“5-3-6”。表3给出了这6种故障的输出模式。

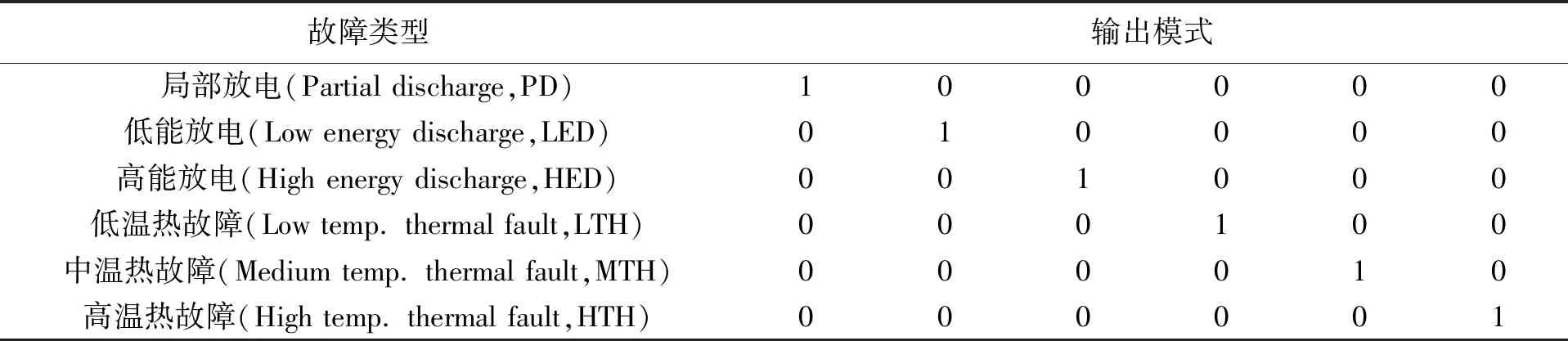
表3 训练数据的输出模式

3.2 基于模糊逻辑的故障诊断

在本研究中采用半柯西分布函数作为隶属度函数,利用模糊逻辑对变压器进行故障诊断。模糊逻辑方法能够正确识别变压器内部发生的多个早期故障,并在IEC/IEEE方法由于可能的比值组合不完整和数据范围没有覆盖而无法预测时进行预测[16]。

上升半柯西分布函数

(7)

下降半柯西分布函数

(8)

式中:C、c分别为边界参数和分布参数,p=2,其余参数值如表4所示,在表4中,w1=min[ur1(0),ur1(2)],w2=min[ur2(1),ur2(2)],w3=min[ur3(0),ur3(2)]。气体比边界的隶属函数ur1定义为C2H2/C2H4,ur2定义为CH4/H2,ur3定义为C2H4/C2H6。

表4 气体比隶属函数的边界和分布参数

3.3 实例验证

DGA样本来自于国网宁夏电力有限公司电力科学研究院所负责的部分变压器。表5给出了采用IEC/IEEE标准分类的DGA样本编号和故障类型的详细信息。其中,训练集169个样本,验证集21个样本,测试集22个样本。由于真实样本中部分故障样本缺失,所以在本研究中将低能量密度局部放电(F1)与高能量密度局部放电(F2)合并,将小于150 ℃的热故障(F5)与150～300 ℃的热故障(F6)合并。

表5 样品信息

当实际故障已知时,利用IEC/IEEE标准进行故障诊断的准确率为97.66%。因此,本文采用IEC/IEEE标准对此方法进行性能检验。本研究中设定故障出现的阈值为0.34。在169个训练集中有38个样本存在两种及以上的故障类型的阈值超过0.34,其中35个样本满足阈值较高的故障类型与IEC/IEEE诊断一致。另外3例中,有2例IEC/IEEE方法诊断为F5,利用BPNN诊断为F1(PD的阈值略高于LTH的阈值),有1例IEC/IEEE方法诊断为F1,利用BPNN诊断为F5(LTH的阈值略高于PD的阈值)。表6给出了其中6组样品的DGA数据。表7为其对应的BPNN归一化输出,其中黑体对应预测的故障类型。

表6 部分样品的DGA数据

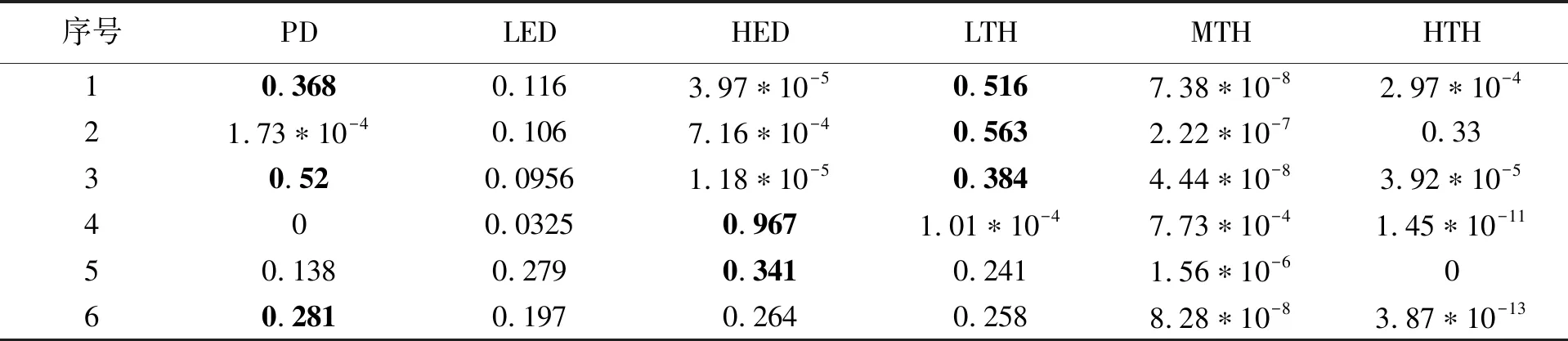
表7 部分样品的BPNN归一化输出

表8给出了应用于样本DGA数据的模糊逻辑归一化值,其中黑体对应预测的故障类型。在DGA上应用半柯西分布函数可以诊断出样本2和样本4中的多个故障。

表9比较分析了上述3种不同方法的故障诊断结果。对于样本1,3种方法都成功预测了热故障。对于样本2,IEC/IEEE诊断为300～700 ℃的热故障,BPNN诊断为低温热故障,模糊逻辑诊断为中低温热故障。对于样品3,所有方法都确认存在局部放电。样品4和样品5的实际故障是放电,BPNN诊断能够成功诊断,而IEC/IEEE无法诊断。对于样本6,实际故障为局部放电,IEC/IEEE无法诊断,BPNN诊断为局部放电,模糊逻辑诊断为低能量放电,所以在这个样本中存在诊断冲突。

表9 不同方法故障诊断的比较

4 基于DST和人工智能的变压器故障诊断

根据前文介绍的DST及基于人工智能的变压器DGA故障诊断研究基础,在此利用人工智能和DST对变压器DGA故障进行诊断研究。证据是基于DGA的人工智能技术检测出的故障类型,假设集是变压器的初始故障状态,数据来源于基于DGA的BPNN和模糊逻辑的诊断结果。BPNN与模糊逻辑相结合,可以较好地解决故障类型预测的可靠性问题,将BPNN的输出赋值给假设集合A,用半柯西分布函数将模糊集的结果赋值给假设集合B。

基于人工智能的诊断方法结果假设了有限通用集合X,其对应的幂集为

2X={∅,{h1},{h2},{h3},{h1,h2},{h1,h3},

{h2,h3},X}

步骤1定义h1是局部放电,h2是放电,h=是热故障。

步骤2第一组证据分配给假设集合A,BPNN的归一化输出为:h1(局部放电,PD),h2(放电,LED 和 HED),h3(热故障,LTH、MTH和HTH)。第二组证据赋给假设集合B,模糊逻辑诊断结果:h1(局部放电,PDL和PDH),h2(放电,DL和DH),h3(热故障,TH<150 ℃、TH 150～300 ℃、TH 300～700 ℃和TH>700 ℃)。表10展示了样品1的置信分配情况。

表10 样品1的置信分配

步骤3建立假设集合A和B的切割集,剔除非焦元,简化组合表。表11展示了样品1的简化组合表。

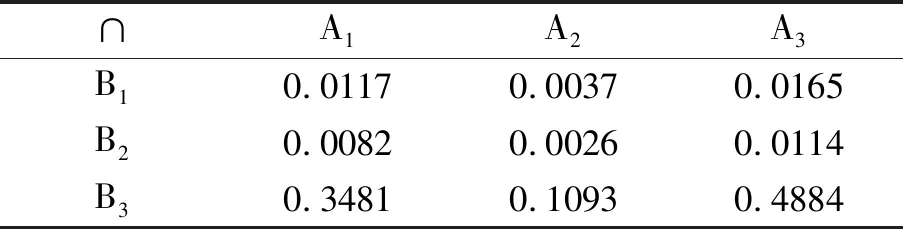
表11 样品1的简化组合表

步骤4从非空集合中计算相关基本赋值乘积(Zk)。相同组合表对应的基本赋值的乘积必须相加。下式展示了样品1的基本赋值乘积。

步骤5通过计算步骤4所有组合的总和来组合基本分配。

步骤6根据步骤1计算组合假设的置信度。下式展示了样品1的所有相关假设集合的基本可信度

m{h1}=0.26021

m{h2}=0.08998

m{h3}=0.65023

步骤7用加权证据置信度映射变压器故障状态。基于此,可得出样品1中变压器内部所发生的故障类型为热故障(h3)。

所得到的样本数据的加权证据置信度以及实际故障与预测故障如表12所示,黑体对应此方法预测的故障类型。对于样本4、6,此方法能够在IEC/IEEE无法诊断的情况下给出的正确诊断。此方法也解决了在样本6中BPNN与模糊逻辑存在诊断冲突的问题。

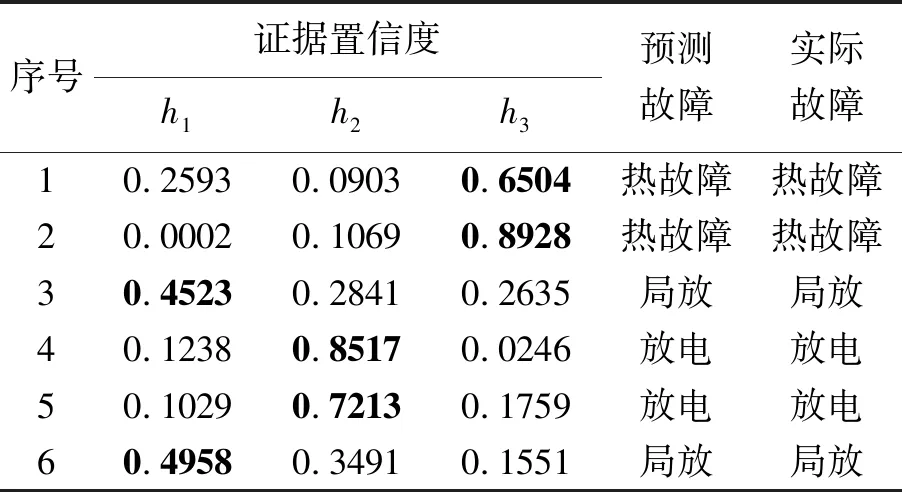
表12 样品的诊断结果

有关变压器历史和测试数据的信息越多,就越有可能正确诊断出变压器的健康状况。当变压器刚投运或已投运但未建立DGA基线信息时,应尽快建立变压器的DGA基线信息,这对随后制定常规监测程序以及应用传统DGA方法进行故障诊断具有十分重要的意义。监控变压器的健康状况必须在日常基础上进行,并且可以随时启动,而不仅仅是针对新机组。为了验证本研究所提出方法的鲁棒性,将这一方法应用于3例变压器的历史数据。

案例1变压器于1971年开始运行,在1989年8月发生放电故障。经修理和除气后,形成了变压器的特殊气体指纹。表13给出了DGA数据,并将所提出的故障诊断方法与IEC/IEEE方法进行了比较。IEC/IEEE方法指出了样本2、3、4的放电故障,而样本1和样本5的故障类型不能被识别。本文所提的方法不仅识别出了样本2、3、4的放电故障,还诊断出了样本1的热故障和样本5的放电故障。

表13 案例1的诊断结果

案例1为同一变压器在不同时间进行采样并诊断,为了突出本文所提方法不仅能成功对DGA数据进行诊断分析,还能实现对在役变压器的监测维修提出指导性的意见,本文绘制了各故障类型的时间-置信度柱状图,如图2所示。从图2中可以看出,当变压器维修后重新投入使用时,机组内部存在二次电弧;样品3、4、5的再次放电证据极高,这个装置需要立即从服务中退出,以防止灾难性故障,并且在此之前需进行密切监测。

图2 故障置信度

案例2110 kV变压器已投运6年,其DGA结果呈现出先增加后稳定的趋势。表14给出了DGA数据,并将所提出的故障诊断方法与IEC/IEEE方法进行了比较。IEC/IEEE方法诊断出了

表14 案例2的诊断结果

样本2～7的热故障,也指出样本1处于正常状态。本文所提的方法也成功识别了样本2～7的热故障。

采用本文提出的方法对样品进行了分析,发现样品中存在热故障,且热故障程度有增加的趋势。从图3可以看出,从热故障初期的增加趋势和增大的置信度可以看出,应在故障初期,导致机组灾难性的失控和故障之前,将变压器退出运行并进行内部检查。结果表明,本文提出的方法可以在一段时间内观察变压器故障的发展趋势。

图3 故障置信度

案例3一台220 kV变压器于1984年9月投入使用。表15给出了DGA数据,并将所提出的故障诊断方法与IEC/IEEE方法进行了比较。第一个样品的DGA测试结果表明油中含有大量气体并且有持续增加的趋势。1996年9月,此变压器停止使用,并进行了内部检查,做了必要的维修和更换,然后将变压器重新投入使用。

从表15和图4可以看出,根据本文所提出的诊断方法,故障的置信度表明样本1中存在放电,样品2～17存在热故障,最后一个样本存在局部放电。

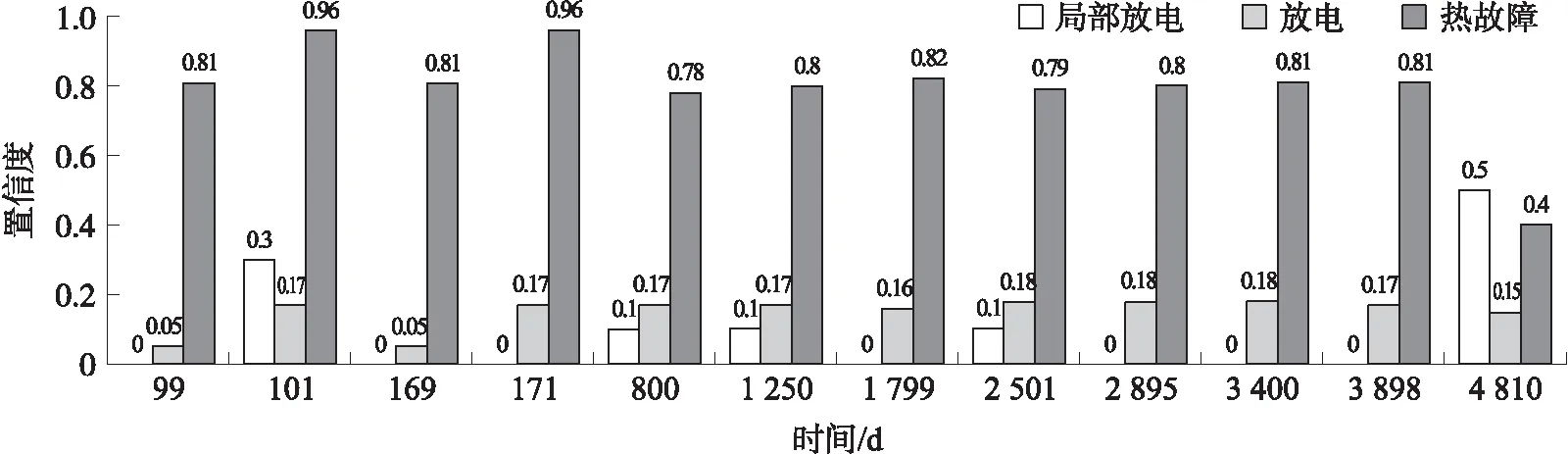
图4 故障置信度

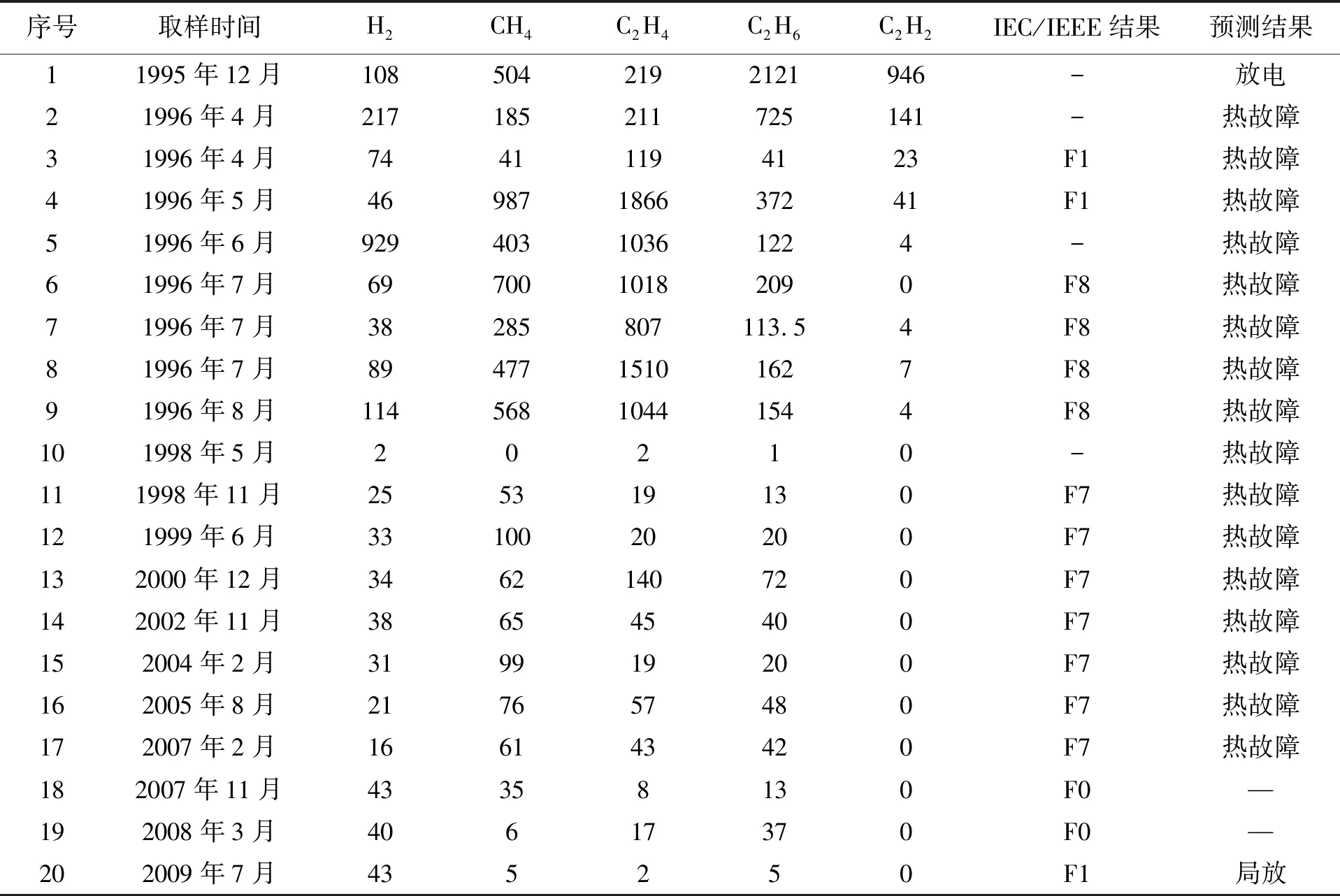
表15 案例3的诊断结果

对比3个案例的结果表明,在案例1中,IEC/IEEE方法成功诊断了其中3个故障,另外两个故障未识别,识别率为60%,而本文所提出的方法成功识别了所有故障,识别率为100%,被两种方法均诊断出的故障类型一致。在案例2中,IEC/IEEE方法成功诊断了所有故障,识别率为100%,而本文所提出的方法成功识别了所有故障,识别率为100%,被两种方法均诊断出的故障类型一致。在案例3中,利用IEC/IEEE方法虽然有小部分故障未识别,但识别出的故障的准确率为100%,而本文所提出的方法成功识别了所有故障,识别率为100%。

5 结束语

本文提出了一种基于DST和人工智能的变压器DGA故障诊断方法,主要得到以下结论:

(1)本文方法以5种关键气体的浓度百分比作为BPNN的输入,并将诊断结果作为第一证据;利用模糊逻辑基于3种气体比率检测变压器故障,并将其作为第二证据;再利用DST对第一证据和第二证据进行联合分析得到最终的诊断结果。对变压器实际DGA数据的测试表明,此方法具有良好的诊断能力。诊断结果与实际故障一致,在传统方法无法识别故障类型的情况下,也能成功识别出变压器的故障类型。

(2)本文提出的基于DST和人工智能的变压器DGA故障诊断方法,为电力行业提供了一种新的变压器DGA故障诊断思路。故障的置信度能够为变压器的日常监测和维护提供良好有效的决策依据。