地下室侧壁及底板在不同边界条件下的实际受力状况分析及设计

郑硕锋

（中建八局华南公司设计研究院 广州 510663）

0 引言

我国大量的民用建筑附建地下室作为车库、设备用房、人防等用途。这些地下室埋深、层高、平面布置、荷载工况、边界条件以及与主体结构的连接方式等形式多样，使得其往往需要考虑多种内外部条件，进行综合分析，才能设计出符合实际受力状态的合理结构。但在实际工程实践中，对地下室计算的力学假定、边界条件的设定过于简单甚至错误的情况屡见不鲜，这导致了不少项目在经过“仔细”计算，“认真”设计后，仍然存在较大安全隐患。这其中，对于地下室侧壁支座条件和力学模型的假定出错，而导致内力分析结果与实际不符的情况比较常见。程懋堃大师提出“计算模型务必反映实际的力学状态”，“已建成的工程，不等于是成功的工程”［1］，应是结构设计人员奉为圭臬的原则。运用Midas Gen 有限元软件，对地下室多种底板厚度情况下，侧壁与各层楼板的实际受力状态进行分析，并与传统常规设计中使用的连续单向板模型的计算结果进行比对，来说明这个问题，并进一步提出一些设计措施和建议，供同行参考。

1 Midas有限元模型设定

1.1 结构布置

选用较常规的、常用尺度的车库地下室进行建模，采用简单的多跨对称结构模型进行分析。具体设定为：2层地下室，顶板覆土1.2 m，地下水位埋深−0.5 m，层高分别为−1 层4.0 m，−2 层3.9 m；整体平面尺寸为48 m×48 m，双向各6 跨，柱网为8 m×8 m（周边侧壁不设扶壁柱），顶板层及−1层采用常规十字梁结构布置，底板采用厚板结构，分别按400 mm，600 mm，800 mm，1 200 mm，1 600 mm，2 000 mm 共6 种厚度进行计算；混凝土等级皆为C35，结构平面布置和各构件尺寸如图1、表1所示。

表1 地下室各楼层结构布置Tab.1 Floor Layout of Basement （mm）

图1 结构平面布置Fig.1 Structural Layout Plan （mm）

1.2 荷载及组合

结构荷载考虑自重、常规楼层荷载（见表2），不考虑人防荷载，地下室外考虑车辆超载15 kN/m2，土体天然重度γG=18 kN/m3，饱和重度γsat=20 kN/m3，侧壁土压力采用静止土压力方法计算，K0取0.5［2］；水压力计算水头为顶板覆土面以下0.5 m；采用水土分算。

表2 地下室各楼层荷载工况（不含自重）Tab.2 Floor Load Conditions（Excluding Deadweight）of Basement （kN/m2）

荷载组合采用2 种组合方式：①考虑所有荷载进行组合，按最不利组合1.3G+1.5L［3］计算；②不考虑作用于侧壁上的土压力（含室外车辆超载引起的土压力）和水压力，仅考虑所有竖向荷载，按最不利组合1.3G+1.5L［3］计算。第二种组合仅用于计算400 mm 厚底板的模型，记为模型A1，此模型用于计算竖向荷载下各层楼板产生的弯矩内力值，以对比确认侧壁上由土压力和水压力产生的弯矩分配到各楼层板上的比例。荷载组合计算简图如图2所示。

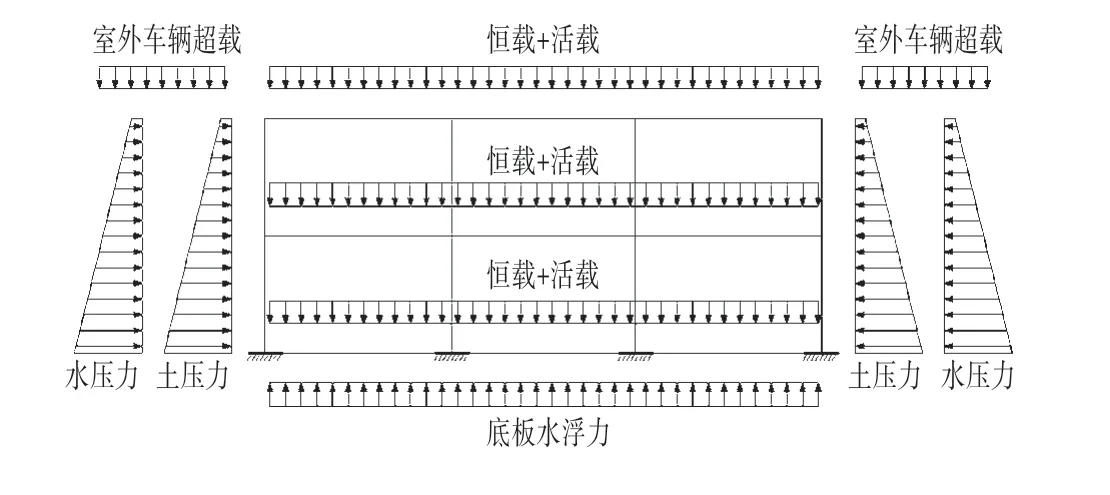
图2 荷载组合计算简图Fig.2 Load Combination Calculation Chart

1.3 边界条件及计算设定

各模型楼层板平面内、外皆按实际刚度计算，柱底支座以强约束模式模拟，A1 模型尚对周边侧壁底部进行全自由度约束，以确保底板在竖向荷载作用下，靠近侧壁的端部弯矩基本由底板承担，尽量减少传递给侧壁。侧壁及楼板皆以板单元模拟，网格划分按0.5 m×0.5 m。

模型按底板厚度400 mm、600 mm、800 mm、1 200 mm、1 600 mm、2 000 mm 分别记为模型A、模型A1、模型B、模型C、模型D、模型E、模型F。又由于实际工程中，有些地下室侧壁设置了扶壁柱，为研究这些扶壁柱对侧壁弯矩内力分布的影响，在模型A 的侧壁上加建扶壁柱（截面同框架柱），记为模型A2。

2 计算与结果分析

2.1 Midas有限元模型研究单元及构件内力分区编号

由于研究对象皆为板构件，故内力分析仅考察弯矩内力图。取模型中间排框架柱往两侧各外扩4 m范围，作为研究单元，如图3所示。又根据弯矩图分布特征，将楼板和侧壁划分为10个弯矩区域，如图4所示。

图3 模型研究单元Fig.3 Unit of Model Research

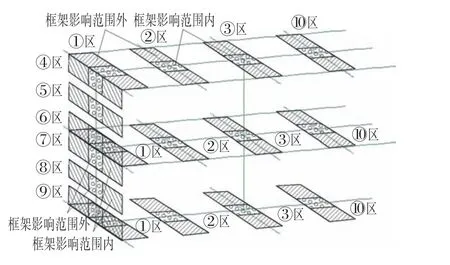
图4 弯矩内力分区编号Fig.4 Area Code for Bending Moment Internal Force

2.2 多种底板厚度下侧壁内力分析比对

2.2.1 梁、柱对侧壁弯矩分布的影响

分析结果显示，模型A2 中的扶壁柱对侧壁有明显的支座效应，侧壁的受力由单向板的受力模式变为类似双向板模式，扶壁柱靠近楼层板位置处，侧壁会有明显的负弯矩出现。侧壁在中间楼层处的负弯矩增大明显（约50%～80%），在顶板和底板处的负弯矩以及楼层中部的跨中正弯矩都有所减小（约10%～40%）。此外，梁与侧壁垂直相交位置，出现应力集中，录得较大弯矩极值，但衰减速度很快，1 个网格单元后便衰减到正常弯矩值的范围。由此可见，梁、柱以及与侧壁垂直相交的墙等构件对侧壁内力的影响很明显。无扶壁柱和带扶壁柱侧壁的弯矩分布如图5所示。为便于对比，减少干扰因素，仅采用无扶壁柱模型进行分析比对，以研究常规计算方法存在的问题。

图5 模型A柱侧壁弯矩分布Fig.5 Distribution of Bending Moment of Model A（kN·m）

2.2.2 多种底板厚度对侧壁弯矩分布的影响

以多跨单向板计算模型（以下称“单向板模型”）对地下室侧壁进行内力计算，侧壁几何、材料条件同Midas 模型（以下称“有限元模型”）设置，荷载按上述第一种荷载组合施加，边界条件按底层固支，中间层连续支座，顶板层分固支和简支两种支撑条件分别计算，结果如图6所示。

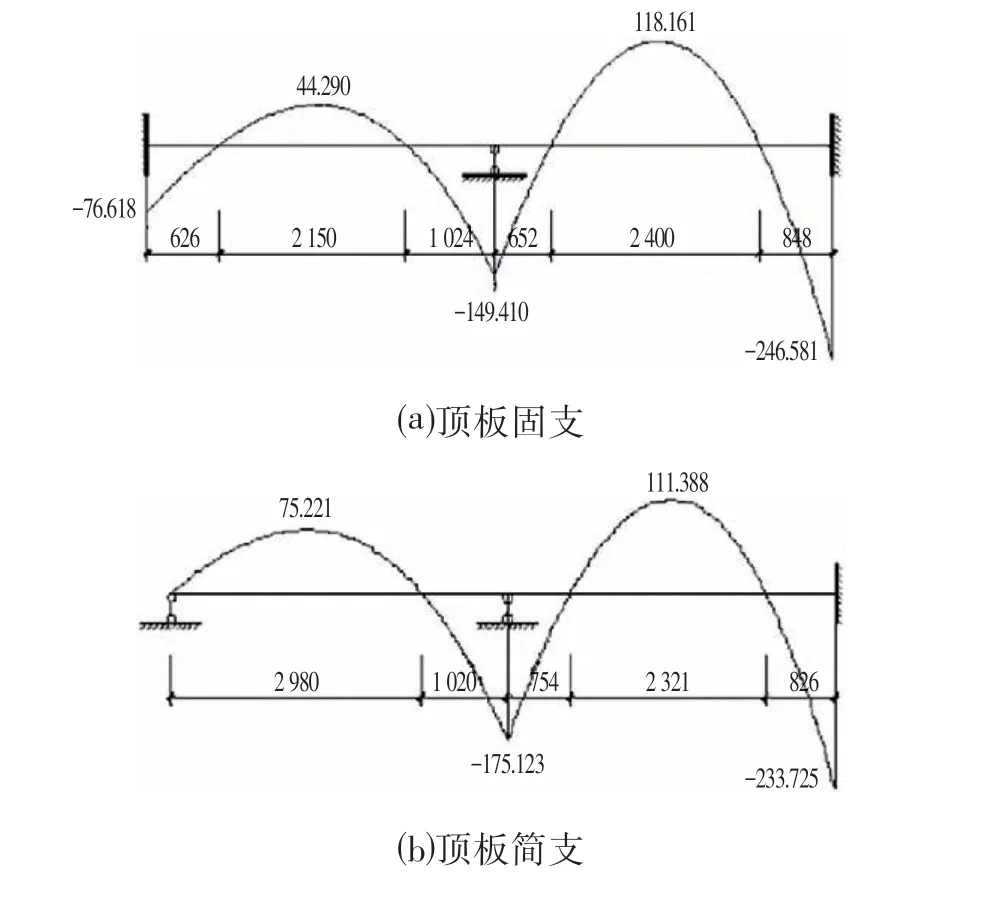
图6 顶板固支的侧壁弯矩分布Fig.6 Distribution of Bending Moment of Roof on Side Wall of Fixed Support （kN·m）

侧壁的支座应根据顶板、底板、墙柱等支撑构件的相对刚度，采用弹性、铰接、固端等相应的支座模型，且在有一定刚度差时，推荐采用铰接支座［4］。这是传统设计方法中很主流的观点，一般认为，顶板的线刚度与侧壁相差较大，实际受力状态应更接近于顶板简支模型，所以常规设计中常常采用顶板简支模型进行计算。

对6 个有限元模型A−F 计算结果进行研究，由于侧壁上框架梁柱影响范围内的弯矩内力值受框架影响，存在应力集中、弯矩极值较大、弯矩突变等情况，故此，仅选取框架梁柱影响范围外的弯矩内力值进行分析比对，如表3所示。由数据对比分析，可以得出以下几方面的推论：

表3 多种底板厚度下侧壁各区域弯矩值Tab.3 The Bending Moment Values of the Bottom Wall under Different Floor Thickness （kN·m）

⑴有限元模型的侧壁底部弯矩值与单向板模型（顶板固支）的结果有较大差异。当底板与侧壁等厚度时，弯矩比值为1∶0.63；当底板厚度不小于2倍侧壁厚度时，弯矩比值在1∶0.89～1∶0.91 之间。主要原因有：①底板必须有远超侧壁的刚度，才能使侧壁底部实现强约束的效果，达到固支的目的；②有限元模型中，底板与侧壁变形协调受力，侧壁底部弯矩被底板分担了不少。由此可知，单向板模型设定的底部固支的边界条件，需底板刚度足够大，能提供较强约束才能勉强实现。

⑵单向板模型计算时，中间楼层板处侧壁计算得到的负弯矩值为−149.4 kN·m（顶板固支），而多个有限元模型对应的弯矩平均值则仅为−32.7 kN·m，前者为后者的4.6倍，计算差异非常明显。分析原因，应该是由于中间楼层梁板面外刚度较小，在多种工况作用下，楼板发生挠曲变形，使得其对侧壁的支撑刚度有一定程度的降低，弯矩更多地被分配到顶板和底板支座处。因此，在常规的计算方法下，中间楼板位置的支座计算弯矩偏大，设计配筋会存在超配情况，应对此处的弯矩进行一定的调幅，并按调幅后的弯矩结果来配筋。

⑶有限元模型中，侧壁顶板支座位置的④号区域，弯矩平均值为−95.7 kN·m，而按顶板固支计算的单向板模型，该区域的弯矩值仅为−76.7 kN·m，前者是后者的1.25 倍。其原因主要有3 点：A.顶板为构件尺寸较大的梁板式结构，其整体面外刚度与侧壁相比，差距并不是非常大，顶板对侧壁形成较强约束；B.顶板竖向荷载较大，使得顶板①区的弯矩比较大，对侧壁提供了较大的转动约束；C.中间楼层支座刚度的减弱，使得部分弯矩传递给了侧壁顶部支座。由此可见，常规的单向板计算模型，对于顶板简支的假定与实际状况存在很大的偏差。有文献采用Sofistik 有限元软件，对地下室进行整体分析，计算结果亦显示侧壁在顶板位置处的弯矩值接近于按顶板固支假定的多跨单向板模型的计算结果［5］。所以，在传统的设计方法中，侧壁按顶板位置简支模型设计，常规300～350 mm 厚度的侧壁，按构造配筋的情况下，所能抵抗的弯矩值不会大于60 kN·m，比本案有限元模型计算得到的弯矩值−95.7 kN·m 小不少，存在较大的安全隐患，需要引起重视。

⑷单向板模型计算得到的楼层跨中正弯矩比有限元模型的结果稍大，但差值基本控制在20%以内，说明按单向板模型设计的楼层跨中正弯矩区域的配筋偏安全，也基本合适。

⑸单向板模型的整体计算弯矩大于有限元模型结果，在一些文献中也得出了类似的结论［5−7］。分析原因，应该是由于单向板模型按支座和构件无限刚度考虑，而有限元模型则按实际刚度计算，同时考虑了变形和支座位移等因素对侧壁内力的影响，部分侧壁弯矩传递给了楼板，所以，侧壁的整体弯矩计算结果比单向板模型的结果偏小。

2.3 多种底板厚度下楼板内力分析比对

2.3.1 侧壁土压力及水压力对楼板弯矩的影响

模型A 及A1，对于顶板、−1 层楼板以及底板的⑩区，两个模型的弯矩值差值比较小，基本都在10%以内；对于底板①区，则差异较大，模型A1①区弯矩平均值约为82.1 kN·m2，而模型A①区弯矩平均值则约为176.1 kN·m2，两者比值达到1∶2.2，②③区的弯矩比值也大致在1∶1.3～1∶1.8之间，如图7所示。

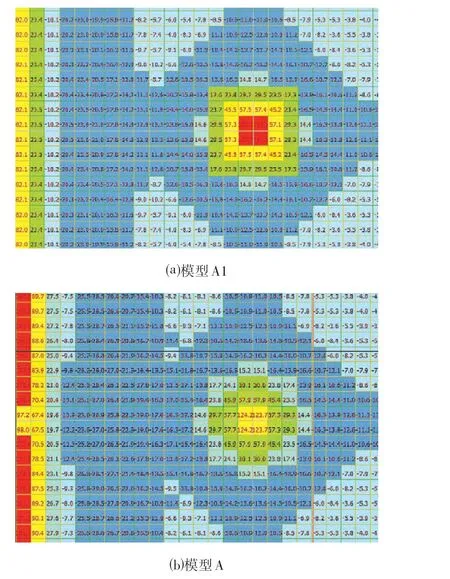
图7 模型底板①、②、③区弯矩分布Fig.7 Bending Moment Distribution of Area ①，②，③of Model Bottom Plate （kN·m）

由此可见，由于底板刚度与侧壁刚度相当，侧壁在土压力及水压力作用下，有较大比例的底部弯矩传递给了底板，其值甚至超过底板竖向荷载作用下产生的弯矩值。但此附加弯矩仅对①、②、③区（即底板第一边跨）有明显影响，随着往远端⑩区推移，其弯矩衰减较快，到达⑩区时，差值已基本衰减到10%以内；而顶板及−1层楼板，与侧壁的刚度差距较大，故侧壁弯矩分配给这两层楼板的比例非常小，对其弯矩值影响不大。

所以，常规的传统计算方法，将侧壁与楼板分开计算、分别设计的方法，存在较大问题，底板的计算结果与实际受力状态相差显著，底板①、②、③区存在较大的安全隐患，实际设计中应予以重视，必须对侧壁与底板进行整体考虑，并采用与实际状态相符的力学模型和软件对其进行计算和设计。前述文献采用So⁃fistik 有限元分析软件对地下室侧壁分别按考虑和不考虑各层楼面竖向荷载影响的两种情况进行分析比对，发现侧壁弯矩在两种情况下相差极大，从而得出楼板与侧壁不能分开单独进行计算的结论［5］，论证方向不同，但观点与本文一致。

2.3.2 多种底板厚度对底板弯矩分布的影响

对模型A−F 楼板弯矩内力图进行比对，底板厚度的变化，仅对其自身的弯矩影响较大，对其余层楼板的内力分布，则完全无影响，故此，选取底板各区域弯矩值进行分析，如表4所示。

由表4 可知：①底板虽为厚板结构，无明梁影响，但由于其基础强约束，底板的弯矩在框架影响范围内仍是有较大的变化，类似无梁楼盖中的柱上板带，出现支座效应；②随着底板厚度增加，底板弯矩随之加大，但底板增大到一定厚度之后（按模型分析，到达最大弯矩值的厚度为1 600 mm，即4 倍侧壁厚度），弯矩就不再增加，且部分区域开始有所回落。有学者提出“外墙厚度一般远小于基础底板，底板计算时在外墙端常按铰支座考虑，而侧壁计算时，在底板端则按固支考虑”［8］，此表述似乎欠妥，从有限元模型的结果可见，侧壁与底板交接位置，弯矩基本为连续的，且弯矩值较大，不能简单按铰支座考虑。

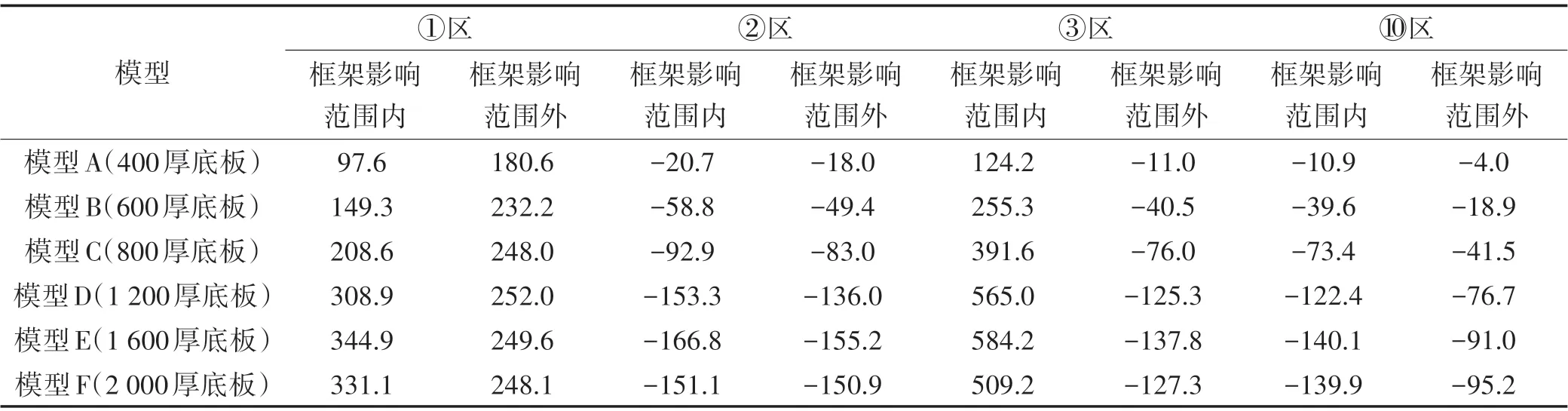
表4 多种底板厚度下底板各区域弯矩值Tab.4 The Bending Moment Values of the Bottom Plate under Different Floor Thickness （kN·m）

3 设计建议

通过以上模型比对分析，根据其弯矩内力的分布状况，对实际工程中地下室侧壁和底板的设计，提出以下建议：

⑴单向板模型和有限元模型计算存在较大的差异，建议采用有限元模型，合理确定边界条件和各构件的本构关系，综合考虑刚度、变形、位移等影响进行分析计算。

⑵若采用单向板模型计算，侧壁底部应按固支考虑，且应确保底板具备足够的厚度，常规地下室，建议板厚至少需达到底部侧壁厚度的2 倍以上，但同时应注意底板厚度的持续加厚，会导致板刚度过大从而分担了更多的弯矩，造成不必要的成本上升，所以，底板厚度应控制在一个合适的范围。此外，底板计算时，应考虑侧壁传递过来的弯矩，对底板第一边跨的配筋予以加强。

⑶若采用单向板模型计算，中间层楼板建议按楼板刚度匹配合适的弹簧支座，对楼板的变形或刚度削弱进行一定程度的模拟，避免中部楼层支座位置分配过多的弯矩，与实际受力存在较大差异。

⑷若采用单向板模型计算，顶板楼层的支座约束应模拟为固定支座进行计算和设计。

⑸梁、柱、垂直相交墙等构件，对侧壁和底板弯矩的分布有较大影响，实际设计中应根据构件的布置情况采取合理的计算模型，同时考虑应力突变的情况予以加强，不应一律按单向连续板的模型进行计算。

4 一些引申

以上分析和设计建议，仅对常规尺度、常规布置的地下室的一般情况进行讨论。实际工程项目中，对于侧壁和底板的内力计算，除了底板厚度以及梁、柱、墙等构件存在较大的影响外，尚有不少其它因素不可忽略，应对这些实际情况进行综合分析，采用合理的计算模型进行计算。这些因素大致有以下几种：

⑴靠近地下室侧壁布置地下室车道时，车道板对侧壁的支撑形式存在很大的改变，此情况下必须采用有限元模型进行空间建模，周全、充分地考虑。罗宁等人［9］对在靠近侧壁位置设置了车道的地下室进行了有限元分析，结果显示车道板对地下室侧壁和相邻跨框架柱的受力产生了非常明显的影响。

⑵实际工程中，侧壁的布置很多时候并不规则，侧壁转角变化、楼板局部位置错层变化或楼板开有较大尺度的洞口等情况，对侧壁的支撑模式往往会造成比较大的改变，实际计算中应充分考虑实际的边界条件，选用合理的计算模型。阮永辉等人［10］研究了地下室楼层错层和开较大洞口的两种情况，分别对侧壁的受力状态进行有限元分析，结果显示侧壁内力变化明显，传力途径怪异。

⑶当侧壁与上部主体结构的竖向构件重叠时，侧壁可能从以受弯为主的大偏心受压构件，变成以受压为主的小偏心受压构件，其截面配筋的计算方法已经发生变化，但实际工作中对此情况往往未作考虑。

⑷地下室的尺度、楼层高度、层数以及柱网、楼板厚度、梁板布置等几何条件与本案存在较大差异时，则应根据实际的结构布置情况，视复杂程度，采用能准确反映客观情况的软件和模型进行计算。

⑸底板在基础位置的强制约束，适用于有较大直径、能够提供较大抗弯刚度的桩基类深基础，而对于防水板+浅基或者较薄筏板等其它情况，基础约束刚度不足的，应力和弯矩集中现象不会这么明显，整体的弯矩将会向跨中转移，实际设计中应根据客观情况，采用相应的、合适的应对方法。