基于Copula函数的汉江流域降水径流丰枯遭遇研究

王飞宇，张彦，王偲，应其霖，陈婷，于飞龙

基于Copula函数的汉江流域降水径流丰枯遭遇研究

王飞宇1，张彦2*，王偲3，应其霖4，陈婷5，于飞龙3

（1.中国科学院 地理科学与资源研究所 陆地水循环及地表过程院重点实验室，北京 100101；2.中国农业科学院 农田灌溉研究所，河南 新乡 453002；3.江苏省水文水资源勘测局，南京 210009；4.国网东北分部绿源水力发电公司，沈阳 110170；5.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

【目的】汉江作为长江最大的支流，探究其流域内降水径流丰枯遭遇风险对汉江流域水资源科学管理具有重要意义。【方法】基于汉江流域4个水文站径流及其控制流域的降水数据，利用二维和三维Copula函数构建降水径流丰枯遭遇联合分布模型，分析了流域降水径流丰枯遭遇风险概率。【结果】汉江上游石泉站和白河站径流量及控制流域降水量间的丰枯同步概率较大，分别为73.06%和73.45%，中游黄家港站丰枯异步概率最大，达45.21%；汉江上中游石泉站、白河站和黄家港站丰枯同步概率呈现出同枯＞同丰＞同平，而下游仙桃站为同平＞同枯＞同丰。汉江上中游石泉站、白河站和黄家港站组合下控制流域降水量间的丰枯同步概率较大，为72.88%；流域内不同站点组合下控制流域降水量的丰枯同步概率呈同平＞同枯＞同丰，径流量的丰枯同步概率均呈同枯＞同丰＞同平。【结论】汉江流域上游径流量及控制流域降水量的丰枯一致性较好，下游的丰枯一致性相对较好，而中游的丰枯一致性较差；不同站点组合下控制流域降水量的丰枯具有相对较好的一致性，而径流量的丰枯同步、丰枯异步概率差异性不显著。

汉江流域；Copula函数；降水径流；丰枯遭遇；风险概率

0 引言

【研究意义】受全球气候变化和人类活动的影响，流域水循环过程发生显著变化，改变了流域降水径流关系，对流域水资源管理及社会经济发展造成影响[1]。降水径流丰枯遭遇的实质就是同一区域或不同区域间气象水文变量的组合问题[2]，明晰流域内降水径流发生丰水或枯水的概率可为流域水资源规划管理提供理论依据。【研究进展】目前，Copula函数在洪水频率计算[3-4]、水沙丰枯遭遇分析[5-6]、干旱特征分析[7-8]、水资源供需风险[9]、降水频率计算[10-11]、水质水量联合分布[12-14]以及水生态环境稳态关系[15]等方面得到了广泛的应用，如李子远等[16]利用Archimedean Copula函数分析了黄河和清水河洪峰发生时间和量级遭遇的风险；何英等[17]、李荣波等[18]和范嘉炜等[19]利用Copula函数分别在叶尔羌河流域、长江流域和潖江河大庙峡流域计算了洪峰流量与洪水历时的联合频率；王深等[20]利用Copula函数建立了渭河流域多水库联合洪水风险分布；谢华等[21]利用Copula函数计算了长江、淮河和黄河流域径流量的联合概率和条件概率；梁希金等[22]利用三维Copula函数构建了多变量联合概率模型并分析了雅砻江、鲜水河和庆大河的洪水遭遇风险；陈心池等[23]利用多种Copula函数筛选了汉江中上游流域降水和洪水联合分布的最优概率模型；马盼盼等[24]选用Copula函数分析了汉江干支流径流的丰枯遭遇组合概率。【切入点】结合汉江流域受到气候变化和人类活动的影响以致其水文情势比较复杂的现实状况，开展降水径流丰枯遭遇研究对汉江流域水资源合理开发利用具有重要意义。【拟解决的关键问题】本文基于1965—2018年汉江流域石泉站、白河站、黄家港站和仙桃站等4个水文站的实测径流数据及流域内气象站点降水数据，首先优选构建流域内降水量和径流量的边缘分布函数，其次利用Copula函数构建流域内各水文站降水径流的二维和三维联合分布模型，进而分析汉江流域降水径流丰枯遭遇的风险概率，研究成果以期为汉江流域水资源管理、防灾减灾规划和社会经济发展提供理论参考和决策支持。

1 材料与方法

1.1 研究区及数据来源

汉江（106°E—114°E，30°N—34°N）是长江最大的支流，同时也是南水北调中线工程、引汉济渭等跨流域调水工程的水源地，其起源于陕西省汉中市宁强县，在湖北省武汉市汇入长江，全长约1 577 km，流域面积为15.9万km2，约占长江流域总面积的9.2%[25-26]。汉江流域地处亚热带季风区，气候温和湿润，年平均气温为16 ℃，多年平均降水量为887 mm[27]。汉江流域以丹江口以上为上游，地形起伏较大；丹江口至钟祥为中游，地势相对平坦；钟祥以下为下游，地势平坦形成了江汉平原。

本文基于汉江流域66个气象站点1965—2018年逐月降水资料，以及石泉站、白河站、黄家港站和仙桃站等4个水文站同时期逐月实测径流数据，利用Copula函数构建了降水径流丰枯遭遇联合分布模型，分析了流域降水径流丰枯遭遇风险概率。降水资料来源于中国气象数据网（http://data.cma.cn），对于缺失的降水数据采用线性内插或外延方法进行插补延长。4个水文站径流数据来源于水文年鉴和长江水利委员会水文局，其中石泉站和白河站位于汉江上游，黄家港站位于汉江中游，仙桃站位于汉江下游。水文站控制流域的面均降水量采用泰森多边形法推求。汉江流域气象站点和水文站点分布示意图如图1所示。

图1 汉江流域水文气象站点分布示意图

1.2 研究方法

1.2.1 降水量和径流量丰平枯划分

目前针对流域降水量和径流量丰平枯水平年划分的方法包括基于保证率划分和距平百分率划分[28-30]。为了确保流域年降水量和径流量划入各等级的年数不能过小，本文在中长期定性预报等级表的基础上将流域降水量和径流量根据距平值大小分为丰、平、枯3个等级，距平值小于-10%为枯，距平值在-10%至10%之间为平，距平值大于10%为丰（如表1所示）。

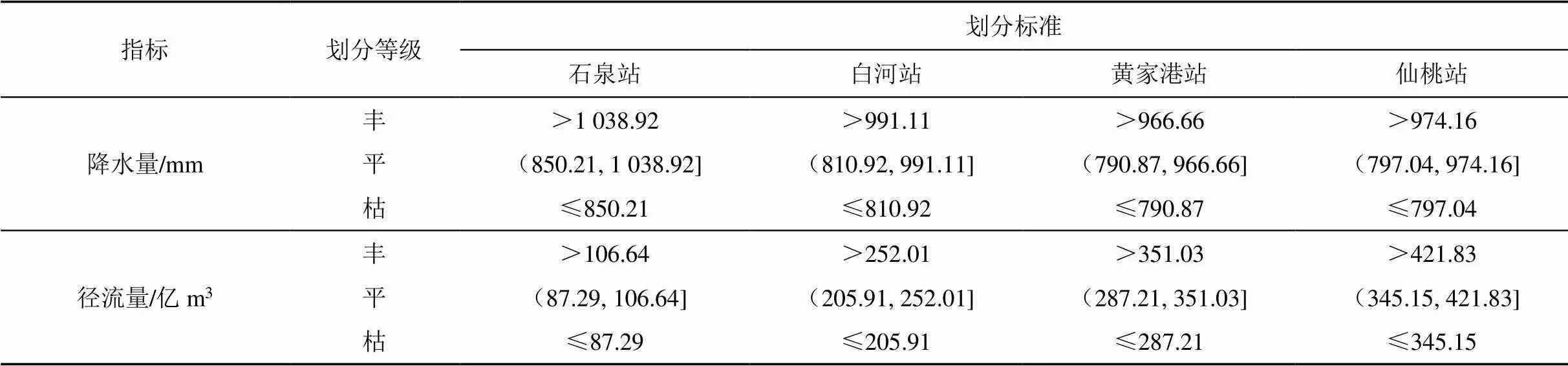
表1 各水文站径流量及控制流域降水量丰平枯划分

1.2.2 降水量和径流量边缘分布函数建立

在利用Copula函数建立降水量和径流量的二维或三维联合分布函数时，首先需构建变量的边缘分布函数。本文基于指数分布、伽马分布、对数正态分布和威布尔分布等单变量分布函数形式对各水文站径流及控制流域降水量进行拟合，并利用Kolmogorov-Smirnov（K-S）检验确定最优的边缘分布函数。降水量和径流量间的相关性采用Kendall秩相关系数和Spearman秩相关系数[31-32]来衡量。

1.2.3 Copula联合分布类型

目前Copula函数有多种联合分布类型，本文的二维联合分布函数主要采用Gaussian、Frank、Clayton、Gumbel和Copula等5种Copula函数形式，三维联合分布函数主要采用Gaussian和Copula等2种Copula函数形式，其二维和三维Copula函数联合分布类型具体的表达式详见文献[33]。

1.2.4 Copula函数拟合检验和拟合优度评价

Copula函数的选取需依据Copula函数的拟合优度检验,本文选用K-S检验对Copula函数进行拟合优度检验。拟合优度评价方法选取均方根误差法（RMSE）、AIC准则法和BIC法[33]，其准则均为值越小，拟合优度越好。其中利用K-S对Copula函数拟合优度检验的统计量计算式为：

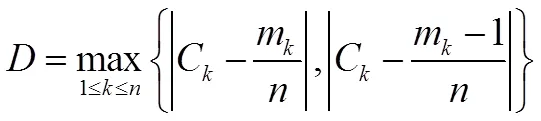
式中：C表示为联合观测样本x=（1k,2k,3k）的Copula函数值；m为联合观测样本中满足≤x，即同时满足1≤1k，2≤2k，3≤3k的联合观测值的个数。

1.2.5 基于Copula函数的丰枯联合风险概率计算

本文根据建立的二维及三维联合分布函数，参照相关文献[28]推导出二维、三维丰枯联合风险概率计算公式如表2所示，其中二维丰枯遭遇类型主要有同丰、同平、同枯、一丰一平、一丰一枯和一平一枯6种，三维丰枯遭遇类型主要有同丰、同平、同枯、一丰一平一枯、一丰二平、一丰二枯、二丰一平、二丰一枯、一平二枯和二平一枯9种。

表2 二维、三维丰枯联合风险概率计算公式

注 在二维丰枯联合风险概率计算中，丰与枯分别表示某一水文站所控制流域降水量的丰与平、枯与平的临界值，丰与枯分别表示同一水文站径流量的丰与平、枯与平的临界值；在三维丰枯联合风险概率计算中，丰、丰和丰分别表示第一、第二和第三水文站所控制流域降水量（径流量）丰与平的临界值，枯、枯和枯分别表示第一、第二和第三水文站所控制流域降水量（径流量）枯与平的临界值。

2 结果与分析

2.1 边缘分布建立

根据指数分布、伽马分布、对数正态分布和威布尔分布等边缘分布函数，对各水文站径流量及控制流域降水量的边缘分布函数进行K-S检验,可得各水文站径流量及控制流域降水量对数正态分布函数为最优概率分布函数（图2）。对各水文站径流量及控制流域降水量的分布函数进行Spearman和Kendall秩检验可知，各水文站径流量及控制流域降水量间的Spearman秩相关系数均大于0.75，Kendall秩相关系数都大于0.53，且2种秩相关系数在0.01水平（双侧）上显著相关；各水文站控制流域降水量间的Spearman秩相关系数均大于0.75，Kendall秩相关系数基本上都大于0.51，且2种秩相关系数在0.01水平（双侧）上显著相关；各水文站径流量间的Spearman秩相关系数均大于0.77，Kendall秩相关系数基本上都大于0.59，且2种秩相关系数在0.01水平（双侧）上显著相关。上述研究表明各水文站径流量及控制流域降雨量间以及各水文站径流量间或控制流域降水量间均具有较高的相关性，可利用Copula函数构建各水文站径流量和控制流域降水量间的联合分布函数。

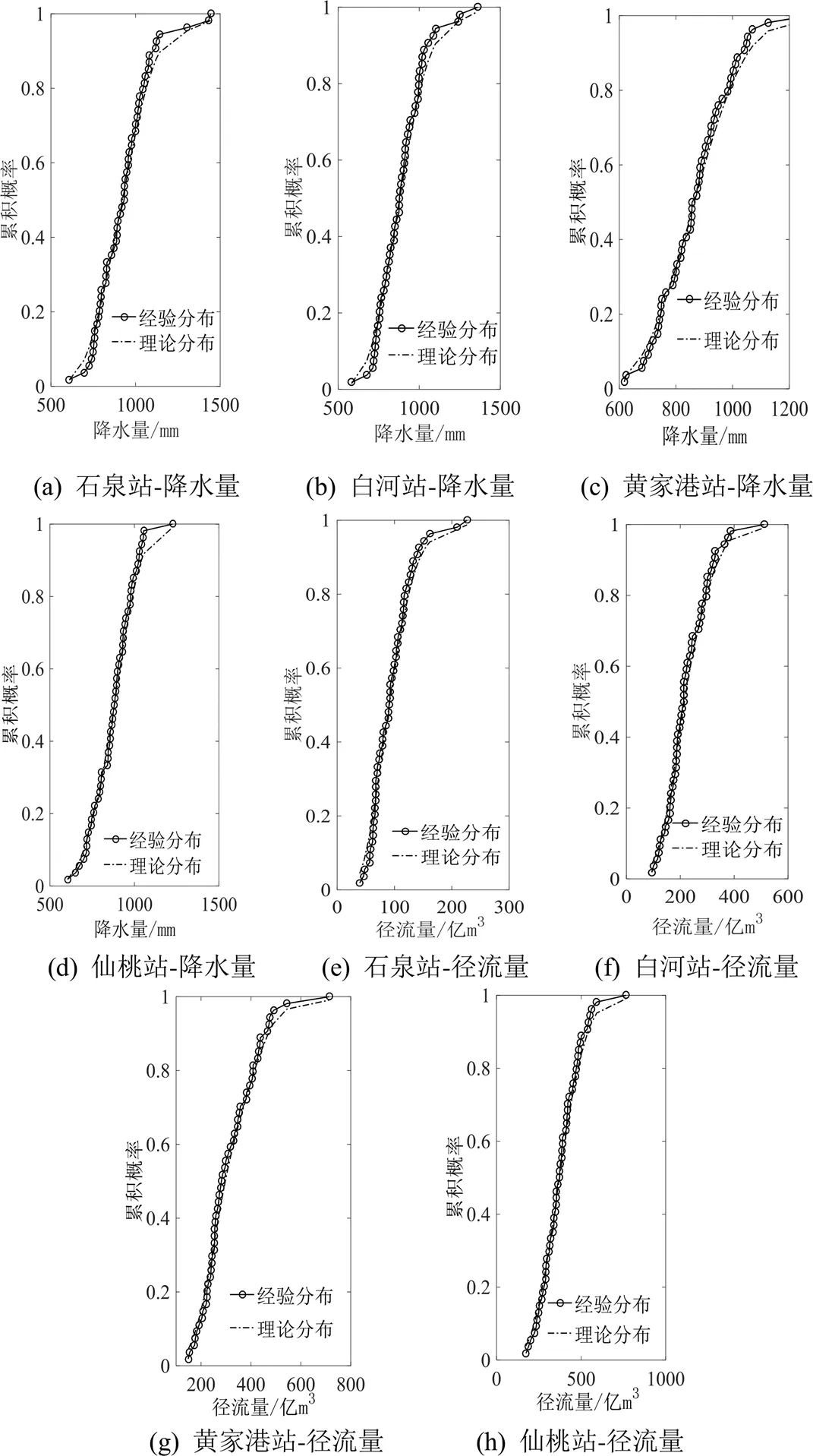
图2 各水文站径流量及控制流域降水量的经验和理论边缘分布

2.2 Copula函数的选择

本文选用Gaussian、Frank、Clayton、Gumbel和Copula函数构建汉江流域各水文站径流量和控制流域降水量间的二维联合分布模型，采用Gaussian和Copula函数构建各水文站径流量或控制流域降水量间的三维联合分布模型。二维和三维联合分布模型的参数估计、K-S检验以及拟合优度评价结果分别如表3和表4所示。由表3和表4可知，取K-S检验的95%置信水平（<（=54，=0.05），各水文站不同Copula函数的统计量均小于0.2617，表明所选Copula函数均通过了K-S检验。

利用均方根误差法（RMSE）、AIC准则法及BIC法对各Copula函数进行拟合优度评价。由表3可知，对于各水文站径流量和控制流域降水量间的二维联合分布模型，石泉站、黄家港站和仙桃站Gumbel Copula函数的RMSE、AIC和BIC值最小，表明Gumbel Copula函数拟合优度最好；白河站Frank Copula函数的RMSE、AIC和BIC值最小，表明Frank Copula函数拟合优度最好。

对于各水文站降水量间的三维联合分布模型，站点组合I、II、III下Copula函数的RMSE、AIC和BIC值最小，故Copula函数拟合优度最好；站点组合IV下Gaussian Copula函数的RMSE、AIC和BIC值最小，故Gaussian Copula函数拟合优度最好。对于各水文站径流量间的三维联合分布模型，站点组合I、II、III、IV下Gaussian Copula函数的RMSE、AIC和BIC值均最小，故Gaussian Copula函数拟合效果最优。因此，分别选择拟合优度最好的Copula函数构建各水文站径流量和控制流域降水量间的二维联合分布模型以及各水文站径流量或控制流域降水量间的三维联合分布模型。

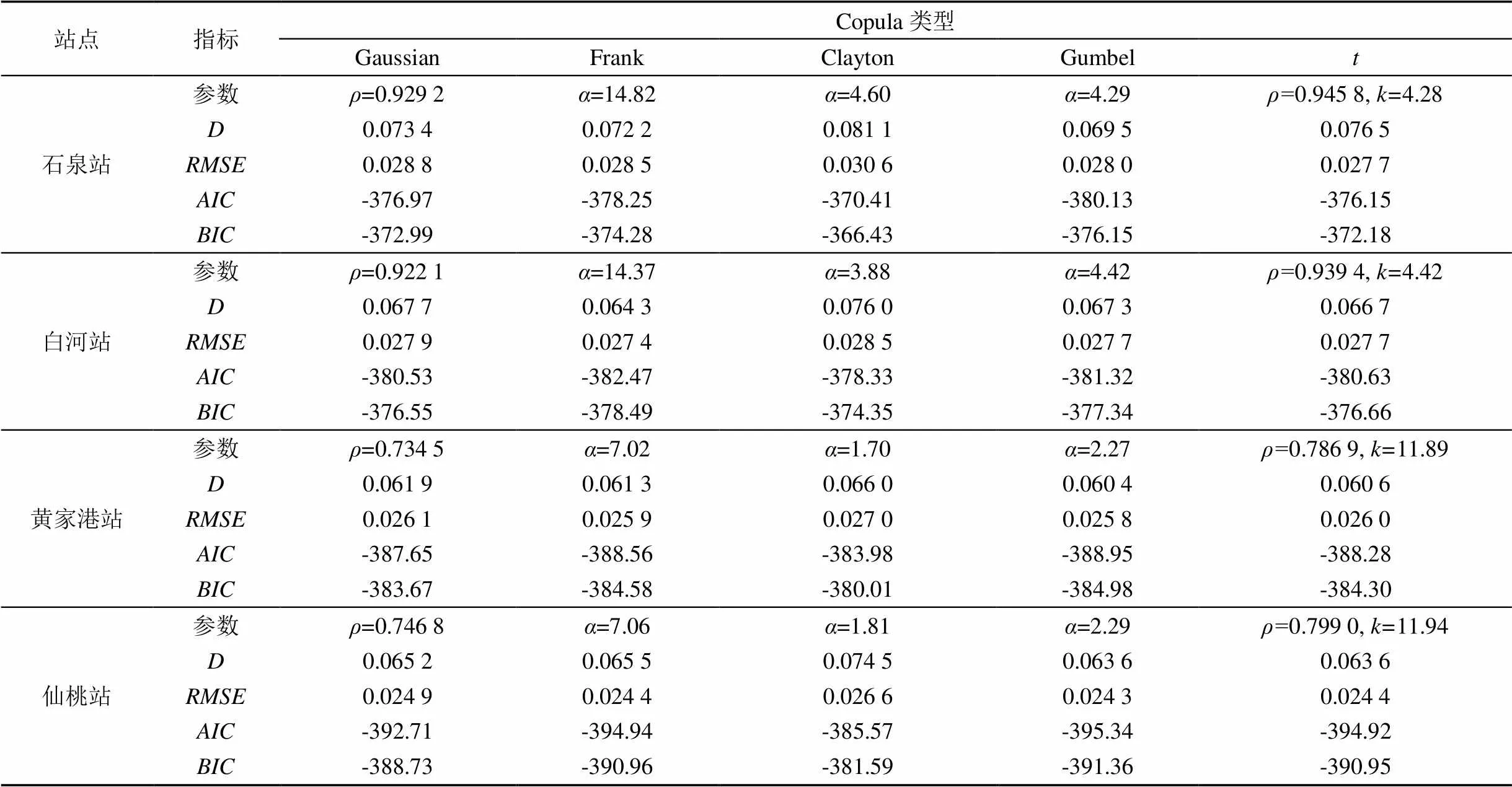
表3 各水文站径流量及控制流域降水量间的二维联合概率分布拟合优度评价

注为对角线上的元素全为1的2阶对称正定矩阵；为Copula函数中描述2个变量相互关系的参数；为自由度。

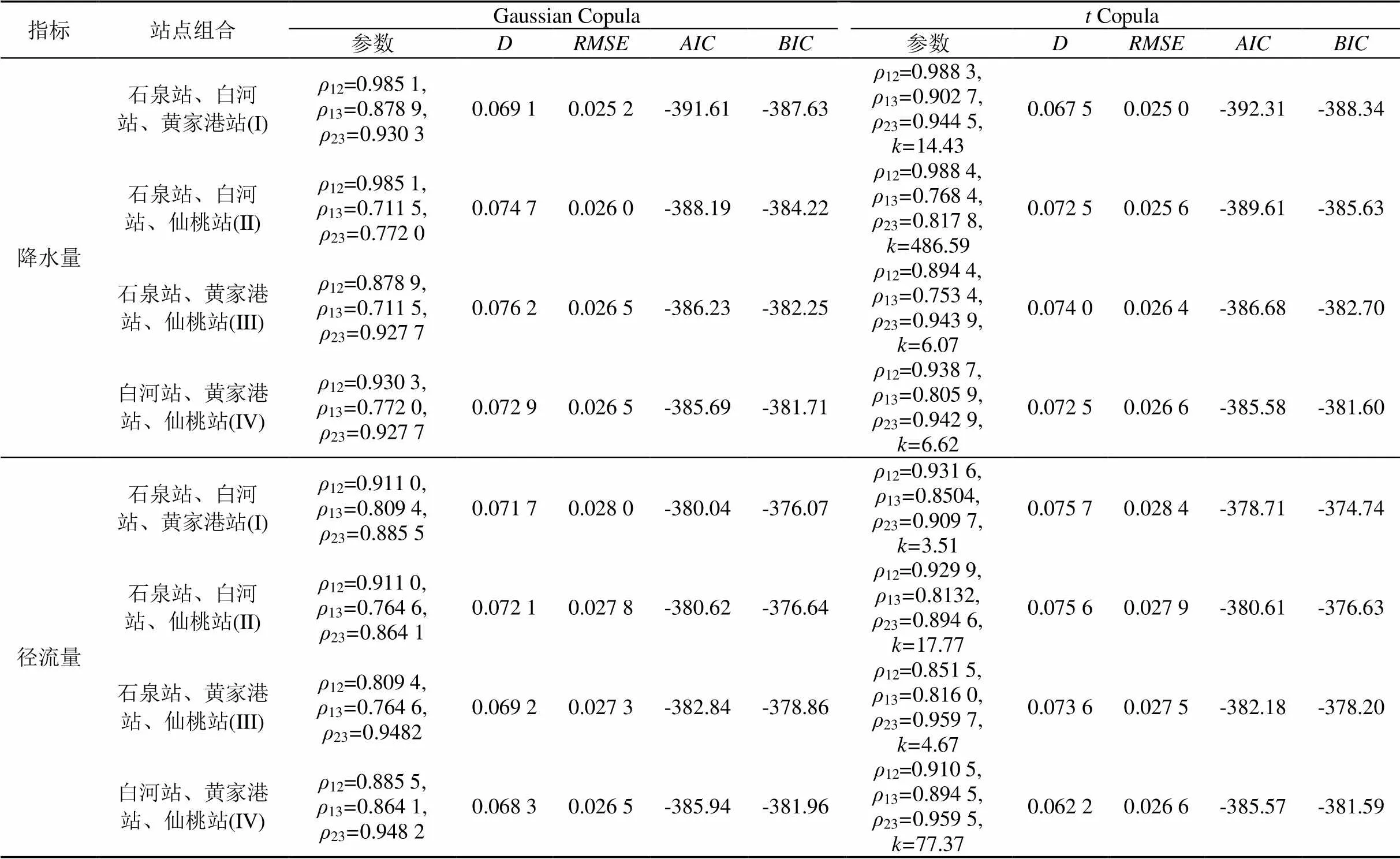
表4 各水文站径流量或控制流域降水量间的三维联合概率分布拟合优度评价

注为对角线上的元素全为1的3阶对称正定矩阵；为Copula函数中描述3个变量相互关系的参数；为自由度。

由图3和图4可知，各水文站径流量和控制流域降水量间的二维联合概率函数以及各水文站径流量或控制流域降水量间的三维联合概率函数的理论频率与经验频率值的拟合情况均较好，表明构建的二维和三维联合分布模型较为合理。

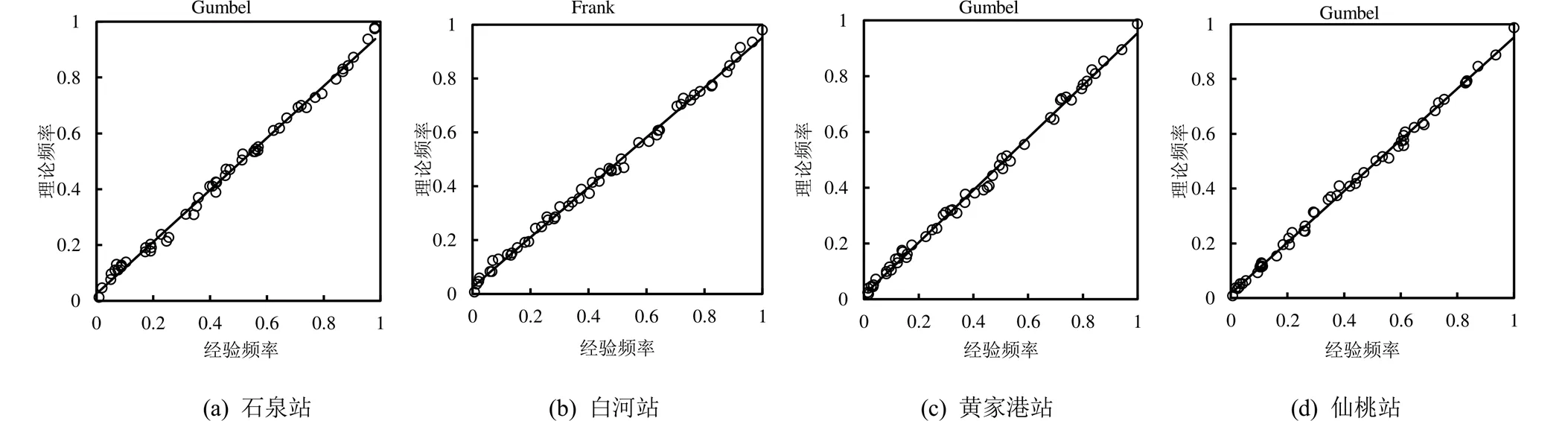
图3 各水文站径流量及控制流域降水量间的理论与经验频率拟合图

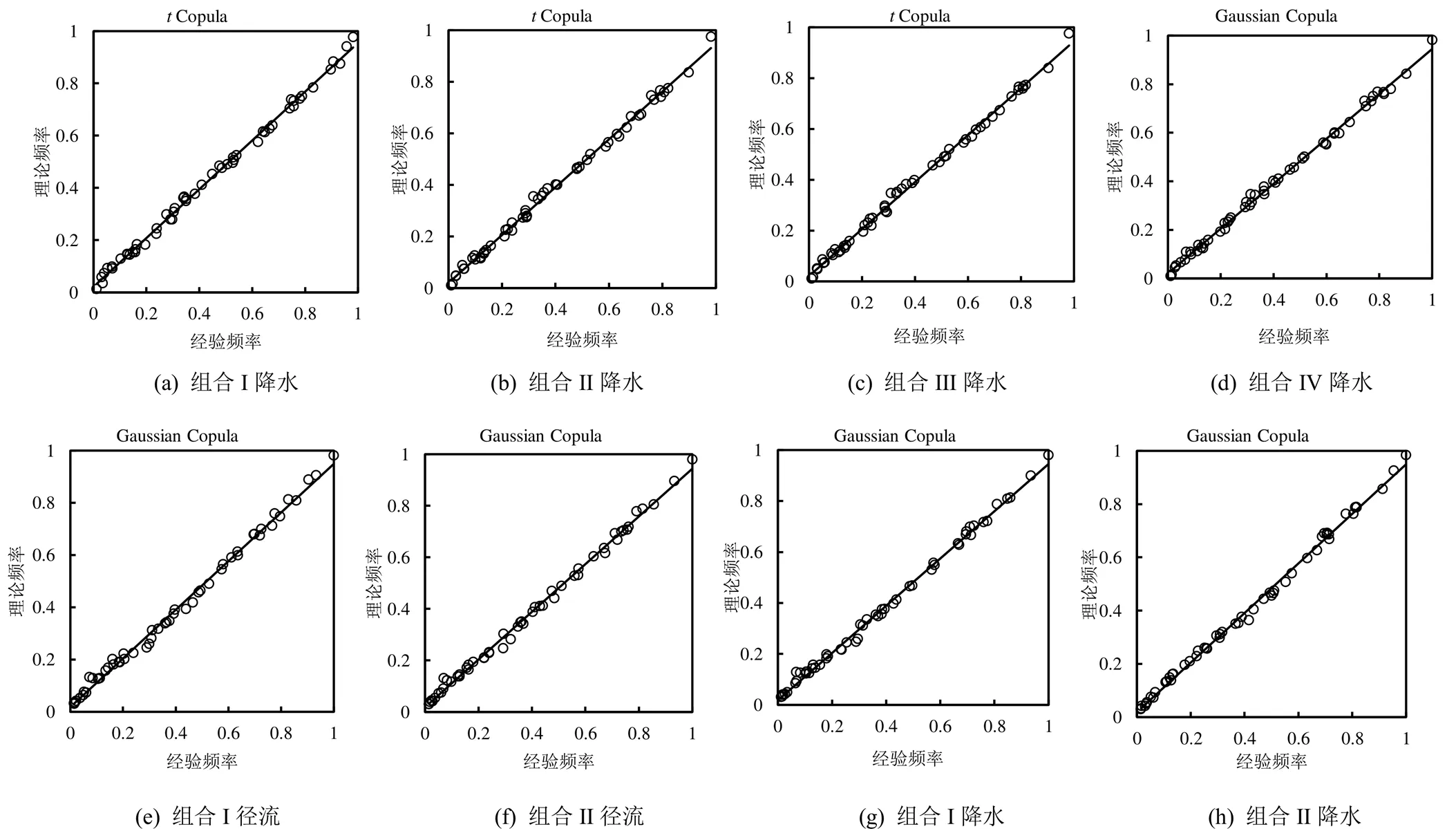
图4 各水文站径流量或控制流域降水量间的理论与经验频率拟合图

2.3 丰枯遭遇风险分析

2.3.1 各水文站径流量及控制流域降水量间的丰枯遭遇风险概率

基于优选的Copula函数建立各水文站径流量及控制流域降水量间的二维联合分布模型，得到各水文站径流量及控制流域降水量的联合分布概率(≤,≤)（图5）。

由图5可知，在各水文站径流量和控制流域降水量都增大时，其联合分布概率值均呈增大的趋势，且增大趋势呈现先缓后急速增加最后变缓的过程。根据表2中二维丰枯联合风险概率的计算公式计算各水文站径流量及控制流域降水量间的丰枯遭遇风险概率。由表可知石泉站、白河站径流量及控制流域降水量的丰枯同步概率均较大，分别为73.06%和73.45%；仙桃站次之，为60.73%；黄家港站最小，为54.79%。而黄家港站径流量及控制流域降水量的丰枯异步概率最大，为45.21%；仙桃站次之，为39.27%；石泉站和白河站均较小，分别为26.94%和26.55%。综上所述，汉江流域上游水文站径流量及控制流域降水量的丰枯一致性较好，下游丰枯一致性相对较好，而中游丰枯一致性较差。另外，汉江中游黄家港站径流量和控制流域降水量的丰枯同步、丰枯异步的概率接近且丰枯同步的概率稍高，表明黄家港站受到人类活动的影响较大，如丹江口水库调蓄的影响等。

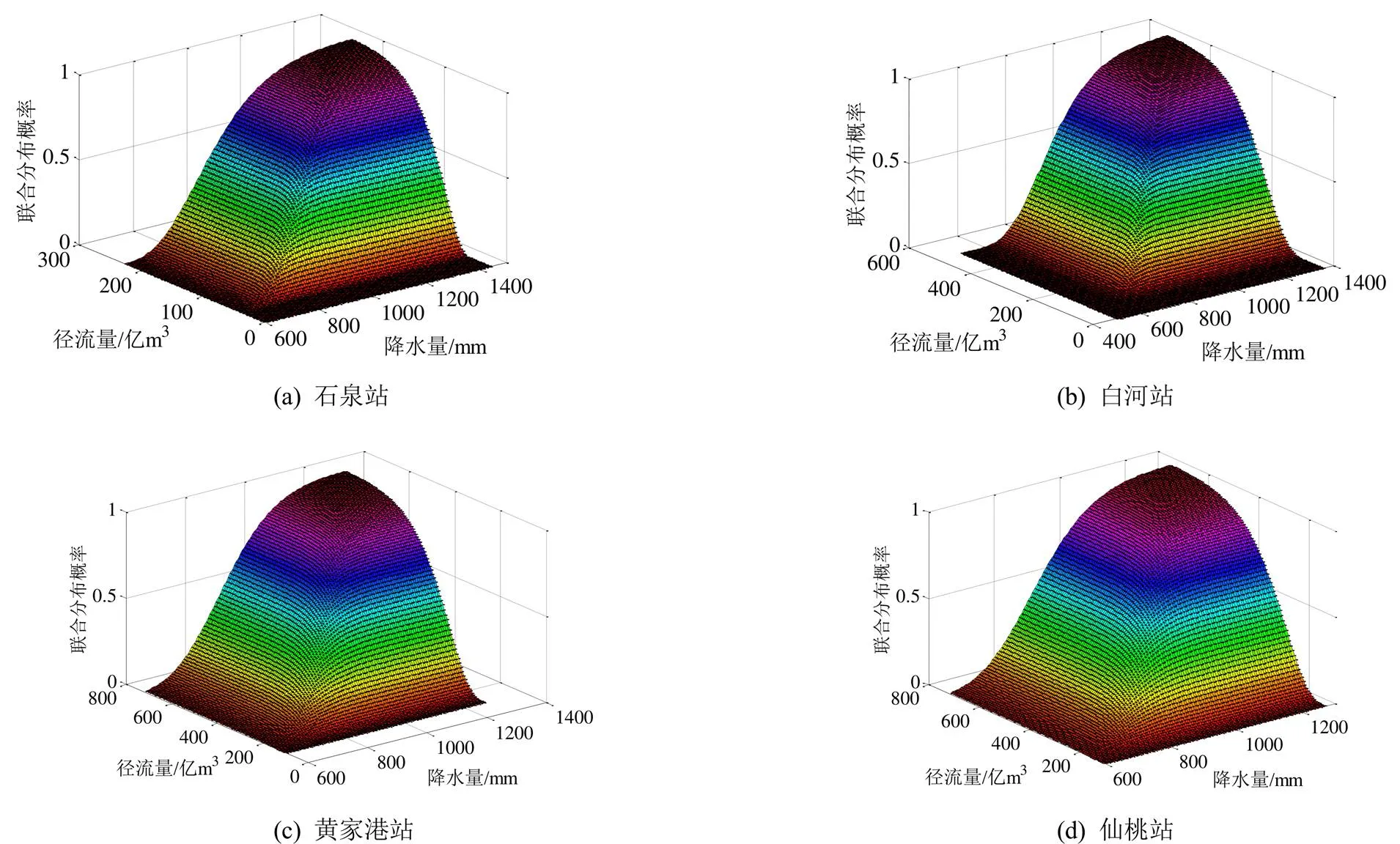
图5 各水文站径流量及控制流域降水量二维联合概率分布图

对各水文站径流量及控制流域降水量的丰枯同步概率分析可知，石泉站、白河站和黄家港站呈现出同枯＞同丰＞同平，而仙桃站呈现出同平＞同枯＞同丰；石泉站同枯概率最大，为31.80%；仙桃站同枯概率最小，为20.41%；仙桃站同平概率最大，为21.48%；黄家港站同平概率最小，为11.02%；白河站同丰概率最大，为23.28%；仙桃站同丰概率最小，为18.84%。对各水文站点径流量及控制流域降水量的丰枯异步分析可知，石泉站、白河站、黄家港站和仙桃站一平一枯概率均最大，分别为14.83%、15.45%、27.03%和22.71%；黄家港站和仙桃站一丰一平的概率相对较大，分别为15.32%和14.92%；石泉站和白河站一丰一平的概率相对较小，分别为11.94%和10.94%；黄家港站和仙桃站一丰一枯的概率相对较大，分别为2.86%和1.64%；石泉站和白河站一丰一枯的概率较小，分别为0.17%和0.16%。可见，汉江流域中下游水文站径流量及控制流域降水量丰枯异步的概率大于上游。

表5 各水文站径流量及控制流域降水量丰枯遭遇风险概率

2.3.2 各水文站径流量或控制流域降水量间的丰枯遭遇风险概率

基于优选的Copula函数建立各水文站径流量或控制流域降水量间的三维联合分布模型，得到各水文站径流量或控制流域降水量间的联合分布概率（≤,≤,≤）如图6所示，其丰枯遭遇风险概率如表6和表7所示。根据各水文站控制流域降水量间的丰枯遭遇风险概率（表6）可知，站点组合I丰枯同步概率较大，为72.88%；丰枯异步概率相对较小，为27.12%；站点组合II、III、IV的丰枯同步和丰枯异步概率均相差不大，丰枯同步概率分别为60.29%、60.15%和60.92%，丰枯异步概率分别为39.71%、39.85%和39.08%，说明4种水文站组合控制流域的降水量具有相对较好的一致性。在丰枯同步中，4种水文站组合的丰枯同步概率呈现出同平＞同枯＞同丰，站点组合I同丰、同平和同枯的概率最大，分别为17.17%、31.91%和23.80%；站点组合III同丰的概率最小，为13.43%；站点组合II同平的概率最小，为26.63%；站点组合IV同枯的概率最小，为18.76%。在丰枯异步中，4种水文站组合的一平二枯概率最大，其次为一丰二平、二丰一平和二平一枯，一丰一平一枯、一丰二枯和二丰一枯的概率最小；站点组合I一丰二平、二丰一平、一平二枯和二平一枯的概率最小，分别为4.07%、5.78%、11.38%和5.54%；站点组合II一丰二平和二丰一平的概率最大，分别为6.77%和9.06%；站点组合III一平二枯的概率最大，为16.78%；站点组合IV二平一枯的概率最大，为9.88%。

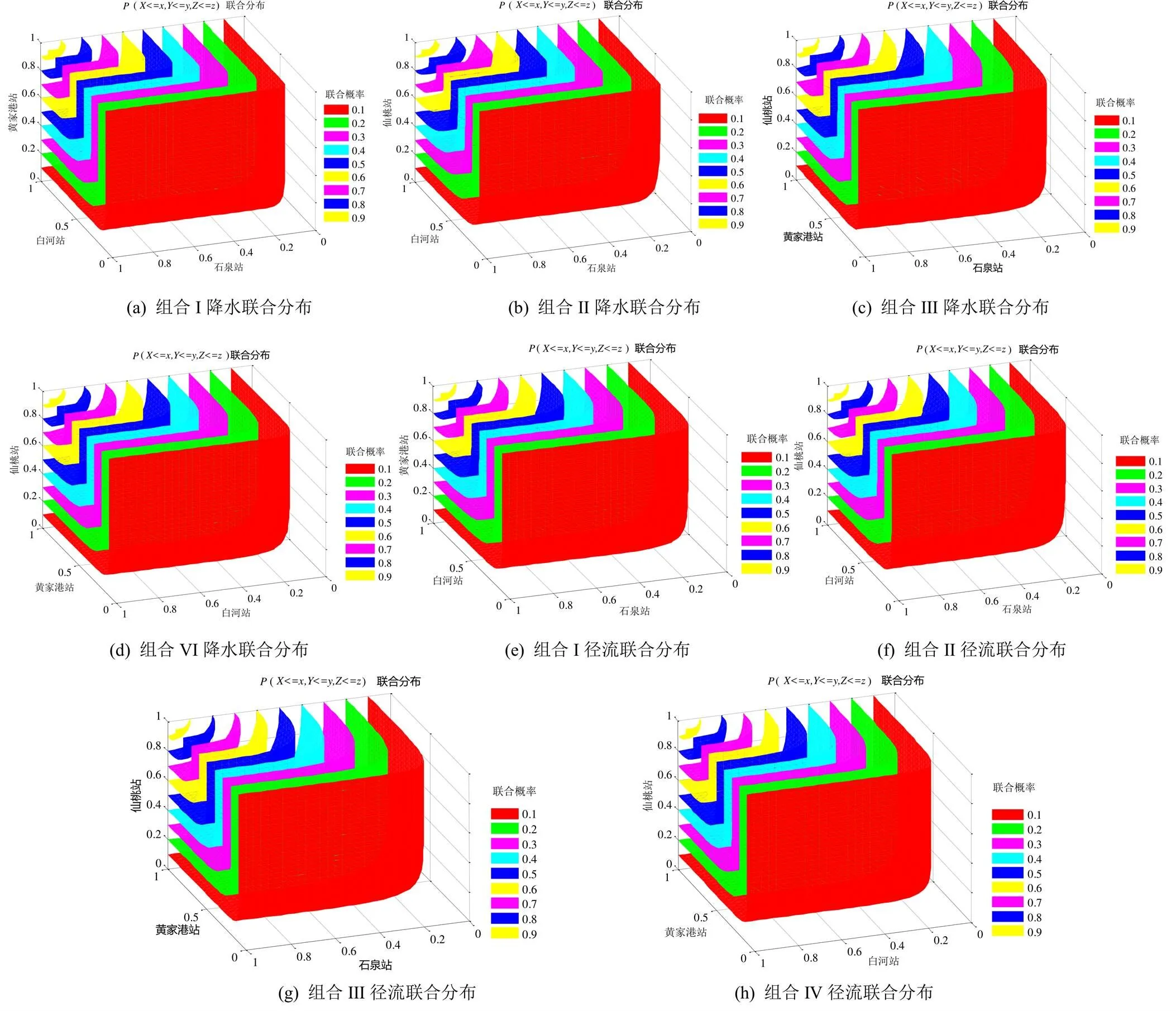
图6 各水文站径流量或其控制流域降水量间三维联合概率分布图

根据各水文站径流量间的丰枯遭遇风险概率（表7）可知，站点组合I、II、III、IV丰枯同步概率分别为59.72%、53.46%、52.82%和59.73%，丰枯异步概率分别为40.28%、46.54%、47.18%和40.27%，可见4种水文站组合下径流量丰枯同步和丰枯异步的概率接近，且丰枯同步的概率稍高。在丰枯同步中，4种水文站组合丰枯同步概率呈现出同枯＞同丰＞同平，站点组合IV同丰的概率最大，为21.95%；站点组合II同丰的概率最小，为18.41%，且同平的概率最大为5.07%；站点组合Ⅰ同平的概率最小，为3.14%，且同枯的概率最大为35.13%；站点组合II同枯的概率最小，为29.98%。在丰枯异步中，4种水文站组合下一平二枯的概率最大，其次为一丰二平、二丰一平、二平一枯和一丰一平一枯，而一丰二枯和二丰一枯的概率最小；站点组合I一丰一平一枯的概率最大，为4.09%；一丰二平、二丰一平、一平二枯和二平一枯的概率最小，分别为6.07%、8.00%、13.13%和5.93%。站点组合II一丰二平和二丰一平的概率最大，分别为7.41%和10.06%；站点组合III一平二枯和二平一枯的概率最大，分别为15.75%和7.68%；站点组合IV径流量一丰一平一枯的概率最小，为2.83%。

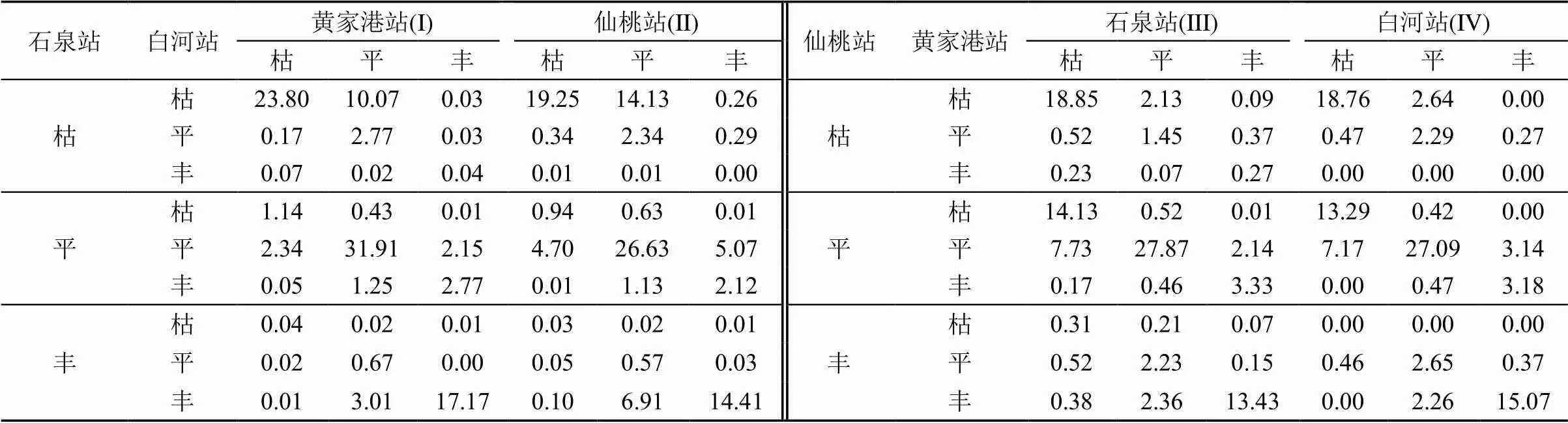
表6 各水文站控制流域降水量间的丰枯遭遇风险概率

表7 各水文站径流量间的丰枯遭遇风险概率

3 结论

1）汉江上游石泉站和白河站的径流量及控制流域降水量丰枯一致性较好，下游仙桃站丰枯一致性相对较好，而中游黄家港站丰枯一致性较差；汉江中游黄家港站径流量和控制流域降水量的丰枯同步、丰枯异步的概率接近且丰枯同步的概率稍高；汉江上中游石泉站、白河站和黄家港站丰枯同步概率呈现出同枯＞同丰＞同平，下游仙桃站丰枯同步概率呈现出同平＞同枯＞同丰；汉江中下游水文站径流量及控制流域降水量丰枯异步的概率大于上游。

2）汉江上中游石泉站、白河站和黄家港站控制流域降水量间的丰枯同步概率较大，为72.88%，且丰枯同步概率呈同平＞同枯＞同丰，丰枯异步概率相对较小，为27.12%。汉江流域4种水文站组合下径流量丰枯同步、丰枯异步的概率差异性不显著且4种水文站组合下径流量丰枯同步概率呈现出同枯＞同丰＞同平，其中站点组合IV的径流量同丰概率最大，为21.95%。

[1] 张正浩, 张强, 史培军. 基于Copula的东江流域丰枯遭遇及洪水频率分析[J]. 中山大学学报(自然科学版), 2016, 55(6): 10-19.

ZHANG Zhenghao, ZHANG Qiang, SHI Peijun. Copula-based flood frequency analysis with consideration of synchronous occurrence of wet/dry events in the East River basin[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(6): 10-19.

[2] 吴海鸥, 涂新军, 杜奕良, 等. 基于Copula函数的鄱阳湖水系径流丰枯遭遇多维分析[J]. 湖泊科学, 2019, 31(3): 801-813.

WU Haiou, TU Xinjun, DU Yiliang, et al. Multi-dimensional analysis of wetness-dryness encountering of streamflow based on the copula function in Lake Poyang Basin[J]. Journal of Lake Sciences, 2019, 31(3): 801-813.

[3] 冯平, 李新. 基于Copula函数的非一致性洪水峰量联合分析[J]. 水利学报, 2013, 44(10): 1 137-1 147.

FENG Ping, LI Xin. Bivariate frequency analysis of non-stationary flood time series based on copula methods[J]. Journal of Hydraulic Engineering, 2013, 44(10): 1 137-1 147.

[4] 李帆, 郑骞, 张磊. Copula熵方法及其在三变量洪水频率计算中的应用[J]. 河海大学学报(自然科学版), 2016, 44(5): 443-448.

LI Fan, ZHENG Qian, ZHANG Lei. Copula entropy method and its application to trivariate flood frequency calculation[J]. Journal of Hohai University (Natural Sciences), 2016, 44(5): 443-448.

[5] 姚曼飞, 党素珍, 孟美丽, 等. 基于Copula函数的泾河流域水沙丰枯遭遇频率分析[J]. 水土保持研究, 2019, 26(1): 192-196, 202.

YAO Manfei, DANG Suzhen, MENG Meili, et al. Copula-Based analysis of occrent probability on Rich-Scarce runoff and sediment in the Jinghe River Basin[J]. Research of Soil and Water Conservation, 2019, 26(1): 192-196, 202.

[6] 周念清, 赵露, 沈新平. 基于Copula函数的洞庭湖流域水沙丰枯遭遇频率分析[J]. 地理科学, 2014, 34(2): 242-248.

ZHOU Nianqing, ZHAO Lu, SHEN Xinping. Copula-based probability evaluation of rich-poor runoff and sediment encounter in Dongting Lake Basin[J]. Scientia Geographica Sinica, 2014, 34(2): 242-248.

[7] 廖显薇, 高峰, 魏婷, 等. 基于Copula函数的松花江流域水文干旱频率分析[J]. 灌溉排水学报, 2021, 40(3): 134-141.

LIAO Xianwei, GAO Feng, WEI Ting, et al. Using copula method to analyze drought frequency in Songhua River Basin[J]. Journal of Irrigation and Drainage, 2021, 40(3): 134-141.

[8] 张向明, 粟晓玲, 张更喜. 基于SRI与Copula函数的黑河流域水文干旱等级划分及特征分析[J]. 灌溉排水学报, 2019, 38(5): 107-113.

ZHANG Xiangming, SU Xiaoling, ZHANG Gengxi. Classifying drought in Heihe Basin using SRI index and copula function[J]. Journal of Irrigation and Drainage, 2019, 38(5): 107-113.

[9] 钱龙霞, 张韧, 王红瑞, 等. 基于Copula函数的水资源供需风险损失模型及其应用[J]. 系统工程理论与实践, 2016, 36(2): 517-526.

QIAN Longxia, ZHANG Ren, WANG Hongrui, et al. Risk los model of water supply and water demand based on copula function and its application[J]. Systems Engineering–Theory & Practice, 2016, 36(2): 517-526.

[10] 高超, 梅亚东, 涂新军. 基于Copula函数的区域降水联合分布与特征分析[J]. 水电能源科学, 2013, 31(6): 1-5.

GAO Chao, MEI Yadong, TU Xinjun. Analysis of joint distribution and characteristics of regional rainfall based on copula function[J]. Water Resources and Power, 2013, 31(6): 1-5.

[11] 左斌斌, 徐宗学, 叶陈雷, 等. 基于Copula函数的北京市设计降雨研究[J]. 水力发电学报, 2021, 40(2): 77-88.

ZUO Binbin, XU Zongxue, YE Chenlei, et al. Study on design rainfalls in Beijing based on copula functions[J]. Journal of Hydroelectric Engineering, 2021, 40(2): 77-88.

[12] 张翔, 冉啟香, 夏军, 等. 基于Copula函数的水量水质联合分布函数[J]. 水利学报, 2011, 42(4): 483-489.

ZHANG Xiang, RAN Qixiang, XIA Jun, et al. Jointed distribution function of water quality and water quantity based on copula[J]. Journal of Hydraulic Engineering, 2011, 42(4): 483-489.

[13] 史黎翔, 宋松柏. 基于Copula函数的两变量洪水重现期与设计值计算研究[J]. 水力发电学报, 2015, 34(10): 27-34.

SHI Lixiang, SONG Songbai. Calculation of return periods and design values of bivariate floods based on copula function[J]. Journal of Hydroelectric Engineering, 2015, 34(10): 27-34.

[14] 刘章君, 许新发, 成静清, 等. 基于Copula函数的大坝洪水漫顶风险率计算[J]. 水力发电学报, 2019, 38(3): 75-82.

LIU Zhangjun, XU Xinfa, CHENG Jingqing, et al. Estimation of dam overtopping risk rate based on copula functions[J]. Journal of Hydroelectric Engineering, 2019, 38(3): 75-82.

[15] 李胜朋, 冯剑丰, 王洪礼. 基于Copula的海洋生态系统的稳态转换[J]. 天津大学学报, 2009, 42(6): 533-538.

LI Shengpeng, FENG Jianfeng, WANG Hongli. Regime shifts of the marine ecosystem with copula[J]. Journal of Tianjin University, 2009, 42(6): 533-538.

[16] 李子远, 冯平, 苑希民. 黄河宁夏段干支流非一致性洪峰遭遇风险分析[J]. 水利水电科技进展, 2016, 36(6): 51-57.

LI Ziyuan, FENG Ping, YUAN Ximin. Coincidence risk analysis for non-stationary flood peak of Yellow River and its tributaries in Ningxia Hui Autonomous Region[J]. Advances in Science and Technology of Water Resources, 2016, 36(6): 51-57.

[17] 何英, 彭亮, 郑淑文, 等. 基于Copula函数的叶尔羌河流域洪水要素联合分布研究[J]. 中国农村水利水电, 2019(4): 74-79.

HE Ying, PENG Liang, ZHENG Shuwen, et al. Research on joint distribution of flood elements in the Yarkand River Basin based on copula function[J]. China Rural Water and Hydropower, 2019(4): 74-79.

[18] 李荣波, 黄艳, 李安强, 等. 基于Copula函数的长江大洪水随机模拟[J]. 中国防汛抗旱, 2020, 30(12): 25-28.

LI Rongbo, HUANG Yan, LI Anqiang, et al. Stochastic simulation of the Yangtze River flood based on copula function[J]. China Flood & Drought Management, 2020, 30(12):25-28.

[19] 范嘉炜, 黄锦林. 基于Copula函数的洪峰流量与洪水历时联合分布研究[J]. 中国农村水利水电, 2017(2): 204-209, 214.

FAN Jiawei, HUANG Jinlin. Combined frequency analysis of peak and duration based on copula function[J]. China Rural Water and Hydropower, 2017(2): 204-209, 214.

[20] 王深, 刘政平, 黄国和. 基于Copula方法的渭河多站点洪水风险转移模拟[J]. 水电能源科学, 2019, 37(5): 30-34.

WANG Shen, LIU Zhengping, HUANG Guohe. Copula based multivariate simulation approach for multisite flood risk transfer in Weihe River[J]. Water Resources and Power, 2019, 37(7): 30-34.

[21] 谢华, 罗强, 黄介生. 基于三维copula函数的多水文区丰枯遭遇分析[J]. 水科学进展, 2012, 23(2): 186-193.

XIE Hua, LUO Qiang, HUANG Jiesheng. Synchronous asynchronous encounter analysis of multiple hydrologic regions based on 3 D copula function[J]. Advances in Water Science, 2012, 23(2): 186-193.

[22] 梁希金, 王丽萍, 张验科, 等. 基于三维Copula函数的组合洪水研究[J]. 水资源研究, 2020, 9(1): 33-41.

LIANG Xijin, WANG Liping, ZHANG Yanke, et al. Combined flood research based on three-dimensional copula function[J]. Journal of Water Resources Research, 2020, 9(1): 33-41.

[23] 陈心池, 张利平, 闪丽洁, 等. 基于Copula函数的汉江中上游流域极端降雨洪水联合分布特征[J]. 长江流域资源与环境, 2015, 24(8): 1 425-1 433.

CHEN Xinchi, ZHANG Liping, SHAN Lijie, et al. Joint distribution of the extreme rainfall and flood for the upper-middle reaches of the Hanjiang River based on Copula function[J]. Resources and Environment in the Yangtze Basin, 2015, 24(8): 1 425-1 433.

[24] 马盼盼, 白涛, 武连洲, 等. 汉江干支流径流丰枯遭遇对跨流域调水的影响[J]. 水利水电技术, 2017, 48(8): 13-17.

MA Panpan, BAI Tao, WU Lianzhou, et al. Influence from wetness-dryness encounter of runoffs from tributaries and main stream of Hanjiang River on interbasin water transfer[J]. Water Resources and Hydropower Engineering, 2017, 48(8): 13-17.

[25] 汪成博, 李双双, 延军平, 等. 1970—2015年汉江流域多尺度极端降水时空变化特征[J]. 自然资源学报, 2019, 34(6): 1 209-1 222.

WANG Chengbo, LI Shuangshuang, YAN Junping, et al. Spatiotemporal variation of extreme precipitation regimes in the Hanjiang River Basin during 1970—2015[J]. Journal of Natural Resources, 2019, 34(6): 1 209-1 222.

[26] 胡庆芳, 曹士圯, 杨辉斌, 等. 汉江流域安康站日径流预测的LSTM模型初步研究[J]. 地理科学进展, 2020, 39(4): 636-642.

HU Qingfang, CAO Shiyi, YANG Huibin, et al. Daily runoff predication using LSTM at the Ankang Station, Hanjing River[J]. Progress in Geography, 2020, 39(4): 636-642.

[27] 高艳丽, 李红波, 侯蕊. 汉江流域生态系统服务权衡与协同关系演变[J]. 长江流域资源与环境, 2020, 29(7): 1 619-1 630.

GAO Yanli, LI Hongbo, HOU Rui. Evolution analysis on trade-offs and synergies of ecosystem services in Hanjiang River Basin[J]. Resources and Environment in the Yangtze Basin, 2020, 29(7): 1 619-1 630.

[28] 鲁帆, 朱奎, 宋昕熠, 等. 基于核密度估计和Copula函数的降水径流丰枯组合概率研究[J]. 中国水利水电科学研究院学报, 2016, 14(4): 297-303.

LU Fan, ZHU Kui, SONG Xinyi, et al. Research of combined probability of rainfall-runoff based on kernel density estimation and Copula function[J]. Journal of China Institute of Water Resources and Hydropower Research, 2016, 14(4): 297-303.

[29] 徐宇程, 朱首贤, 张文静, 等. 长江大通站径流量的丰平枯水年划分探讨[J]. 长江科学院院报, 2018, 35(6): 19-23.

XU Yucheng, ZHU Shouxian, ZHANG Wenjing, et al. Classification of high/medium/low flow year of the Yangtze river according to runoff at Datong station[J]. Journal of Yangtze River Scientific Research Institute, 2018, 35(6): 19-23.

[30] ZHANG Jinping, LIN Xiaomin, GUO Bingtuo. Multivariate copula-based joint probability distribution of water supply and demand in irrigation district[J]. Water Resources Management, 2016, 30(7): 2 361-2 375.

[31] 龙瑞昊, 畅建霞, 张鸿雪, 等. 基于Copula的澜沧江流域气象干旱风险分析[J]. 北京师范大学学报(自然科学版), 2020, 56(2): 265-274.

LONG Ruihao, CHANG Jianxia, ZHANG Hongxue, et al. Risk of meteorological drought in Lancang River Basin as analyzed by Copula[J]. Journal of Beijing Normal University (Natural Science), 2020, 56(2): 265-274.

[32] 冯瑞瑞, 荣艳淑, 吴福婷. 基于Copula函数的宜昌水文干旱特征分析[J]. 水文, 2020, 40(2): 23-30.

FENG Ruirui, RONG Yanshu, WU Futing. Analysis of hydrological drought characteristics in Yichang based on copula function[J]. Journal of China Hydrology, 2020, 40(2): 23-30.

[33] 张彦, 窦明, 李桂秋. 基于Copula 函数的水体富营养化联合风险概率研究[J]. 环境科学学报, 2018, 38(10): 4 204-4 213.

ZHANG Yan, DOU Ming, LI Guiqiu. The analysis of joint risk probability of eutrophication based on copula function[J]. Acta Scientiae Circumstantiae, 2018, 38(10): 4 204-4 213.

Using Copula Model to Analyze Consecutive Wetting-drying Occurrence in Rainfall-runoff in Hanjiang Basin

WANG Feiyu1, ZHANG Yan2*, WANG Cai3, YING Qilin4, CHEN Ting5, YU Feilong3

(1.Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China; 2. Farmland Irrigation Research Institute,Chinese Academy of Agricultural Sciences, Xinxiang 453002, China; 3. Jiangsu Province Hydrology and Water Resources Investigation Bureau, Nanjing 210009, China; 4. State Grid Luyuan hydropower company, Shenyang 110170, China;5. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

【Objective】Hanjiang is the largest tributary of the Yangtze River. The purpose of this paper is to analyze the consecutive occurrence of wetting-drying in rainfall and runoff in order to improve water resource management in this basin. 【Method】The analysis was based on runoff data measured from four hydrological stations and precipitation measured from a control catchment in the basin. The joint distribution of wetting-drying for rainfall and runoff was constructed using the two- and three-dimensional Copula functions. The risk probabilities of occurrence of wetting-drying for rainfall and runoff were calculated.【Result】The probability of consecutive occurrence of wetting and drying between runoff and rainfall at Shiquan and Baihe stations in the upper reaches in the basin were higher, being 73.06% and 73.45% respectively. The probability of consecutive occurence of wetting and drying at Huangjiagang station in the middle reaches of basins was the highest, reaching 45.21%. The probabilities of consecutive occurrence of wetting and drying at Shiquan, Baihe and Huangjiagang stations in the upper and middle reaches of basin was ranked in the order of dryness > synchronous wetness > synchronous normal, while at Xiantao station in the lower reaches, the synchronous wetness-dryness probability showed the synchronous normal > synchronous dryness > synchronous wetness. The synchronous wetness-dryness probabilities of rainfall in the control catchment for the combination of Shiquan, Baihe and Huangjiagang stations in the upper and middle reaches of the HRB were higher, 72.88%; the synchronous wetness-dryness probabilities of rainfall in the control catchment under different combinations of stations showed the synchronous normal > synchronous dryness > synchronous wetness, and that of runoff showed the synchronous dryness > synchronous wetness > synchronous normal.【Conclusion】The consistency of wetness and dryness for runoff and rainfall in the upper and lower reaches of the basin was good and fairly good, and is poor in the middle reaches. The wetness-dryness of rainfall in the control catchment under different stations has relatively good consistency, while the difference between the synchronous and asynchronous wetness-dryness probabilities of runoff was not significant.

Hanjiang River Basin; Copula function; rainfall and runoff; wetness-dryness encountering; risk probability

王飞宇, 张彦, 王偲, 等. 基于Copula函数的汉江流域降水径流丰枯遭遇研究[J]. 灌溉排水学报, 2022, 41(8): 95-105.

WANG Feiyu, ZHANG Yan, WANG Cai, et al. Using Copula Model to Analyze Consecutive Wetting-drying Occurrence in Rainfall-runoff in Hanjiang Basin[J]. Journal of Irrigation and Drainage, 2022, 41(8): 95-105.

1672 - 3317（2022）08 - 0095 - 11

P333

A

10.13522/j.cnki.ggps.2021546

2021-11-05

美丽中国生态文明建设科技工程专项资助项目（XDA23040304）；河南省自然科学基金项目（212300410310）；河南省科技攻关项目（212102311144）；中央级公益性科研院所基本科研业务费专项项目（FIRI2022-01）

王飞宇（1992-），女。博士，主要从事流域水循环模拟研究。E-mail: wangfy.14s@igsnrr.ac.cn

张彦（1989-），男。助理研究员，主要从事水资源与水环境研究。E-mail: zhangyan09@caas.cn

责任编辑：赵宇龙