基于二阶圆锥规划的大规模电动汽车充电调度优化研究＊

任 飞，田晨璐,2，张桂青,2，阎 俏,2，刘业春

(1.山东建筑大学信息与电气工程学院，山东 济南 250101；2.山东省智能建筑技术重点实验室)

0 引言

近年来，为了减少碳排放，电动汽车得到大规模的推广。预计到2030 年，电动汽车每年将消耗2710亿千瓦时的电力，需要近500 亿美元的充电基础设施。电动汽车的快速增长将会对电网的安全性造成冲击。为了降低对电网的影响和充电所带来的费用，需要对电动汽车无序充电行为进行控制。研究表明，电动汽车的无序充电问题存在于各类建筑下的充电站。因此，采用合适的算法对充电站的大规模充电行为进行调度优化，将会降低该地区电网在充电高峰时期的压力、基础设施成本和用户所支付的充电费用。在优化过程中，需考虑多种目标函数和约束条件，构建基于多目标的充电调度优化模型，来解决多目标下的电动汽车充电调度问题。

研究表明，越来越多的研究人员开始关注电动汽车的凸优化问题。凸优化算法在模型计算时，要将原优化问题转化为凸优化问题。相比于使用智能优化算法模型而言，凸优化的最大优点是，对于大规模的优化问题，也能有效地找到最优解。将模型保持凸性，则可以保证计算结果的全局最优性。

Wu等人设计了一个基于凸规划的燃料电池车辆的能源管理优化框架，能够同时优化燃料电池组和相关电源的控制决策和参数。Hu等人提出了一种基于快速凸规划的燃料电池电动卡车在线功率分配策略，来优化燃料电池系统之间的功率分配规律。Mid-Eum等人构建了一个基于凸规划的两阶电动汽车功率控制优化框架，通过最小化电池功率的大小/波动来延长电池寿命。Reza等人使用二次规划来描述混合电动汽车的能量管理问题，并通过基于ADMM的启发式优化框架来解决该问题。

为了解决现阶段充电站存在的大规模电动汽车无序充电问题，本文提出了一种基于二阶圆锥规划的大规模电动汽车充电调度优化方法。采用基于内点解算器的二阶圆锥规划，构建多目标函数的电动汽车充电模型，引入分时电价表。在加州理工学院提供的ACN-Data数据集上验证了调度优化的结果。

1 方法介绍

1.1 二阶圆锥规划算法

本实验采用嵌入式圆锥结算器（Embedded Conic Slover，ECOS），其内点算法具有Nesterov-Todd 标度和自动对偶嵌入方式，可通过对称不定KKT 系统找到搜索方向，允许具有固定旋转顺序的稳定因式分解。标准的二阶圆锥规划问题为：

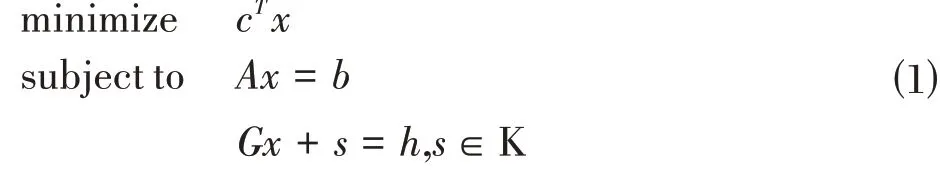
其中，是原始变量，是松弛变量，∈R，∈R ，∈R，∈R ，∈R是问题数据，K是圆锥。

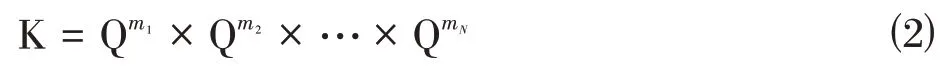
其中，

在二阶圆锥规划问题中，内点法广泛应用，其中障碍函数定义为：

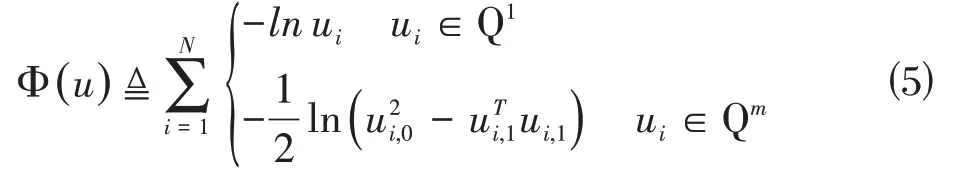
用K将约束优化问题⑴和⑷替换为一系列光滑凸无约束问题，每个问题用牛顿法一步近似求解。由此产生了一个序列：

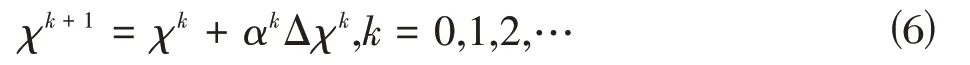
1.2 自适应充电网络

本文采用ACN-Sim仿真环境用于测试充电模型中所运用的算法。ACN-Sim 提供了一个模块化的、可扩展的体系结构，该体系结构针对实际充电系统的复杂性进行建模，其中还包括提供真实模拟场景的电动汽车充电会话开放数据集ACN-Data和充电算法现场测试框架ACN-Live，如图1所示。

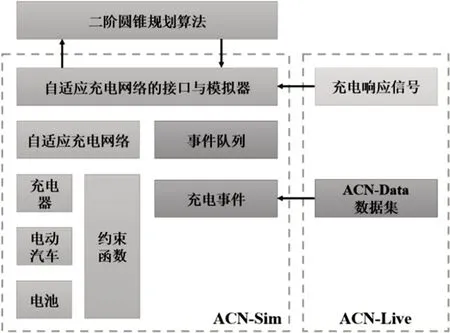
图1 自适应充电网络模拟器结构图

2 电动汽车充电调度优化模型构建

2.1 数据集介绍

本文采用的数据集ACN-Data，为用于电动汽车充电研究的公开数据集，用于评估新算法、了解用户行为。表1展示了数据集中的参数。

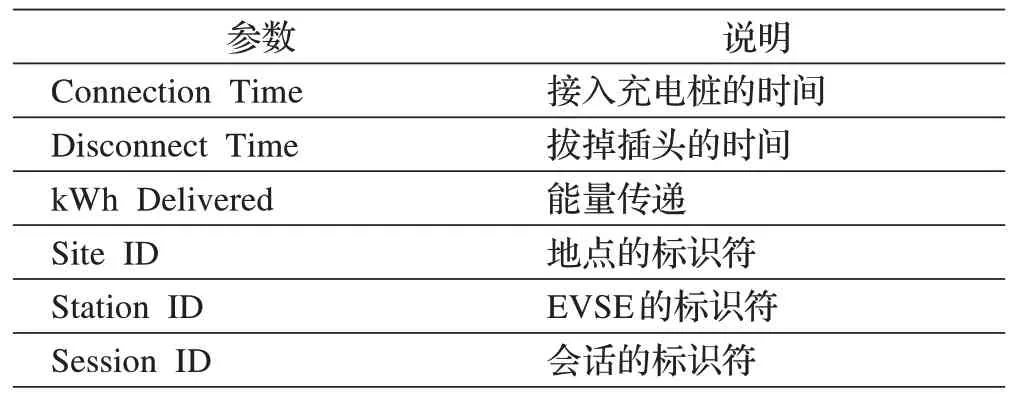
表1 ACN-Data数据集参数

2.2 电动汽车充电模型构建

在构建模型时，假设有N 辆电动汽车需要充电服务，分别使用T 和N 来表示集合T:={1,...,T} 和N:={1,...,N}，具体参数表示为：

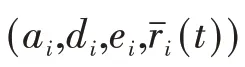
●p为分时电价；

●为即时电价；

●c是时间时的瓶颈:1,...,的可变容量；

●A是充电速率与瓶颈约束的电流相关系数；

●充电率为:=(r(),∈,∈)。

成本目标函数为：

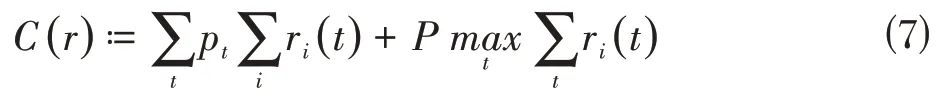
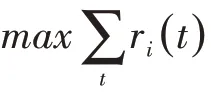
负荷峰值目标函数为：

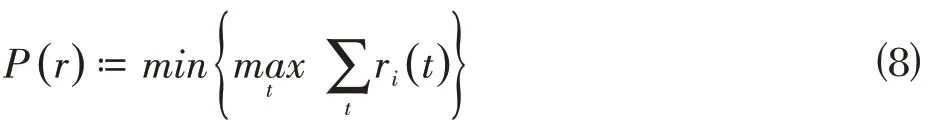
负荷波动目标函数为：

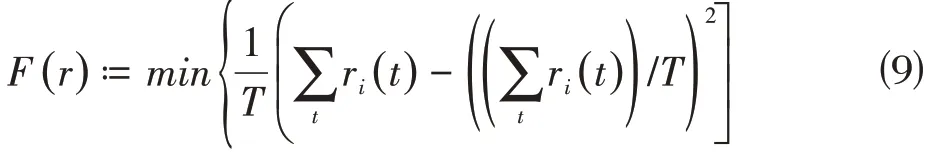
锂电池具有特定的充电特性被集成到模型中，描述在时刻的电池状态的最大充电功率：

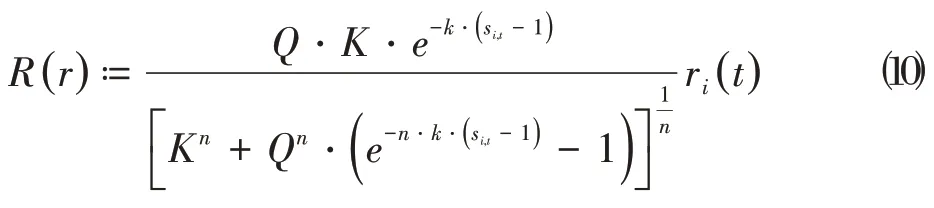
其中，,,和利用标度函数确定，具体的参数说明如表2所示。

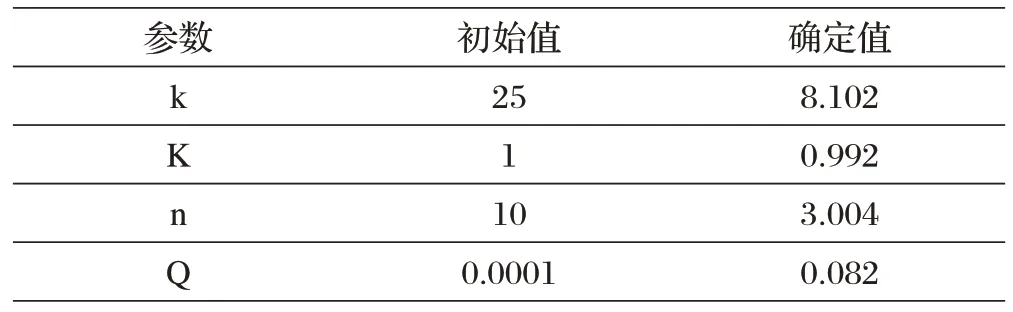
表2 建模充电曲线的参数值

约束函数定义为：

2.3 基于分时电价的优化结果验证

本文采用了Southern California Edison 所提供的分时电价EV TOU-4，如表3所示。

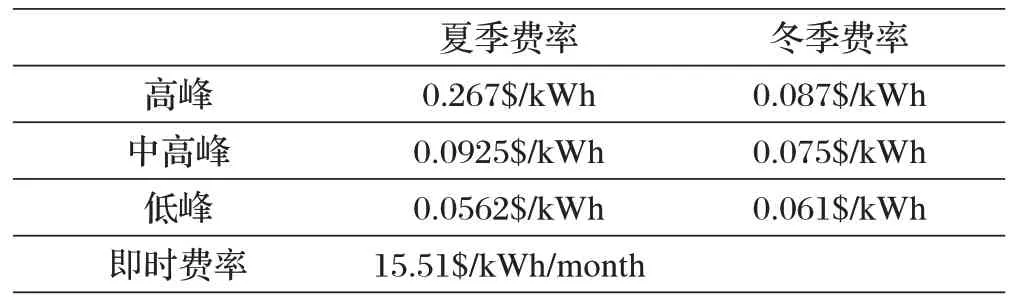
表3 分时电价表

3 实验结果与讨论

对比分时电价中存在夏冬季费率，使用不同费率下的数据来测试模型；同时对比了不同目标函数下的优化结果。其优化结果如图2、图3、图4 和图5 所示。由于存在工作日和非工作日费率，将工作日和非工作日的优化结果进行对比，如图3和图5所示。

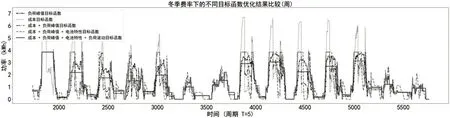
图2 冬季费率充电调度优化表（周）

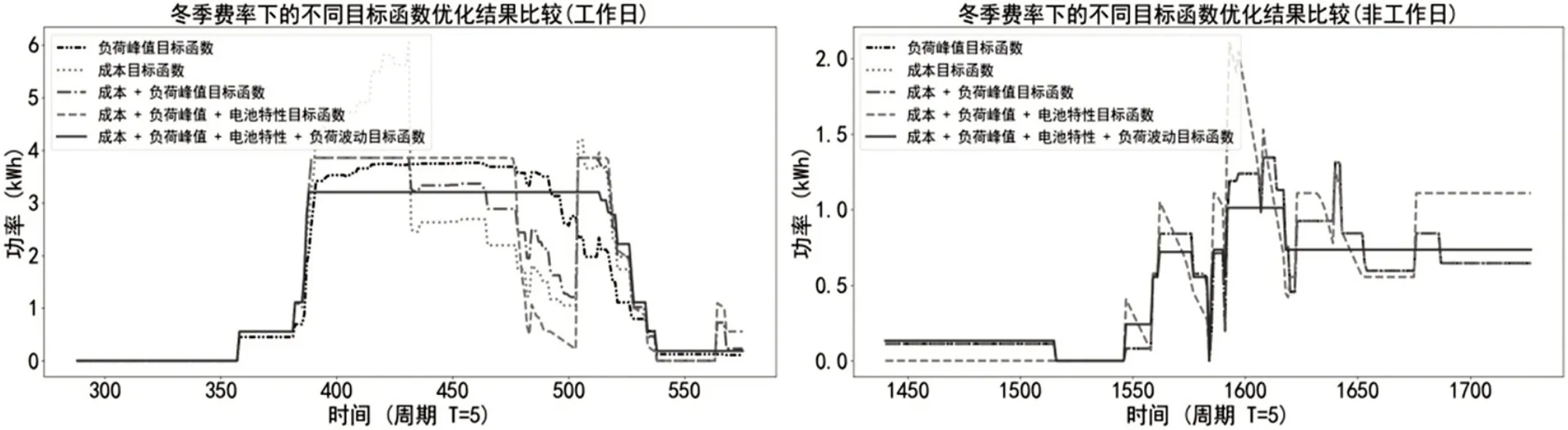
图3 冬季费充电调度优化表（工作日与非工作日）

图4 夏季费率充电调度优化表（周）

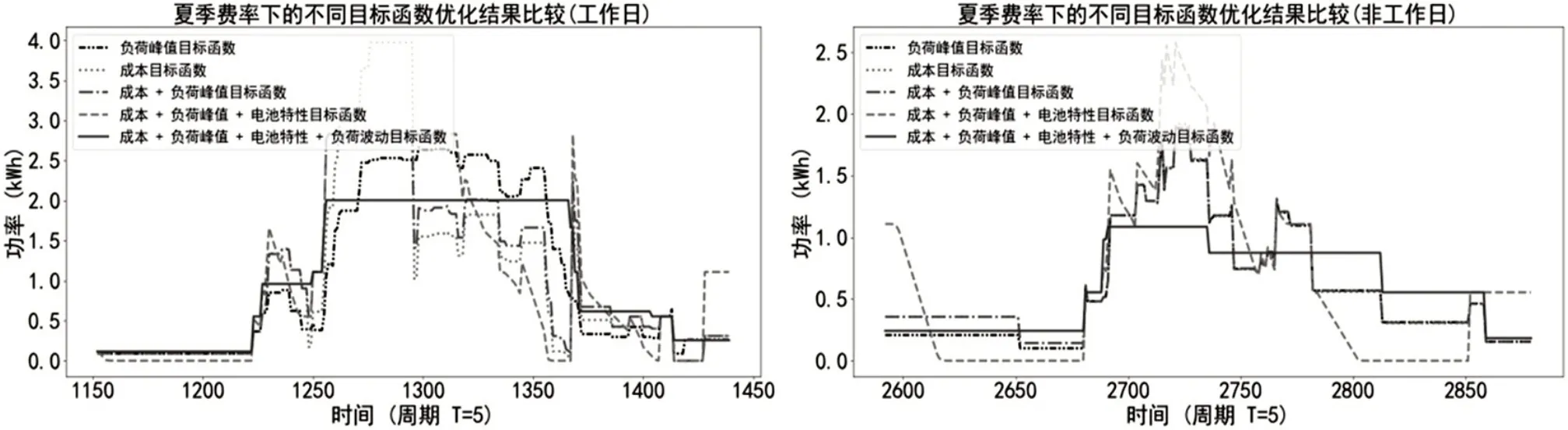
图5 夏季费率充电调度优化表（工作日与非工作日）

上述优化结果得出，以负荷峰值为目标函数时，充电峰值得到限制。以成本为目标函数时，充电过程将会在电价较低时进行。将负荷峰值与成本两目标函数相结合时，既可以限制充电负荷高峰，又可以在一定程度上减少充电费用。再添加电池特性目标函数，则优化过程会控制充电速率满足电池的充电曲线，以达到减缓电池退化的目的。当添加负荷波动目标函数时，能控制充电曲线不会出现剧烈的变化。由此可见，多目标函数的优化结果能够大幅度地降低充电时电网的峰值，缓解充电时的负荷波动程度和电池的退化问题。

表4给出了不同目标函数下的费用对比数据。

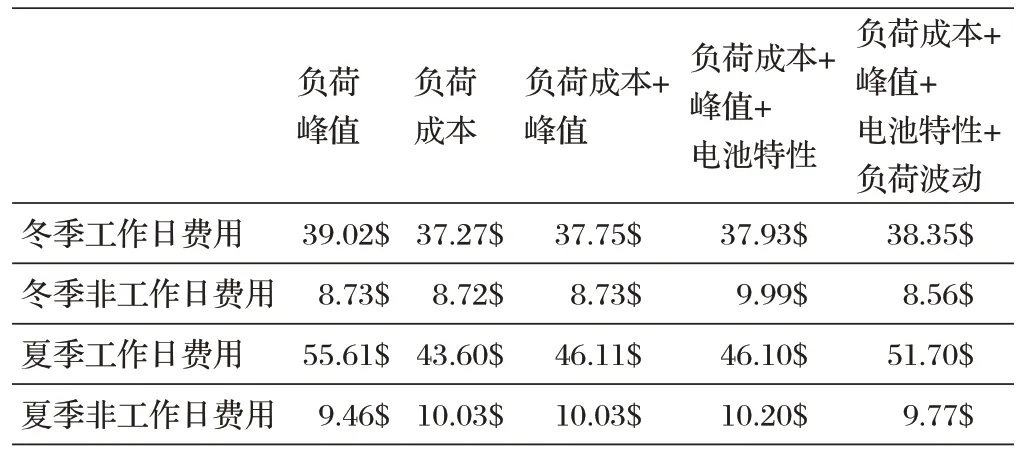
表4 不同目标函数下的费用对比

表4数据显示，采用负荷峰值目标函数时，其工作日的费用最高。在采用负荷成本目标函数时，其工作日的费用最低。当采用负荷成本+负荷峰值目标函数时，其费用处于负荷峰值与负荷成本费用之间，同时降低了成本和负荷峰值。当采用负荷成本+负荷峰值+电池特性目标函数时其费用变化不大，但是由于添加了电池特性，可缓解电池的退化问题。最后，在三目标函数的基础上添加负荷波动，采用多目标函数的模型在所需费用上相比于三目标的模型，有一定的增加，但是在考虑不同的充电问题时，仍然可以作为有效的方案。

4 结束语

在本文中，我们提出了一种基于二阶圆锥规划的大规模电动汽车充电调度优化策略，以此来指导充电站的电动汽车进行充电，使用ACN-Data 数据，证明所提出的优化调度模型能够较好地逼近最优调度结果。综上所述，该优化策略能够缓解该地区电网在充电高峰期间的压力，降低充电站基础设施的成本和用户所支付的充电费用，以及缓解电池的退化问题。

未来，我们希望在目前非实时调度优化方案的基础上开发在线优化模型。在电动汽车到达时预测充电调度优化表，并在驾驶员选择其能源需求和出发时间时向他们提供实时反馈，激励用户为系统提供更大的灵活性。