基于遗传算法优化的ELM的空气质量预测研究

许 洋，顾海航

(1.上海理工大学机械工程学院，上海 200000；2.盐城工学院)

0 引言

在人类活动及自然过程中，如NO(氮氧化物)、SO(二氧化硫)、O(臭氧)以及PM(可吸入悬浮颗粒)等污染物质进入大气，当这些物质达到了足够的浓度且超出生物圈自净能力时。将危害人体健康和生态环境。污染防治实践表明，通过建立空气质量预报模型，提前获知可能发生的大气污染过程并采取相应控制措施，是减少大气污染，提高空气质量的有效方法之一。目前常用的空气质量预报模型为WRF-CMAQ模拟体系，该模型包括WRF和CMAQ两部分：如图1所示，WRF（Weather Research and Forecasting Model）用于为CMAQ（Community Multiscale Air Quality）提供所需的气象场数据。

图1 中尺度数值天气预报系统WRF结构

如图2 所示，CMAQ 是一种三维欧拉大气化学与传输模拟系统，其根据来自WRF的气象信息及场域内的污染排放清单，基于物理和化学反应原理模拟污染物等的变化过程，继而得到具体时间点或时间段的预报结果。但是受制于模拟的气象场以及排放清单的不确定性，以及对包括臭氧等在内的污染物生成机理的不完全明晰，WRF-CMAQ预报模型的结果并不理想。

图2 空气质量预测与评估系统CMAQ结构

由此提出二次建模方法来解决该问题：在WRFCMAQ 等一次预报模型模拟结果的基础上，结合实际检测的数据源进行再建模以提高预报的准确度。首先对某空气监测提供的长期空气质量基础数据进行预处理：对缺失数据段和大量时间缺失数据的剔除，以及通过线性插值的方式补全数据文件，对预报数据和实际检测数据做时间对齐处理。然后建立ELM 网络模型作为预测算法，并使用遗传算法对ELM 进行优化，计算最佳适应度并更新最佳个体位置，通过极限学习训练和滚动预测，得到给定监测点未来三天的空气污染物浓度最优预测结果。

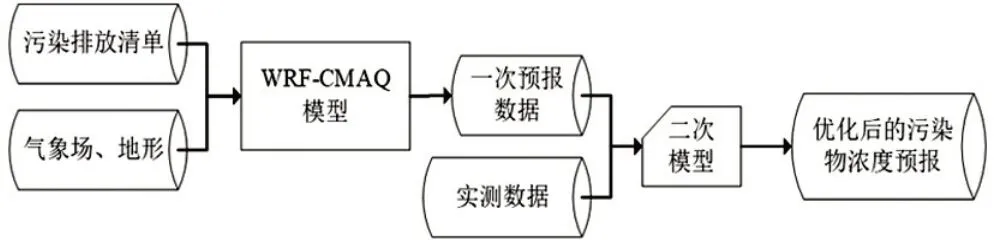
图3 空气质量预测二次建模思路

1 问题分析

本文思路框架如图4 所示：在开展建模工作之前需要对已有的一次预测以及实际检测数据预处理，以满足后期模型求解时数据输入的要求。其次需要建立一个同时适用于若干监测点的空气质量二次预报数学模型，预测未来三天数种常规污染物单日浓度值，步骤如下：①选择合适的算法并对算法进行初步调研；②利用算法建立模型；③预测结果。

图4 本文整体思路框架

2 算法选择以及算法原理

数学模型的实现可以通过单层前馈神经网络、支持向量机、BP 算法、极限学习机神经网络等算法。其中极限学习机神经网络将随机产生输入层和隐含层间的连接权值和隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层的神经元的个数，便可以获得唯一最优解，具有学习速度快、泛化能力和全局搜索能力强的优势。因此采用极限学习神经网络算法进行模型预测。

极限学习神经网络原理如下：

选择n 个不同训练样本，其中训练样本特征向量为x=[x,x,...,x]，不同训练样本对应的标签为y=[y,y,...,y]，有L 个隐藏层节点的激活函数为g(x)的ELM 的数学表达如式⑴。在针对式(1)的N 个方程简化合并后可表示为式⑵。

对ELM的网络训练等价于如下优化问题：

当g(x)无限可微时，随机给定参数Wi 和bi,ELM模型训练过程可以近似的看作求解线性Hβ=T 关于的最小二乘解，见式⑶。

输入权值矩阵和隐含层神经元的阈值是在ELM模型中随机生成，可以直接计算得出网络输出值同时迅速得到输入层权值最优解。

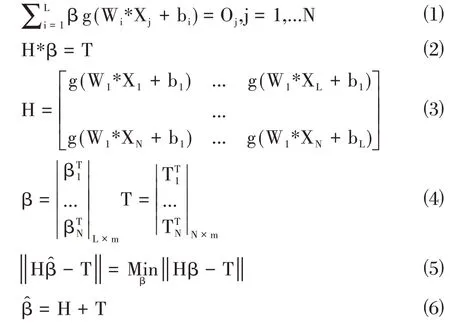
注：W为输入权重；β为输出的权重；b是第i个隐层单元的偏置；W*X表示W和X的内积；H 表示隐层输出矩阵；β表示权重矩阵；T表示期望输出矩阵。

3 处理过程

数据预处理流程如图5 所示，选择离预测日期比较近的二十四小时的数据进行处理，首先获得连续按1小时划分的预报结果数据。由于数据文件存在时间缺失数据及异常值数据，因此对三个监测点实际的测试数据进行插值处理和剔除处理。最后为了方便处理，对实际的测试数据和一次的预报数据做时间对齐处理。

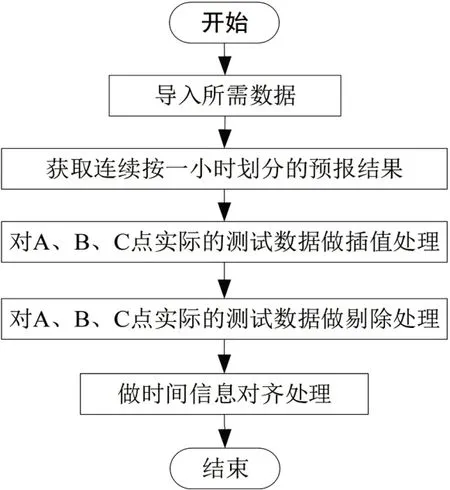
图5 数据预处理思路

3.1 数据分析

对监测站提供的监测数据文件数据，分析过程中发现数据文件存在的时间缺失数据及异常值数据。对数据中从2019/4/16 0:00:00 时-2021/7/12 23:00:00 时的时间数据进行分析，把时间统计为以1-24 时为横坐标，0:00:00-23:00:00 出现的次数为纵坐标的图形。图6为逐时实际数据小时数统计柱状图。

图6 逐时实际数据小时数统计柱状图

从图6 中可以看出，各小时的出现的实际数据不一致，例如2 时和3 时统计个数远少于800，数量误差较大，说明存在大量缺失数据。

3.2 数据插值及去除异常值处理

由数据分析步骤可以看出，存在缺失数据数据段和大量时间缺失数据，因此首先剔除缺失数据数据段，然后对数据进行插值处理，通过线性插值方法，补全数据文件，使数据成为一小时间隔的数据。污染物浓度和气象条件数据初步补全，但数据中含有部分异常值。异常数据会对使分析结果存在误差，因此在对数据进行插值处理后，采用3σ的异常值剔除原则对异常数据进行剔除，异常值处理后数据图像如图7所示。可以看出，相比于直接做插值处理的数据，去除异常值后再进行插值处理，数据变得平滑，有利于使结果更加准确。

图7 异常值处理后的污染物和气象条件数据

4 预测算法设计、优化与分析

图8 为极限学习机神经网络结构图，图中，x 为输入参数，y 为输出参数，输入参数为本预测小时之前五个时刻的气象条件和污染物浓度实际采集值，输出量为本时刻预测污染物的浓度。

图8 极限学习机神经网络结构图

ELM 算法流程大致为：首先导入数据对象，然后产生随机生产训练集和测试集，对两集做归一化处理，利用ELM 算法对其进行创建和训练，当精度或者迭代次数达到要求的时候，对结果进行仿真测试，然后进行反归一化处理，得到预测结果。

为使预测结果中AQI（空气质量指数）预报值的最大相对误差尽量小，且首要污染物预测准确度尽量高，因此要对ELM 算法进行优化。ELM 优化算法流程如图9 所示，利用遗传算法对ELM 进行优化，在建立ELM 预测模型后，通过遗传算法计算最佳适应度并更新最佳个体位置，通过极限学习训练和滚动预测，得到最优结果。

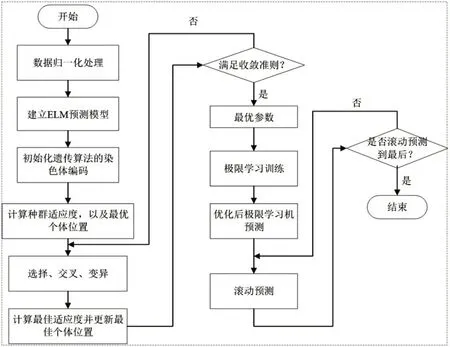
图9 ELM优化算法流程图

5 算法结果

各污染物（SO、PM2.5、O）浓度的真实值与预测值以及各污染物浓度误差值如下图10—15所示，从结果中可以看出，预测值误差均在10%范围内，同时首要污染物浓度误差最小，满足要求，结果较好。

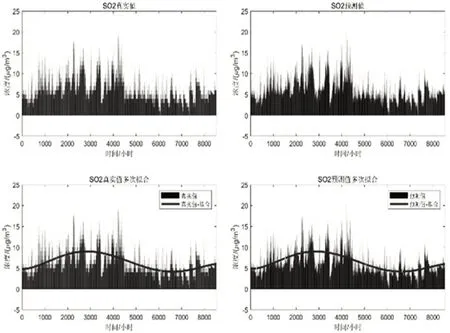
图10 SO2真实值和预测值结果及多次拟合结果

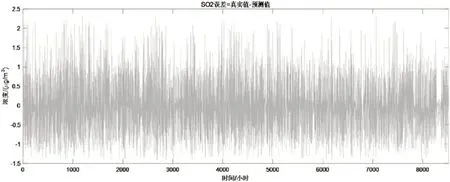
图11 SO2浓度误差计算结果

图12 PM2.5真实值和预测值结果及多次拟合结果

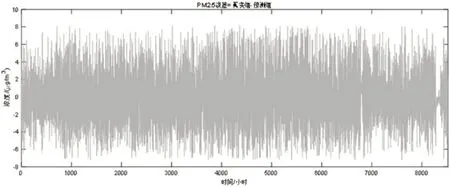
图13 PM2.5浓度误差计算结果

图14 臭氧真实值和预测结果及多次拟合结果

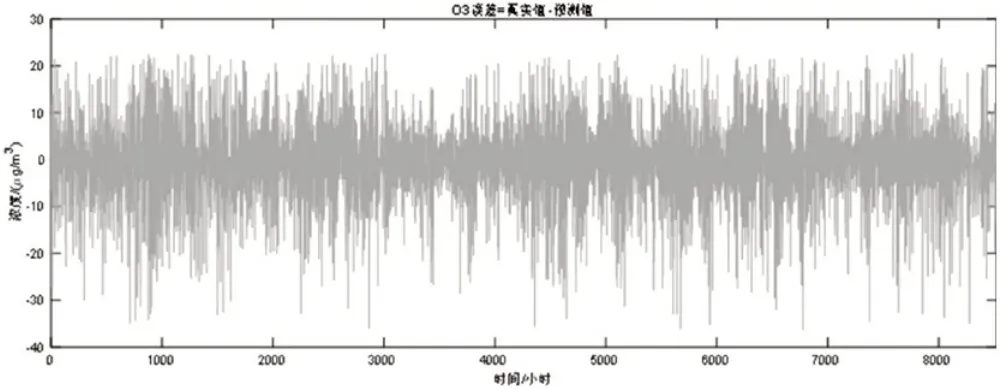
图15 臭氧浓度误差计算结果

6 结束语

本文构建的二次预报数学模型得到的预测结果准确性较目前常用的预测模型有明显提高，并对以后其他相关预报研究具有较强的现实参考意义。本文对于数据预处理使用的方法效果较好，其他相关研究中的数据均可借鉴此处理方法。但不足之处在于本模型的计算量很大且计算复杂，可根据具体情况进行优化并推广应用于其他事物的预报。