谐波齿轮传动误差主频重构与双向频谱分析

姚云鹏,陈晓霞,2+,邢静忠,2

(1.天津工业大学 机械工程学院，天津 300387；2.天津工业大学 天津市现代机电装备技术重点实验室，天津 300387)

0 引言

谐波减速器因其独特的柔性件和多齿啮合特性而具有一定的误差均衡补偿，相较于其他类型的减速器一般具有更高的传动精度。因此，在高性能精密伺服机构尤其是机器人领域得到越来越多的应用[1]。谐波齿轮在精密仪器中的应用也对其传动误差和回程误差提出了更高的要求。因此，为进一步改进传动精度提高控制质量，需要对谐波齿轮传动误差产生的来源进行分析。

谐波传动系统中的主动件一般为波发生器，因此除刚轮和柔轮的齿轮误差[2]是其传动误差的重要来源之外，波发生器也是主要贡献者。由于谐波齿轮传动比大，尽管其基频很低，但其传动误差依然表现出与波发生器转频相关的高频特性[3]。因此，对传动误差进行频域分析[4]是有效分析误差来源的方法，并在损伤分析[5]、故障诊断[6-7]和振动抑制[8-9]研究中有突出作用。

MASAFUMI等[10]在角度传达误差建模和补偿研究中将传动误差考虑为随轮齿转动的同步分量和由柔轮非线性弹性变形引起的滞后分量；JIA等[11]则将纯运动学误差分为非匀速运动分量和滞后分量；裴欣等[12]从谐波齿轮传动的误差源入手分析了传动误差产生的原因，研究了转速、载荷对谐波减速器传动误差的影响；赵琳娜等[13]建立了基于瑞利分布的传动误差多因素耦合预判模型，提出一种重新优化分配传动误差的逆向分析方法。谐波减速器传动精度的理论计算影响因素多，实际测量是误差研究的重要手段，为传动方式选择或减速器优化设计提供参考[14]。

动态误差能体现出传动系统更详细的信息，动态测量主要由测量系统高、低速轴上的光栅[15]识别。曹科等[16]利用动态齿轮传动误差原理和虚拟仪器技术，集成高精密光栅角度传感器，搭建一套测量单齿啮合和整箱传动误差的综合测量实验台；吉强等[17]研究齿轮传动误差系统信号的采集、计算和处理过程。在谐波齿轮检测方面，郝宏海等[18]利用增量式光栅传感器设计了一种谐波减速器传动精度测试仪；万筱剑等[19]针对谐波齿轮减速器的转矩、转速、效率、温升、振动和传动精度等参数进行了虚拟测试系统的研究和设计。

传动误差体现了谐波齿轮传动系统的角度传达精度，回程误差则体现了系统的重复定位精度。回程误差测试有两种方法，即使用迟滞曲线评估的静态测量法和使用双向传动误差评估的动态测量法。石照耀等[20-21]从静态和动态两个方面综合论述了精密减速器回程误差的测量原理和方法。因为迟滞曲线仅能表示出回程误差的大小而无法给出更加详细的信息，所以动态测量双向传动误差是分析和评价回程误差更有效的测量方法。

本文从谐波齿轮主要构件的运动分析其综合偏差引起的传动误差频率，构造主成分余弦波叠加的传动误差，并对各频率余弦成分及其组合特性进行分析，寻找传动误差拍频特征与各构件的关系。给出传动误差试验分析方法，分别进行一体式凸轮和滑块式凸轮两种波发生器的双向传动误差动态测试实验。通过傅里叶变换将传动误差在频域分离，验证其在理论误差频率上的响应。根据实验结果，筛选出主成分余弦进行叠加，重构传动误差曲线以验证主成分的作用。基于对比实验，验证波发生器对传动误差的影响。最后，在频域讨论双向传动误差中幅值和相位的变化，揭示回程误差产生的原因。

1 传动误差基础频率成分

谐波减速器的误差频率与其运动有关。如图1所示为谐波齿轮传动的减速运动传递示意图。当刚轮固定时，波发生器以角速度ωb输入顺时针转动，柔轮输出端产生角速度为ωt的逆时针转动。ωb与ωt的比值即为该传动系统的实时减速比。理论上减速比是常数z1/(z2-z1)，其中z1和z2分别为柔轮和刚轮的齿数。受设计、加工和装配误差的影响，实际减速比往往在某个范围内波动。

传动比的波动具体表现为输出端实际转过的角度与理想角度之间存在差异，即角度传达误差也称作传动误差。谐波齿轮传动误差具有波发生器、刚轮和柔轮3种主要来源。造成误差的主要因素包括刚轮、柔轮副的偏差和波发生器部件的偏差[3,11-12]。

1.1 波发生器来源的误差频率

源于波发生器的传动误差有两种：①由随波发生器旋转的偏差(随动偏差)，如凸轮形状的偏差，凸轮中心相对回转中心的偏心等(如图2a)引起的误差；②由不随波发生器旋转的偏差(定向偏差)，如波发生器回转中心与刚、柔轮回转中心的偏心等(如图2b)引起的误差。

图2中，椭圆代表波发生器，圆环代表柔轮，圆点代表输入轴回转中心。ωb为波发生器的角速度，则波发生器旋转频率为fwg=ωb/2π。假设刚轮和柔轮处于理想工况，双波谐波齿轮传动系统中，随动偏心e1随波发生器旋转到任意位置时，刚轮和柔轮的啮合状态均一致。因此，仅考虑随动偏心时将只产生一个常量误差[11]。仅考虑定向偏心e2时，由于波发生器结构的对称性，其在旋转180°后即开始重复，将导致传动系统出现频率为2fwg的误差。综合考虑随动偏心e1和定向偏心e2时，在波发生器完成一转时也将产生一个误差频率，即波发生器转频fwg。

由波发生器的随动偏心e1和定向偏心e2引起的误差可以通过结构设计有效消除。如图3所示为一种十字滑块式波发生器工作的示意图。图中实线圆环代表柔轮，虚线圆环代表轮毂，椭圆代表凸轮，粗实线“十”字代表十字滑块。工作时输入轴与轮毂直连，轮毂和凸轮上有滑道并通过十字滑块相连，凸轮装配于柔轮内部。o1为输入轴回转中心，o2为输出轴回转中心，o3为凸轮内孔回转中心。由图3可以看出，尽管凸轮回转中心和输出轴之间存在随动偏心e1且输入轴和输出轴之间存在定向偏心e2，但在柔轮对称约束和十字滑块两个互相垂直的滑动副的作用下，凸轮的几何中心与输出轴回转中心重合。当轮毂随输入轴转动时，在十字滑块的调节下，凸轮等同于绕其几何中心回转且与输出轴同心。此时，波发生器存在的随动偏心e1和定向偏心e2被消除了，由波发生器引起的传动误差也会被有效的减少或消除。

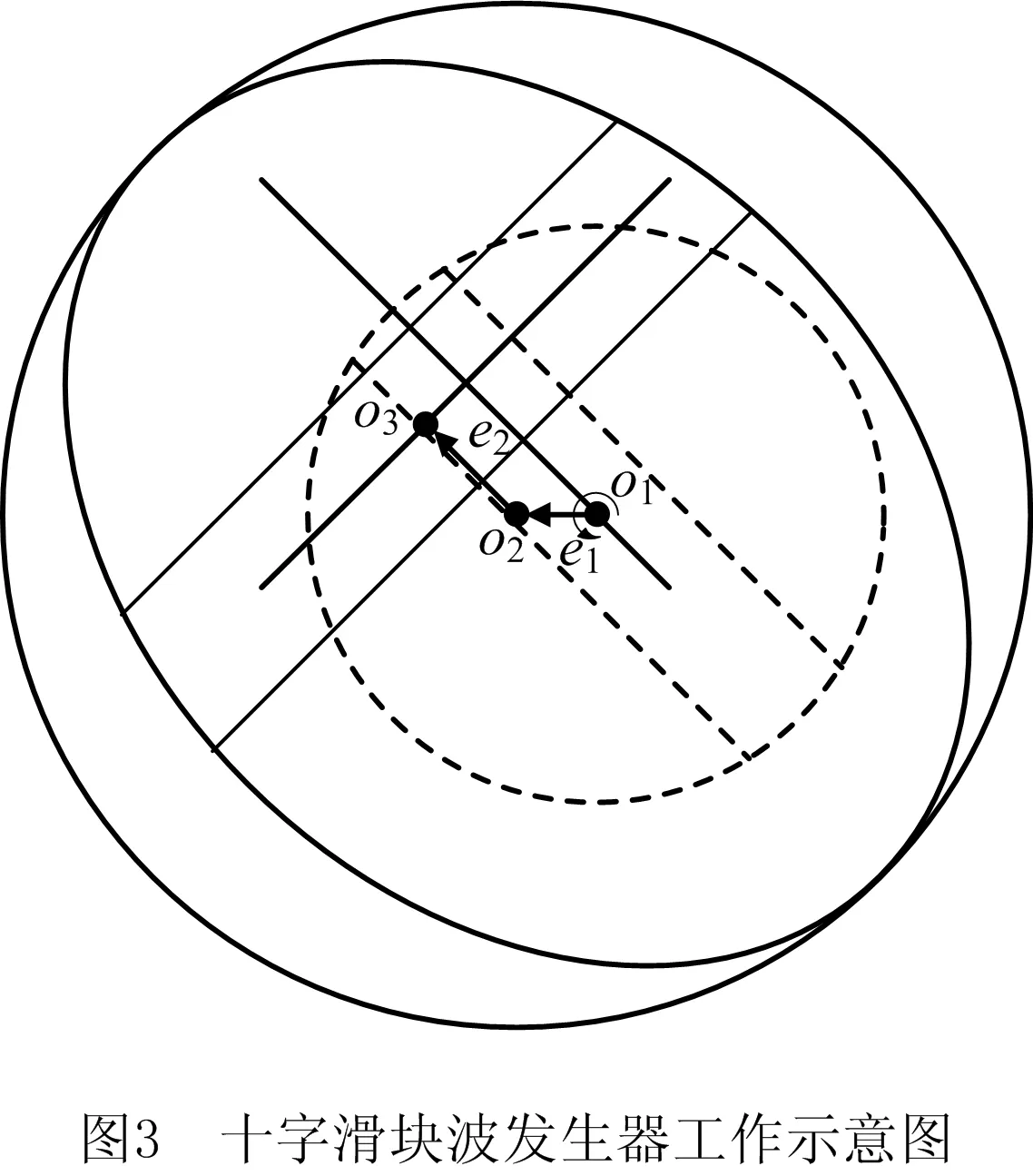
1.2 刚轮柔轮副来源的误差频率

刚轮和柔轮也存在两种误差源：①几何偏心、装配偏心和切向综合累积偏差等每周圈循环一次的综合偏差;②齿形误差等单齿距内即出现一次的偏差。对于刚轮的综合偏差，柔轮与之完成一次错齿运动则重复一次误差周期，因此在双波谐波传动中其频率为2fwg。柔轮的综合偏差影响的误差有两个频率：①与柔轮转动同频的误差，其频率为2fwg/z1；②柔轮与刚轮完成一次错齿运动则重复一次的误差频率2fwgz2/z1[3]。

齿形误差影响刚轮与柔轮的实际啮合状态，其引起的传动误差频率与齿数有关。双波谐波传动中刚轮与柔轮的齿形误差的频率均为2z2fwg。但谐波齿轮齿数大且具有多齿啮合特性，这种超高频的齿频误差忽略不计。除此之外，还有一些超高频：如由轴承滚动体误差导致误差频率k1fwg(k1为滚动体数目)、由凸轮多棱度导致的误差频率k2fwg(k2为凸轮棱数)等。通常滚动体的误差较小，凸轮的多棱度也很小，这些超高频误差也忽略不计[3]。

因此，双波谐波齿轮中误差频率的基础成分主要有：柔轮转频2fwg/z1(固定柔轮使刚轮输出时,该频率为2fwg/z2)、波发生器转频fwg、刚轮啮频2fwg和柔轮啮频2fwgz2/z1。

2 传动误差余弦重构表达及基础主频成分叠加特性

2.1 传动误差的余弦重构表达式

尽管传动误差的采集信号实际上是一段离散的有限长数组，但由前述分析可知其本质是连续的三角函数波的叠加组合。根据余弦曲线的一般表达式

C=Acos(2πft+φ)，

(1)

构造理论传动误差

(2)

式(2)表示传动误差由Q个余弦波叠加一个常量E0构成。其中Aq、fq和φq分别为余弦波Cq的幅值、频率和相位。

2.2 基础主频余弦波的叠加特性

由于波发生器的定向偏差和刚轮的综合偏差都将导致频率为2fwg的误差，相同频率不同幅值和相位的余弦波叠加后依然是此频率的余弦波。因此取Q=4，关注4个不同基础主频的误差曲线。假设波发生器转频fwg=0.5 Hz，刚轮齿数z2=162，柔轮齿数z1=160。此时Cq的频率如表1所示。不失一般性，先将余弦曲线Cq的幅值Aq都设为1″(角秒)，相位φq都设为π。此时，余弦Cq的曲线如图4所示，其局部图如图5所示。

表1 传动误差的理论基础主频成分

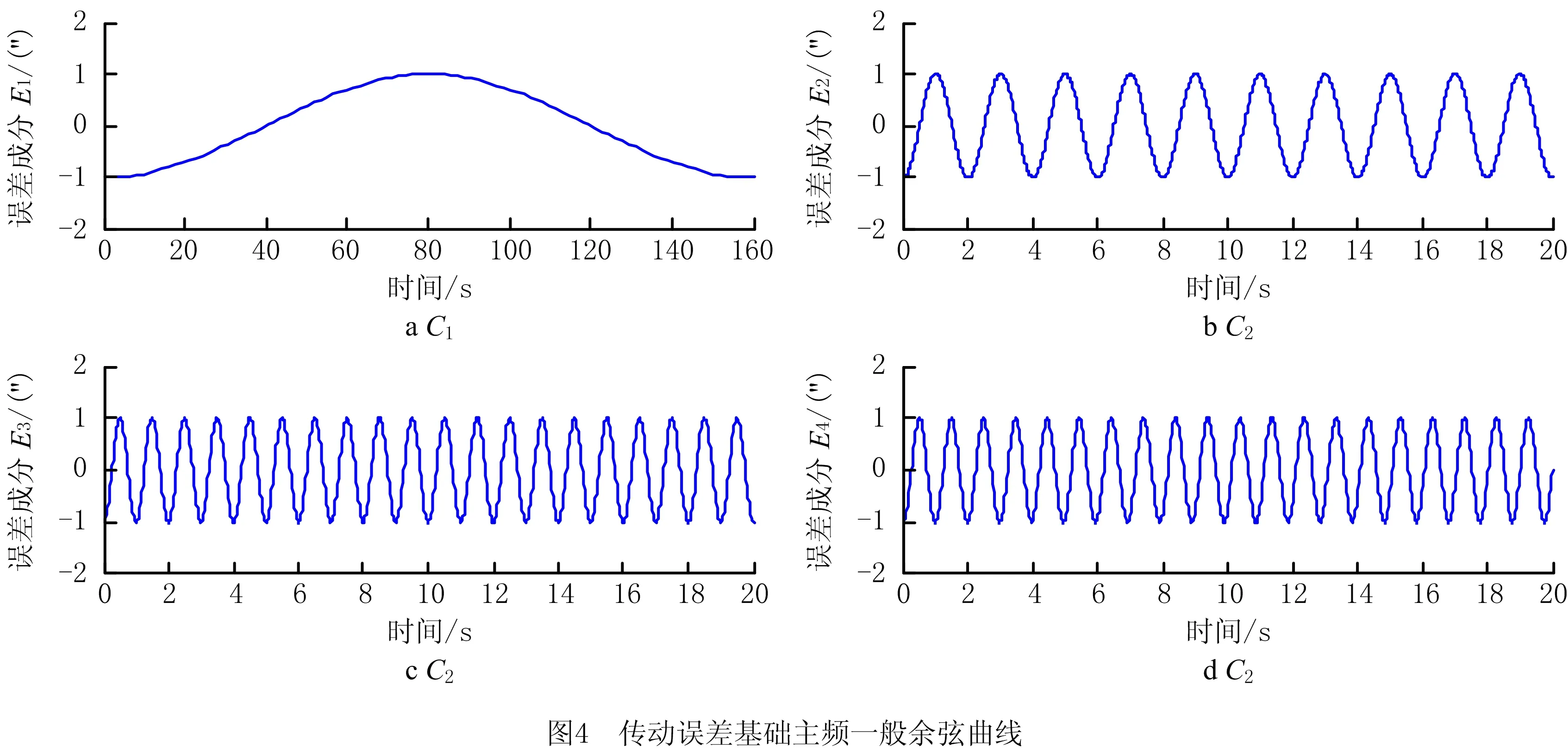
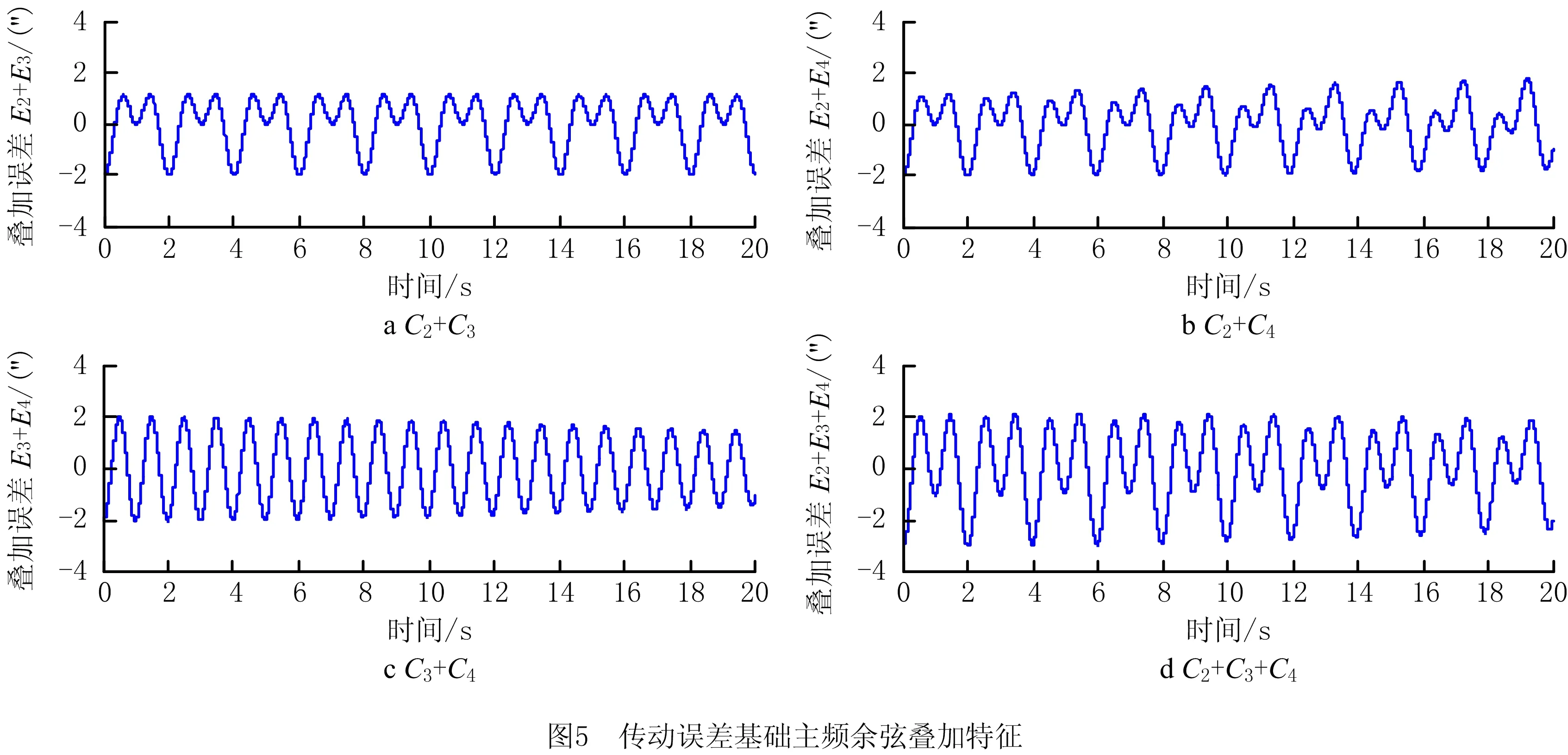
图4显示了谐波齿轮传动各理论误差频率上的简谐曲线。可以看出，C1的频率最小而周期最长，在柔轮转动一圈后完成一个周期。因此C1将影响整个传动误差的大周期特征。C3的频率是C2的两倍，C4的频率近似是C2的两倍。

由于存在倍数和近似存在倍数关系，图4中C2与C3或C4叠加将产生局部“大小波”的现象(如图5a和图5b)。C3与C4频率接近，两者叠加后的波形在有限长的局部近似呈简谐波形状(如图5c)。波发生器转频、刚轮啮频和柔轮啮频误差叠加后的综合特征如图5d所示。可见，具有二倍关系频率的误差叠加将引起“大小波”现象。

2.3 基础主频余弦波叠加的拍频现象

图5中，C2与C3频率呈倍数关系，其叠加后除“大小波”外，不具有拍频特征。而频率没有倍数关系的组合，如C2+C4、C3+C4都将产生周期性拍频现象。如图6所示为不同叠加组合下的拍频特征。宏观上看，C2+C3确实不具有拍频特征(如图6a)，C2+C4具有波浪形拍频特征(如图6b)，C3+C4则具有纺锤形拍频特征(如图6c)。可见，波发生器综合偏心与刚轮综合偏差叠加将不会产生拍频，波发生器综合偏心与柔轮综合偏差叠加将产生波浪形拍频，刚轮综合偏差与柔轮综合偏差叠加将产生纺锤形拍频。在波发生器综合偏心、刚轮综合偏差和柔轮综合偏差的综合影响下，拍频也会叠加(如图6d)。在柔轮转动一圈的周期内，拍频特征重复两次。

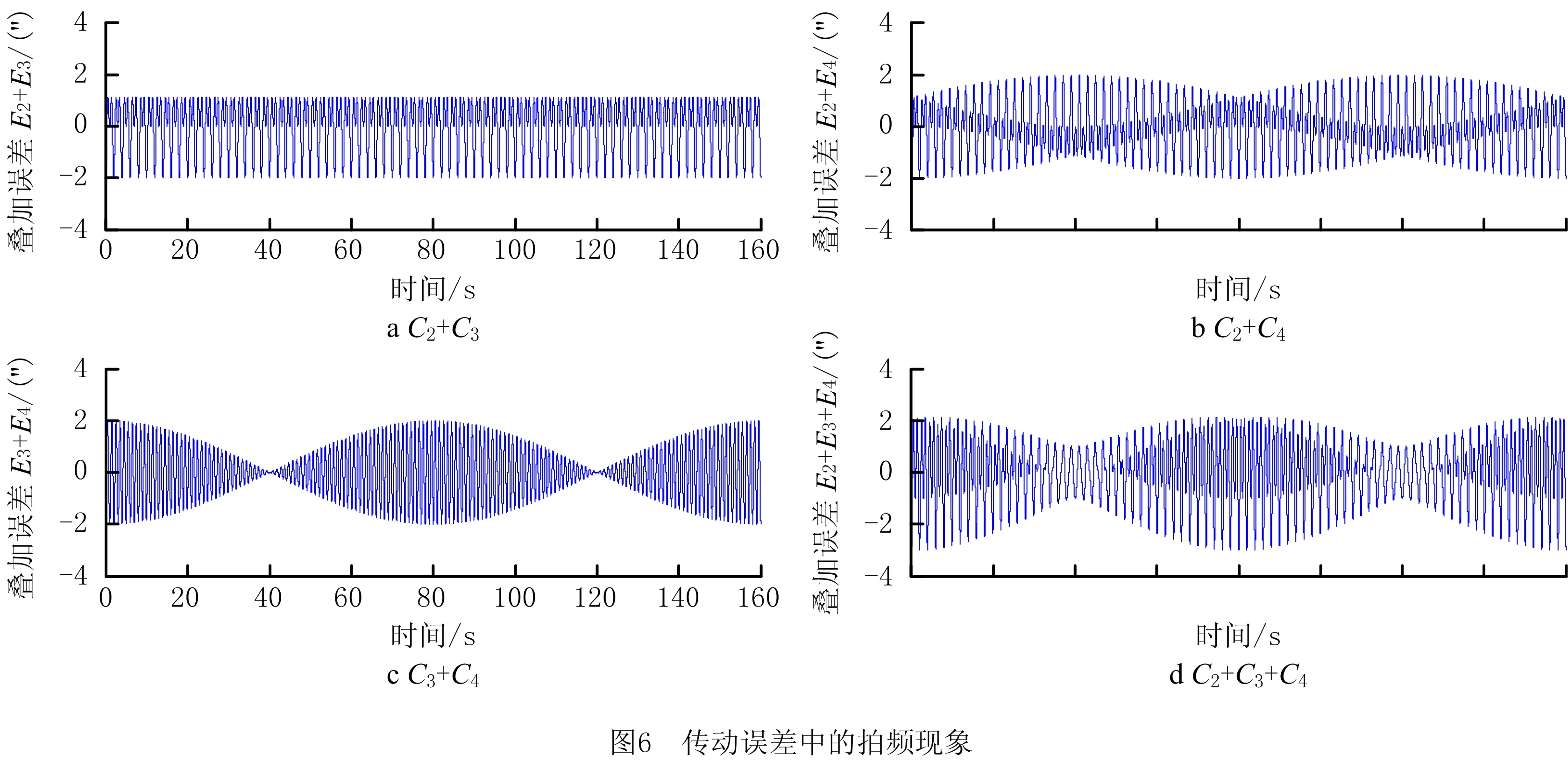
如前文所述，图4～图6中各余弦波的幅值均为1″，相位均为π，是对余弦波叠加特性的数学分析，所得结论具有一定的普适性。但实际工况下，各误差的余弦波幅值和相位都不相同，与其误差源的偏差分布有关，如波发生器、刚轮和柔轮的偏心大小与方向等。因此实际叠加结果与图5和图6上的细节有所区别，但其大小波、拍频等形貌特征是一致的。除此之外，在谐波齿轮运转过程中，基础频率成分互相影响也将叠加出更多的频率成分。例如，波发生器偏心将影响刚轮啮频误差的幅值，此时幅值由常数变为周期函数从而形成频率叠加后的信号。因此，实际传动误差的成分更多，拍频现象也更复杂。总体来说，波发生器、刚轮和柔轮的综合偏差越小，传动误差也会越小。

3 采样误差的傅里叶频域离散

为验证前述理论分析的准确性，对传动误差进行实验。实验中的采集信号是一段在时域上离散的有限长数组，它包含了所有误差影响因素的作用信息。在采集数据量足够的条件下，可利用傅里叶分析，计算在频域上等间隔分布的所有频率上的响应，响应的相关性大小由各频率的幅值和相位来评估。

设传动误差E(t)是时域上周期为T的连续曲线。它由常量a0/2和N个余弦函数叠加组成，则式(2)可扩充表达为：

(3)

式中An、n/T和φn分别为第n次余弦波的幅值、频率和初相。

将式(3)中的余弦波分解为正交的正弦分量和余弦分量。即

(4)

其中：an=Ancosφn，bn=-Ansinφn。

在t0到t0+T对式(4)进行积分，根据三角函数的正交性得a0、an、bn与传动误差E(t)的关系分别为：

(5)

3.1 误差的傅里叶变换

根据欧拉公式，式(4)中正弦分量和余弦分量可表达为：

(6)

将其代入式(4)并整理得：

(7)

由式(5)可知，a-n=an，b-n=-bn。当n=0时an=a0，bn=0。 因此，由式(7)可整理出传动误差E(t)的傅里叶级数：

(8)

令复数cn=(an-ibn)/2，结合式(5)和式(6)可得：

(9)

由于实际采集的误差信号在时域上离散无法积分，设Ek为E(t)连续曲线上等间隔采样的点数为N的误差序列，其时间特性以采样频率fs体现。在未知Ek周期的情况下，将其周期视为采样点数N。于是，基波频率

f=fs/N。

(10)

设Fn为N倍复数cn，并将式(9)以求和的方式给出，即

(11)

式中n和k均为1到N的正整数。

3.2 余弦波成分的幅值与相位

Fn对应的频率为(n-1)f，即Fn确定了n-1次余弦波。设Fn的实部为Rn，虚部为In。当n=1时，对应频率为0，此时F1=R1是实常数，即误差常量；当n>1时，Fn的模为cn的N倍，即n-1次余弦波幅值An-1的N/2倍。Fn的相位角即n-1次余弦波初相φn-1。因此，

(12)

φn-1=argFn=tan-1(In/Rn)。

(13)

由式(11)可知FN-n=F-n，它与Fn共轭，即模相等，相位相反。因此，傅里叶变换后的Fn具有负频率结果，且与正频率结果左右对称。负频率是共轭复数的数学运算结果，不具备实际物理意义[22]。将负频率与正频率幅值合并考虑才是该频率余弦波的实际贡献(如式(12))。根据式(11)，傅里叶变换能识别的最大频率为Nf/2，为采样频率fs的一半，遵循奈奎斯特采样定理。通过快速傅里叶变换方法(Fast Fourier Transform,FFT)对式(11)进行计算，然后由式(12)和式(13)即可确定各频率下的幅值响应与相位信息。

4 实验算例与分析

4.1 传动误差实验设计

采用志方ZRT-II机器人减速器性能测试系统(如图7)测试ZSHF17-80-2SO谐波减速器(如图8)。角度传感器采用HEIDENHAIN-ERA4 282C系列的圆形光栅，采集系统采用NI-R系列PCI-e7 842采集板卡。减速器主机由环形刚轮和礼帽形柔轮装配在交叉滚子轴承两端构成。刚轮和交叉滚子轴承外圈固定在台架上，实现波发生器输入、柔轮输出的传动方式。刚轮齿数z2=162，柔轮齿数z1=160，约束刚轮时其传动比为80。

波发生器采用两种方案：方案一，一体式凸轮波发生器，其中凸轮直连电机轴；方案二，滑块式凸轮波发生器，其中凸轮与直连电机的轮毂之间装配十字滑块。两个凸轮长短轴尺寸偏差均小于5 μm。设置输入轴转速n1=30 rpm，此时fwg=0.5 Hz。其主要关注频率如表1所示。采样间隔0.1s，即采样频率fs=10Hz。系统稳定运转后记录实时时间t、输入轴转速n1、输出轴转速n2、输入轴转角r1和输出轴转角r2。参考标准要求[23]对传动误差进行动态测试。在输出端转动370°后输入轴反向运转。通过输入轴转速与输出轴转速的比值计算实时传动比。实时传动误差X(j)=r1/80-r2。

4.2 双向误差测试结果

如图9a所示为方案一的传动误差测试结果。可以看出，在177.3 s反转的瞬间，传动误差曲线出现跳跃，前后两段曲线对称相似。将信号以输出端转角为轴绘制空域传动误差如图9b所示。传动误差曲线在输出端转角为360°位置改变方向。在图9b中，转角对齐的情况下对正反向传动误差曲线求差，获得空域回差曲线如图9c所示。

4.3 误差信号的频域分离

根据第3章所述方法分别对图9a所示的两段传动误差进行计算。得到在频域上表达的幅度谱(如图10a)和相位谱(如图10b)。图10a中反向幅值亦为正数，为便于观察，取负数进行显示以与正向幅值进行分开对比。

从图10a可以看出，在0 Hz、0.5 Hz、1 Hz附近出现较大的幅值，与表1数据大致对应，说明第1章的误差源分析基本准确。但图10a还显示出传动误差信号在2 Hz、3 Hz附近也有较大的相关性，这些频率是刚轮啮频的2倍频和3倍频。

由于回程误差是在正向传动误差与反向传动误差空域上作差，反向传动误差从时域转到空域时改变了延伸方向，因此对反向传动误差的时域信号的相位乘-1后进行分析。将余弦波信号的相位在频域展开，如图10b所示。关于正反向的结果对比将在第5章中进行详细讨论，这里先对反向传动误差曲线进行分析。

表2中列出了其所有响应频率中幅值大于2″的成分。与表1对比，表2中0Hz对应误差常量，0.006 22 Hz对应柔轮转频2fwg/z1，1.000 62 Hz对应刚轮啮频2fwg，1.013 05 Hz对应柔轮啮频2fwgz2/z1。波发生器输入转频fwg(0.5 Hz)处的幅值响应较小，未列于表中。0.559 35 Hz是以波发生器输入转频fwg为主导的叠加频率。除此之外，刚轮啮频的两倍频率4fwg处的响应幅值达到了4.86″，除误差常量外该幅值是所有余弦波的最大值。

表2 反向传动误差主要频率成分

4.4 传动误差余弦函数重构

结合表1给出该误差曲线理论基础主频成分余弦波参数如表3所示。分别由表2和表3中的成分根据式(2)对传动误差E(t)进行重构，该误差还包含常量E0=13.98″，结果如图11所示。

图11中，重构方案(I)为表3中基础主频成分叠加的效果，可以看出基础主频成分的误差成分组合已经能够反映出传动误差的整体趋势，但在幅值和细节上与真实传动误差还存在较大的差异。因此，重构方案(II)为表2中实际主频成分的叠加效果。可以看出，实际主频成分重构误差与原始误差基本重合，已能够反映出实际传动误差的幅值大小和大部分细节。图11结果表明，第1章和第2章中的理论分析准确，理论误差来源引起的频率确实存在。理论基础主频成分的叠加准确反映出实际传动误差的整体拍频特征，但在幅值和细节上没有反映实际传动误差的大小和形貌特征。理论基础主频频率叠加后形成的主要频率成分在构成传动误差的幅值和细节形貌特征上具有重要作用。

5 讨论

5.1 波发生器结构对传动误差的影响

滑块式凸轮波发生器通过十字滑块连接凸轮和轮毂起到了联轴节的作用，一定程度上能够调节凸轮的回转偏心和几何偏心(如图3)，进而可能对传动误差产生影响。保持主机工况和测试参数不变，更换滑块式凸轮波发生器，重新测试。如图12所示为方案二的传动误差测试结果。

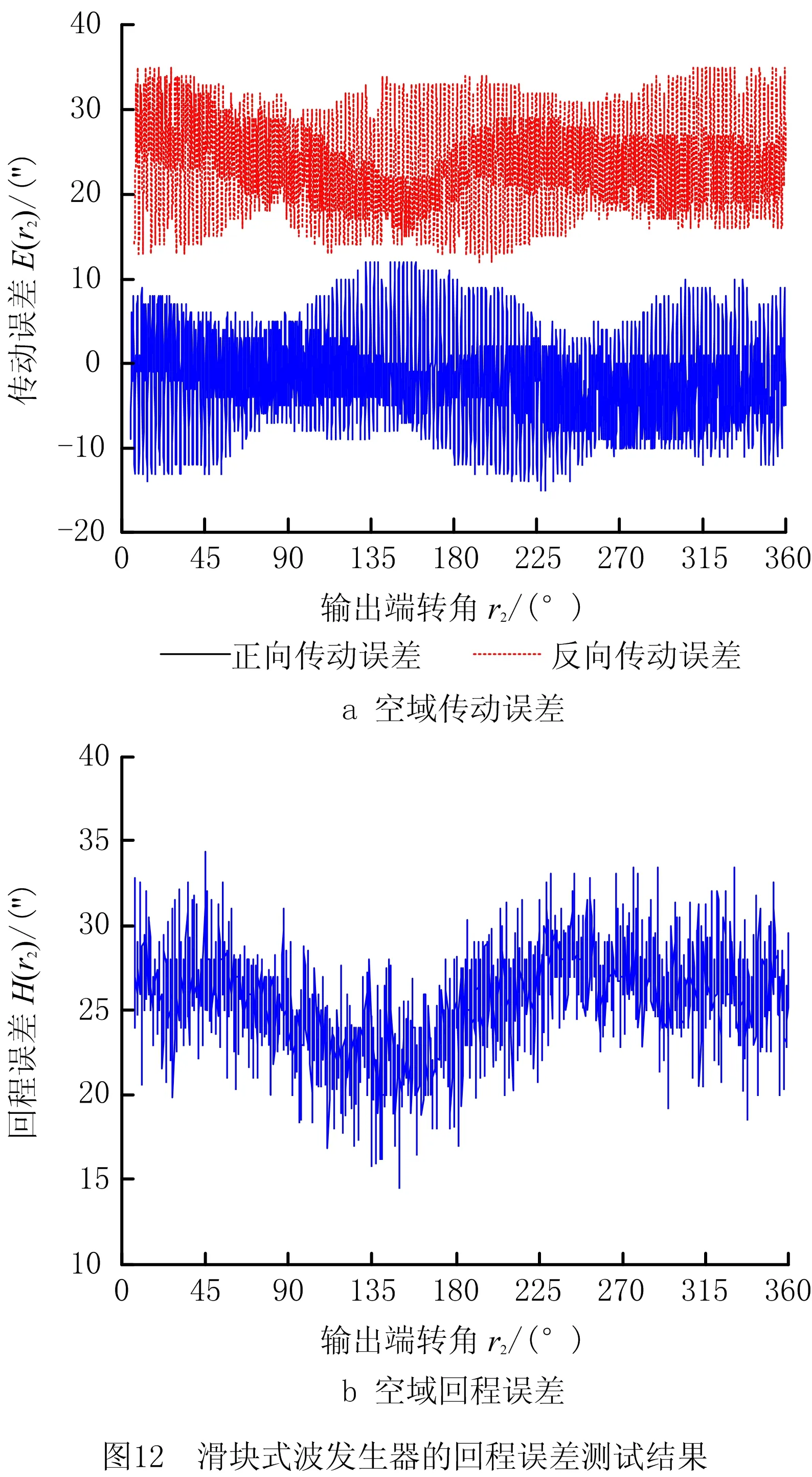
比较图12a和图9b可以看出，在滑块装配间隙的影响下正反向的传动误差曲线在空域上明显分离，且曲线形态特征显著变化。比较图12b和图9c，可以看出回程误差明显增大且形态显著变化。

如图13所示为方案二传动误差的频谱结果，其处理方法与图10一致。图13a中显示出误差在0 Hz、1 Hz、2 Hz和3 Hz位置附近拥有较大的响应，而在0.5 Hz附近没有显著响应。根据图9和图11中的测试数据，方案一与方案二的误差结果总结如表4所示。可以看出，相对于方案一，方案二中正反向传动误差分别降低了5″和10″，回程误差增大近8″。

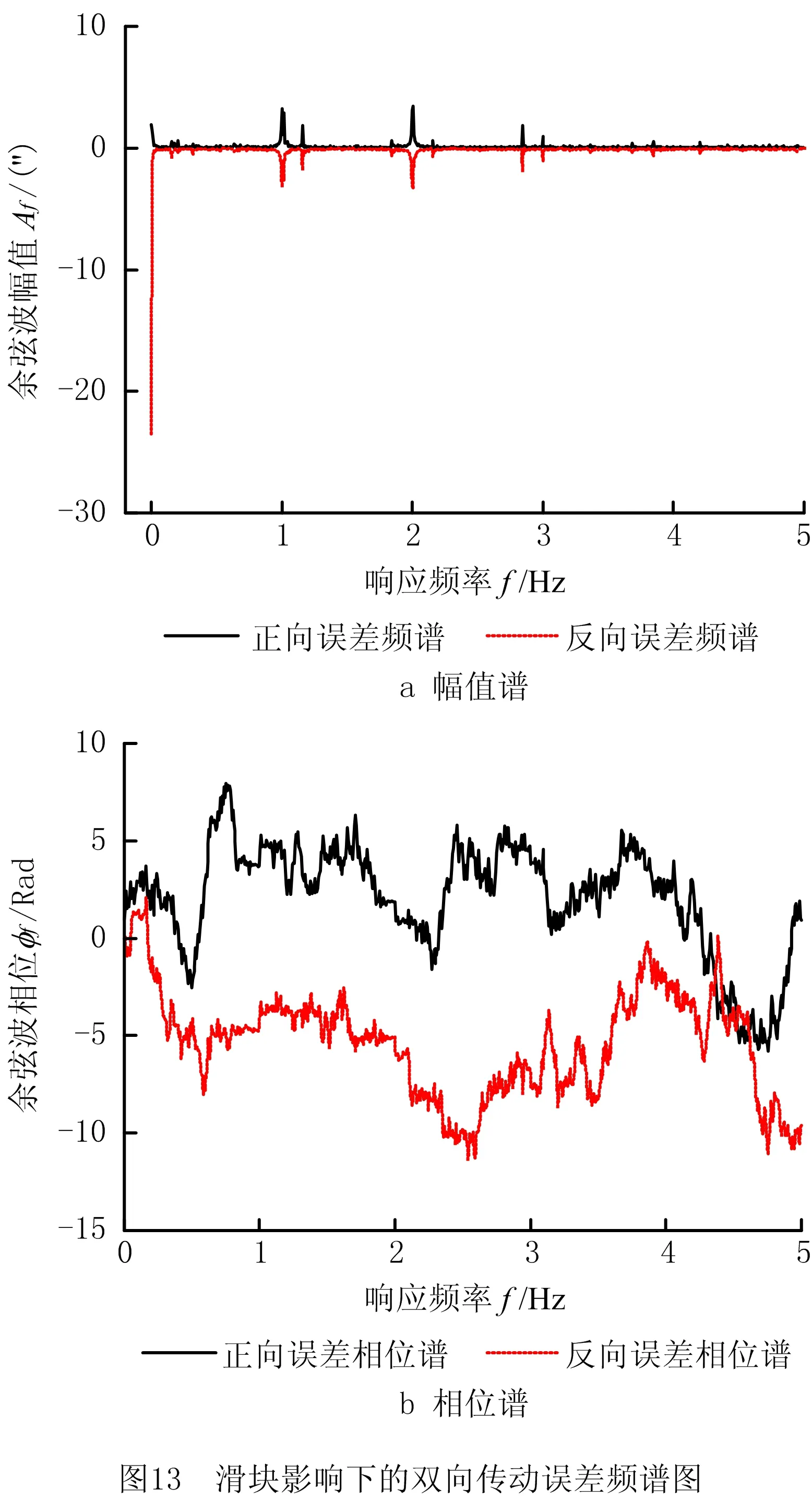
表4 不同方案的误差测试结果

根据4.4节内容，对实际主要频率下的误差幅值进行比较，结果如表5所示。表中差值由方案二结果减去方案一结果获得，对误差常量做绝对值处理以分析其大小的变化。从正向结果可以看出，方案二中的误差常量减小了0.96″，约33%。波发生器转频位置附近没有幅值响应。刚轮啮频位置幅值减小了1.18″，接近27%。刚轮啮频二倍频位置幅值减小了1.46″，接近30%。反向结果与正向结果大体相近，但误差常量比方案一增大了约10″，这是由滑块的间隙引起的。

表5 不同方案的频域幅值结果

表5中0.559 35Hz是以波发生器转频为主导叠加而成的频率，因此其对误差形貌的影响与波发生器转频接近。根据第1章中分析，凸轮随动偏差将引起一个误差常量，凸轮定向偏差将引起其二倍转频2fwg下的偏差，凸轮的综合偏差将引起其转频fwg下的偏差。根据第2章中分析，频率接近的刚轮啮频余弦和柔轮啮频余弦叠加将使得传动误差整体呈纺锤形拍频，再叠加波发生器转频fwg余弦成分后，传动误差整体将呈现出纺锤形加波浪形的综合拍频形貌特征。图9中正反向误差均具有图6d所示的纺锤形加波浪形拍频特征，图11中的正反向误差更接近于图6c所示的纺锤形拍频特征。

方案二中滑块式波发生器可以有效地消除凸轮误差的影响，即更换滑块式波发生器后，传动误差的常量部分将减小，波发生器转频处的幅值响应将消失，刚轮啮频处的幅值响应将减弱。拍频特征将由波浪加纺锤的组合形状转为更接近纺锤。表4和表5的结果验证了第1章和第2章中波发生器偏差对传动误差大小和形状影响分析的准确性。

5.2 正反向频域结果对回程误差的影响

前述分析中图9和图11体现出减速器连续正反向运转时，其传动误差在时域和空域上存在着一定的差异，这也导致了回程误差的出现。图10和图13在频域显示了双向传动误差的幅值和相位的变化。可以看出，正反向运转中的传动误差主要频率没有变化。对实际主要频率的幅值响应和相位进行分析，结果如表6和表7所示。

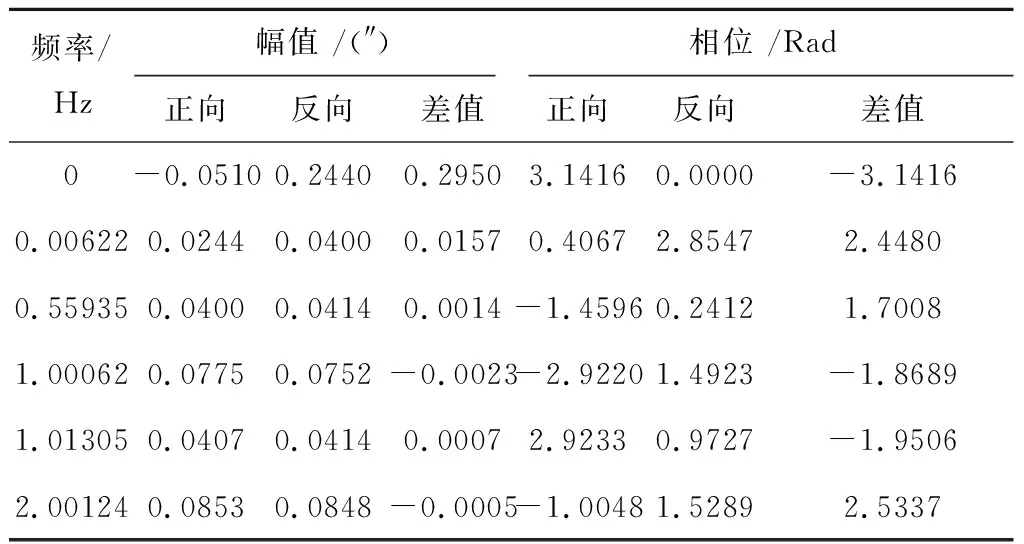
表6 方案一的双向幅值相位

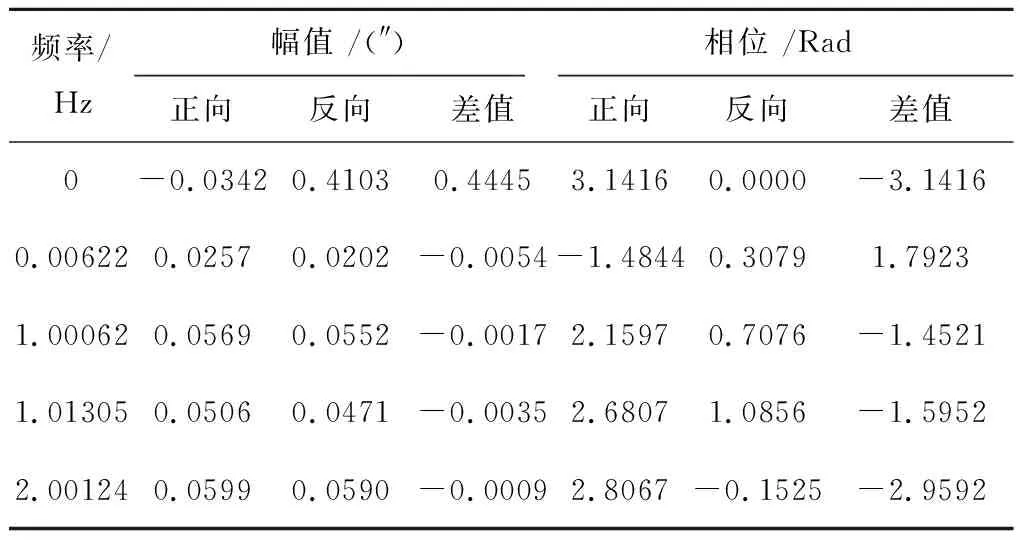
表7 方案二的双向幅值相位

表6和表7中反向相位依然乘-1进行分析，差值是反向结果减去正向结果获得，其中相位差值在±π内进行评价体现误差源的偏差方向变化。表6和表7中显示，反向误差常量相对正向有较大增加是由于减速器各组件间的间隙引起的，尤其滑块式凸轮波发生器的间隙导致方案二中的反向误差常量增幅一体式凸轮的2倍以上。各频率成分幅值变化较小，但其相位差异显著。因此，相位变化是导致各余弦波叠加后最终结果差异的主要原因，表现为图9b和图11a中正反向传动误差整体形态的差异。相位变化进一步也影响了图9c和图11b中回程误差的结果，是除间隙带来的误差常量变化外产生回程误差的另一主要因素。

除此之外，可以关注到波发生器定向偏差和刚轮综合偏差引起的传动误差频率相同。尽管这两个误差源叠加后的误差频率不变，但不同的相位差将导致不同的叠加效果。相位相同时，叠加误差为两幅值之和；相位相差π时，叠加误差为两幅值之差。可知，不仅可以通过改善波发生器和刚轮的偏差来减小传动误差，合理的偏差方向组合也可以通过相位调整起到减小传动误差的作用。因此，误差相位有进一步研究的价值。

6 结束语

本文进行了谐波齿轮误差来源及频率特性分析，给出了传动误差主成分余弦表达式，并对不同成分组合下的拍频效果进行了分析。通过实验验证了理论分析的准确性。主要结论如下：

(1) 谐波齿轮的传动误差主要由波发生器、柔轮、刚轮的综合偏差造成。理论基础主频成分包括柔轮转频、波发生器转频、柔轮啮频和刚轮啮频等。

(2) 波发生器转频误差与刚轮啮频误差形成了二倍关系，是导致传动误差出现大小波现象的因素之一；波发生器转频误差与柔轮啮频误差形成了近似二倍关系，是导致传动误差在大小波现象基础上出现波浪形拍频特征的因素之一；刚轮啮频与柔轮啮频非常接近，是导致传动误差具有纺锤形拍频特征的因素之一。

(3) 理论主频成分余弦叠加仅反映了实际传动误差的整体拍频特性，而幅值响应显著的理论主频成分及其影响下的实际主频成分余弦叠加能够重构出传动误差的整体拍频特征和近似幅值大小。因此，分析理论主频成分改善其误差来源是改进谐波齿轮传动误差的有效手段。

(4) 往复运转时各余弦成分幅值变化不大，但相位变化明显，相位变化导致双向传动误差的形貌差异，是产生回程误差的主要因素之一。

后续可继续对传动误差各主频余弦波相位的形成机理展开研究，结合波的叠加特性，进一步改善谐波齿轮的传动误差和回程误差。