二维间断有限元水动力模型与波浪模型实时耦合研究

郭江华, 孔令臣，张庆河，王容基，冉国全

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中交天津港湾工程设计院有限公司，天津 300461；3.中冶赛迪重庆信息技术有限公司，重庆 400013)

间断有限元(Discontinuous Galerkin，DG)方法具有高阶精度和局部守恒性，对复杂地形有很好的适应性和易于并行[1]，近年来得到了越来越广泛的应用[2-7]。就二维水动力模拟而言，Aizinger和Dawson[8]较早建立了间断有限元模型，Kubatko等[9]将hp自适应间断有限元模型应用于以对流为主的水体运动模拟，Brus等[10]将高阶间断有限元应用于海岸水动力学问题。针对河口海岸浅水流动，比利时的鲁汶大学利用DG开发了SLIM非结构化网格二维和三维水动力模型，并应用于Fly河污染淤泥入侵Torres海峡的模拟[11]、Titicaca湖藻华模拟预测[12]、湄公河下游河流来沙对河口环境特性影响[13]等一系列研究，其中的二维模块应用于珊瑚礁海域大范围潮流模拟[14-16]。天津大学团队提出了一种任意非结构化网格无积分DG方法[17]，并相继开发了水动力、泥沙等数值模型[18-19]。值得指出的是，在近岸海洋环境条件下，波浪与水流耦合作用往往对波浪传播和水流运动有着重要影响，因此目前基于有限体积、有限元或有限差分法建立的共享二维和三维水动力模型，如FVCOM、Delft3D、TELEMAC、ROMS、ADCIRC等均通过不同方法实现了实时波流耦合模拟[20-24]，而现有DG水动力模型尚缺乏针对波流耦合模拟的研究。

为此，本文将借鉴已有波流耦合模型的实现方法，在李文俊等[18]建立的二维非结构化网格无积分间断有限元水动力模型的基础上，采用我国清华大学自主开发的C-Coupler2耦合器与第三代波浪模型SWAN进行实时双向耦合，建立波浪与节点间断有限元二维水动力的实时波流耦合模型。

1 二维波流耦合模型

1.1 水动力模型及其DG离散

水流控制方程为如下浅水方程

(1)

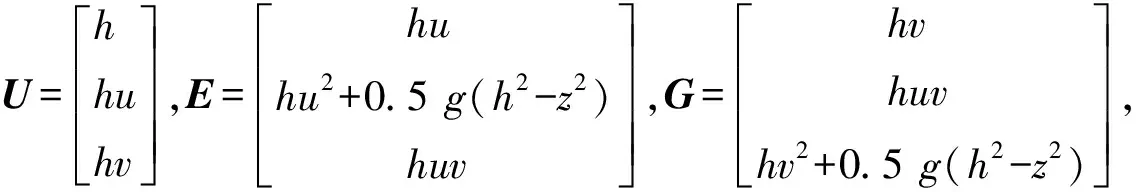
(2)

式中：ρw为流体密度；z为底坡高程；τbx和τby分别为水底床面沿x和y方向的摩阻应力；DFx和DFy为波流共同作用下的水平扩散项。Sxx、Sxy、Syx、Syy为沿水深积分的波浪辐射应力分量，如式(3)所示

(3)

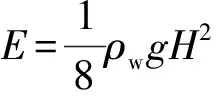
(4)

式中：Er为水滚动能。

方程的离散采用DG方法，首先将计算域划分为Ne个不重叠单元，对于第k个单元Γk，满足式(1)，在Γk上最高不超过p阶的局部多项式空间xp(Γk)上选择一组基函数Φk(x)，用以对精确解近似，使得残差最小，残差方程如下

(5)

(6)

对式(6)应用两次分部积分及格林公式可得到如下方程形式

(7)

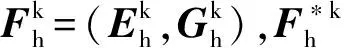
将解用基函数表示，经过推导可得空间半离散形式

(8)

式中：Mk为单元总体质量矩阵；Dk,*为在*方向的微分矩阵；Me,k为单元内每条边对应的质量矩阵。最后采用显式二阶Runge-Kutta方法对时间进行离散。

1.2 波浪模型

波浪模型采用第三代海浪模型SWAN(Simulation WAves Nearshore)，可用于模拟海洋、河口、海岸和湖泊等水域中波浪的生成与传播[26-27]。SWAN采用二维波作用谱密度来描述随机波浪场，在笛卡尔坐标下模型控制方程如下

(9)

式中：左端第一项表示波作用量N随时间变化，第二项和第三项表示波作用量以速度cx、cy在x和y方向上的传播，第四项表示波作用量N在相对频率σ空间上的变化，第五项表示水流及地形变化引起的波浪折射，右端项表示源项，包括风能输入和波浪相互作用波浪破碎、底摩阻等引起的能量损耗。关于SWAN模型的数值离散，详见文献[27]。

1.3 波流耦合的实现

波流耦合利用C-Coupler2耦合器实现，耦合框架如图1所示。C-Coupler2是由我国清华大学独立自主研发的地球模式耦合器，C-Coupler2耦合器具有并行软件架构，可生成适用不同耦合模式的耦合器实例[28-29]。在本耦合系统中，水动力模型和波浪模型均采用相同的非结构化网格，二者同时独立运行，根据指定的耦合频率通过C-Coupler2实现流场与波浪场物理量交换，其中，二维水动力模型向SWAN模型提供水位η、x和y方向上的垂向平均流速u和v，同时SWAN提供有效波高Hs、波向θ和破波率Qb等波浪要素。

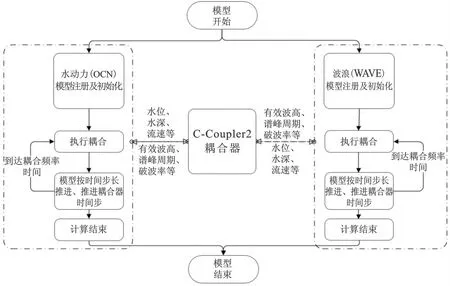
图1 耦合框架图

2 模型验证

波浪在近岸区域传播时，随着地形变化，会发生浅水变形、折射、绕射以及波浪破碎等波浪变形现象，在此过程中波高发生变化，并通过波浪辐射应力引起近岸波浪流现象。同时，近岸区水位变化与水流流速也会明显引起波浪场的变化，波流耦合模型应能够合理描述受水流影响的波浪近岸传播变形及波浪影响下的近岸水流。为此下面通过系列已有实验验证波流耦合模型的合理性。

2.1 裂流通道波生流实验

Hamm在水池中进行了裂流通道地形波生流实验[30]，实验在水池中进行，地形如图2所示，中间有下凹的裂流通道，坡度为1:30，入射波浪采用方向谱，其表达式为S(f,θ)=Sγ(f)cosnθ，Sγ采用JONSWAP谱，γ取为3.3，方向分布参数n取6，入射波高0.07 m，谱峰周期1.25 s，破波指标γ=0.71。

图2 裂流通道地形及波浪场

波浪在向岸传播过程中，由于地形变化产生折射，并且产生波能辐聚和辐散，波浪传播矢量场如图2所示，与不耦合模型相比，耦合模型受水流作用明显，在裂流通道附近波高增加。在破波带内，由于下凹地形影响，波浪增水在沿岸形成水位差异产生的静压力差形成沿岸流，沿岸流在此区域汇合，以裂流形式流向外海，如图3所示。图4显示了通过裂流中轴线处(Y=15 m)的波高分布，其中实线和虚线分别是通过耦合和非耦合模型计算的波高沿程变化图，可以看出，如果不考虑水流的耦合作用，单纯波浪模型不能反映出裂流通道内波浪的变化。实际上，由于裂流通道处波浪受到和波浪传播方向相反的逆向水流影响，波高明显增加，只有利用波流耦合模型才能获得与实验结果一致的波高分布。

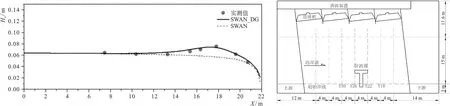
图4 裂流通道轴线波高沿程变化

2.2 T型堤波生流实验

Gravens和Wang[31]在波浪水池中进行了T型防波堤掩护下的动床实验，以研究斜向不规则波产生沿岸流作用下泥沙输移。实验布置如图5所示，防波堤位于Y22与Y26之间区域，由四台造波机进行造波，有效波高为0.22 m，周期1.5 s，波向角为6.5，破波指标γ=0.73。实验过程中测量了断面处的沿岸流流速与波高，这里采用靠近防波堤的Y22、Y26测点处的沿岸流流速与波高进行验证。

模型计算结果与测量结果吻合良好，如图6、图7所示，说明模型能够反映出正确的水动力规律和T型堤附近波浪变形规律。在T型堤掩护区，波浪以绕射形式传入，掩护区内外辐射应力梯度较大，于是在防波堤右侧形成顺时针环流，而左侧由于防波堤阻挡沿岸流形成了逆时针环流，如图8。因此本文波流耦合模型可以应用于复杂地形，计算结果合理且与实验结果相符合。

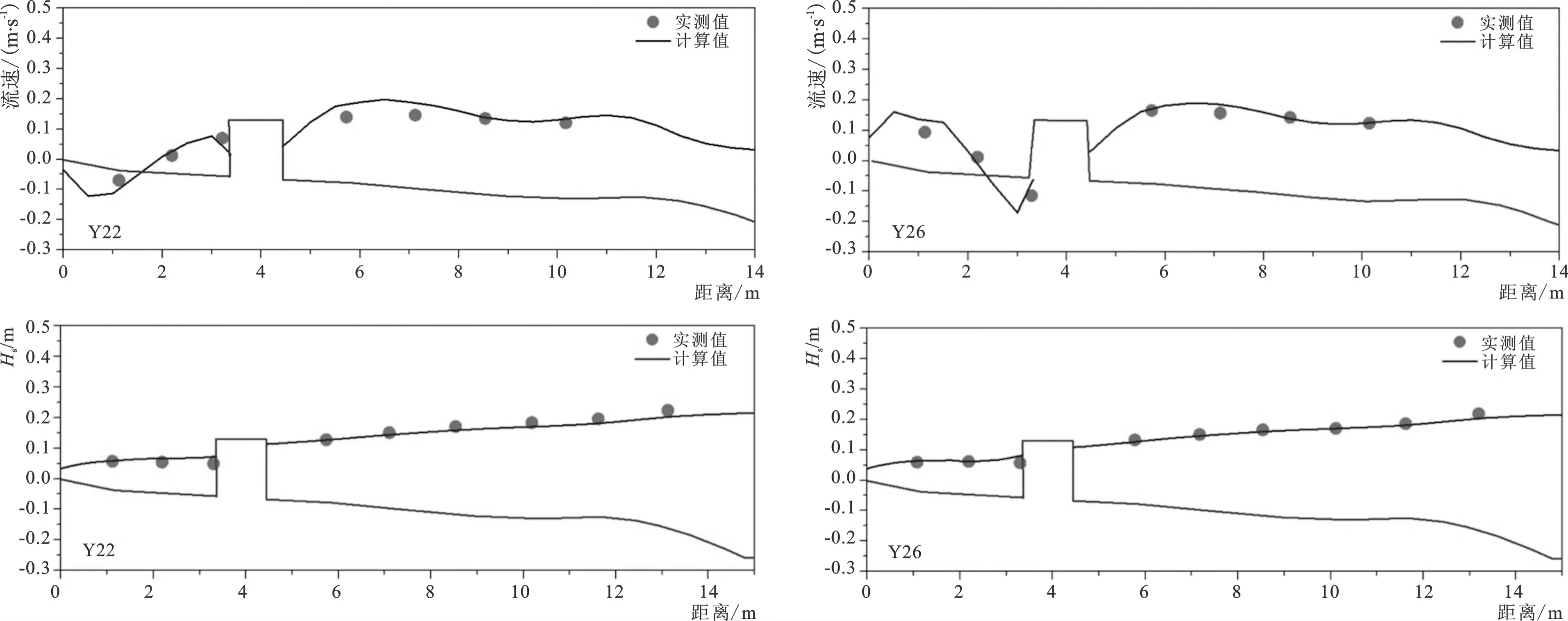
图6 Y22断面沿岸流流速分布及断面波高沿程分布

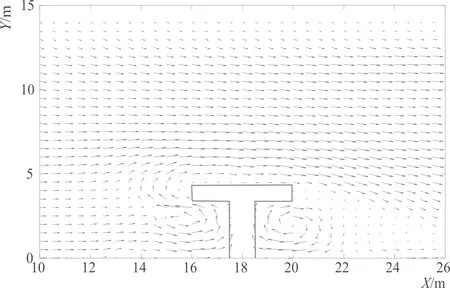
图8 T型堤局部流场

3 模型应用

将模型应用于黄骅港大风过程中水动力特性研究。根据实测资料显示，在2006年3月10日到3月14日期间，渤海区域内出现较大风速，本文将对此时间段内黄骅港附近海域波流动力特性进行研究。波浪和水动力计算均采用为大、小模型嵌套的方式，采用相同的三角形网格，大小模型网格划分如图9，其中大模型节点数为27 221，网格单元数为52 522；小模型节点数为17 652，网格单元数34 320，水动力计算模型采用2阶精度。图9～图11中A、B分别为波浪测站与潮位测站，P0、P1、P2点分别为0 m、-2 m、-4 m等深线(以平均水面为基准)上的计算测点。波浪和水动力计算均考虑风场作用，采用ERA5风场数据，空间分辨率为0.25°，时间分辨率为1 h。

图9 大、小模型网格划分与各测点位置

根据潮位与波高验证结果(图10、图11)，计算结果与实测潮位和波高吻合良好，说明模型能够合理地模拟大风过程中黄骅港区域潮流与波浪的运动。

图10 潮位验证(以平均水面为基准，0时刻为2006-03-11 12:00)

由于波浪破碎过程中将伴随能量损失，导致波高等波要素发生变化，从而在近岸区域出现明显的增减水现象。图12为P0、P1和P2点的水位历时曲线，其中实线和虚线分别为耦合模型和未耦合模型计算结果，可以看出由于波浪作用，近岸地区的水位相对于只考虑风增水的水动力模型会明显增加，即产生波浪增水，P0点(0 m等深线)增水将近0.2 m，P1点(-2 m等深线)最高增水0.1 m，并且随着水深增加增水减小。

图12 各点水位变化

图13为点P0、P1和P2的波浪历时曲线，其中实线和虚线分别为耦合模型和未耦合模型计算结果，结果显示潮位变化和潮流对波浪的作用显著，其中P1点(-2 m等深线)区域波高增大可达0.8 m左右，并且当水深越小时作用越明显。

图13 各点波高变化

总体而言，波流相互作用越近岸越明显，随着水深的增加而减弱。相较于非耦合模型，耦合模型的计算结果更为合理。

4 结论与展望

本文在李文俊等[18]建立的无积分节点间断有限元二维水动力模型的基础上，利用C-Coupler2耦合器与波浪模型SWAN进行实时耦合，建立了二维波流耦合间断有限元模型。水动力计算中考虑了辐射应力和波面水滚等源项，波浪模型通过实时更新水位、流速等条件，实现了模型的实时双向耦合。模型通过Hamm裂流通道实验、Gravens和Wang的T型防波堤实验进行验证，数值模拟结果与实验结果吻合良好，模型能够反映出由于辐射应力梯度产生的波生沿岸流、由于沿岸不均匀地形产生的裂流和堤后环流、以及水流对波浪传播的影响。将模型应用于黄骅港海域模拟计算，较好地描述了现场波浪和水动力变化过程。

波流作用下海岸泥沙运动和地形演变是海岸动力学关心的重要问题，今后将进一步在波流耦合模型的基础上发展基于间断有限元方法的波流耦合作用下泥沙运动和地形演变模型。