雷诺数对高负荷低压涡轮叶栅流动损失的不确定性影响
罗佳奇,傅文豪,曾先,夏志恒
1. 浙江大学 航空航天学院, 杭州 310027 2. 中国空气动力研究与发展中心, 绵阳 621000
高负荷叶片是降低低压涡轮(LPT)重量的必然选择,但同时导致流动更复杂。高空巡航时,LPT雷诺数较低,叶背层流在速度峰之后将经历膨胀过程,由此产生的逆压梯度极易诱导边界层分离及转捩,导致较大的叶型损失。Howell、Hodson等均指出:LPT叶背损失占总损失的60%以上,主要归因于边界层的分离、转捩及再附。整体上,边界层分离转捩在LPT内部较为常见,相关的影响机理及流动控制研究自2000年以来开展较多,目前仍是国际性研究热点。
在真实工作环境下,航空发动机部件进、出口流动不可避免地会受到环境变化、上下游部件的影响,如:进气道边界层将导致压气机/风扇进口流动发生周向和径向畸变;燃烧不稳定将导致燃烧室出口燃气具有较强的周向和径向非均匀性,对高压涡轮气热固性能有重要的不确定性影响。雷诺数与较多参数有关,当飞行姿态发生变化或受到上下游部件、环境扰动的影响时,雷诺数都将发生不确定性变化。考虑雷诺数及叶片进、出口流动参数不确定性变化的影响,计算叶片平均气动性能及分散度,对于评估叶片气动稳健性及叶片鲁棒性设计具有重要意义。
在不确定性的数值研究中,高效高精度的不确定性量化(UQ)方法及高保真流场数值模拟是关键。已有研究表明:目前应用较为广泛的UQ方法主要是模型方法和灵敏度方法;灵敏度方法更高效,但只适用于小尺度UQ问题;模型方法在大尺度UQ问题中更具有优势。此外,高负荷LPT分离转捩的流动机理非常复杂,近年来,大涡模拟、直接数值模拟在LPT的数值研究中已经初步实现。考虑到不确定性研究需要采用概率统计方法,涉及大量的流场计算,求解定常雷诺平均Navier-Stokes(RANS)方程的流场计算方法更为可行。
1 T106C流动数值模拟
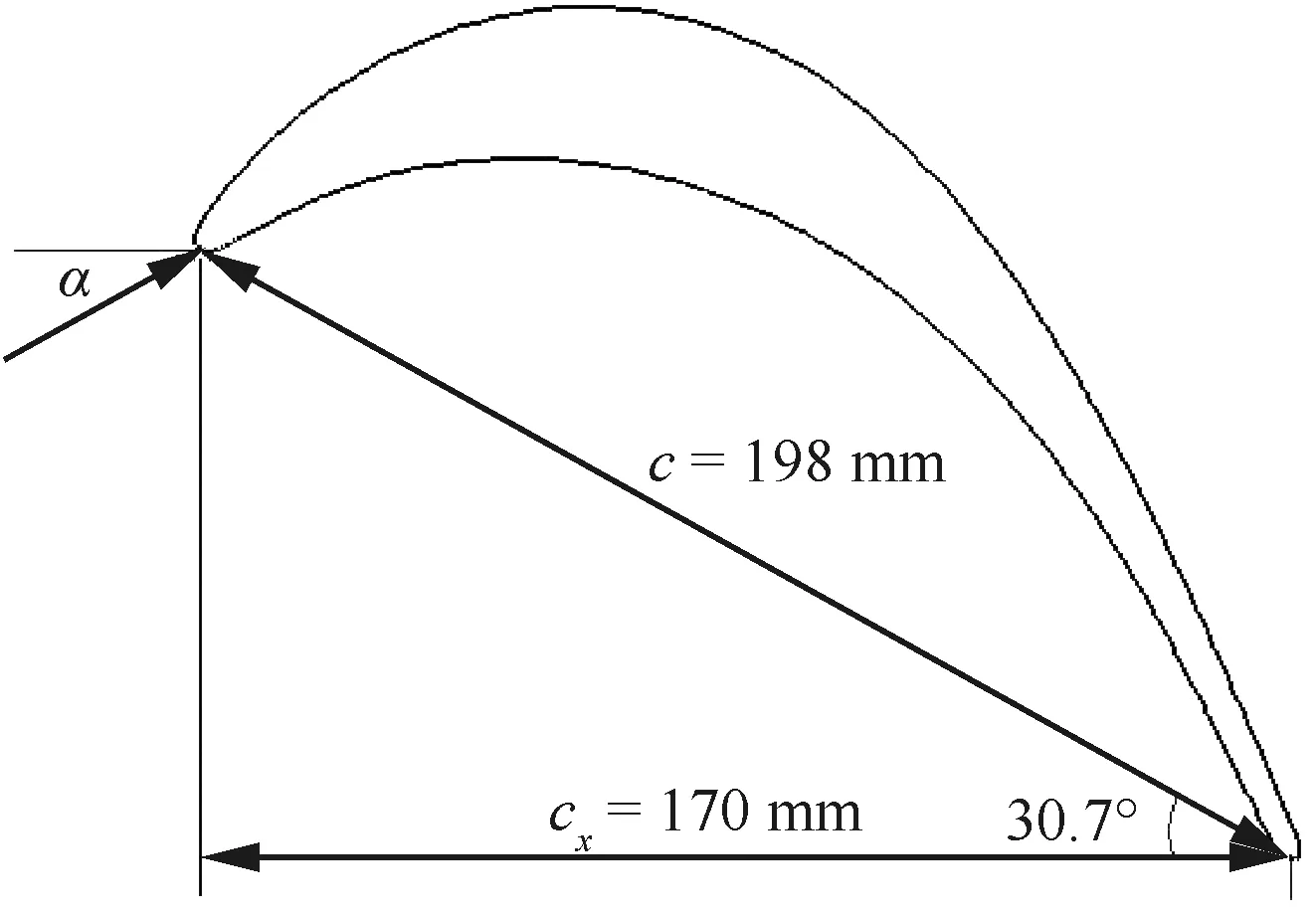
图1 T106C叶栅叶型Fig.1 Profile of T106C cascade
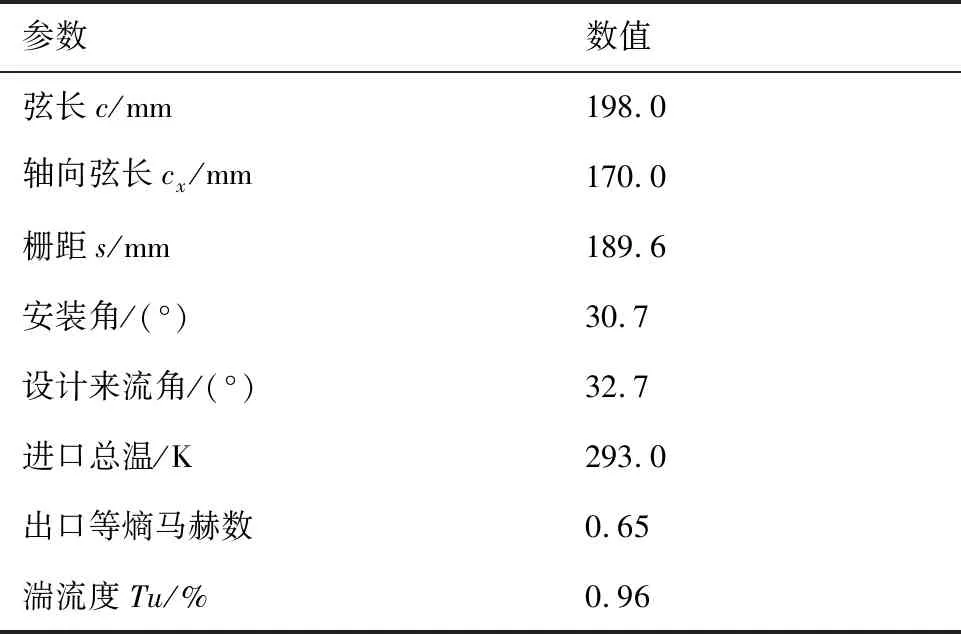
表1 T106C叶栅主要参数Table 1 Specifications of T106C cascade
流场数值模拟采用自研程序,对流通量离散采用Roe格式,通量重构采用三阶迎风;采用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)进行时间推进;采用多重网格加速收敛。为了实现高保真数值模拟,首先确定网格收敛解并进行误差分析。研究中采用表2所示的5套网格及对应的第1层网格壁面距离。图2为动能损失系数(KELC)网格收敛曲线,KELC的定义为
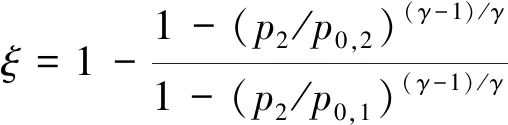
(1)
式中:和分别表示静压和总压;下标1、2分别表示进口和出口;为比热比。
图2中,在每个雷诺数条件下将网格1的计算结果()作为参考值对KELC进行归一化处理,为网格编号。由图可知:随着网格的加密,KELC呈明显收敛趋势;前3套网格的计算结果非常接近,尤其是在低雷诺数条件下,网格3基本收敛。表3将网格3的计算结果()与试验结果()进行了对比,当雷诺数较高时,数值解与试验结果的相对偏差非常小(低于0.5%);随着雷诺数降低,KELC逐渐增加,数值解与试验结果的相对偏差(Δ)也逐渐增大。

表2 T106C计算网格Table 2 Computational grids for T106C
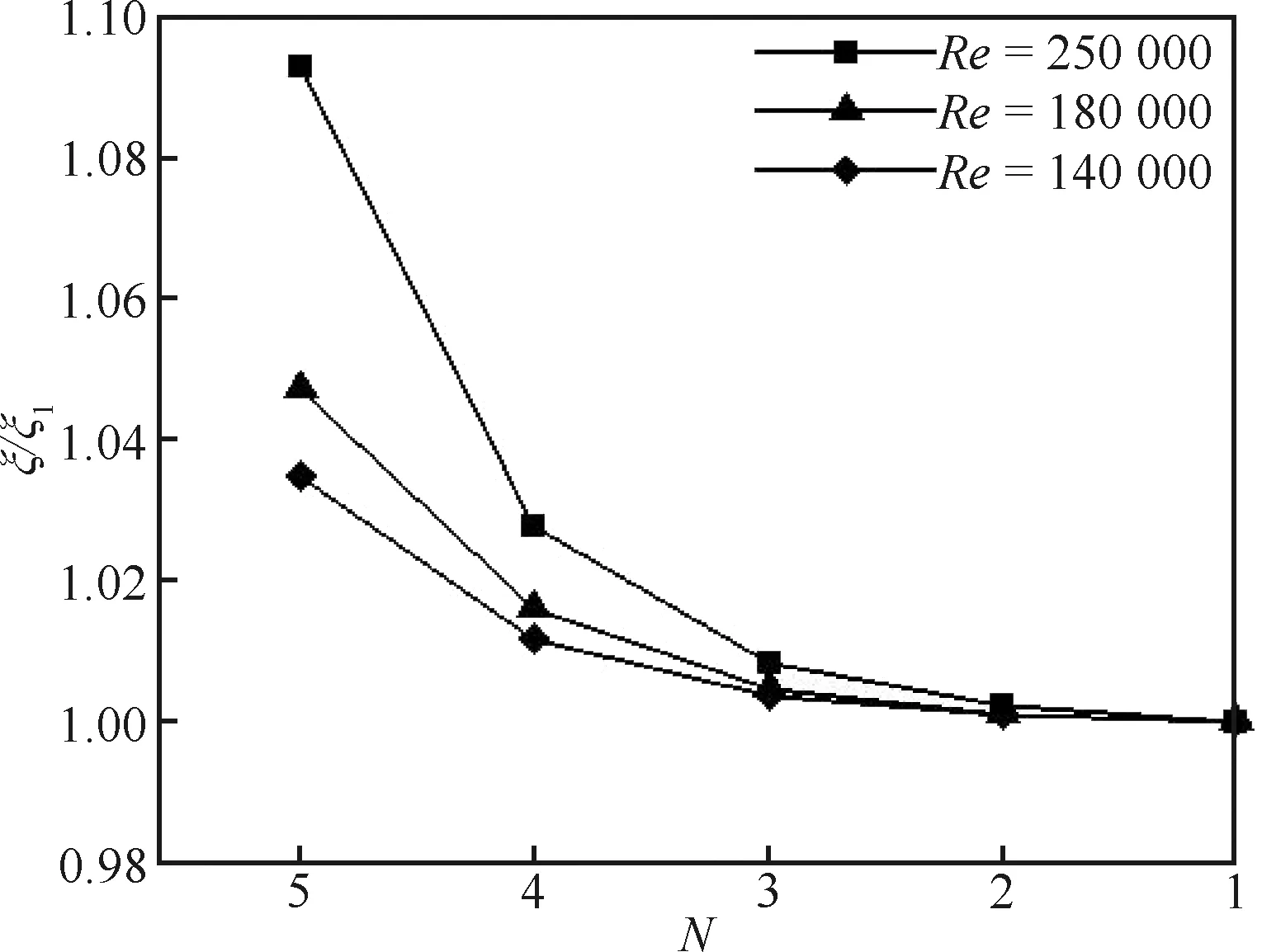
图2 动能损失系数的网格收敛性Fig.2 Grid-independence of KELC
图3为叶面等熵马赫数分布,图中表示出口等熵马赫数,右上角为分离转捩区放大图。除了在叶背前缘附近,网格1和网格3的计算结果与试验结果(Exp)吻合较好,网格5的计算结果与试验结果有一定偏差。此外,由图3(b)可知:数值模拟的转捩完成点明显前移,导致分离泡偏小、KELC偏低。实际上,试验研究发现:随着雷诺数的降低,分离泡不断增大,甚至在叶背出现开式分离泡,流动变得更复杂,给边界层分离转捩的数值模拟带来更大挑战。

表3 动能损失系数对比Table 3 Comparison of KELC
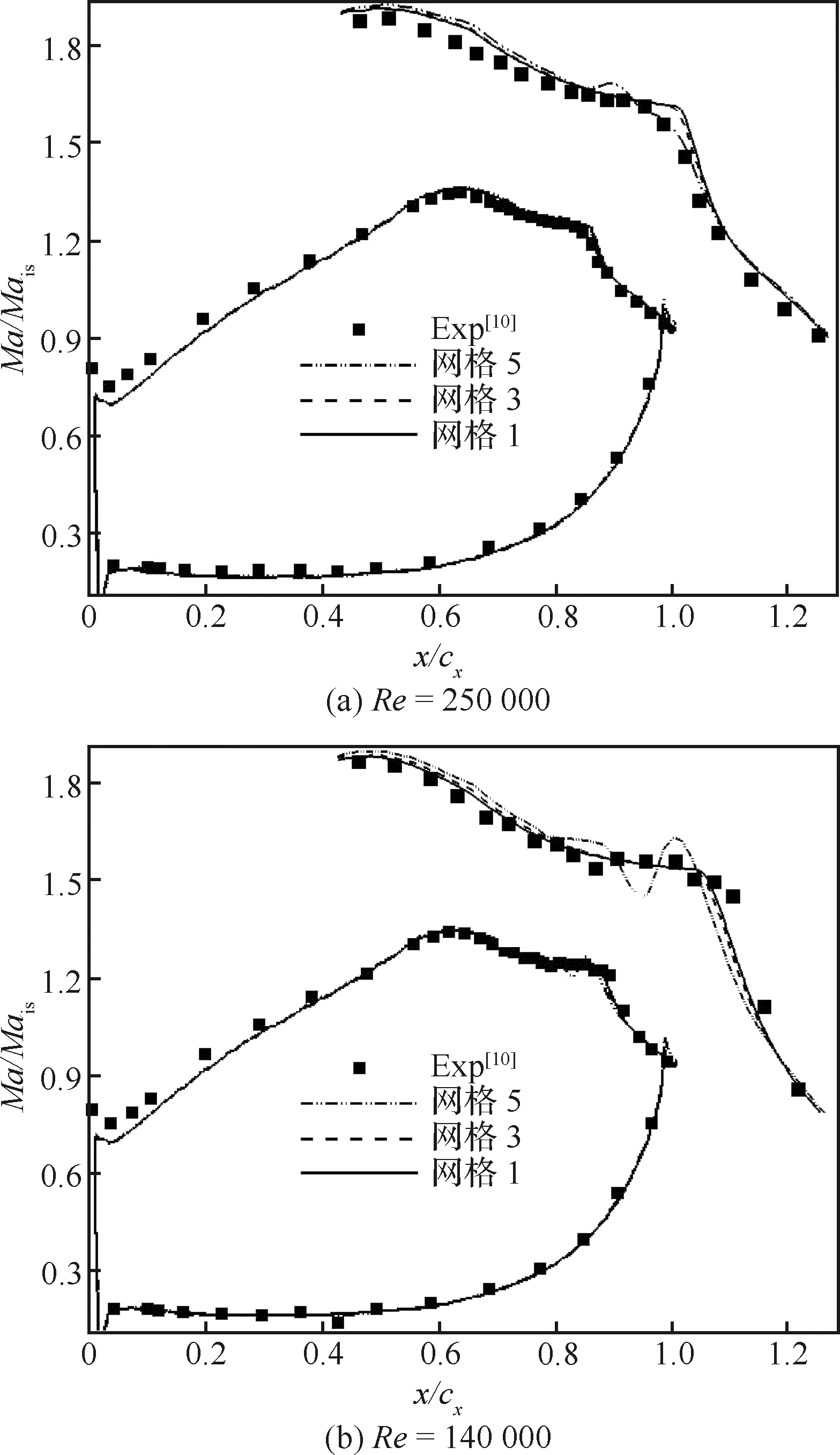
图3 叶面等熵马赫数分布Fig.3 Isentropic Mach number distributions on blade
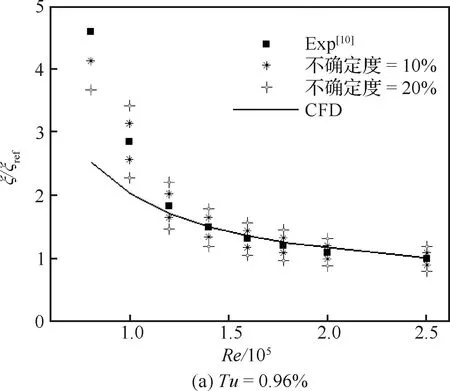
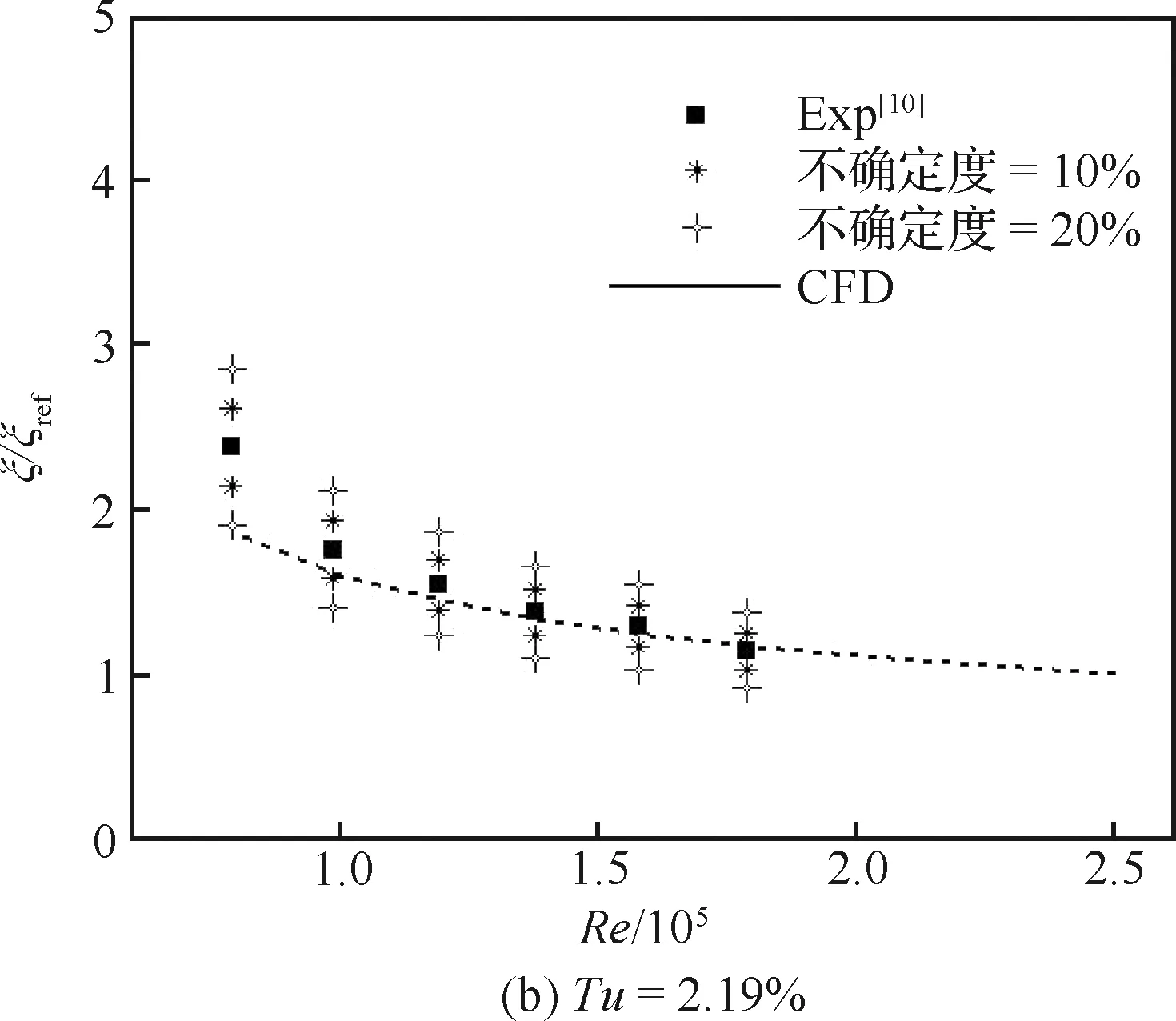
图4 动能损失系数随雷诺数变化曲线Fig.4 Variation curves of KELC with Reynolds numbers
2 KELC不确定性量化
2.1 UQ方法及影响分析
在UQ之前,先分析雷诺数扰动对KELC的影响。试验测量中,出口等熵马赫数和雷诺数的最大不确定度分别为1.2%、1.3%。若考虑飞行姿态或环境变化的影响,雷诺数的不确定性变化将更显著。文中雷诺数的不确定度为20%。
研究中将对比使用二阶灵敏度和代理模型来描述雷诺数扰动范围内KELC的变化规律。由于不确定性参数较少,研究中采用原理简单、易实现的多项式函数来构造代理模型:
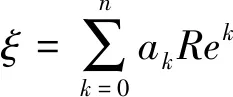
(2)
式中:为多项式系数,为多项式阶数,研究中采用三阶多项式(=3)。
构造代理模型的核心是训练样本选取。研究中采用“弃一交叉验证”法(LOOCV)实现自适应抽样。LOOCV是交叉验证法的一种,主要原理参见文献[27]:在个样本集合中,依次选取一个样本作为测试样本,其他-1个作为训练样本并构造代理模型;由函数响应误差评估各个测试样本所在子空间的模型响应精度。采用该方法,可以向初始样本集合中动态地增加新样本,直至所有样本的LOOCV函数响应误差达到精度要求。
图5(a)、图5(b)分别为高湍流度、低湍流度条件下KELC在雷诺数扰动范围内的变化,Δ表示相对雷诺数变化量。图中,Model表示代理模型结果,Hesse表示二阶灵敏度分析结果。初始样本集合包含5个均匀分布样本,采用LOOCV方法后,扰动边界附近的样本有所增加,所构造的多项式代理模型和数值结果几乎完全重合;此外,低湍流度和低雷诺数条件下,KELC的非线性变化更明显。
研究中还采用直接差分法计算KELC的一阶和二阶灵敏度。扰动后的KELC为
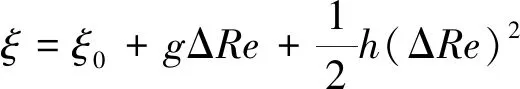
(3)
式中:和分别为一阶、二阶灵敏度;为原始KELC。
由图5可知:当雷诺数扰动较小时,基于灵敏度分析的KELC与数值结果较为接近;当雷诺数扰动增大时,偏差较为明显。此外,低湍流度条件下,灵敏度分析与数值结果之间的偏差也更大。
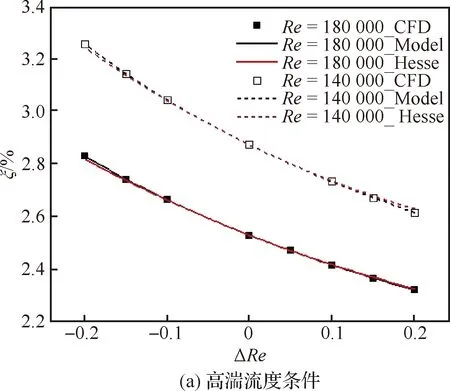
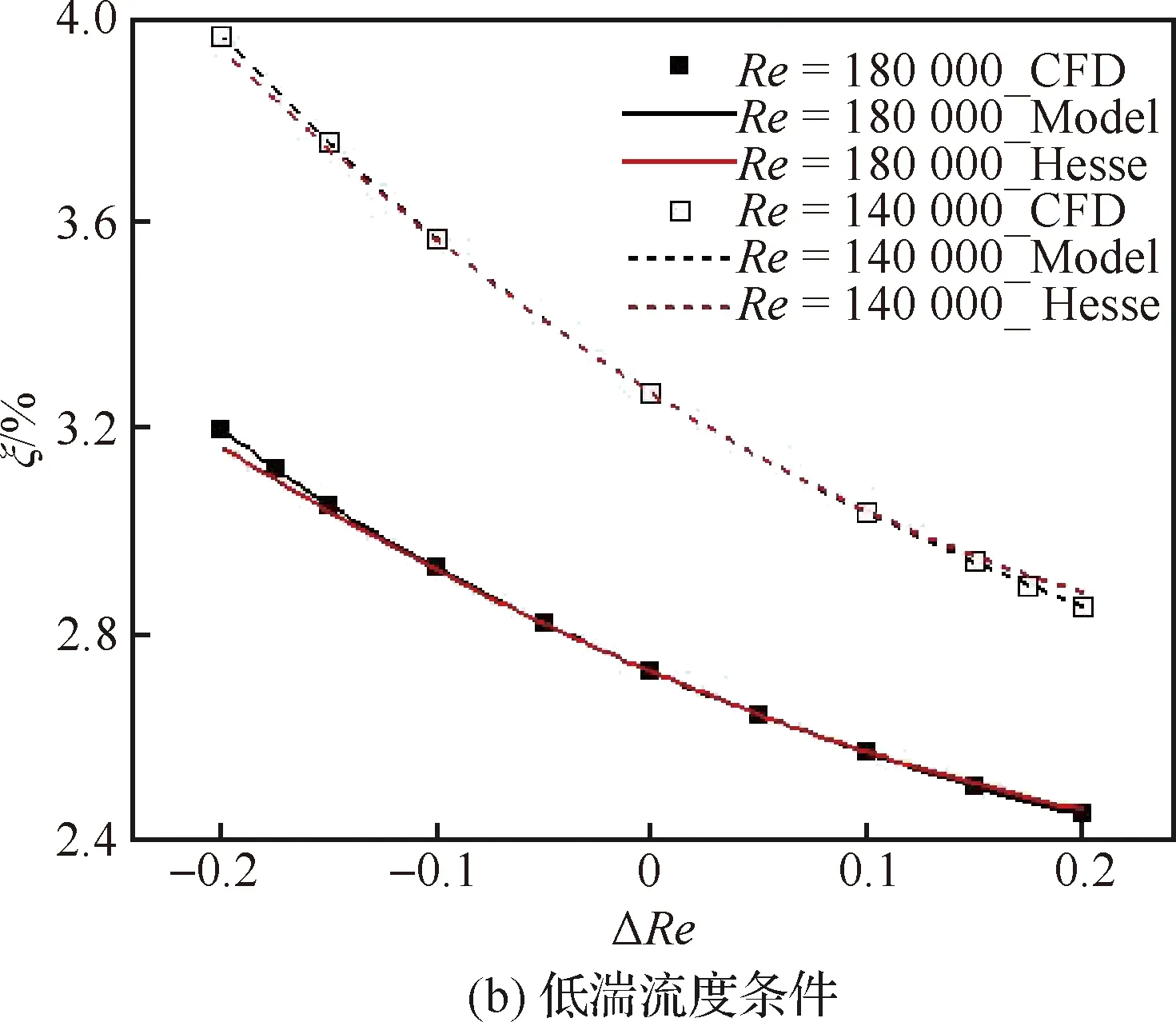
图5 动能损失系数随雷诺数扰动的变化曲线Fig.5 Variation curves of KELC with ΔRe
由上述分析可知:雷诺数的不确定度为20%时,所研究的问题为大尺度不确定性问题,雷诺数扰动对KELC变化具有较强的非线性影响。后续研究中将采用式(2)所示的自适应模型。
2.2 不确定性量化
UQ的目标是在给定的输入参数概率分布的基础上计算输出参数的统计均值()、标准差()等。不同于叶片几何偏差的不确定性问题,确定流动扰动的概率分布难度非常大,需要较长时间内的数据积累。根据随机事件的特点,一般假设流动参数不确定性变化满足以下标准正态分布:
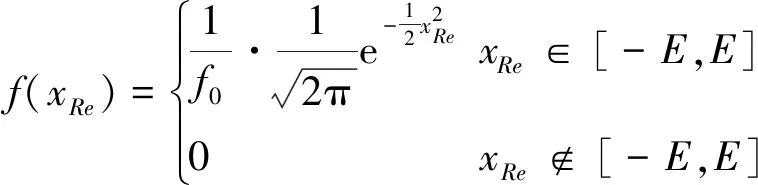
(4)
式中:表示雷诺数扰动量,定义为
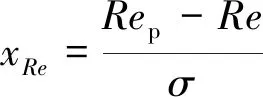
(5)
其中:为雷诺数变化标准差;表示扰动后雷诺数;为截断边界且=2.0;为修正系数,保证标准正态分布的概率密度函数在[-,]区间内的积分为1,当=2.0时,=0.954。
接下来在=180 000的条件下进行UQ。研究中随机生成20万个满足标准正态分布的统计样本,根据式(2)计算统计样本的KELC,再进行统计分析确定KELC变化量的统计均值和标准差,同时还确定其概率密度函数(PDF)。
图6为雷诺数变化量、不同湍流度KELC变化量的PDF。整体上,KELC的PDF已较大程度地偏离了正态分布。如图6(c) 所示:KELC的最大下降量约为10%、最大增加量约为17%,进一步表明雷诺数变化对KELC的非线性影响。当湍流度增加时,KELC的最大变化量显著下降,如图6(b) 所示。上述结果表明:低湍流度时雷诺数变化的非线性影响更显著。此外,当湍流度下降时,KELC的统计均值和标准差明显增大,结果表明:湍流度较低时,考虑雷诺数不确定性影响的叶栅气动性能衰退更严重、气动分散度更大。
研究中还将对比分析满足不同概率分布的雷诺数变化对KELC的不确定性影响。假设雷诺数变化满足以下所示的均匀分布:
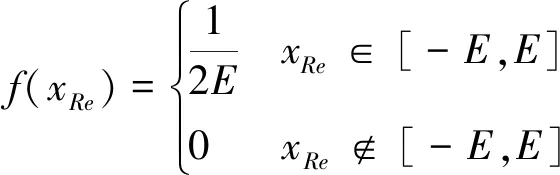
(6)
类似地,=180 000,随机生成20万个满足均匀分布的统计样本。采用相同的方法计算KELC变化量的统计均值、标准差及PDF。
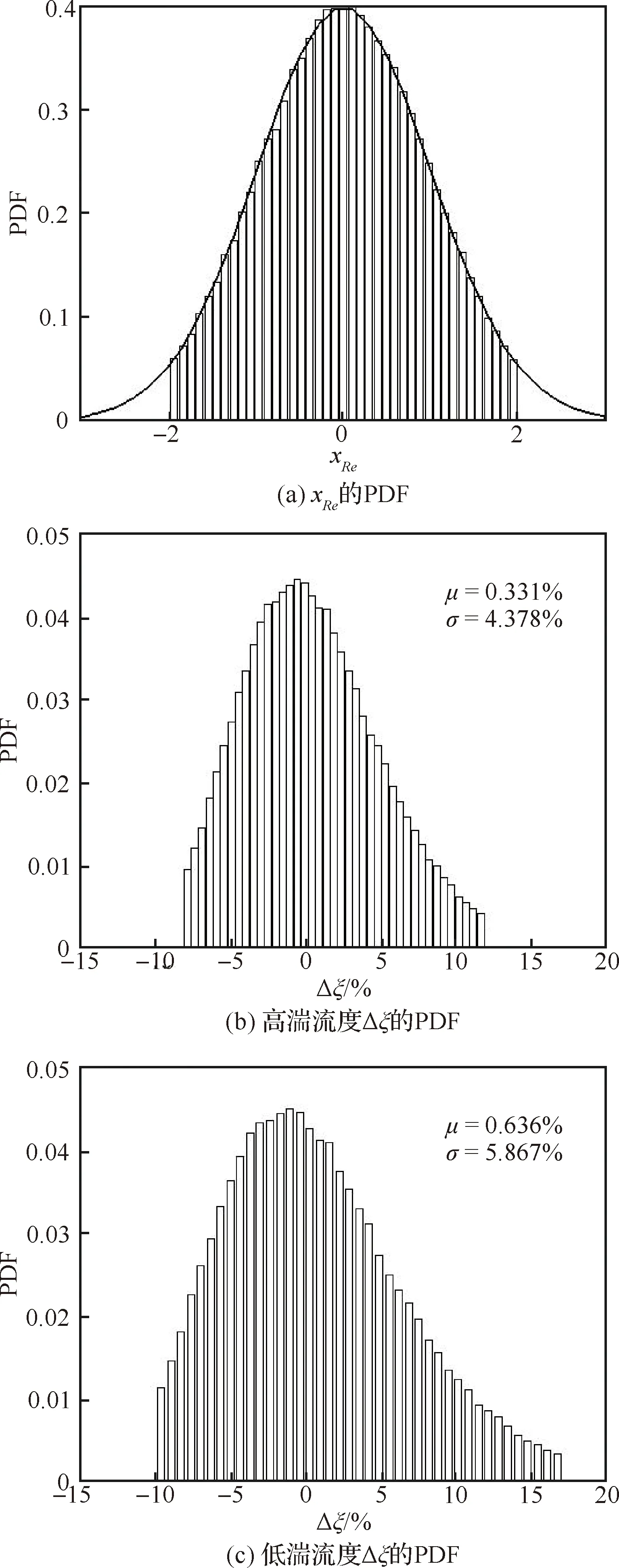
图6 xRe、Δξ的概率统计函数(xRe满足标准正态分布)Fig.6 PDFs of xRe, Δξ(xRe follows standard normal distribution)
图7为雷诺数变化量、不同湍流度时KELC变化量的PDF。整体上,KELC的PDF已完全偏离均匀分布。和图6结果类似,与高湍流度结果对比,在低湍流度条件下,雷诺数变化的非线性影响更显著,考虑雷诺数不确定性影响的叶栅气动分散度更大。值得注意的是:与标准正态分布相比,当雷诺数变化满足均匀分布时,截断边界附近强非线性影响的统计样本更多,导致均匀分布时KELC变化量的统计均值和标准差更大,该叶栅的气动性能衰退更严重、气动分散度更大。
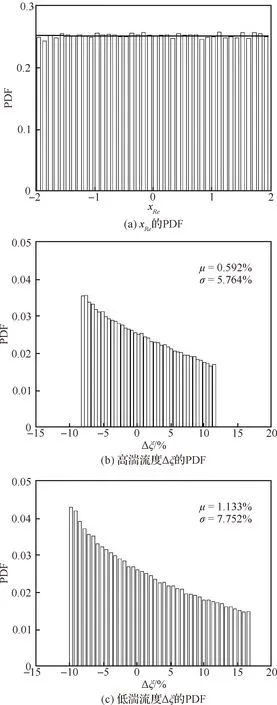
图7 xRe、 Δξ的概率统计函数(xRe满足均匀分布)Fig.7 PDFs of xRe,Δξ(xRe follows uniform distribution)
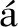
接下来将对比分析不同雷诺数条件下,雷诺数变化对KELC的不确定性影响大小。图8为KELC变化量的统计均值和标准差随雷诺数的变化曲线,对比发现:随着雷诺数的增加,KELC变化量的统计均值和标准差均不断减小,表明:考虑雷诺数不确定性影响的叶栅气动性能衰退减弱、气动分散度降低;此外,均匀分布与标准正态分布的KELC统计量之间的偏差也不断减小。导致上述变化的主要原因是叶背分离泡随着雷诺数增大而减小,流动复杂性降低。值得注意的是:KELC变化量的统计均值与雷诺数变化近似呈线性关系,而标准差与雷诺数变化呈弱非线性。

表4 不同湍流度条件下动能损失系数变化量的统计结果Table 4 Statistics of KELC variations under different Tu
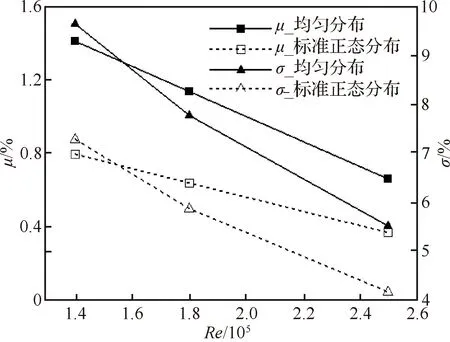
图8 统计均值和标准差随雷诺数的变化曲线Fig.8 Variation curves of statistical mean and variance with Reynolds number
3 流场统计分析
由2.2节可知:在低湍流度条件下,且雷诺数变化满足均匀分布时,雷诺数变化对KELC的不确定性影响最为显著。接下来将采用蒙特卡罗模拟(MCS)对流场进行统计分析,以研究低湍流度条件下(=0.96%)满足均匀分布的雷诺数不确定性作用机理。研究中随机生成200个满足均匀分布的统计样本。大量研究表明:基于MCS的统计分析收敛较慢,往往需要数以千计的统计样本。200个均匀样本可能无法确定收敛的统计结果,但是仍然可以用于定性揭示不确定性作用机理。
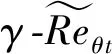
图9 叶背黏应力分布Fig.9 Distribution of viscous shear stress on suction side
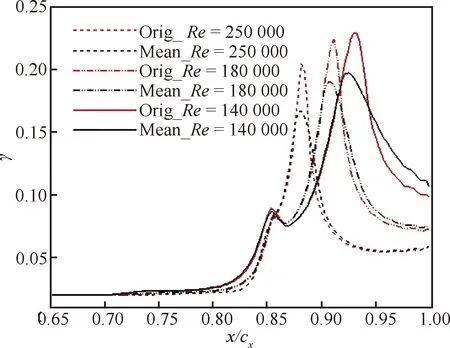
图10 叶背间歇因子分布Fig.10 Distribution of intermittency on suction side
雷诺数变化能改变分离和再附点的位置,原始分离和再附点的黏应力随之发生变化,平均黏应力将大于零。图9中,再附点的平均黏应力远大于零,该现象往往和不同区域流动对雷诺数变化的敏感性不同相关。图10中间歇因子在再附点附近出现峰值,考虑雷诺数不确定性变化的平均间歇因子峰值降低、且峰值位置前移。转捩在再附之前完成,图10中,以=250 000为例,转捩自83%轴向弦长附近开始,在88%轴向弦长之前完成,此区域内统计平均间歇因子与基准值较为接近,表明雷诺数不确定性变化对转捩的影响不如对流动再附明显。但是不同雷诺数条件下,雷诺数不确定性变化对转捩的影响需要进一步深入研究。
为了更好地反映雷诺数变化对叶背流动的影响,图11给出了黏应力相对变化量的统计均值和标准差在叶背的分布,黏应力相对变化量定义为
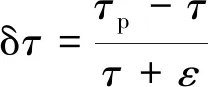
(7)
式中:和τ分别表示扰动后的黏应力和基准黏应力;为小量,避免分离点附近黏应力为0。
由图11可知:不同雷诺数条件下,δ统计量均在分离和再附点出现峰值。由之前分析可知:统计均值在分离和再附点较大的主要原因是雷诺数变化导致分离和再附点位置发生偏移。标准差能反映雷诺数扰动范围内统计样本δ偏离均值的程度,可以用于评估黏应力的敏感性。因此,标准差结果表明:分离和再附点附近的流动对雷诺数变化最为敏感。此外,在再附点之前、86%轴向弦长附近统计量出现局部峰值。由图10可知,此处为转捩完成点;进一步表明雷诺数的不确定性变化对转捩的影响相对较弱。
为了进一步分析不同雷诺数条件下雷诺数不确定性变化对转捩的影响,图12给出了间歇因子相对变化量的标准差云图。由图可知:在靠近壁面的区域I和狭长区域Ⅱ内,间歇因子变化较为显著,但是与黏应力相对变化量的标准差相比,间歇因子相对变化量的标准差较小,表明雷诺数不确定性变化对转捩有一定的影响。随着雷诺数的降低,区域I和区域II内的标准差逐渐增大,表明雷诺数降低时,雷诺数对转捩的不确定性影响逐渐增强。
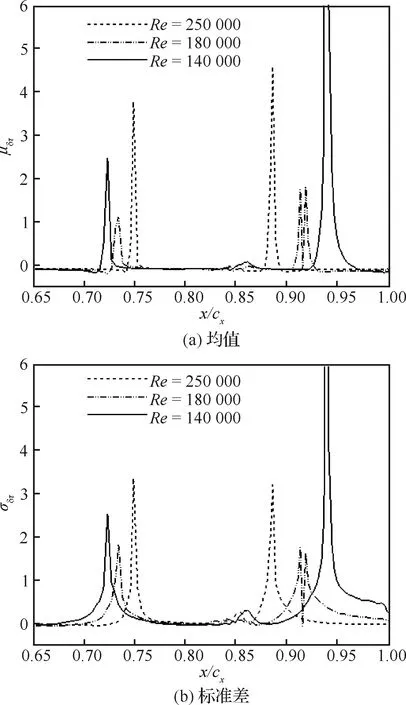
图11 叶背黏应力相对变化量的统计分布Fig.11 Distribution of statistics of relative variations of viscous shear stress on suction side
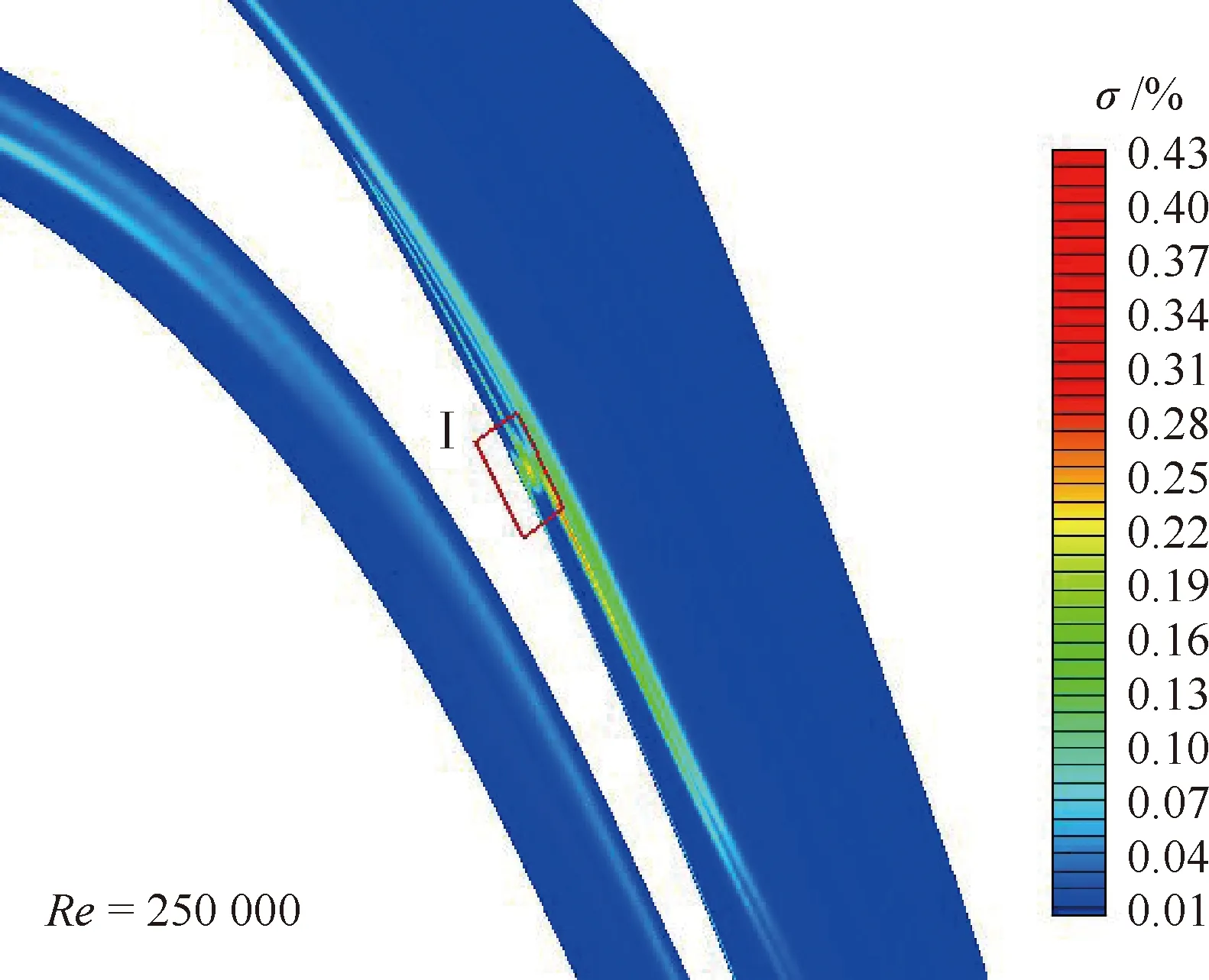
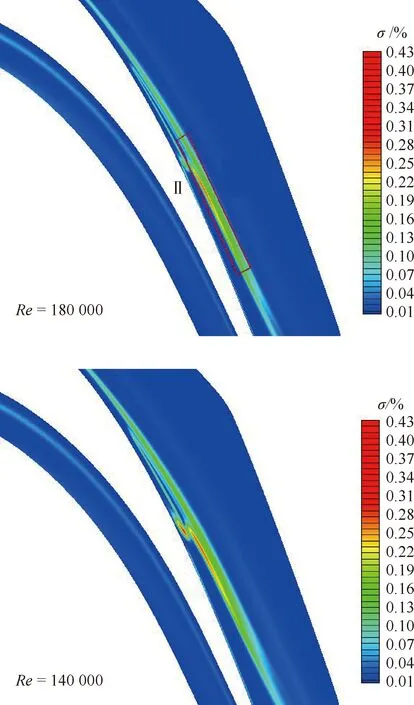
图12 间歇因子相对变化量的标准差云图Fig.12 Contours of statistical variance of relative variations of intermittency factor
4 结 论
2) 当=0.96%和=2.19%时,叶背存在明显边界层分离转捩,此时雷诺数扰动对KELC具有较强的非线性影响;当雷诺数降低时,非线性影响增强;此外,随着湍流度的降低,雷诺数的非线性影响也增强;相对于标准正态分布,均匀分布的雷诺数扰动的非线性影响更强。
3) 当T106C叶背出现层流边界层分离转捩时,分离和再附点附近的流动对雷诺数变化较为敏感,再附点附近流动的敏感性更强;随着雷诺数降低,分离、转捩和再附的敏感性均增强,这是雷诺数对KELC不确定性影响的根源。

