电动客车AMT换挡执行机构状态估计及参数辨识*

林 程，易 江，田 雨

（1. 电动车辆国家工程实验室，北京 100081；2. 北京电动车辆协同创新中心，北京 100081）

前言

能源安全和环境污染一直是我国快速发展过程中所面临的挑战，2020 年国务院办公厅印发的《新能源汽车产业发展规划（2021-2035年）》明确提出了大力发展新能源汽车并提出了全面实现电驱动化，到2025 年公共交通领域的纯电动商用车占比将超过3 成，从国情、国家政策、实际使用场景的角度出发，研究高效、高性能的电驱动系统势在必行。商用车集中式电驱动系统构型在国内属于比较成熟的方案。但是无变速装置的单电机构型已经无法同时满足大功率和大转矩的高性能需求，针对这一问题，文献［7］中提出了一种双电机匹配2 挡变速装置的高性能电驱动系统来满足整车对驱动系统高性能的要求。

匹配变速器的电驱动系统的换挡性能影响到了整个系统的性能发挥。近年来国内外学者对换挡性能的提升做了一些研究。文献［10］中提出基于SMC的换挡控制方法来解决执行机构的间隙和换挡阻力未知导致的换挡性能下降的问题。文献［11］中开发了双层换挡控制策略来提升DCT 动力系统的换挡性能，上层控制器确定离合器和发动机的最佳转矩轨线，下层控制器控制每个执行器跟踪确定的最佳轨线。文献［12］中研究了重型汽车动力系统的鲁棒换挡控制策略，针对不同的换挡过程推导出了3 种不同的鲁棒自适应控制率来减小换挡过程的输出转矩降低换挡冲击实现平滑换挡。文献［13］中将换挡冲击度和换挡冲击度的变化率作为性能指标，通过求解多项式获取最佳的换挡控制策略。文献［14］中提出了一种动态滑模自抗扰控制算法，该算法将系统所有的不确定性因素作为扰动项然后利用扩张观测器观测出来，以扰动补偿的形式消除扰动带来的干扰。文献［15］中研究了换挡执行机构的位置精确控制，建立了换挡执行机构的模糊控制方法，实现换挡执行机构的快速平稳控制。文献［16］中设计了滑模控制器对换挡过程的位置进行精确跟踪控制。文献［17］中提出了基于中值-卡尔曼混合滤波的换挡拨叉运动状态的估计方法，对换挡拨叉的运动速度进行估计以此来提升换挡过程中换挡拨叉的控制精度。

尽管很多学者对换挡控制策略优化做了大量研究工作，这些研究工作都是基于准确的模型开展的，但是有些模型参数是时变的，由于机械磨损存在，导致了换挡执行机构的结构参数的变化，影响了控制模型的精度使得换挡控制策略的鲁棒性变差。此外，由于换挡机构的使用多数暴露在强电磁干扰环境下，使得观测信号的采集存在一定的误差，影响了换挡性能。因此，在聚焦换挡控制策略优化的同时还需要关注控制模型的准确性，对可能时变的参数进行辨识。

近年来不少学者对模型参数的辨识做了不少研究工作。文献［19］中设计了基于容积卡尔曼滤波的状态观测器，用来对车辆的质量和道路坡度进行辨识。文献［20］中采用变遗忘因子的最小二乘法进行坡度和质量辨识。文献［21］中设计了改进的最小二乘法，设置坡度和车辆负载的遗忘因子权重对坡度和车辆负载进行辨识。文献［22］和文献［23］中采用卡尔曼滤波算法对车辆的质量和坡度进行辨识研究。文献［24］中设计了基于双卡尔曼的分层估计方法，对车辆的状态和参数进行估计。文献［25］中设计了基于HIF-EKF 算法和基于DHIF 算法的车辆参数联合辨识方法。但是上述方法主要用于车辆的状态估计和参数辨识，对换挡执行机构参数辨识的研究并不普遍，此外，在系统模型高度非线性化、系统噪声特性未知的情况下，上述方法会存在一定的局限性。

为降低系统参数时变对换挡性能的影响，在考虑系统模型高度非线性、系统噪声特性未知的情况下，本文中提出了一种基于非线性HIF（non-linear HIF，NHIF）算法的分层状态估计和参数辨识的方法（dual non-linear HIF，DNHIF）。上层NHIF估计器对执行机构的状态进行估计，并将结果转移到下层NHIF估计器，下层NHIF估计器利用上层NHIF估计器处理完的状态量作为量测量，利用系统模型作为量测方程对系统参数进行辨识，上下层估计器的协同运行实现了对换挡执行机构的状态估计及结构参数和电性能参数的在线辨识，在修正系统模型准确性的同时解决了系统模型参数时变导致的换挡控制策略鲁棒性差的问题，改善了换挡性能。

1 研究对象描述

1.1 研究对象介绍及研究问题描述

本文中的研究对象是面向2022 年北京冬奥会开发的双电机耦合高效电驱动系统，应用场景见图1。系统由AM 电机（auxiliary motor）匹配2 挡行星排变速器后再与TM电机（traction motor）同轴耦合后组成，构型简图见图2。2 挡行星排变速器由换挡执行机构、双锥环同步器、单行星排齿轮组成，基本结构见图3。

图1 双电机耦合高效电驱动系统应用场景

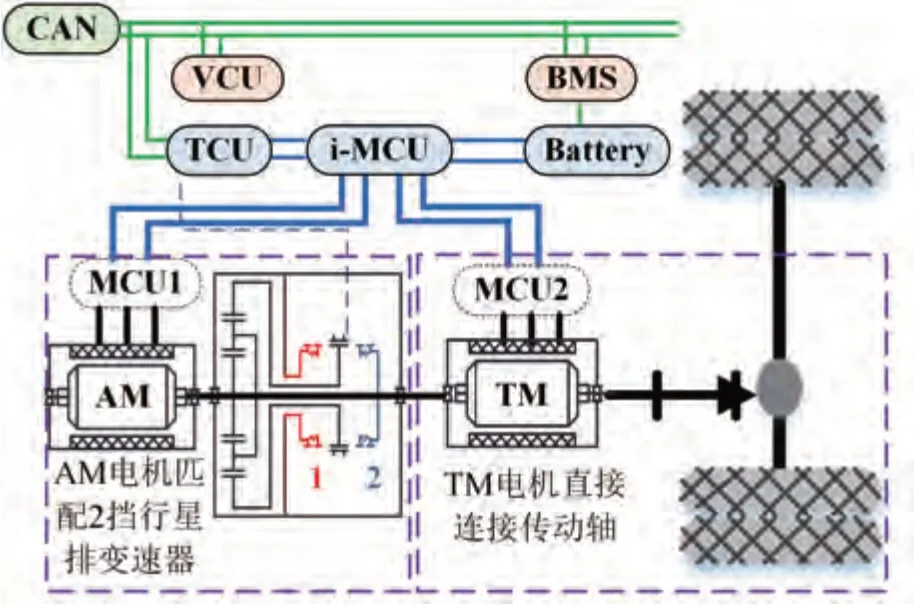
图2 双电机耦合高效电驱动系统构型简图

图3中“1”为换挡电机；“2”为换挡指（拨动换挡拨叉）；“3”为换挡螺母；“4”为换挡丝杠；“5”为结合套；“6”为外锥环；“7”为内锥环；“8”为1 挡结合齿；“9”为2 挡结合齿；“10”为行星轮；“11”为行星架；“12”为太阳轮；“13”为齿圈。行星排变速器的基本工作原理是图3 中的换挡电机1 与换挡丝杠4 一起做周向旋转，推动换挡螺母3 沿轴向运动，带动换挡指2 周向旋转，换挡指2 推动换挡拨叉轴向运动，从而推动同步器结合套5 沿着轴向运动，实现摘挡、挂挡等动作。

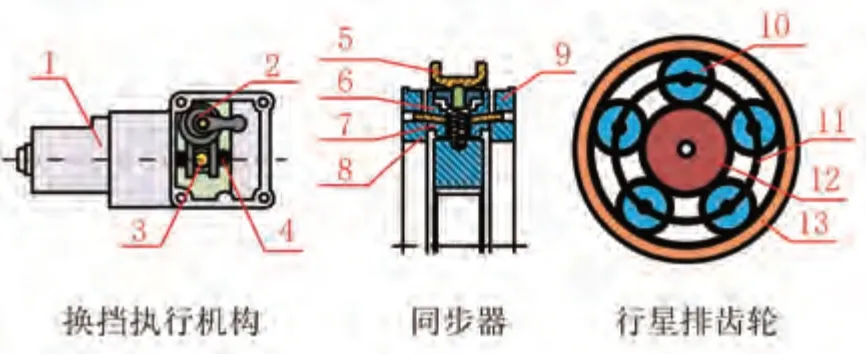
图3 两挡行星排变速器组成图

本文中研究的动力系统在原理样机开发完成后进行了402 h的可靠性耐久动态换挡实验，累计完成25 万余次换挡，分析了实验过程中的换挡位置数据，得到了如图4所示的换挡位置变化趋势。

从图4 可以看出，随着实验的进行，换挡机构产生了磨损使得各挡位的标定位置值发生了变化：1挡标定位置值变小，2 挡标定位置值变大，二者的差值有“外扩”的趋势。实验结束后，对变速器进行了拆解分析，拆解情况见图5。图中①为换挡指与同步器拨叉的接合部分，该部分没有明显的磨损；图中②为换挡指的“U”形槽，该部分与图中的③接合，从图中可以看出，②部分磨损比较严重，这是导致挡位标定位置值变化的主要原因；图中③部分为丝杠螺母两侧的圆柱部分，该部分与图中的②接合，从图中可以看出，该部分没有明显磨损。

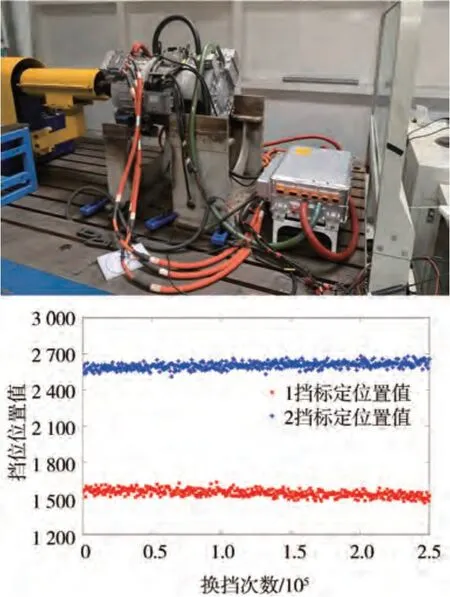
图4 换挡实验台架及换挡位置数据分析

图5 换挡执行机构拆解图

根据实验数据和拆解结果分析，随着时间的推移，换挡位置值发生了变化，这是因为磨损导致的结构参数变化引起的结果，结构参数的变化一方面会引入换挡位置的测量误差影响换挡，另一方面会影响控制模型的精度，使得换挡控制策略的鲁棒性变差，因此在变速器使用的过程中非常有必要对换挡执行机构的参数进行辨识，修正控制模型保持其精度。

1.2 换挡执行机构的数学模型

本文研究换挡执行机构的实物图及对应的简图见图6。

图6 换挡执行机构实物及简图

换挡执行机构的电机为直流有刷电机，其数学模型为式中：，，分别为换挡电机电流、换挡电机转速、换挡指转过的角度，可以直接或间接测量；，，，分别为直流电机电阻、直流电机电感、换挡力臂1的有效长度、换挡力臂2 的有效长度；为直流电机输入电压；为直流电机电阻；为直流电机电感；为反电势系数；为电磁转矩系数；为直流电机转子的转动惯量；为丝杠的转动惯量；为螺母的质量；为丝杠的导程；为进给丝杠的正效率；为换挡指等效到回转中心上的惯量；为同步器作用在换挡指上的负载力，这个力无法直接测量，后续模型简化过程中将该变量列为系统噪声。

如式（1）所示，换挡执行机构的数学模型具有高度非线性，无法直接进行参数辨识和状态估计。同时，为兼顾算法的效率和实时性，需要对模型进行适当简化。

换挡指转过的角度α 与电机的转速存在如下简化关系：

将上式2阶泰勒展开：

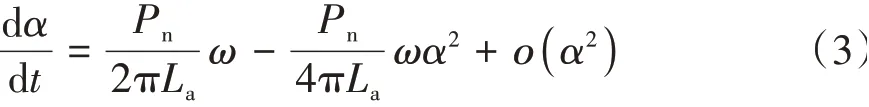
则换挡机构的系统方程可以简化为如下形式：

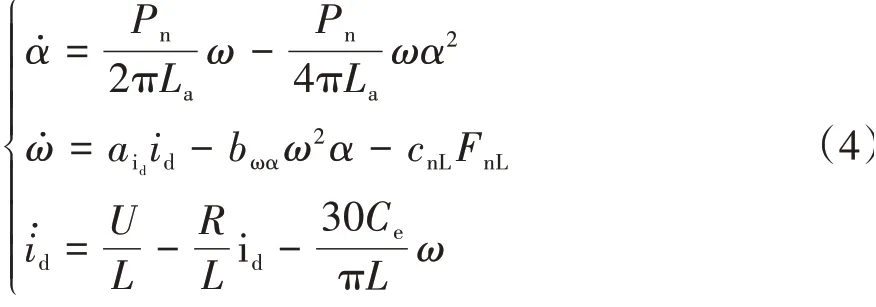
定义阻力矩：

通常情况下′与换挡机构的所在的位置（换挡指的角度）、变速器输入/输出轴的转速差Δ和输出轴的转速变化率˙相关，′可以写成如下形式：

换挡执行机构的系统方程可进一步简化为

式中：，均是只与相关的系数；是与和相关的参数。

2 基于DNHIF 算法的分层状态估计及参数辨识方法

换挡执行机构的系统方程可用下面的非线性时间连续的状态空间方程表述：

式中：为系统状态向量；为系统参数向量；为系统控制输入向量；为系统输出向量；为系统噪声向量；为系统测量噪声向量；为系统测量矩阵，在换挡执行机构的状态空间方程中，该矩阵为单位矩阵。

在变速器使用的全生命周期内换挡执行机构主要存在2个部分的磨损，一个是换挡指的“U”型槽部分的结构，该部分直接影响结构参数，另一个是推动同步器移动的结构，该部分直接影响结构参数，根据试验样机的拆解结果可以看出，“U”型槽的磨损及形变最为严重；其与同步器接合部分磨损程度相对较轻。因此，进行结构参数辨识时主要辨识的值。另外，本文研究的换挡电机为直流有刷电机，在进行执行机构参数辨识时假定电感不变，主要对电机电阻进行辨识。

在本文中进行如下定义：

式中：为需要估计的状态量；为需要辨识的参数。(，，)的具体表达式为

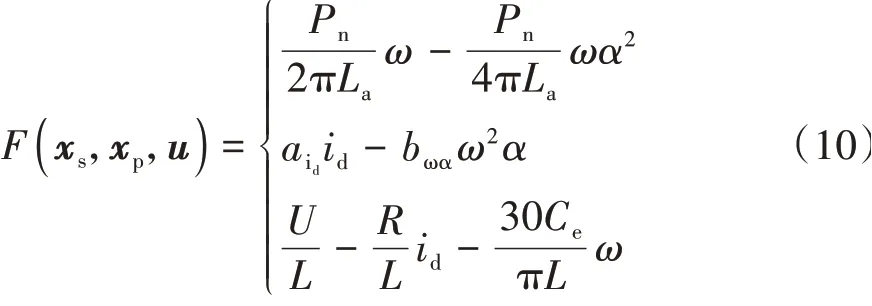
在实际的使用过程中，需要对模型进行离散化处理，系统的状态空间方程可以改写为

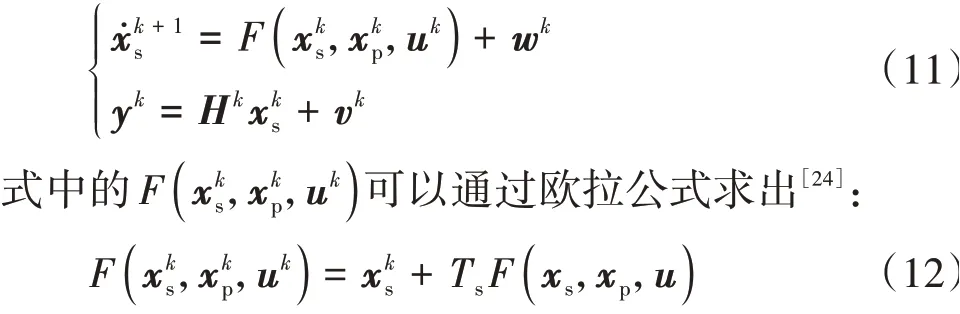
由式（10）可知系统需要估计的状态和待辨识的参数高度非线性耦合，在辨识系统参数时，为得到更加准确的结果，需要知道精确的系统状态信息，虽然角度和电流可直接量测得到，角速度˙可以间接得到，但是这些量测到的状态量往往含有干扰噪声，需要进行滤波后才能使用，使用比较广泛的估计算法是卡尔曼滤波算法（Kalman filter，KF），但是对于本文模型的高度非线性化以及噪声特性的未知导致了卡尔曼滤波不再适用。文献［26］中采用HIF 算法来解决这类问题。本文将基于NHIF 算法设计一种分层状态估计和参数辨识的方法（DNHIF）来实现模型高度非线性、噪声特性未知情况下的状态估计（，，）和参数辨识（，）。具体的分层状态估计和参数辨识方法原理见图7。

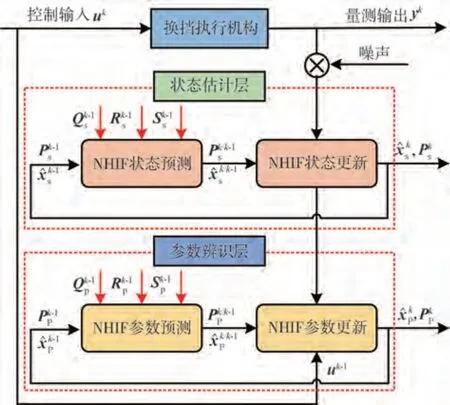
图7 DNHIF分层状态估计和参数辨识方法原理图

下文将分别对状态估计层和参数辨识层的估计器进行设计。

2.1 基于NHIF算法的执行机构状态估计器设计

基于NHIF 算法估计换挡执行机构的状态^=[]，列出线性化后的相关状态空间方程：

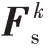
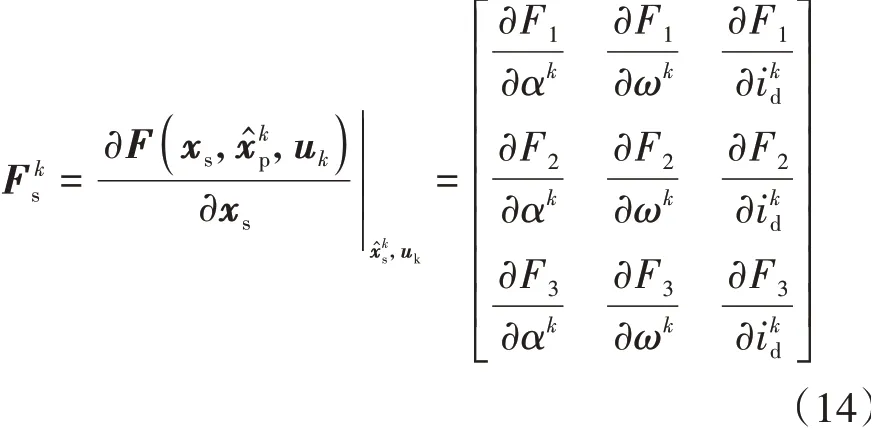
图8 执行机构状态估计算法流程图

2.2 基于NHIF算法的执行机构参数辨识器设计

在进行系统参数辨识时，需要重新改写系统方程，将待辨识的=[]参数作为系统的状态量，并且假定为随机游走，系统的待辨识参数具有如下特性：

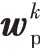
由于系统的参数不可直接测量，这里将状态估计器估计得到的执行机构的状态定义为量测量，这样处理的依据是使用系统的方程作为量测方程，系统的量测方程定义如下：

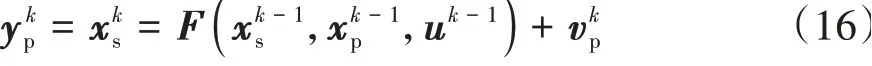
系统的线性化状态空间方程可以改写为如下形式：

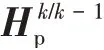
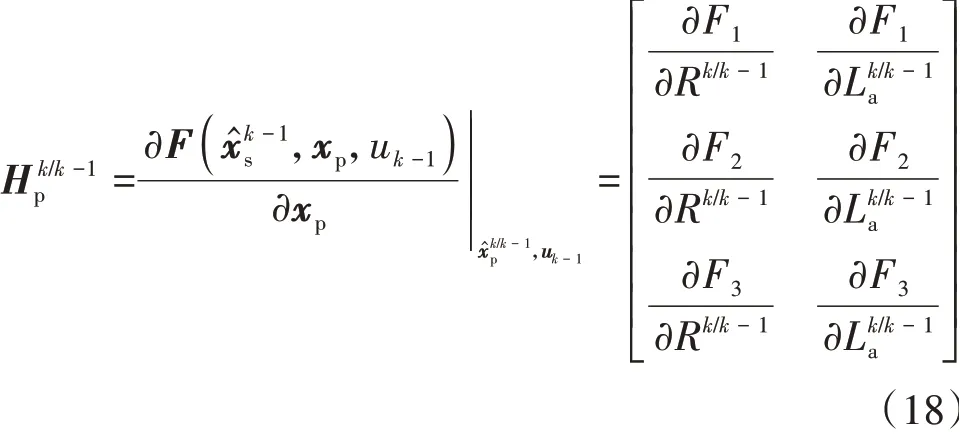
图9 执行机构参数辨识算法流程图

2.3 基于DNHIF算法的分层状态估计器及参数辨识器设计

及参数辨识方法的流程图，采用这种方法对执行机构的状态和参数进行联合估计。上层状态估计器对执行机构状态进行估计，估计结果作为下层参数辨识器的量测量，下层参数辨识器使用系统方程作为量测方程，对执行机构的参数进行辨识，辨识结果为上层估计器提供模型参数。

3 实验验证

本文实验验证分为2 个部分，先通过实验验证本文提出的基于DNHIF 算法的状态估计及参数辨识方法的准确性和有效性，然后对比通过参数辨识修正系统模型参数对换挡性能的影响。

3.1 基于DNHIF方法的状态估计及参数辨识验证

本文设计了一种基于自动标定的参数辨识流程，见图11。在对因磨损导致的换挡位置标定值进行偏差修正的同时验证本文提出的基于DNHIF 算法的分层状态估计和参数辨识方法的有效性。量测数据来自变速器的自动标定过程。

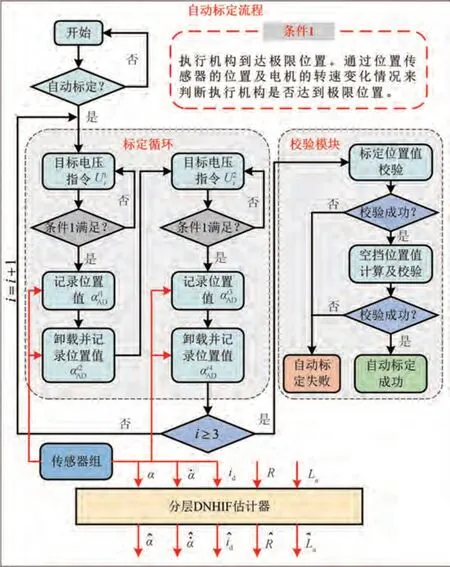
图11 基于自动标定的参数辨识流程

本节基于实验台架对提出的基于DNHIF 算法的分层状态估计和参数辨识方法进行验证，实验台架见图12，机构的基本参数见表1。根据实际情况，在实验的过程中，将待辨识的参数的初始值设定在真实值的50%～150%的范围内，将高斯噪声注入到量测量上。

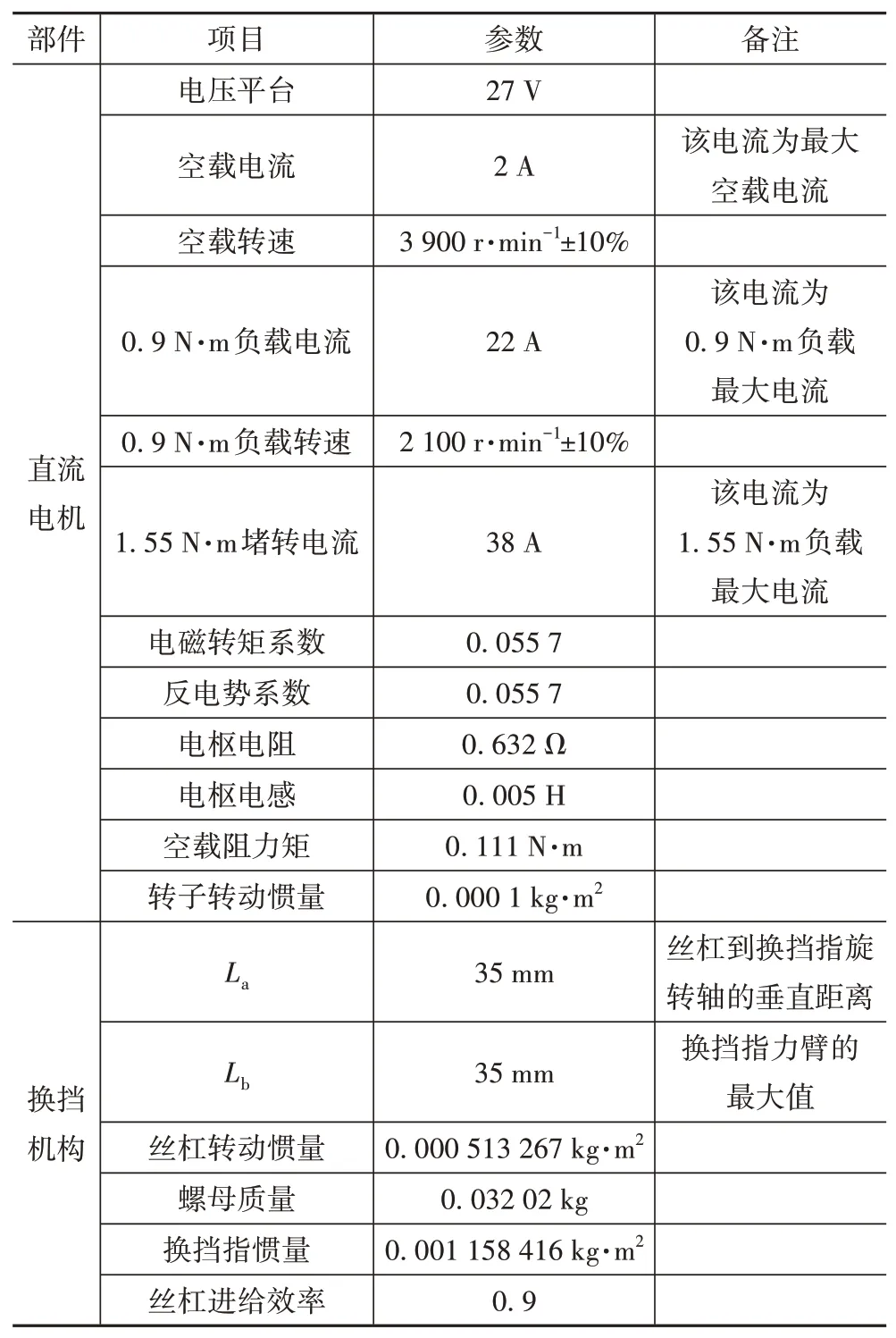
表1 换挡执行机构基本参数

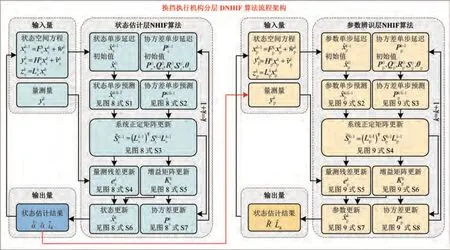
图10 分层状态估计器及参数辨识算法流程

图12 实验台架

实验结果如图13 所示。从图13（a）和图13（b）可以看出，本文提出的DHIF算法能够比较准确地估计直流电机转速和换挡位移，几乎不存在偏差。如图13（c）在整个过程中直流电流基本也能比较准确地被估计出来，但是在250 和700 ms（图中标注的地方）左右估计的电流值和参考值存在一定偏差，分析可能的原因是接近目标挡位时同步器与目标挡位齿轮发生了碰撞导致负载发生了突变，而在系统模型中负载被当作未知噪声影响了模型精度，从而使得电流估计结果产生了小范围偏差。

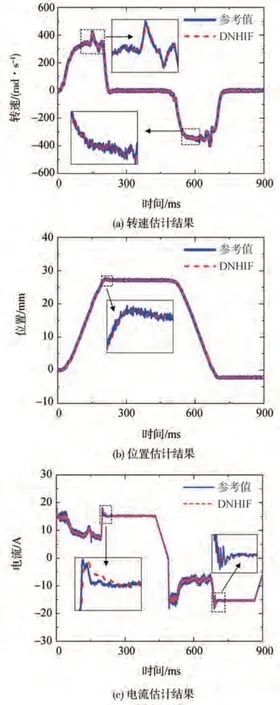
图13 执行机构状态估计结果

图14（a）和图14（b）展示了执行机构参数辨识的结果。图14（a）中，在动态过程中（0～200、500～700 ms 时间段内）换挡电机的电阻参数辨识结果存在一定的偏差，堵转过程（200～500、700～900 ms 时间段内）中的辨识比较准确。分析可能的原因是将负载当作噪声对系统模型进行简化影响了模型精度，导致动态过程中的辨识结果出现了偏差。由于直流电机的电压和电流可以直接测量，在电机堵转过程中，通过电路模型就可以准确地将直流电机的电阻辨识出来。图14（b）展示了换挡力臂的辨识结果，从图中可以看出DNHIF 估计器花了600 ms 左右使得换挡力臂收敛到参考值附近，稳态误差比较小，分析收敛时间比较慢一方面是模型精度的引起的，另一方面是DNHIF 估计器本身的特性导致的。但总体来讲，从实验结果可以看出本文提出的DNHIF算法在执行机构的状态估计和参数辨识方面表现出了较高的准确性和可靠性。

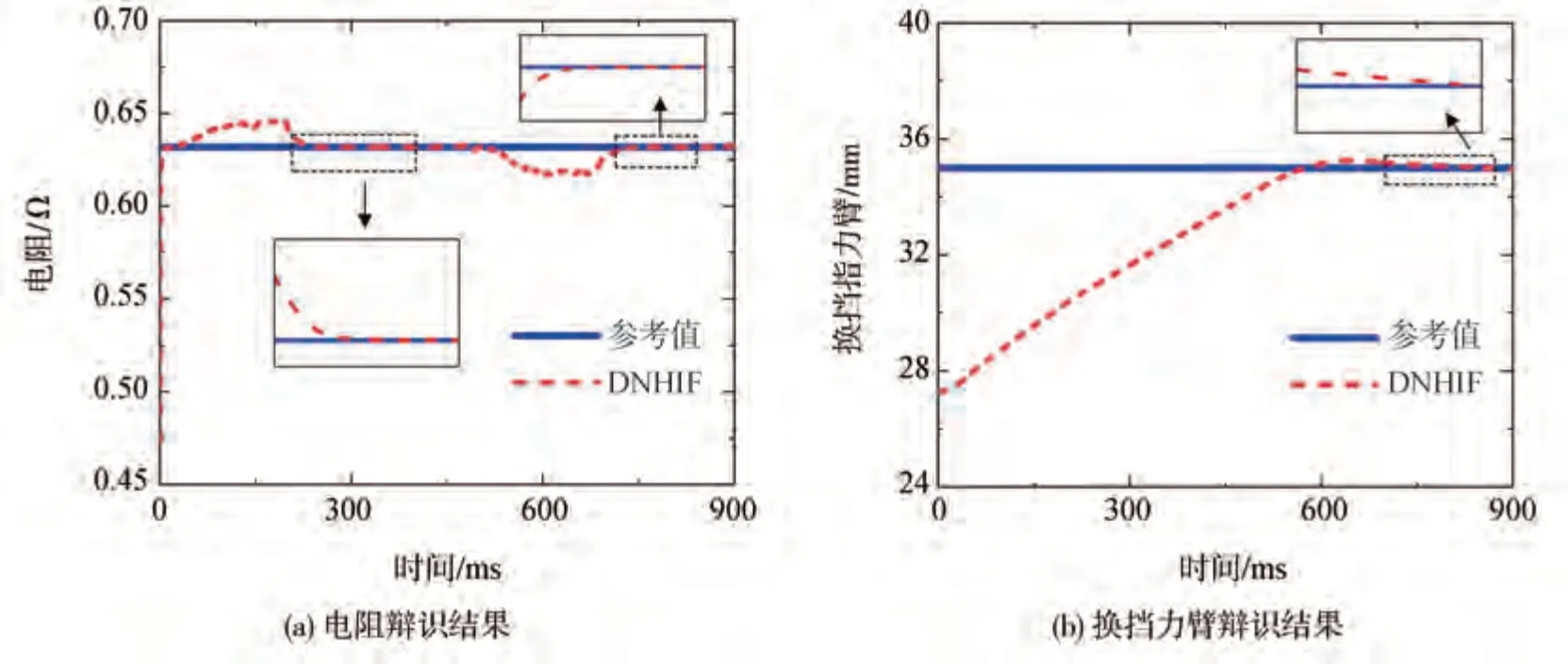
图14 执行机构参数辨识结果

为验证本文提出的基于DNHIF 算法的换挡执行机构状态估计和参数辨识方法的鲁棒性及准确性，将其与基于DEKF（Dual-EKF）算法的联合辨识方法进行了对比验证。图15（a）、图15（c）、图15（e）分别给出了换挡电机转速、换挡位移、直流电机电流的对比估计结果，图15（b）、图15（d）、图15（f）分别给出了各自的平均绝对误差（MAE）统计。从实验结果可以看出，在对直流电机转速和换挡位移进行估计时2 种算法都表现出了相当的准确性，但基于DEKF 算法的MAE 比基于DNHIF 算法大。但在对直流电机电流进行估计时，2 种算法表现出了很大的差异性，基于DNHIF 算法的准确性要明显高于DEKF算法。

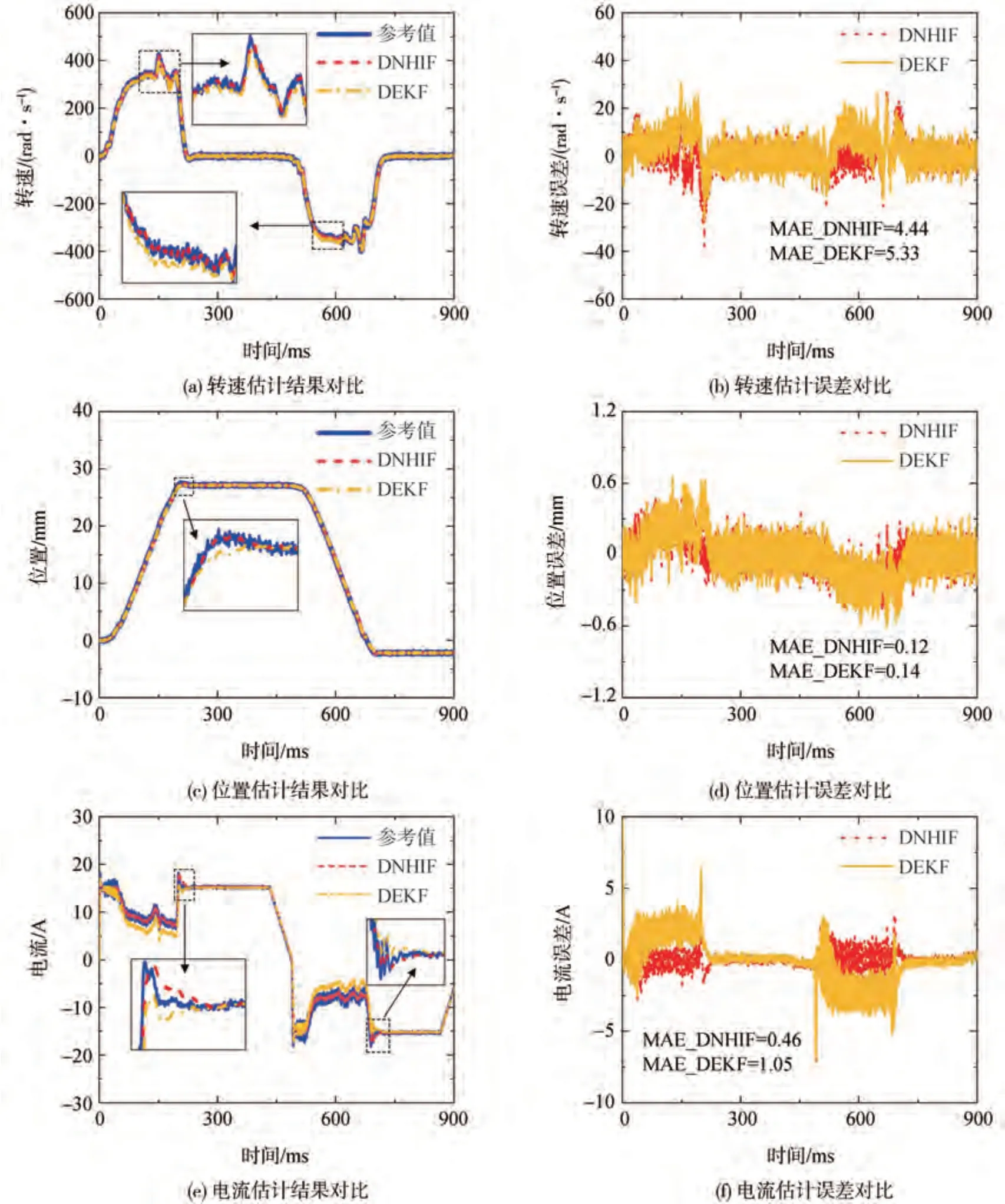
图15 执行机构状态估计对比结果

图16（a）、图16（c）展示了基于DNHIF 和基于DEKF 算法的执行机构参数辨识对比结果。如图16（a）所示，在辨识换挡电机电阻方面，2种算法都表现出了一定的准确性，但是受限于EKF 算法对模型和噪声的要求，基于DEKF 算法的估计结果的稳态误差要比基于DNHIF 算法的大。这种在稳态误差方面的差别在对换挡力臂的辨识上体现的尤为明显，如图16（c）所示，虽然收敛过程慢，但基于DNHIF 算法辨识的换挡力臂的稳态误差要明显小于DEKF 算法。由于收敛速度及初值设定的问题导致了基于DNHIF 算法对换挡力臂辨识结果的MAE 要比基于DEKF 算法的大。DNHIF 算法和DEKF 算法对换挡执行机构状态估计和参数辨识的误差统计见表2。相比DEKF算法，DNHIF算法对电机转速估计的平均绝对误差降低了16.7%，换挡位移估计平均绝对误差降低了14.3%，电机电流估计平均绝对误差降低了56.2%，电机电阻估计平均绝对误差降低了55.6%，但换挡力臂的平均绝对误差增加了227%，需要说明的是，基于DNHIF 算法辨识换挡力臂的误差大是因为初值设定问题和算法运算量的问题导致了收敛速度比较慢，但是最终的稳态误差要比DEKF 算法的误差小。总体来讲，实验结果表明了基于DNHIF 算法的状态估计及参数辨识方法的准确性和有效性.

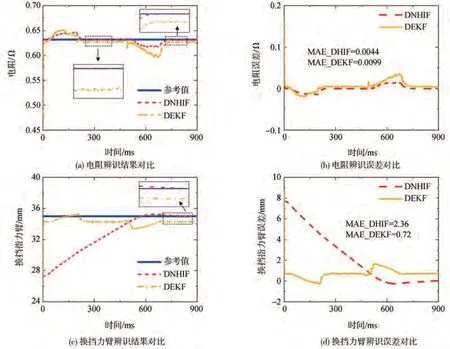
图16 执行机构参数辨识对比结果

表2 不同算法状态估计和参数辨识MAE值

3.2 修正换挡执行机构参数对换挡性能的影响

本节通过实验验证了是否修正换挡执行机构参数对换挡性能的影响，由于换挡是在室温条件下进行，实验过程中主要进行修正结构参数（换挡力臂）的对比实验，实验结果见图17。在进行402 h 的动态换挡实验后，换挡执行机构结构参数发生了变化，在没有修正该参数时进行了换挡实验，实验结果见图17（a）。从图17（a）可以看出，摘挡过程中的换挡位移跟踪存在超调和振荡，整体摘挡时间大约450 ms。挂挡过程的整体挂挡时间大约300 ms。图17（a）中的控制指令也出现了抖动。采用本文提出的方法对换挡执行机构的结构参数进行修正后进行了对比换挡实验，从图17（b）可以看出，在摘挡和挂挡过程中，换挡位移的跟踪效果良好，摘挡过程持续了230 ms 左右，挂挡过程持续了200 ms 左右。实验过程的具体数据对比见表3。

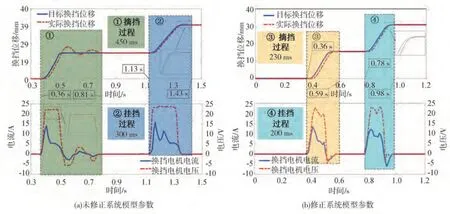
图17 系统模型参数对换挡性能的影响

表3 修正模型参数和未修正模型参数换挡过程数据统计表

从对比实验可以得出，修正换挡执行机构参数对换挡性能的提升至关重要，不进行参数修正会使得换挡过程中的目标位移跟踪出现超调振荡，不仅会使整体换挡时间增加，甚至会导致换挡失败的情况。

4 结论

通过台架实验发现了变速器换挡执行机构参数存在时变的问题，结构参数的时变一方面增加了系统状态的量测误差，另一方面使得控制策略的鲁棒性变差影响换挡性能。在考虑系统模型高度非线性、系统噪声特性未知的情况下，提出了一种基于DNHIF 算法的分层状态估计和参数辨识方法，对换挡执行机构进行状态估计和参数辨识。状态估计和参数辨识均采用NHIF 算法，根据NHIF 算法对噪声未知性无强制约束的特点，将状态估计和参数辨识过程中的负载列为扰动噪声简化了模型。

实验结果表明，本文中提出的基于DNHIF 算法的状态估计和参数辨识方法具有较高的稳定性和准确性，状态估计结果几乎无偏差，辨识结果的稳态误差比较小。通过实验对比，修正系统模型参数后换挡性能得到了明显改善。

本文提出的方法在系统模型高度非线性化、系统噪声特性未知的情况下仍能对系统模型参数进行辨识，对系统状态进行准确估计，进一步改善了系统的控制性能，该方法也可以推广到模型非线性、复杂程度较高，系统噪声特性未知的系统上。