跟驰场景中网联混合电动货车速度规划和能量管理协同控制的研究*
解少博,屈鹏程,李嘉诚,王惠庆,郎 昆
(长安大学汽车学院,西安 710064)
前言
货车具有较大的迎风面积,在行驶中空气阻力消耗的能量占总能耗的比重十分显著,而编队行驶可以通过对车速进行精准控制来调节车间距,改善前车和跟驰车辆的空气流场形态,达到降低空气阻力的目的。编队行驶已被证实是提升经济性的有效手段之一。对配置有发动机和电池的混合动力货车(HET),为了进一步提升经济性,除了通过编队行驶降低能耗,还可以优化能量源之间的功率分配关系达到节能目的,即优化能量管理策略。与此同时,由于电池成本在HET 总成本中占有很大比重,能量管理策略所决策的电池输出功率除了影响整车的能耗经济性,还影响到电池老化速率及对应的老化成本。显然,更多地使用电池的电能尽管可以提升能耗经济性,但会增大电池的老化成本。因此,从整体经济性来考虑,须协同考虑电池的老化成本和功率分配来优化能量管理策略。
另一方面,HET 在队列中的跟驰速度影响到与前车的车间距,从而影响到行驶的安全性和空气阻力,同时跟驰速度还决定了功率需求,而HET 的能量分配关系又决定了电池的输出功率,从而影响到整车的能耗成本和电池老化成本。由此可见,处于跟驰场景中的HET,速度规划和能量管理两个决策行为是互相关联的,且影响到跟驰安全性、能耗经济性、电池老化和空气动力效应等多个性能。
针对燃油汽车编队行驶的节能策略已展开了相关研究,针对新能源汽车的编队控制也已引起关注。文献[5]中针对红绿灯场景下兼顾车间协同控制和燃油经济性,提出分层模型预测控制策略,上层从优化速度和舒适性等角度获取最优经济车速,下层实施能量管理策略优化动力源输出,实现了车队通过红绿灯的协同控制。文献[6]中针对混合动力货车的空气阻力、速度规划和能量管理问题,提出集成协同优化策略,进一步降低了能耗。
电池作为电动汽车的重要零部件,合理地使用电池对于提升整车经济性意义重大。为了提升安全性和经济性等性能,需要从全局视角理清货车在跟驰过程中电池老化与其他目标之间的耦合关系。现有研究针对跟驰过程中空气阻力的优化以及混合动力车辆的能量分配均有涉及,而针对新能源汽车在跟驰过程中协同考虑跟驰安全性、空气阻力、能耗成本以及电池老化等多重目标的速度规划和能量管理协同控制问题尚未给予重视。
基于上述考虑,本文中针对网联HET 在跟驰过程中的速度规划和能量管理协同控制问题,提出一种综合考虑安全性、能耗经济性、空气阻力和电池老化等多重目标的协同模型预测控制(CMPC)策略。它基于模型预测控制的架构,在滚动时域内利用动态规划进行多重目标的优化,开发实时性协同控制策略。
1 车辆系统模型
1.1 动力系统结构
本文中假设跟驰场景中的HET 的动力系统结构如图1 所示。柴油发动机和发电机(ISG 电机)机械连接组成EGU 单元,EGU 单元和动力电池电力耦合,提供车辆行驶的功率需求和能量回收。表1 为整车主要参数。

图1 HET动力系统结构
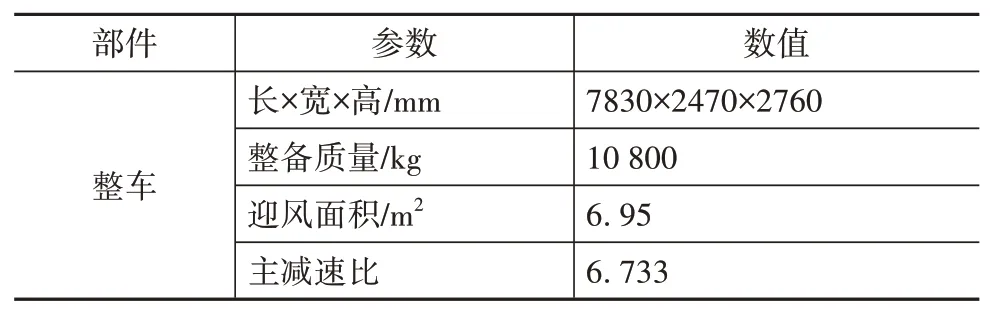
表1 整车主要参数
1.2 动力系统模型
1.2.1 动力部件模型
对于发动机和电机,基于稳态试验数据可以将其能耗效率表示为转速和转矩的函数,它们的能耗效率MAP图如图2~图4所示。

图2 发动机燃油消耗特性图
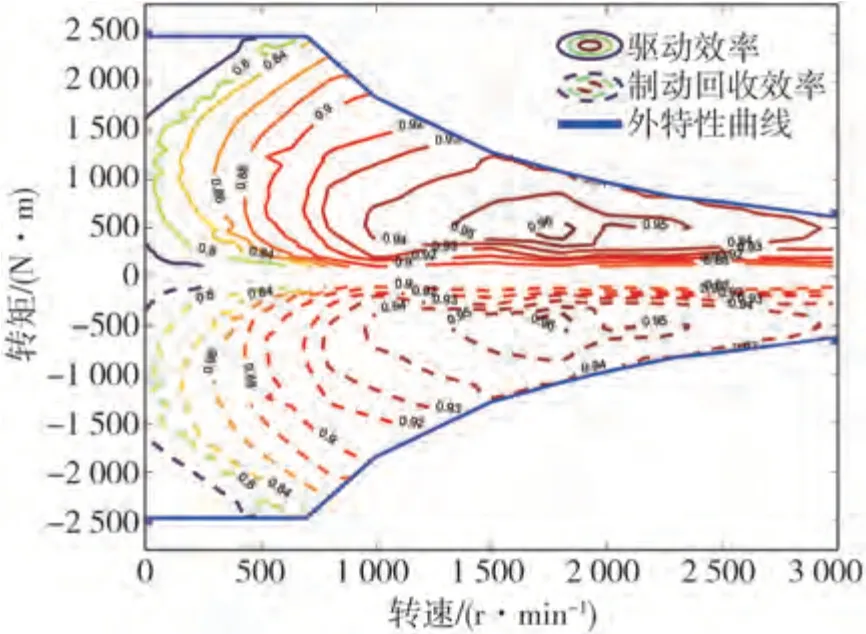
图4 驱动电机效率MAP图
1.2.2 电池模型
动力电池类型为磷酸铁锂电池,电池组由156个单体串联而成,每个单体容量为60 A·h,电压为3.2 V,电池组的总电压为499.2 V。

图3 ISG电机效率MAP图
1.3 车辆跟驰动力学模型
1.3.1 跟驰模型
为了保证车辆在跟驰时的安全性,避免追尾事故,定义最小车间距为

式中:为最小跟驰车间距;c为常量,表示停车时必要的车间距,取值1 m;为制动器响应时间,取值为0.5 s;为车辆在跟驰行驶时后车的速度。
同时,过大的车间距会影响道路通行效率,而且会引起其他车辆的插入,影响车队的跟驰安全性和队列的完整性,还会极大降低减阻效应。因此定义最大车间距为

式中:为最大跟驰车间距;为常量,取值为1.5 m;为标定系数,取值为0.8;Δ为离散时间步长,取值为1 s。
期望车间距是为跟驰车辆的速度规划提供参考,使车辆的安全性得到保障并降低空气阻力。基于车头时距的期望车间距模型可表达为

式中:为停车后的期望车间距;()表示车头时距,是的函数,当()为常数时该公式表示恒定车头时距模型,否则为可变车头时距模型;和均为取值是正数的标定系数,单位分别为s/m和s。
1.3.2 减阻效应模型
本文中应用XFlow软件对车辆在跟驰过程中空气阻力系数的变化进行仿真研究。在XFlow软件中设置计算域的长、宽、高分别为80、16和30 m,湍流和汽车表面的解析度为0.012 5 m,气流设定以恒定值25 m/s由入口垂直进入,同时设置不同的车间距并记录空气阻力系数。图5为最终拟合得到的跟驰车辆空气阻力系数与非跟驰时的空气阻力比值随车间距的变化曲线。

图5 空气阻力系数比值随车间距的变化轨迹
1.4 电池老化模型
本文的电池容量衰减模型可描述为

式中:为电池容量损失百分比;为指数前因子;为活化能;为充放电倍率;为气体常数;为电池温度;为指数因子;为安时吞吐量,即电池充放电电流绝对值对时间的积分;和为标定系数。
考虑=20%时电池寿命终止。在计算过程中,忽略各单体电池间的差异,电池瞬时老化成本计算公式为

式中:为电池瞬时老化成本;为车辆当前行驶时刻;为单位电量电池组购置成本;为电池组总电量;为电池组总容量;为电池单体瞬时容量衰减程度;为电池工作环境温度;为电池电流;为电池容量衰减因子,定义为标准工况与实际工况下电池总安时吞吐量的比值;为电池组串联单体数;为标准试验工况下,电池寿命终止前的总安时吞吐量;为单体中并联的电芯数。
2 跟驰场景HET多目标协同控制问题
为了实现实时性控制,基于模型预测控制的思想在滚动时域内构建目标函数。基于模型预测控制提出考虑空气动力效应的协同控制策略,后文简称CMPC 策略,其原理如图6 所示。另外,本文中假设后车可以通过V2V 通信实时获取前车的车速信息和车间距信息。

图6 CMPC策略执行流程图
2.1 目标函数构建
在构建目标函数时,首先量化安全性成本、能耗成本和电池老化成本。
2.1.1 安全性成本
货车在跟驰过程中,首先要保证与前车的安全性,即货车之间不能发生碰撞或存在发生碰撞的隐患,而且后车要能随时捕捉到前车的位置信息,保证车队的完整性;在此基础上考虑经济性优化问题的求解。因此前车和跟驰车辆的车间距必须大于最小车间距,并尽可能接近期望车间距。为了量化安全性,根据建立的纵向动力学模型,定义安全性成本为

式中:为行驶安全性成本;、和为权重常量,其取值分别为2 元/m、5 元/m和40 元/m;为预测时域内的时刻;为实际车间距。
2.1.2 经济性成本
本文的HET 具有EGU 和动力电池两个动力源,并且考虑到电池老化成本,定义经济性成本为电耗成本、电池老化成本和油耗成本之和:

式中:为经济性成本;和分别为柴油单价和电价,取值分别为6.5元/L和1.0元/(kW·h);˙为发动机燃油消耗率;为电池功率消耗。
2.1.3 目标函数
考虑到安全性成本和经济性成本量纲及数量等级的不同,以滚动时域内的经济性成本和等效安全性成本的加权和最小化构建目标函数:

式中:为综合评价指标;为车辆当前行驶时刻;为预测时域长度;为经济性成本的权重因子,根据仿真测试取为无量纲常数1 400。
2.2 目标函数的求解-MPC
针对滚动时域内的优化问题,采用DP 进行求解。其中,选择货车加速度和EGU 输出功率作为控制变量,动力电池SOC和车速为状态变量,对控制变量优化求解。同时,假设在预测时域内后车具有恒定的加速度。
2.3 滚动时域的模型预测
在计算后车安全性成本时,须在滚动时域内对前、后车的车速进行预测。对于前车,采用长短时记忆神经网络(LSTM)进行滚动时域内的车速预测;后车则采用CMPC策略预测车速。
图7为实车采集得到的前车历史车速谱,工况No.1、No.2、No.3 和No.4 用于对LSTM 神经网络训练,将No. 5 用于仿真验证。表2 列出了LSTM 网络在不同预测时域长度时的预测精度。

图7 历史车速谱

表2 不同时域长度的预测精度
从表中可以看出,预测精度随着预测时域长度的增加逐渐降低,但预测时域越短,经济性优化效果会越差,故综合考虑优化效果、预测精度和时间效率,选择3 s作为预测时域长度。
3 人工跟驰模型
为了对提出的CMPC 策略进行评估,基于一种反映人工驾驶的速度跟驰模型—全速差耦合模型(full velocity difference coupled model,FVDCM)进行比较。对于HET 的能量分配,分别选择基于规则的电量维持策略(CS)和基于全局优化的庞特里亚金最小值原理(PMP)进行仿真分析和结果对比。
3.1 FVDCM模型
在FVDCM 模型中,前车的状态变化过程可以表示为

式中:和分别为前车的车速和加速度;为前车的行驶距离信息;Δ为采样时间。
后车的状态变化可以描述为

式中:表示驾驶员的反应灵敏度;Δ为前车与后车的速度差;表示驾驶员对Δ的敏感度;为采样间隔,取值为1 s;表示跟驰车辆的最优车速函数,其具体定义可见文献[11]。
3.2 FVDCM+CS
基于规则的能量管理策略可通过设置合理的规则,使车辆驱动模式规律性切换以满足车辆行驶功率需求的同时降低能耗。CS 策略的SOC 下限设置为0.55,上限设置为0.65,EGU功率取恒定值70 kW。
3.3 FVDCM+PMP
与动态规划策略相比,PMP 在设计能量管理策略时具有与动态规划相近的优化结果,但其计算效率更高。为此,进一步采用PMP 将能耗最优问题转化为含约束的非线性优化问题,并通过打靶法获得EGU和动力电池的最优功率分配序列。
4 结果与分析
本文中以No.5速度谱(见图7)来模拟跟驰过程中前车的车速,并假设HET(后车)在整个行程中一直处于跟驰状态,不考虑后车和前车的分割以及外来车辆在两车间的插入等情况。
以No.5速度谱为例(里程为58.8 km)进行仿真行驶,电池SOC 初始状态为0.60。电池寿命衰减模型的相关参数:气体常数为8.314 J·mol·K,环境温度为298.15 K,指数前因子为31 630,指数因子为0.55,系数和分别为-31 700和370.3,电池购置成本设为1 500元/(kW·h)。
4.1 目标函数考虑电池老化与否的比较
为分析电池老化这一因素对经济性成本的影响,对比在目标函数中考虑电池老化成本与否时的结果。因此,期望车间距设定为固定值18 m。结果如表3 所示,其中,CMPC-bc-w/o 表示目标函数中不考虑电池老化的策略,CMPC-bc-w 表示目标函数中考虑电池老化的策略,经济性成本为电池老化成本与能耗成本之和。

表3 目标函数中考虑电池老化成本与否的结果对比
由结果可知,与目标函数中不考虑电池老化相比,考虑电池老化的经济性成本在整个行程降低了1.90%。其原因是由于CMPC-bc-w 策略抑制了电池的大电流放电过程,因此在总需求功率不变时,油耗量和电耗量变化不显著,但可以抑制电池大电流放电有助于降低电池老化速率,减少老化成本,从而使CMPC-bc-w的经济性成本下降。
图8为两种策略下动力电池的充放电倍率变化曲线。可以看到,CMPC-bc-w 的充放电倍率明显低于CMPC-bc-w/o。

图8 充放电倍率对比
图9是两种策略的动力电池SOC对比,可以看出,与CMPC-bc-w/o 策略相比,CMPC-bc-w 策略的SOC轨迹波动范围较小。图10是速度对比图,图11是车间距对比图。可以看出,CMPC-bc-w策略的跟驰车间距变化范围更窄,车辆在跟驰行驶过程中货车之间的车间距更稳定。因此,CMPC-bc-w策略是对CMPC-bcw/o策略的进一步优化,从经济性和跟驰安全性两个方面来看,CMPC-bc-w策略均具有更优的控制效果。
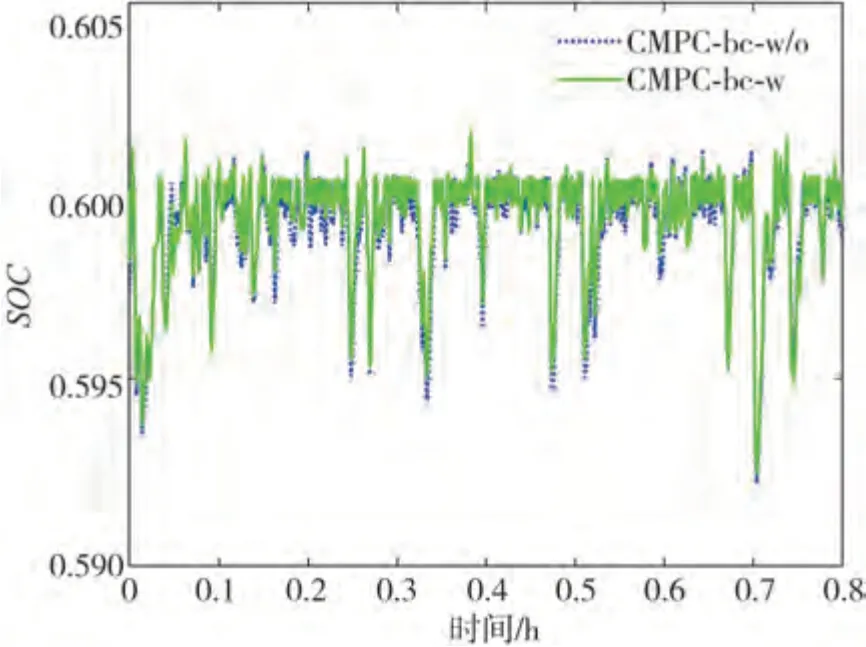
图9 SOC轨迹

图10 实际车速变化曲线

图11 实际车间距变化曲线
4.2 考虑空气动力效应和电池老化与否的结果对比
为分析空气动力效应和电池寿命衰减两个因素耦合时的效果,对比目标函数中同时考虑这两种因素与不考虑这两种因素的结果。在这两种情况下,当目标函数中不考虑空气动力效应时,空气阻力取为恒定值,而当考虑空气动力效应时,期望车间距和空气阻力随车速变化。结果如表4 所示,其中,CMPC-w/o 表示目标函数不考虑空气动力效应和电池老化成本的策略,CMPC-w 表示目标函数同时考虑空气动力效应和电池老化成本的策略。

表4 目标函数中考虑空气动力效应和电池老化成本与否的结果对比
可以看出,CMPC-w 相比CMPC-w/o在整个里程的经济性成本降低15.11%。主要原因是抑制电池老化速度与动态调整车间距这两者的耦合作用,使能耗经济性明显提升。
两种策略的动力电池SOC 曲线如图12 所示,实际跟驰车间距如图13所示。

图12 SOC轨迹

图13 实际车间距变化曲线
从图中可以看出:与CMPC-w/o 策略相比,CMPC-w 策略的SOC 轨迹波动范围较小,电池充放电深度较浅,从而有效抑制了电池老化速率,降低了电池老化成本;另一方面,由于CMPC-w 策略的跟驰车间距更小,气动效应降低了车辆的总功率需求,致使驱动车辆的需求功率峰值有所削减。综上所述,目标函数中考虑空气动力效应和电池老化时,能够有效提高HET 的使用经济性。由结果还可以看出,相比考虑电池老化对HET 经济性的改善,考虑空气动力学效应对其经济性的提升效果更为显著。
4.3 CMPC协同控制策略性能评估
速度规划的目的是面向自动驾驶。为进一步对比协同控制策略与人工驾驶在不同跟车距离时经济性成本的差异,本节基于改进的全速差模型(FVDCM)并结合能量管理策略(包括基于规则的CS策略和基于全局优化的PMP 策略)与CMPC 协同控制策略进行对比分析。结果如表5 所示,其中,FVDCM+CS和FVDCM+PMP 分别表示基于改进的全速差驾驶模型与电池电量维持策略和基于改进的全速差模型与庞特里亚金最小值原理的全局策略。

表5 目标函数中考虑电池老化和空气动力效应与另外两种策略的结果对比
由表可知,CMPC 的经济性成本仅比FVDCMPMP 的经济性成本高1.07%,能耗成本高1.54%,但FVDCM-PMP 属于全局最优算法,不具备实时性。而与FVDCM+CS 相比,CMPC 的经济性成本则降低了14.37%,能耗成本降低了13.53%。由此可见协同控制策略在实时性和经济性方面的优势。
图14和图15 分别为FVDCM 和CMPC 两种跟驰模型的车间距和空阻系数的对比。可以看出,尽管FVDCM 和CMPC 的初始车间距都设为18 m,但前者的车间距基本维持在17~19 m 之间,波动范围较小。而CMPC为了提升经济性而柔性地调整车间距使其在10~14 m之间波动,即为了降低空气阻力并提升经济性而追求更激进的跟驰距离。由图15还可以看到,相比FVDCM策略,CMPC策略的后车空气阻力系数明显降低,因而能有效利用减阻效应实现节能行驶。

图14 不同策略车间距对比

图15 空气阻力系数对比
5 结论
本文中针对网联混合动力货车在跟驰场景中的速度规划和能量管理的协同控制展开研究,特别考虑了在跟驰行驶时的空气动力学效应和电池寿命衰减带来的影响,提出考虑跟驰行驶安全性、能耗经济性、空气动力学效应和电池老化的协同控制策略(CMPC)。与在目标函数中不考虑电池老化的策略对比,考虑电池寿命老化成本的协同控制策略降低了动力电池在高放电倍率下工作的频次,从而有效地降低了电池老化成本,在整个行程上的经济性成本降低了1.90%。与在目标函数中不考虑电池老化和空气动力效应的策略对比,考虑这两者的协同控制策略不但降低了动力电池在高放电倍率下工作的次数从而降低了电池老化成本,还有效利用空气动力学效应对货车跟驰距离进行优化,其经济性成本降低了15.11%。另外,与基于人工驾驶行为的跟驰模型进行对比,协同控制策略在实时性和优化效果方面具有更均衡的优势。

