线性回归分析技术在滴灌田间管网投资与建设规模影响分析中的应用

杜克余，魏辅婷，张文豪

（1.新疆天业（集团）有限公司，新疆 832000；2.国家节水灌溉工程技术研究中心（新疆），新疆 832000）

0 引 言

滴灌工程是一个系统工程，主要由水源工程、首部枢纽工程、田间管网工程及其附属设施组成[1]。田间管网工程投资是滴灌工程投资的重要组成部分之一，当田间管网工程的投资对工程建设规模比较敏感，其投资已成为滴灌工程总投资最重要的投资部分时，分析论证其经济规模范围内滴灌田间管网投资与建设规模的关系，可以为拟建工程项目投资预测提供非常重要的参考依据。线性回归是一类应用十分广泛的数据分析方法，可以确定两种或两种以上变量间相互依赖的定量关系。文章选取了不同建设规模的滴灌工程设计实例，分析滴灌田间管网投资对工程总投资的影响，从工程投资角度对工程造价影响较大的田间管网投资为研究对象进行分析，得出滴灌工程的经济规模，同时应用线性回归分析方法进行技术分析，通过回归建模，论证了滴灌田间管网投资与建设规模二者之间存在的相关性。由于方法简单可行，可以进一步为相关的节水灌溉工程投资分析提供借鉴作用。

1 工程实例选取及统计分析

1.1 工程实例选取

1.1.1 选取原则

根据以往施工的河水加压滴灌工程设计为实例，选取不同建设规模滴灌系统的基本原则：一是管网设计参数一致，种植模式及作物一致，灌水周期一致；二是管网管径计算运用经济流速法，支管管径选择按灌水小区允许压力偏差法进行计算[2]。

1.1.2 工程实例概况

本文选定新疆塔城地区小麦滴灌工程系统为研究对象，在以往施工的项目中抽取10 个不同建设规模的河水加压滴灌工程设计进行研究。主要工程量为滴灌首部系统10 个，沉淀池10 座，离心泵10 台，闸阀井、排水井807 座，埋设各种规格玻璃钢管道2 792 m，PVC 管道228 188 m；地面支管321 398 m，滴灌带18 410.2 km。预算单价采用当地建设工程造价信息，按照《新疆维吾尔自治区水利水电工程设计概（估）算编制规定》（新水建[2005]108 号）进行定额计价计算[2]。

1.2 数据统计分析

田间管网工程投资是滴灌工程总投资重要的投资部分，包括地埋管网工程、地面管网工程及其附属工程，主要内容为各类地埋管道、地面支管、滴灌带及闸阀井和排水井，经过计算得到田间管网工程的投资，并计算出单位面积投资，计算结果见表1,分析结果见图1、2。

表1 田间管网投资情况表

图1 单位面积田间管网投资与建设规模关系图

图2 田间管网投资比例与建设规模关系图

通过对表1 和图2 的分析得出，田间管网投资在总投资中占比较大，是主要投资部分；从图1 可以看出田间管网单位面积投资与建设规模的变化曲线呈现两边高、中间低现象，可知田间管网投资对建设规模较敏感[2]，另外在图1 中建设规模为68.33～137.67 hm2时，田间管网单位面积投资均位于8 300 元上下，且总体处于较低水平，可知此范围为经济规模，分析认为在建设规模为68.33～137.67 hm2时即经济规模范围内时，田间管网投资与建设规模二者之间存在某种线性关系。

2 线性回归分析及模型预测

为了进一步证实经济规模范围内田间管网投资与建设规模二者之间存在的线性关系，文章将通过线性回归分析的方法来论证。

2.1 基本公式

如果预测对象与主要影响因素之间存在线性关系，将预测对象作为因变量y,将主要影响因素作为自变量x，即引起因变量y 变化的变量，则它们之间的关系可以用一元线性回归关系式表示，见式（1）[3]，

式中，因变量y 为田间管网投资（单位：元），自变量x为建设规模（单位：hm2），a 和b 是揭示x 和y 之间关系的系数，a 为回归常数，b 为回归系数。

2.2 求解回归系数和回归常数

利用普通最小乘法原理(OLS)求出回归系数。最小二乘法基本原则是对于确定的方程，使观察值对估算值偏差的平方和最小。由此求得的回归系数见式（2），回归常数见式（3）[3]，

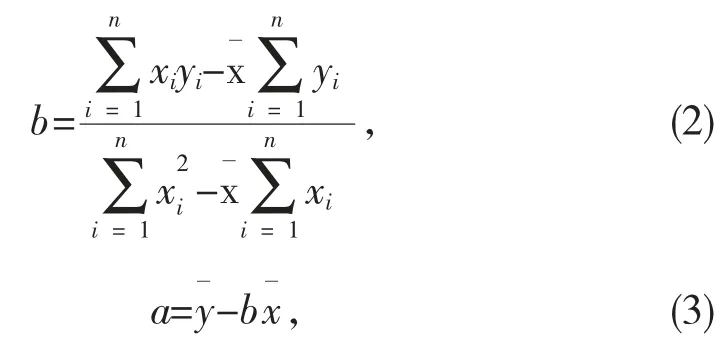
式中，xi、yi分別为自变量x¯和因変量y¯的观察值，和分別为x 和y 的平均值，分别见式(4)、式(5)，n 为样本数量。

经过前述统计分析，此处可选取建设规模为68.33～137.67 hm2时即经济规模范围内的数据作为观察数据，变量x、y 的观察数值xi、yi见表2，计算过程相关数据内容特征值，见表3。

表2 经济规模下田间管网投资情况表

将计算得出的相关数据内容特征值（表3）代入式（2）和式（3）中，计算得出回归系数b=7 913.46,回归常数a=42 708.46，初步得出一元线性回归关系式为y=42 708.46+7 913.46x。

2.3 回归检验

为了进一步判定预测模型的合理性和适应性，本文采用相关系数检验法对二者的一元线性回归关系式进行回归检验，检验基本公式见式（6），

式中：R 为相关系数，是描述两个变量x、y 之间的线性相关关系的密切程度的数量指标。

R 在-1 和1 之间，当R=1 时，变量x 和y 为完全正相关；当R=-1 时，变量x 和y 为完全负相关；当0＜R＜1 时，变量x 和y 为正相关；当-1＜R＜0 时，变量x 和y 为负相关；当R=0 时，变量x 和y 没有线性关系。所以R 的绝对值越接近1，表明其线性关系越好；反之，R 的绝对值越接近0，表明其线性关系越不好。只有当R 的绝对值达到一定程度时，才能采用线性回归模型进行预测[3]。

将计算得出的相关数据内容特征值（见表3）代入式（6）得出结果，R=0.993。

表3 回归分析计算过程相关数据内容特征值

经查相关系数临界值表，在自由度n-2 和显著性水平α(一般取α=0.05)下，R 临界值为0.878，即R0.05=0.878，可知R=0.993＞0.05，则变量x 和y 之间的线性关系成立。

综上可得出田间管网投资与建设规模二者之间的一元线性回归关系式，见式（7），

2.4 模型预测

2.4.1 点预测与区间预测

通过以上线性回归分析及检验得出回归模型后，就可以对相关实施案例进行预测，有点预测和区间预测之分。

点预测是在给定了自变量的未来值后，利用回归模型式(8)求出因变量的回归估计值，也称为点估计。

通常点预测的实际意义并不大，由于现实情况的变化和各种环境因素的影响，预测的实际值总会与预测值产生或大或小的偏移，如果仅根据一点的回归就做出预测结论，这是不科学的。因此预测不仅要得出点预测值，还要得出可能偏离的范围。于是，以一定的概率1-α 预测的y 在y'0附近变动的范围，称为区间预测[3]。

数理统计分析表明，对于预测值y'0而言，在小样本统计下(样本数据组n 小于30 时)，置信水平为100(1-α)%的预测区间为:

其中，t（α/2，n-2）可以查t 检验表得出。通常取显著性水平α=0.05。

2.4.2 田间管网投资的预测

如果要在本文工程实例的基础上用得出的回归关系式（7）预测相同地区建设规模为108.8 hm2的同类型滴灌工程田间管网的投资(单位：元),则预测过程及结果如下：

将x0=108.8 及经过计算得出的相关数据内容特征值（见表3）代入式（7），式（11），式（10）计算得出y'0=903 692.91，S0=31 420.35；然后通过查t 检验表得出显著性水平α=0.05 时t（0.025,3）=3.182；最后通过式（9）计算可得出在该地区建设规模为108.8 hm2的同类型滴灌工程田间管网的投资(单位：元)结果为：有95%的可能性在（803 713.37，1 003 672.45）的区间内。

3 结 语

本文应用线性回归分析的技术方法，分析了经济规模范围内滴灌田间管网投资与建设规模的相关性，进行了回归建模。研究表明，滴灌工程建设规模在68.33～137.67 hm2经济规模范围内时，田间管网投资与建设规模二者之间的线性相关性强。本文的研究，不仅可以为拟建工程项目投资预测提供非常重要的参考依据，还可帮助企业或相关管理部门将大量滴灌工程投资原始数据进行分析整理，科学可靠地为相关的节水灌溉工程投资分析提供借鉴作用。