基于测井参数的煤层含气量定量评价方法研究——以寿阳区块15#煤为例

李丹丹， 王振国， 降文萍， 张亚飞

(1.中煤科工集团西安研究院有限公司，西安 710077；2.中联煤层气有限责任公司，北京 100015)

煤层气是赋存在煤层中以甲烷为主要成分、以吸附在煤表面为主并部分游离于孔隙中或溶解于煤层水中的烃类气体[1]。我国煤层气资源丰富，开发煤层气具有获取清洁能源、促进煤矿安全生产、降低温室效应等多重效益。煤层含气量是表征煤储层特征的关键地质参数，是估算资源量、制定开发方案和产能数值模拟的重要依据，准确预测含气量对煤层气开发具有重要意义[2-4]。

目前，含气量直接测试方法为自然解吸法，测试精度高，但耗时长，成本较高[5]。测井是煤层气勘探开发中的重要测试工艺，是直接获取煤层及间接获取煤层气地质特性的一种有效手段，已被广泛应用于煤储层评价、钻井地质导向、固井质量评价等环节[6-8]。

近年来,研究者利用测井资料与实验室煤岩样品含气量数据，推演出不同的煤储层含气量预测模型。所用的方法主要有一元线性回归、多元线性回归、复合参数模型、BP神经网络法、深度信念网格等[9-15]。因煤层性质、储层条件不同，测井响应值不同，各预测模型具有地质针对性和地域特点。15#煤是寿阳区块煤层气开发的主力煤层之一，埋深在1 000 m以深的地区占85%以上，煤层埋深大，现有绳索取心存在煤心暴露时间长，保压困难，损失逸散气量高问题，造成含气量测试值不准确；同时，变质程度高，气含量测试存在时间长、时效慢等问题。如何利用测井数据，构建准确含气量估算模型，及时快速了解研究区深部气含量，是研究区CBM勘探开发的一个主要问题。

以沁水盆地寿阳区块为例，开展煤层含气量与测井参数的相关性分析，综合考虑各测井参数对含气量影响，建立基于测井响应的煤层含气量复合参数预测模型、多元线性回归预测模型和BP人工神经网络预测模型，并对三种含气量预测结果的适用条件和准确性进行了对比。

1 概况

图1 15#煤顶面构造图Figure 1 Coal No.15 top surface structures

2 含气量与测井参数相关性分析

地质构造、煤层顶底板、有效埋深、煤岩煤质和煤变质程度等是影响煤层含气量的主要地质因素，这些因素也决定了煤层气测井响应值[16]。与常规储层相比，煤储层具有“三高二低”测井响应特征。

选择研究区内煤层气井分布均匀且测井资料齐全，同时已经进行含气量测试分析的30口井73个样品(图1)，在岩心归位基础上，读取岩心测井层段平均值作为测井响应值，开展了煤岩样品空气干燥基含气量与之对应煤岩样品的埋深、补偿密度、自然伽马、补偿中子、声波时差、深侧向电阻率的相关性分析(图2)。

1)埋深与含气量相关性分析，随埋深增加，一方面上覆地层压力增大，煤吸附气体能力增强，另一方面煤层气的保存能力增强，含气量随之增加[17]。研究区含气量与埋深呈对数函数关系(图2a)，相关性较高。

2)补偿密度与含气量相关性分析，煤是一种碳氢高分子化合物，决定了煤体具有较低的密度，吸附气体后，煤体密度进一步减小，因此，气含量与补偿密度呈现负相关关系(图2b)。

3)自然伽马与含气量相关性分析，自然伽马对煤层矿物质敏感，煤岩中主要放射性沉积物吸附在黏土物质上，黏土矿物含量越高，自然伽马越高，气含量越小，因此，含气量与自然伽马呈现负相关关系(图2c)。

4)补偿中子与含气量相关性分析，补偿中子测井反映煤层孔隙度，影响煤的吸附性，孔隙度越大，越有利于煤层气吸附，煤层含气量越高，因此，含气量与补偿中子呈正相关关系(图2d)。

5)声波与含气量相关性分析，声波在煤层中传播速度低，声波时差表现为高时差。声波时差对含气性敏感，煤储层含气性增高，声波传播速度减少，声波时差增大，因此，含气量与声波时差呈现正相关性(图2e)。

6)电阻率与含气量相关性分析，煤和其他岩石一样，是一种导体，其电阻率受煤岩成分、煤变质程度、矿物质含量及层位地层水及孔隙度等因素影响[18]，研究区煤层深侧向电阻率主要分布在10～10 000 Ω·m，数值变化大，说明煤储层结构、物性等变化复杂，含气量与深侧向电阻率关系不明显(图2f)。

图2 测井参数与煤层含气量交会图Figure 2 Cross plot of logging parameters and coal gas content

3 含气量解释模型

由于煤储层结构复杂，导致测井响应与煤层地质条件之间的对应关系复杂，无法靠单一的测井资料对煤层含气量进行准确解释[19]。因此，有必要利用多参数建立含气量解释模型。

按照测井参数与含气量拟合的相关系数大小对各测井曲线进行排序，依次为埋藏深度、补偿密度、自然伽马、补偿中子、声波时差、深侧向电阻率。考虑到深侧向电阻率与含气量的相关性较弱，选择煤层埋深、声波时差、补偿中子、补偿密度和自然伽马构建煤层含气量解释模型。

3.1 复合参数解释模型

煤层深度、声波时差、补偿中子与含气量为正相关关系，补偿密度和自然伽马与含气量为负相关关系，采用五个测井响应参数构建复合参数Cp，建立其与含气量的关系模型如下：

(1)

GC=f(lnCp)

(2)

式中：AC为声波时差，μs/m；GR为自然伽马，API；DEN为补偿密度，kg/m3；CNL为补偿中子，v/v，Cp为复合参数，Gc为含气量，m3/t。

采用线性拟合方法得到寿阳区块含气量复合参数解释模型：

GC=5.527 2×lnCp+7.970 5

(3)

复合参数模型解释含气量与实测含气量对比如图3所示。

图3 复合参数解释含气量与实测含气量对比Figure 3 Comparison of composite parameters model interpretedgas content and measured gas content

3.2 多元线性回归解释模型

采用多元线性回归方法，建立煤层深度、声波时差、补偿中子、自然伽马和补偿密度5个因素与含气量的关系，得到含气量解释模型：

Gc=7.838 8+0.003 8×DEPTH+0.033×AC

+20.702 7×CNL-0.070 5×GR

-0.012 7×DEN

(4)

模型相关性系数R2=0.717 5，F=34.039 3，p=3.857 7e-17。线性回归显著性水平a=0.05,多元回归的样本容量M=73,回归方程n=5,查表得到F0.05(n,M-n-1)=F0.05(5,67)=2.352<34.039 3,且与F对应的概率p<0.000 1。因此，含气量与5个参数多元线性关系显著，多元回归关系成立。

多元线性回归模型解释含气量与实测含气量对比如图4所示。

图4 多元线性回归解释含气量与实测含气量对比Figure 4 Comparison of multivariate linear regression model interpreted gas content and measured gas content

3.3 BP神经网络预测模型

BP神经网络通过已知样本数据训练模型得到映射关系，其实质是求误差函数的最小值，通过调整网络权值和阈值，使误差函数下降，达到网络预测值逼近期望值的目的。BP神经网络具有较强的非线性逼近能力，应用广泛。对于含气量的预测，BP神经网络模型如图5所示。拟合变量5个，即输入层节点5个，输出层节点1个，即含气量值。

图5 含气量BP神经网络预测模型拓扑图Figure 5 Topography of gas content BP neural network prediction model

借助编程，进行BP神经网络预测模型的构建，训练100个神经网络模型并对预测含气量结果求平均值。对于隐含层数量，根据经验公式可在4～12之间选取，在单个神经网络训练规程中，对隐含层数量进行敏感性分析，选择均方误差最小时所对应的隐含层数量进行神经网络的构建。最终得到神经网络解释结果与实测含气量结果如图6所示，结果表明，神经网络模型解释精度高，解释值与实测值相对误差小。

图6 BP神经网络解释含气量与实测含气量对比Figure 6 Comparison of BP neural network model interpreted gas content and measured gas content

3.4 不同模型对比分析

分析73个样品的复合参数模型、多元线性回归模型和BP神经网络模型解释含气量的相对误差(图7)。整体而言，相对误差随含气量的增大而降低，整个样本平均相对误差分别为：复合参数模型16.84%，多元线性回归17.09%，BP神经网络模型11.33%，BP神经网络模型相对误差最低，精度更高。

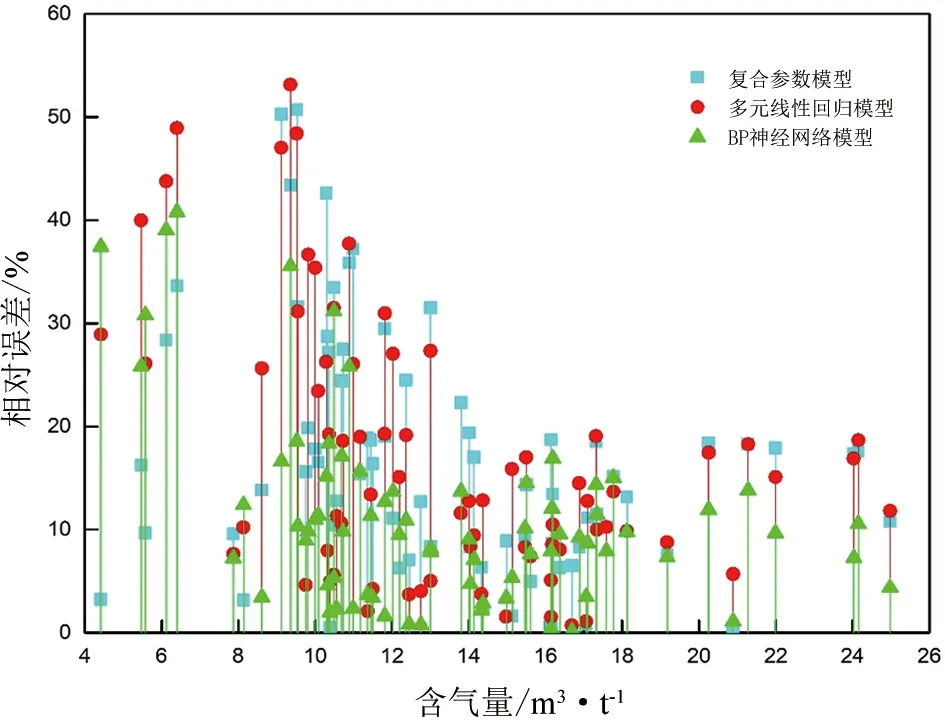
图7 三种解释模型含气量相对误差Figure 7 Relative errors of gas content interpretedfrom three interpretation models

为探究各个解释模型适应性，对比了不同含气量区间内的平均相对误差(图8)。由图可知，整体上多元线性回归和复合参数解释含气量相对误差呈先减小后增大趋势，BP神经网络模型相对误差则随着含气量增大逐渐降低。对于三种解释模型，含气量为12～20 m3/t，平均相对误差差别均较小，其他区间内三个解释模型差别明显增大。

图8 三种解释模型不同含气量区间平均相对误差Figure 8 Average relative errors of different ranges gas content from three interpretation models

当含气量小于8 m3/t时，复合参数模型解释含气量平均误差小于10%，这是因为构建复合参数模型后对其取对数，模型对低值更加敏感。当气含量大于8 m3/t时，BP神经网络模型预测含气量误差小于10%，解释精度更高。

进一步对比了不同深度区间内不同模型解释含气量的相对误差，结果如图9所示。当深度小于600 m时，复合参数解释模型相对误差较其他两种模型低。对于其他深度区间，BP神经网络模型平均误差小于15%，低于其他两种模型。

图9 三种解释模型不同埋深含气量平均相对误差Figure 9 Average relative errors of different coal buried depths gas content from three interpretation models

为准确解释寿阳区块15#煤层含气量，对于埋深在600 m以浅的煤层，优先选择复合参数模型和BP神经网络模型，600 m时以深的煤层则优先选择BP神经网络模型。

4 模型应用

应用构建的含气量解释模型，利用寿阳区块内2口不同埋深煤层气取心井进行含气量解释(图10、图11)。

图10 S-7井含气量解释成果Figure 10 Well S-7 coal gas content interpreted results

图11 S-11井含气量解释成果Figure 11 Well S-11 coal gas content interpreted results

成果图显示，煤层测井曲线响应表现为高补偿中子、高电阻率、高声波时差、低密度、低自然伽马，与顶底板岩性测井资料响应特征差别明显，第七、八、九道分别为利用复合参数模型、多元回归模型和BP神经网络模型解释含气量与实测含气量比对图。图中不同模型解释含气量误差不尽相同。

表1为2口井三种模型解释含气量和对应的相对误差。S-7井煤层埋深在495 m左右，平均含气量10.74 m3/t，复合参数含气量解释模型平均误差小于多元线性回归模型和BP神经网络模型；S-11井煤层埋深在1 415 m左右，平均含气量17.23 m3/t，BP神经网络含气量解释模型平均误差小于复合参数模型和多元线性回归模型。

表1 2口井含气量解释成果和相对误差情况

埋深浅的井，复合参数模型的解释精度高于其他两种模型，埋深深的井，含气量测试值较高，三种解释模型误差均在15%以下，含气量解释误差基本可以满足勘探要求，但较其他两种解释模型，BP神经网络模型的解释精度更高，与模型适用性分析结果一致，后期可推广到整个寿阳区块。

5 结论

1)应用煤层含气量与测井参数相关性高的煤层埋深、补偿密度、自然伽马、补偿中子、声波时差五个参数，分别采用复合参数法、多元线性回归法和BP神经网络法构建了寿阳区块15#煤层含气量解释模型。

2)各模型适用性和准确性对比结果表明：BP神经网络解释含气量模型平均相对误差低于复合参数模型和多元线性回归模型；复合参数模型对600 m以浅和含气量低值解释精度高；BP神经网络解释模型对600 m以深煤层和含气量高值解释精度高。

3)基于测井参数构建的复合参数模型和BP神经网络模型，在煤层气井含气量预测中，预测值与实测值具有较高的吻合度。可作为寿阳区块煤层含气量预测的一种新方法。