复合极值分布在台风风暴潮增水重现期计算中的应用研究
付翔,梁森栋,李涛,吴少华
(国家海洋环境预报中心,北京 100081)
1 引言
风暴潮灾害是我国最主要的海洋灾害,特别是台风风暴潮。自1989年有统计数据以来,风暴潮(含近岸浪)灾害造成的直接经济损失占全部海洋灾害直接经济损失的90%以上,严重的台风风暴潮灾害几乎每年都会在不同地区发生[1]。因此,在涉及海洋工程建设、海岸环境损害评价、保险的灾害风险计算以及气候变化影响评估时,需考虑风暴潮的致灾危险性。风暴潮致灾因子的危险性体现在风暴潮的强度、频率以及叠加浪、涌和天文潮后引起的高潮位上,极值发生频率(P)是常用的定量化指标之一[2-3]。
极值发生频率和重现期(T= 1/P)传递的是极端事件最大可能的信息。它有两层含义:一是对于某频率p的极值,下次出现该值的平均等待时间为Ta;二是在Ta 里出现该极值的次数平均是1 次[4]。对于台风风暴潮,由于台风影响具有随机性,某一区域并不是每年都遭受显著的台风风暴潮,但在某些年却可能遭受一次以上的台风风暴潮灾害,例如2014 年连续遭受台风“威马逊”和台风“海鸥”袭击的雷州半岛,以及2015 年台风“苏迪罗”和台风“杜鹃”连续登陆的福建中部。因此,如果使用年极值法来计算风暴潮重现期,每年只取一个极值,有可能会取到无台风或弱台风影响年的小值而舍去了频发年的次大值,使得计算数据失真,估算的重现期极值出现较大偏差。考虑随机事件发生次数的复合极值分布可以有效地解决这一问题。
引入一个描述无规律事件发生次数的离散型概率分布——Poisson 分布,使其与一个连续型的极值分布复合,组成的复合极值分布不仅能拟合每年实测变量随机的数据序列,对于资料年限较短的情况也能可靠应用[5]。复合极值分布提出后,不少学者在台风波高、极值风速和风暴潮的计算预测中进行了研究和应用[6-10]。目前Poisson-Gumbel 复合极值分布已被推荐用于台风波高的设计值计算[11-12]。本文将该分布法用于台风风暴潮的重现期计算,分析其优缺点及应用效果。
2 计算方法和资料
2.1 极值Ⅰ型频率曲线分布
港口与海岸工程设计中,常采用极值Ⅰ型分布律推求指定频率或重现期的风暴潮和极端高低潮位值[11-12]。它是广义极值分布(Fisher-Tippett)的一种,最早由Gumbel[13]用于水文统计。其概率分布函数为双指数形式,表示为:

式中,μ为位置参数,即分布的众数;α为尺度参数,代表分布的离散性。这两个参数可用多种方法进行估计[14-15]。
2.2 离散型Poisson分布
连续的极值Ⅰ型分布律仅能用于规律的极值样本,如年极值或月极值等。而对于某一地区,每年台风风暴潮的发生次数和强度都是随机的,它们构成的是离散型分布。描述稀有事件发生次数的Poisson 分布非常适合用以描述台风风暴潮的发生概率。假定某地一定强度以上的台风风暴潮的发生频次n符合Poisson分布,其概率质量函数表示为:

式中,λ为年平均台风风暴潮发生次数。
2.3 Poisson-Gumbel复合极值分布
根据复合极值分布式[5-6],给定设计频率p′的极值分布为:

式中,p= 1 -p′。定义称为重现期。将式(1)、(2)代入(3),则某T年一遇的台风风暴潮值xp可表示为:

具体推算见文献[6]。
2.4 过阈法
过阈法(Peak Over Threshold,POT)是极值理论下确定计算样本序列的一种方法,即先确定某一观测值下限(阈值),凡超过此值的均列入统计序列,而后再进行极值分布拟合。阈值的确定十分关键,阈值过高会使可利用的样本数过少,从而导致分布函数估计的参数方差偏高;阈值过低又会使分布的渐进性得不到满足,产生有偏估计。阈值的选取有多种方法,如平均剩余寿命图法(Mean Residual Life Plot)、平均超越期望图法(Mean Excess Plot)、Hill 图(Hill plot)等。计算法包括峰度法和渐进均方误差法等。
2.5 资料来源
台风信息采用中国气象局的《台风年鉴》(1980—1988 年)和《热带气旋年鉴》(1989—2016 年),以及热带气旋资料中心最佳路径数据集[16](网址:http://tcdata.typhoon.org.cn)中的资料(2017—2019年)。风暴潮数据来自国家海洋环境预报中心,在“908”专项台风风暴潮灾害历史数据集基础上进行延长和补充,增水值由台风影响期间测站实测逐时水位值去除天文潮得到,实测水位值根据国家标准[17]进行观测,数据经过严格的质量控制,排除了由于台站迁址、仪器变更和地面沉降等产生的影响。
3 计算个例
三沙验潮站位于福建省东北部(见图1),几乎每年都会受到台风影响。以其为例,利用Poisson-Gumbel复合极值分布计算其多年一遇台风风暴潮。
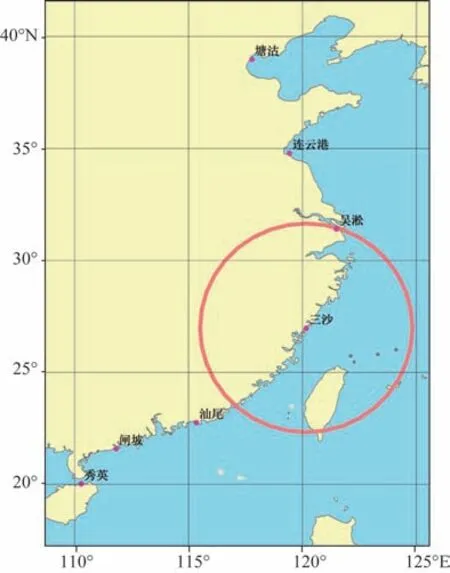
图1 部分代表验潮站分布图Fig.1 Location of some typical water gauge
第一步:确定阈值。采用平均剩余寿命图法[17]和百分位法确定阈值范围,挑选1980—2019 年间进入距三沙站约500 km 范围以内的台风,共计171个,统计每次过程的最大风暴潮值,剔除其中的减水过程后建立经验频率序列。根据平均剩余寿命图(见图2),考虑到近似线性和置信区间范围[18],阈值可在20~80 cm 之间选取。取其中值,同时也是增水极值累积频率的中位数50 cm 为统计阈值(见图3),使其发生次数符合Poisson分布。

图2 三沙站台风风暴潮增水极值序列平均剩余寿命图(虚线为95%置信区间)Fig.2 Mean residual life of typhoon storm surge extreme value in Sansha station(The dotted line is the 95%confidence interval)

图3 三沙站台风风暴潮增水极值累计频率曲线Fig.3 Accumulative frequency curve of typhoon storm surge extreme value in Sansha station
第二步:Poisson 分布检验。统计三沙站超过阈值的台风风暴潮过程,由式(2)计算其发生次数的理论频率分布(见图4),采用卡方分布χ2=进行检验。取显著水平0.05,查自由度为5(k- 1)的卡方分布临界表= 11.07,由χ2<χ02.05可知三沙站最大增水50 cm以上的台风风暴潮发生频数符合Poisson分布。
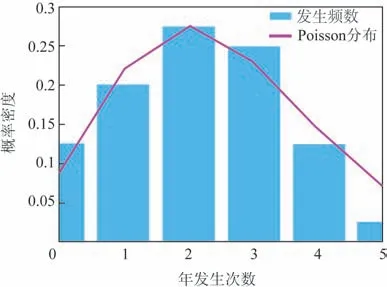
图4 三沙站台风风暴潮发生频次及概率密度分布Fig.4 Distribution of probability density and typhoon storm surge occurrence frequencies in Sansha station
如果发生频数拟合不能通过检验,则应该适当提高阈值大小减少样本量,再进行表1计算,直至通过检验。

表1 台风风暴潮发生次数拟合检验Tab.1 Fitting test of the number of typhoon storm surge events
第三步:Gumbel 分布检验。P-P 图是变量的累计比例与指定分布的累积比例之间的关系图,可直观地检验样本数据是否符合指定概率分布。当数据符合指定分布时,P-P图中各点近似呈一条直线,即代表样本数据的点基本在代表理论分布的对角线上。根据P-P 图,三沙站过阈台风风暴潮极值序列符合Gumbel 分布(见图5),也可采用Kolmogorov-Smirnov 检验进行数据序列的Gumbel分布检验。

图5 Gumbel分布概率检验图Fig.5 Gumbel distribution probability plot
第四步:复合极值分布拟合。根据式(4)拟合三沙站过阈风暴潮增水极值序列,利用有限样本分布函数代替总体分布函数的Gumbel 法[13]估算参数μ和α,然后计算不同重现期的台风风暴潮极端增水值。
4 比较分析
4.1 与年极值序列计算结果比较
建立三沙站1980—2019 年的台风风暴潮年极值增水序列,利用Gumbel 分布拟合计算三沙站台风风暴潮多年一遇重现期增水值,与复合极值分布拟合的结果进行比较(见表2)。结果显示,对于10年一遇以下增水,Gumbel计算的增水值比复合分布拟合的结果小,而对于10 年一遇以上增水,Gumbel计算值比复合分布拟合的结果大,且随着重现期增大,差比也增大。在中高频次发生范围内,两种分布的计算值比较接近,但在高频次和低频次发生范围内的计算差异较大。究其原因,采用年极值序列拟合计算时,由于无台风影响年低值的存在会导致Gumbel 曲线的斜率增大,使得高频发生值更小,低频发生值更大;而过阈法序列不仅包含了在相同年份发生的高值,还剔除了弱过程,避免了增水小值带来的较大观测误差和潮汐预报误差,但由于相对低值样本增多,导致低频次发生的风暴潮值计算偏小。

表2 不同分布拟合的重现期增水值比较(单位:cm)Tab.2 Comparison of surge return values between different distribution(unit:cm)
根据三沙站台风风暴潮原始统计序列,40 a 间增水大于79 cm 的过程为33 次,约为1.2 年一遇;增水大于90 cm 以上的过程为23 次,约为1.7 年一遇;增水大于95 cm 的过程为20 次,正为2 年一遇。可见Poisson-Gumbel复合极值分布的高频次发生值的结果更为合理。另外,由图6也可看出,对于过阈原始序列的拟合,复合极值分布对极大值的拟合结果明显好于Gumbel分布。
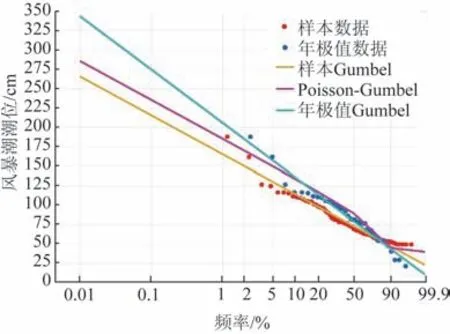
图6 分布拟合比较Fig.6 Comparison between curves of different distribution
4.2 阈值敏感性试验
由于接近阈值的小值数量的多少对拟合估算结果影响较大,因此需要调整阈值大小,比较不同阈值下样本序列的复合分布拟合结果。取最大增水阈值60 cm、65 cm、70 cm 和最高75 cm,分别截取台风风暴潮过程样本序列进行复合分布计算。所有序列的发生频数分布均通过0.05 显著性检验的Poisson 分布。结果显示(见表3),阈值选取增加,所有重现期的计算值都会升高,在阈值为70 cm时达到最高值,后又开始下降。文献资料显示[19],三沙站1949 年以来台风风暴潮极值为190~200 cm(6614 号台风风暴潮),与阈值为70 cm 和75 cm 的计算结果相近。由此可见,虽然高频次发生值的估计偏高,但对于低频范围的高年遇值,高阈值序列的拟合效果更好。

表3 拟合不同阈值样本的Possion-Gumbel复合分布重现期增水值比较(单位:cm)Tab.3 Comparison of surge return values of Poisson-Gumbel distributions fitting samples with different threshold(unit:cm)
4.3 分段计算结果比较
根据相关标准[11-12],在进行极端水位值确定时,应用不少于连续20 a的潮位实测资料进行计算。将三沙站40 a 的资料序列分为前20 a 和后20 a,以阈值70 cm 为例(其余结果略),分别对两种方法的拟合计算进行比较,结果见表4。我们发现,两种方法两个时间段的差值均自高频向低频增大,复合分布结果仅在高频处差值较小,10 年一遇以上低频结果两个时间段的差值的复合分布远高于Gumbel 年极值分布。其原因在于三沙站这两个时间段的台风风暴潮极值序列差别较大,前20 a 极值偏小且分布均匀,以阈值70 cm 为例,前20 a 的极值样本仅为18个,均值为89.8 cm,标准差为16.8 cm;而后20 a的样本为26 个,极值均值为99.7 cm,标准差为27.3 cm。样本数据的较大差异导致了复合极值分布对低频发生值的估算差别显著,前20 a 数据的计算值严重偏低。
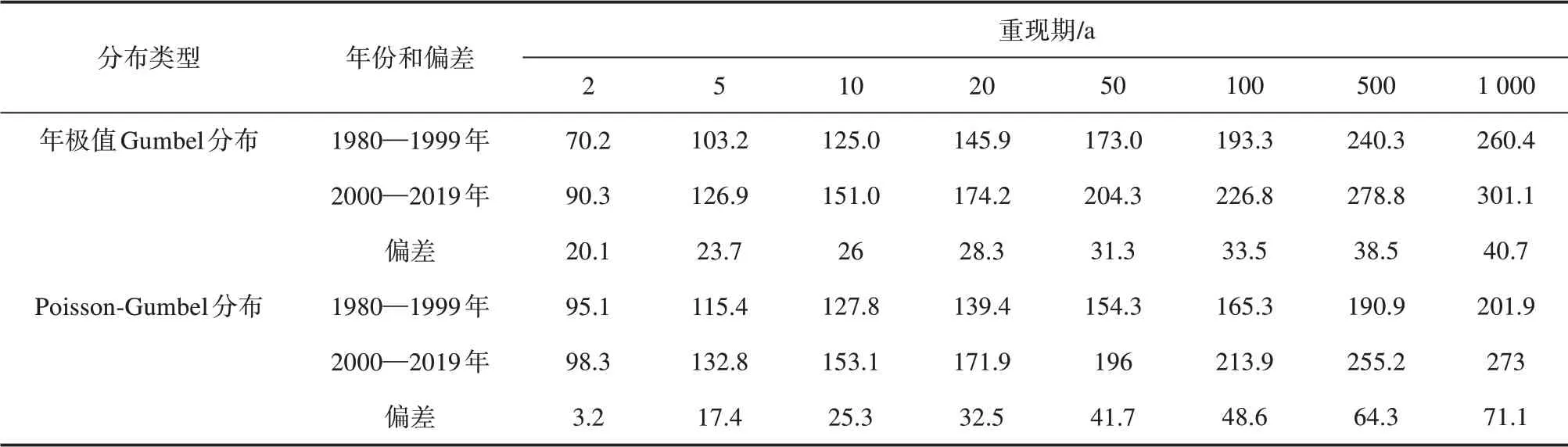
表4 连续分段20 a样本数据重现期增水值比较(单位:cm)Tab.4 Comparison of surge return values between different distribution of consecutive 20 a subsection data(unit:cm)
在包含有40 a间最大增水的原始过阈样本和年极值样本中,任意挑选两组20 a 的数据序列进行两种分布拟合计算,由于观测年代较短,复合分布应取低阈值以增加样本数量,这里取50 cm。由两种分布的两组结果比较可见(见表5),在观测年代较短且样本较少的情况下,复合分布的拟合结果比单一的年极值Gumbel 分布结果更为稳定,两组数据结果的差值更小,低频值也更为合理。

表5 随机分段20 a样本数据重现期增水值比较(单位:cm)Tab.5 Comparison of surge return values between different distribution of random 20 a subsection data(unit:cm)
5 沿海代表站台风风暴潮重现期分布
根据第2 部分的计算步骤,选取部分代表验潮站(见图1),利用Poisson-Gumbel 复合分布拟合1980—2019 年40 a 的台风风暴潮增水极值序列,计算出各站50 年一遇和100 年一遇的台风风暴潮增水值,阈值选取均在累积分布中位数附近并保证序列通过分布检验。由表6 可见,塘沽、吴淞、闸坡和秀英站可能遭受的台风风暴潮强度较强,不仅增水值大,100年一遇和50年一遇增水的差值也大,发生频次低的风暴潮强度更强,说明台风在这些地方可能引起的极端风暴潮更高,危险性也更大。

表6 各站台风风暴潮重现期值(单位:cm)Tab.6 Return values of typhoon storm surge in several typical stations(unit:cm)
6 小结
考虑随机事件发生频率的Poisson-Gumbel复合极值分布是解决观测资料年限较短或是出现无年极值(无台风影响)情况下,风暴潮极值重现期计算的有效方法。复合极值分布的计算结果对样本数据较为敏感,特别是标准偏差较小的样本数据,低频次发生值的计算结果显著偏低。阈值的选取对结果影响较大,对于较长时间序列数据,复合分布的阈值取值偏低则高频次发生值更准,阈值取值偏高则低频次发生值更准;而对于短时间序列数据,复合分布的计算结果更稳定,且对低频发生值的估算也更准,此时由于样本数量较少,应取偏小阈值以增加样本数量。对几个典型潮位站的重现期计算表明,塘沽、吴淞、闸坡和秀英站台风引起的可能极端风暴潮较强,台风风暴潮致灾危险性较高。
复合分布在风暴潮极值计算中的特征可延伸至潮位极值计算。但由于其对数据样本的敏感性,在工程应用中,仍建议以差比法延长资料年限后再行计算。若考虑无年极值或一年多极值的情况,则需根据对高频值或低频值的需求,确定具体阈值。

