Effects of Binaries on Open Cluster Age Determination in Bayesian Inference
Zhong-Mu Li,Su Zhang,Jing Chen,Wen-Chang Zhao,and Wu You
Institute for Astronomy,Dali University,Dali 671003,China; chenjing05@tsinghua.org.cn
Abstract We investigate the effects of binaries on the cluster age determination for 561 open clusters in the Galactic disk via the Bayesian statistical framework.Stellar properties of these star clusters,including age,metallicity,distance modulus,color excess,binary fraction,and rotating star fraction,are derived from color–magnitude-diagrams(CMDs)via isochrone fitting to high-precision Gaia EDR3 data.Across the simple stellar population of binary and single-star,age differences can be found with the same star cluster.A Bayesian applied regression modeling software,Stan,is employed to explore how much binaries affect the age determination of open clusters.Our results present less statistically significant difference between the binary-star simple populations(bsSSPs)and the singlestar simple populations (ssSSPs) for cluster age determination.For all clusters in our sample,the ages estimated using the bsSSPs models are younger than those estimated using the ssSSPs,with a mean value of ∼70 Myr.However,it is found that for 52.5%clusters in our sample,ages are relatively sensitive to the presence of binaries,at least ∼25% younger.This suggests that in studies of open cluster age determinations,the effects of binary interactions on the whole sample are not prominent,but its effects on some clusters should still be included as an essential ingredient.
Key words: (stars:) Hertzsprung-Russell and CM diagrams–(Galaxy:) open clusters and associations–methods:statistical
1.Introduction
Open clusters are crucial for tracing the formation and evolution histories of our galaxy.The basic parameters of stars clusters,i.e.,age,metallicity,distance modulus,and color excess can be obtained by fitting the color–magnitude diagrams(CMDs).Building the stellar population is an efficient approach to infer the parameters of clusters via isochrone fitting.Accordingly,there are many publicly available stellar evolution codes such as PARSEC(Bressan et al.1993),Y2(Yi et al.2001),DSED(Dotter et al.2008),GENEC(Ekström et al.2012),MIST (Choi et al.2016),and more.For example,Choi et al.(2018) used Gaia Data Release 2 (DR2) to investigate stellar parameters of three open clusters,NGC6819,M67 and NGC6791.Bonatto (2019) obtained astrophysical parameters of star clusters using CMD fitting;Gontcharov et al.(2020)studied some parameters of the Galactic globular cluster NGC6205 (M13) in detail using five theoretical models and isochrones to fit the observed CMD;Piatti (2021)made use of CMDs of 17 age gap star clusters to confirm their ages.
The impact of rotation and age spread on the CMD morphology of clusters can affect the ages determined.Especially,clusters younger than about 2 Gyr exhibit split main sequences and extended main-sequence turn-offs (eMSTOs) in Magellan Clouds and Galaxy (e.g.,Mackey &Broby Nielsen2007;Cordoni et al.2018;Marino et al.2018a;Milone et al.2018).D’Antona et al.(2015) and Georgy et al.(2019)conclude that rotation can affect the colors and magnitudes of stars in clusters from the stellar evolution theoretical.Different rotation rates provided by spectroscopy reveal the eMSTOs of NGC1866,NGC1818 and M11 (Dupree et al.2017;Marino et al.2018a,2018b).Additionally,age spread can contribute to the eMSTOs (Milone et al.2017).In view of the above causes,we only choose the simple stellar population,and the rotating star fraction is identical in building the simple stellar population of binary and single-star for the same cluster.However,binaries are seldom considered in building stellar population models.It is well known that binary interactions are one of the causes for the extended main-sequence turnoffs,blue stragglers and split main sequences (e.g.,Li et al.2017b;Li &Mao2018;Cohen et al.2020;Chen et al.2022).Binaries take a significant fraction of cluster members.(e.g.,Sana et al.2009;Raghavan et al.2010;Milone et al.2012;Li&Mao2018;El-Badry et al.2021;Wang et al.2022),and they serve as laboratories for studying the supernovae(Mazzali et al.2018),hunting for gravitational wave signals (Nelemans2018;Smith et al.2021) and tracing the chemical evolution of galaxies (Tsujimoto et al.1995;Wang et al.2020b).Furthermore,the shape of CMD changes can impact the measurement of stellar properties.The effects of binaries are sensitive to assumed cluster parameters such as age.Instead,from their study of 60 globular clusters,Milone et al.(2012)and Milone et al.(2016)conclude that the binary fraction correlates with cluster mass and does not depend on the other cluster parameters such as age,HB morphology,ellipticity,metallicity,collisional parameter,and so on.However,their work is focused on old star clusters only.Here,we study open clusters that span a wide age range of 0.1–7.8 Gyr.It is viable to study the relation between the binary interactions and age determination of open clusters,e.g.,those in the Gaia Early Data Release 3 (EDR3) data.
Binary-star stellar population models for CMD analysis of star clusters have been presented in the past(e.g.,Li et al.2014;Belloni et al.2017;Li et al.2017a;Li &Deng2018;Luo &Li2018;Li et al.2020;Han et al.2020).Recently,from white dwarf-main sequence binaries,Rebassa-Mansergas et al.(2021)suggest that there is a relation of scatter of[Fe/H]with 0.5 dex between the age and metallicity.In conclusion,it is essential to take binaries into account when estimating the age of star clusters.
Bayesian techniques have been applied to infer cosmological parameters (e.g.,Jasche et al.2010;Li et al.2013;Sahlholdt et al.2019;Mandal et al.2021).Recently,Valcin et al.(2020)presented a Bayesian approach to fit the full CMD morphology and derived the absolute ages of 68 old globular clusters,then an age of the universe was educed.Following this work,Valcin et al.(2021) provided an uncertainty of 0.27 (0.36) Gyr of the age determination of star clusters based on the morphology of the RGB in the CMD of globular clusters degenerated with αMLT.It has been proved that the age of the universe inferred from ages of the old globular clusters agrees with that of the Λ CDM model.However,the two papers do not take effects of binaries into account and the reliable measurement of cluster age remains to be needed.
Li et al.(2021) studied the fundamental parameters of 49 new star clusters that were found by Liu &Pang (2019) via a powerful tool of CMD.However,there are some age differences for the same star clusters in different works,and the stellar model variability seems a plausible cause for explaining this case.Therefore,it means that the age determination of star clusters is due to metallicities,age spread,interacting binaries and fast rotating stars.At present,some literatures focus on metallicities,age spread,fast rotating,the amplitude of photometric variability and so on,which can affect the age determination of star clusters.Some comments can be found in the papers (e.g.,Gossage et al.2018;Catelan2018;Wang et al.2020a;Anders et al.2021;de Freitas2021).Li &Han (2008) investigated the effects of binary interactions on age and metallicity of star clusters based on the isochrone and spectral energy distribution fittings,but its results were mainly obtained from the theoretical side on account of the limitation of computing ability.Chen et al.(2021) found that the age of clusters obtained from the singlestar simple populations (ssSSPs) was larger than one from the binary-star simple populations (bsSSPs) with a mean of 1.2 Gyr,but a major limitation is that the sample size of 46 star clusters was not enough large.In the following,due to the main parameters of star clusters acquired from LISC catalog,it is important to further explore this problem and considerably enlarge the sample to quantify the impact of binaries on age determination of star clusters.Simultaneously,it is useful to estimate a more accurate age of the cluster and can provide a better reference for revising an age uncertainty with open clusters.
Before evaluating how much binaries have influenced the cluster age determination,it is important to have reliable estimates of the stellar population properties.Using the advanced stellar population synthesis (ASPS) model (Li et al.2016),we build the simple stellar populations of binaries and single-stars,and the fundamental parameters of star clusters can be obtained by the best-fitting populations via the CMD fitting tool Powerful CMD(Li et al.2017a).In this work,based on the observational investigations,we select 561 open clusters from LISC catalog to study this case in the Bayesian statistical framework,in which the clusters spread a large age distribution from 0.1 to 7.8 Gyr.The age differences between the bsSSPs and ssSSPs models can be detected.Then we fit the Bayesian linear regression models to predict the effects of binaries on the cluster age determination.In Section2we present the sample selection process,and in Section3we explain the methodology of Bayesian technique.Results are presented in Section4,followed by the summary and discussion in Section5.
2.Star Cluster Sample
The star cluster sample used by us comes from the Milky Way.Accompanying the Gaia EDR3 release,we have completed the data processing,from downloading data,deriving a clean sample of member stars,identifying star clusters,isochrone fitting,obtaining the best-fitting stellar population to deriving the reliable parameters (age,age spread,metallicity,distance modulus and color excess,binary fraction and rotating star fraction).Based on the above framework,A LISC catalog of star clusters I (Li et al.2022) has identified 3 597 star clusters and main parameters of 655 clusters have been acquired reliably.From the LISC catalog of star clusters,we collect the simple stellar populations of binaries into a star cluster sample,and it is comprised of 561 open clusters,covering ages from 0.1 to 7.8 Gyr and the binary fractions from 0.11 to 0.55.The ages and binary fractions of 95%clusters are concentrated in 1–2 Gyr and∼0.5,respectively.In our sample,each CMD has a clear main sequence and turn-off,and the photometry of these star clusters has been corrected for differential reddening as the work of Milone et al.(2012).Figure1displays the procedure to correct photometry for the differential reddening.

Figure 1.Procedure to correct photometry for the differential reddening of stars in the CMD.(a)Original CMD is rotated about 70◦counterclockwise near the mainsequence turn-off,as the red arrow direction.(b)Fiducial line(dashed red line)is fitted by a cubic spline,using median points for main sequence stars in each 0.2 mag bin of ordinate.(c)Reddening variation of a star (continuous red line) is estimated by the median of target stars (red points)with respect to the red fiducial line.(d)Corrected CMD is obtained by calculating the differential reddening suffered by each star through this procedure run about four iterations.
The stellar population properties,i.e.,age,distance,metallicity,color excess,and binary fraction have been already determined reliably by comparing isochrones from bsSSPs with the observed CMD.For this work,it is critical to credibly define the age of the same cluster via ssSSPs models.In order to ensure the best quality of our data,we not only use the weight average difference (WAD) (Li et al.2015) as a goodness indicator,but also manually check the best-fitting CMDs for each investigated cluster.Figure2shows a comparison of ages obtained by the two stellar populations.In order to obtain a robust value on cluster age determination,the best-fitting CMD takes the full morphology of the CMD into account including the red clump giant.In this case,the synthetic CMDs of the cluster LISC0109,0189 and 0309 in Figure2for ssSSPs display the poor fits.We note that an uncertainty for the stellar population model is ∼0.1 Gyr,as shown in Figure3.

Figure 2.CMDs of eight star clusters for comparison of effects of binaries on the cluster age determination.Blue crosses and color points denote the observed and best-fitting CMDs,respectively.

Figure 3.Similar to Figure 1 but for LISC2695.

Figure 4.Top: Checking graphical posterior predictive in the single-level (left side) and in the two-level models (right side).Thick lines show observed data distributions derived from 300 simulated data sets from the posterior predictive distribution(thin lines).Bottom:The trace plots for the regression coefficient(slope)of the tbsp variable.The four chains are all convergent from noise.
3.Methodology
In this section we provide some details on how much the binaries have influenced the cluster age determination by means of the Bayesian statistical framework.
In this work,we divide the age data of our sample into two subsamples with different ages of the same cluster.One is derived from the bsSSPs (tbsp) and the other is derived from ssSSPs (tssp),which differ in whether binary is taken into account but other star cluster parameters are identical.First we adopt a Markov Chain Monte Carlo(MCMC)sampling method to calculate marginalized probabilities of age data,and then we fit the Bayesian linear models to predict thetbspfromtssp.Finally,the reliable estimates of quantities can be obtained in Bayesian statistic framework.
We briefly review the fundamentals of modeling the Bayesian statistical framework (Muth et al.2018).The logarithm of the Bayesian theorem is defined as:
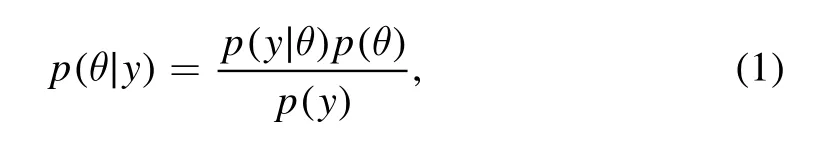
wherep(θ|y),p(y|θ) andp(θ) are the posterior probability distribution,prior distribution and likelihood function of parameters θ given datay,respectively.p(y) is the marginal distribution,and it is used as the normalizing constant,so for regression models Equation (1) included the regressors can be exchanged by

wherexis the predictors for regression models.
The following is the basic mathematical formulation of linear regression model.The single-level regression model is specified as
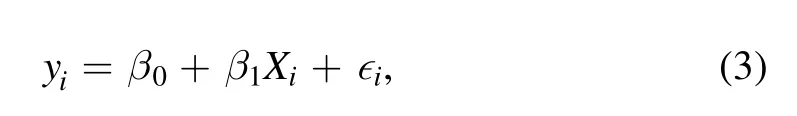
where ∊iare the errors,that is ∊i∼Normal(0,σ2).The model also be expressed as

where σ2corresponds to the variability with which the outcomes deviate from their predictions based on the model.yiis the outcome for theith observation.Xiis theith predictors.The parameters β0and β are the intercept and vector of regression coefficients,respectively.
As before,the two-level regression model can be written as
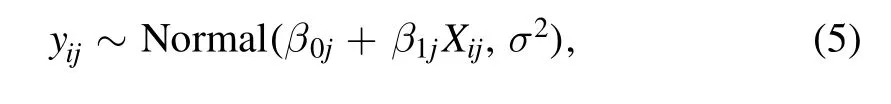
whereyijis the outcome for measurei=1,…,Ijforj=1,…,J,with individualjhavingIjtotal observations.A two-level linear model is an extension of single-level linear regression,in which the individual parameters are assigned a joint distribution with all parameters.
For this work,we take advantage of an experienced Bayesian software,Stan·rstanarm (Ben et al.2020),to fit the Bayesian single-level and two-level regression models.The plots in Figure4show the parameter estimations of our sample applying Bayesian linear regression models from MCMC draws.The top panel of Figure4shows the graphical posterior predictive checks in the single-level (left)and two-level(right)linear regression models fortbspdata.The trace plots in the bottom panel of Figure4are for the slope of thetbspvariable.

Figure 5.Left:The 1D plots show the distributions of tbsp,tssp and residual.Each age of star clusters is shown as a colored point,where the color corresponds to the residuals between the values of tbsp and tssp shown in the color bar.Right:Fitting a Bayesian linear regression(red line)to predict the quantitative result for all the star clusters.The points are the age parameters for each star cluster.The color bar shows the age difference for the same cluster.
4.Results
In order to generally estimate that how much binaries have influenced on the age determination of star clusters,we first use an MCMC sample analysis software,GetDist(Lewis2019),for Bayesian inference to explore the posterior distribution for age parameters of samples.In Figure5,from the “triangle” plot of MCMC parameter samples,the 1D plots are constructed from age data of all investigated clusters using kernel density estimates.The color points correspond to the values of the samples classified by Gaussian mixture model.We can see that the residuals of ages calculated from the two models are in a range of 0.3 dex,and its fine bins not large enough to well sample smoothing scale.The 2D contour,which lies in the second row of the right panel of Figure5is tightly correlated,that is,the magnitude of binaries influence is very slight.The other 2D contours show containing different fractions of the total probability for joint distributions of residuals and ages,and we can see that binary interactions can make the star cluster age smaller.Table1shows the age differences fitted by the two stellar population models.

Table 1Age Comparison of the Two Stellar Populations for 561 Star Clusters Sample

Table 2Diagnostics of the Estimated Parameters from the Single-Level Model Using Stan for 561 Open Clusters Sample
Second,we utilize Stan (Muth et al.2018),which is a software of the frontiers of applied statistics to fit Bayesian linear regression models.Table2shows the estimates for the intercept (β0) and the slope (β1) are 0.98 and−0.07 in our sample,respectively.This indicates that thetbspis similar totssp.
The plot in the right panel of Figure5illustrates the more accurate quantitative result using a Bayesian single-level linear model for all clusters.It is approximately written as

Considering an uncertainty for the system and observation is about 0.1 Gyr,although there are still some residuals with nonzero,the binary interactions have few effects on the open cluster age determination.
In Table1,the ages of 52.5% star clusters are variable between the binary-star stellar population and the single-star stellar population models.For these clusters (tbsp Figure 6.As the right of Figure 5,but for clusters with non-zero residuals. Table 3As Table 2,but for Clusters with Non-Zero Residuals in a Two-Level Linear Regression Model We have explored the effects of binaries on the cluster age determination via the Bayesian technique.The star cluster sample used in this analysis comprises of 561 open clusters with high-quality Gaia EDR3 data to derive the stellar ages via CMD fitting.Exploration of the results is that binary interactions cannot affect the age determination for 47.5%of our investigated clusters,while more than half of the clusters (52.5%),whose ages can be explained with younger by binary-star stellar population,at ∼150 Myr younger. Generally,compared to the traditional stellar population model analysis methods,the Bayesian applied regression modeling has a higher efficiency due to its ability to account for a large quantity of data and therefore gets better statistical properties.The results show that a prominent distinction between age distributions oftbspandtsspis not found among our sample.It is consistent with the finding of Milone et al.(2012),who suggests that there is a lack of statistically significant correlation between the binary fractions and parameters of star clusters. On the other hand,some clusters in our sample can be explained with younger binary-star isochrone,at least ∼25%younger.This agrees with the advisement of Mermilliod et al.(2001),Li &Han2008and Milone et al.(2009),which suggests that binary interactions,i.e.,mass transfer,collisions,supernova kicks,tidal interaction can make the color of the stars bluer and brighter,so the binary-star stellar population appears to have a younger age.Figure7shows a comparison of our result and the one from the other work of Li&Han(2008).As we can see,in particular,the two models are very similar in a range of 2.0–8.5 Gyr,which is exactly the stellar age scope of our sample.Our works not only can be tested with the stellar populations model on the theory side but also make meaningful comparisons between theoretical and observational investigations. Figure 7.Comparison of our result and the one from the other work of Li &Han (2008). In conclusion,the results can give us a flexibility suggestion that for the whole sample,binary interactions have a small effect on the parameters of open star clusters survey,but for some clusters,their effect should not be ignored. Acknowledgments This work is supported by the National Natural Science Foundation of China (No.11863002),Yunnan Academician Workstation of Wang Jingxiu (No.202005AF150025),Sino-German Cooperation Project (No.GZ 1284),and Research Fund Project of Yunnan Education Department (Nos.2020J0545 and 2021J0335). Data Availability The data underlying this article will be shared on reasonable request to the corresponding author.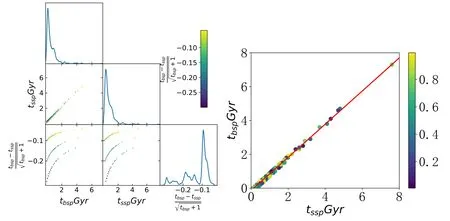

5.Summary and Discussion

 Research in Astronomy and Astrophysics2022年8期
Research in Astronomy and Astrophysics2022年8期
- Research in Astronomy and Astrophysics的其它文章
- A Baseline Correction Algorithm for FAST
- Ultra-wide Bandwidth Observations of 19 Pulsars with Parkes Telescope
- Correlation between Brightness Variability and Spectral Index Variability for Fermi Blazars
- HI Vertical Structure of Nearby Edge-on Galaxies from CHANG-ES
- Analyzing Dominant 13.5 and 27day Periods of Solar Terrestrial Interaction:A New Insight into Solar Cycle Activities
- Identifying Outliers in Astronomical Images with Unsupervised Machine Learning
