New Simulations of the X-Ray Spectra and Polarizations of Accretion-disk Corona Systems with Various Geometrical Configurations I.Model Description
Xiao-Lin YangJian-Cheng Wangand Chu-Yuan Yang
1 Yunnan Observatories,Chinese Academy of Sciences,396 Yangfangwang,Kunming 650216,China; yangxl@ynao.ac.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects,Chinese Academy of Sciences,Kunming 650216,China; jcwang@ynao.ac.cn
3 Center for Astronomical Mega-Science,Chinese Academy of Sciences,Beijing 100101,China
4 University of Chinese Academy of Sciences,Beijing 100049,China
Abstract Energetic X-ray radiations emitted from various accretion systems are widely considered to be produced by Comptonization in the hot corona.The corona and its interaction with the disk play an essential role in the evolution of the system and are potentially responsible for many observed features.However,many intrinsic properties of the corona are still poorly understood,especially for the geometrical configurations.The traditional spectral fitting method is not powerful enough to distinguish various configurations.In this paper,we intend to investigate the possible configurations by modeling the polarization properties of X-ray radiations.The geometries of the corona include the slab,sphere and cylinder.The simulations are implemented through the publicly available code,Lemon,which can deal with the polarized radiative transfer and different electron distributions readily.The results demonstrate clearly that the observed polarizations are dependent heavily on the geometry of the corona.The slab-like corona produces the highest polarization degrees(PDs),followed by the cylinder and sphere.One of the interesting things is that the PDs first increase gradually and then decrease with the increase of photon energy.For slab geometry,there exists a zero-point where the polarization vanishes and the polarization angle(PA)rotates by 90°.These results may potentially be verified by the upcoming missions for polarized X-ray observations,such as IXPE and eXTP.
Key words: relativistic processes–polarization–X-rays: galaxies–scattering–radiation mechanisms: nonthermal
1.Introduction
Active galactic nuclei(AGNs),γ-ray bursts(GRBs)and X-ray binaries are the most powerful X-ray objects in the universe.The process of accreting ambient materials and then releasing gravitational energy by the central compact objects is one of the most energetic phenomena in astrophysics.The released energies will eventually heat the accreting gases and result in radiations ranging from radio to γ-rays.The X-rays are widely believed to be produced by the inverse Comptonization of soft photons in the corona which is a hot region close to the central objects (e.g.,Eardley et al.1975;Thorne &Price1975;Haardt &Maraschi1991,1993;Gilfanov2010).Moreover,the soft photons are usually multi-temperature blackbody emissions and come from the accretion disk (Shakura &Sunyaev1973;Page &Thorne1974;Abramowicz et al.1988;Yuan &Narayan2014).
The corona plays a very important role in the disk-corona system.However,the evolution,formation heating and,especially,the geometrical configurations of the corona are still under debate,due to the complicated physical processes involved in the accretion system(e.g.,see the discussions given by Dreyer&Böttcher2021;You et al.2021;Ursini et al.2022).Various physical processes can lead to the formation of a corona and they show similar spectral profiles or spectral energy distributions (SEDs).For example,a corona with an extended slab-like geometry is usually sited above the disk and may be a result of magnetic instabilities(Galeev et al.1979;Di Matteo1998).Materials accreted around a neutron star instead of a black hole will accumulate and finally form a transition layer which shows the characteristics of a corona (Sunyaev &Revnivtsev2000;Long et al.2022).In the vicinity of the black hole,the quite active magnetic processes could release considerable energies by magnetic reconnection which can heat the plasma to a very high temperature (e.g.,Wilkins &Fabian2012).The corona can even be formed by the evaporation of the inner part of an accretion disk,or as the transfer region between the jet and the black hole,either as a failed jet (Ghisellini et al.2004) or as a standing shock wave (Miyamoto &Kitamoto1991;Fender et al.1999;Done et al.2007).The geometrical configurations of these corona models are deeply connected with their physical origins.Thus,distinguishing the geometry of a corona from observable quantities will provide significant constraints on the physics of the accretion system(e.g.,Dreyer&Böttcher2021;Long et al.2022;Ursini et al.2022).
Former researches put some constraints on the geometry of the corona.For example,the size and location of an X-ray corona have been estimated to be within a few gravitational radii by microlensing observations (Kochanek2004;Reis&Miller2013;Chartas et al.2016).Comparing the time lags between the direct and reflected radiations (or radiations in different energy bands)can provide further constraints on the geometrical parameters of the disk-corona system (e.g.,Ingram et al.2019;Mastroserio et al.2021).However,the polarization of X-ray radiations is an alternative and unique way to give possible new constraints on the corona geometry (Dreyer &Böttcher2021;Long et al.2022;Ursini et al.2022;You et al.2021),since the polarizations induced by the inverse Comptonization are intrinsically dependent on the geometry and electron distribution (Schnittman &Krolik2010;Laurent et al.2011;Beheshtipour et al.2017).The Compton scattering can be simply divided into Thomson and Klein-Nishina regimes according to the energy of incident photons and the cross sections are intrinsically polarization dependent (Fano1949;Chandrasekhar1960).It can induce polarizations for anisotropic and unpolarized photons that scatter off non-relativistic electrons (Bonometto et al.1970;Schnittman&Krolik2009).For photons scattering off energetic electrons,the polarization will be suppressed due to the beaming effect (e.g.,Dreyer&Böttcher2021).Thus the polarized radiations among the X-ray bands would be reasonably expected (Poutanen &Vilhu1993;Schnittman &Krolik2010;Beheshtipour et al.2017;Ursini et al.2022)and they can be used as a useful probe to distinguish the geometrical configurations of the corona-disk systems.
Following the previous studies,here we are motivated to provide constraints on the corona geometry by modeling the observed X-ray spectra and polarizations.Our paper is organized as follows.The model and method are introduced in Section2.In Section3,we present the results of our calculations.The discussions and conclusions are finally provided in Section4.
2.Model and Method
In this section,we give an introduction to the model and method used in this paper,which are based on our publicly available code Lemon (Yang et al.2021).Here we mainly discuss how to generate photons effectively in these geometrical configurations for the scattering,and show the estimation procedures.
2.1.The Geometries of the Corona
In this paper,we will calculate the observed spectra and polarizations from three kinds of coronas with slab,sphere and cylinder geometries,respectively.Their geometrical configurations are illustrated in Figures1and2.The slab-like corona is a thin layer and sandwiches the accretion disk completely.Its geometry is determined by the inner and outer radii:Rin,Routand the heightH.The cylinder-like corona is located above the disk with the top and bottom surfaces placed at heightsHandH+Hcrespectively.The radius of the cylinder isRc.As the top surface of the cylinder is set to be sufficiently high,Hcis also very large,thus the effects of its minor changes on the results can be ignored.The corona with a sphere geometry is diagrammed in Figure2,which is described by the sphere with radiusRspand heightHof the sphere center with respect to the disk.
The physical parameters to describe these coronas are the electron temperaturekTe,the number densityneand the optical depth т of Thomson scattering.For the sake of simplicity,bothkTeandnefor all three kinds of coronas are set to be constants throughout the corona.The values of the Thomson optical depth т for three cases are fixed and given by: т=σTneH,т=σTneRc,т=σTneRsp,respectively,where σTis the Thomson cross section.Hence,as т,H,RcandRspare provided,one can calculate the electron number density by and vice versa.

2.2.Photon Generation
For all the configurations,the low energy seed photons are emitted from the standard geometrically thin and optically thick accretion disk(Shakura&Sunyaev1973).We assume that the accretion disk is in a multi-temperature state and its surface temperature changes with the disk radiusR.The distribution function of the temperature is given by (Shakura &Sunyaev (1973),Tamborra et al.(2018))

In order to describe the Keplerian motions of the accretion disk,we define a static reference frame,whose basis vectors are given by ex,eyand ez.With ei,we can further define a local reference frame at radiusRand azimuth angle φ,the basis vectors of which are constructed by

Then with respect to the static reference frame,the Keplerian velocity of the disk atRand φ can be expressed as


whereDm=1−Ω·Vk/c.Notice that the quantities related to the Lorentz transformation are defined with respect to the framegiven by Equation (4).Using Equation (5),the above equations can be written explicitly as

In our former paper(Yang et al.2021),we explained that the Monte Carlo radiative transfer is actually equivalent to the evaluation of the Neumann solution of the radiative transfer equation.Each term of the Neumann solution is a multiple integral which can be written as

wheren(P0) is the number density of the emitted photons and related to the emissivityj(P0)throughn(P0)=j(P0)/hν.Herehis the Plank constant,K(P→P′) is the transfer kernel,f(Pm)is the recording function andP=(r,Ω,ν),which are the position and momentum vectors and frequency of the photon,respectively.The generation of photons is actually related to the calculation of the integral in terms ofP0by the Monte Carlo method,which can be separately written as

where a δ-function δ(z) is inserted,since the seed photons are emitted by the disk that is located in the equatorial plane.We assume that ν1≤ν ≤ν2,since for sufficiently small and large frequency ν,the contributions from the blackbody radiation can be ignored.ν1and ν2are free parameters and set to behν1=10−6mec2andhν2=10−2mec2,respectively.For convenience,we introduce a new variableyto replace ν and ν=10y,y1≤y≤y2,wherey1=log10(ν1)andy2=log10(ν2).Then Equation (11) can be rewritten as

To employ the Monte Carlo method to evaluate the above integral,we split the integrand into two parts,one is used as probability density functions (PDFs) forR,φ,μ,φ andy,and the other is used as weight for the integral.ForR,φ andy,we assign them with the PDFs given by

where ξiare random numbers,whose PDFs arep(ξ)=1 and 0 ≤ξ ≤1.From now on,we will use ξ to represent random numbers,unless otherwise stated.WithRe,φeandye,the position vector of the emission site and the frequency of the photon can be obtained as

The sampling of the initial direction Ωe=(μe,φe) is more complicated and will be discussed in the following sections for the three geometrical configurations,respectively.
While in order to discuss the initial weightwini,we suppose that (μe,φe) has already been obtained.Thenwiniequals the remaining part of the integrand of Equation (12),i.e.,

2.2.1.Slab Case
For the slab corona,the procedure is quite simple,since any photons emitted by the disk will enter the corona automatically.We first construct a local triad at reby

2.2.2.Cylinder Case
Comparing to the slab,the sampling procedures of Ωefor the cylinder and sphere cases are more complicated.This is because if we sample the emission direction Ωeisotropically in,the efficiency will be quite low,since many photon samples will miss the cylinder(or sphere)directly.To increase the efficiency,for the cylinder case,we need to get the region formed by the effective directions of the photons in theplane.Here,a direction denoted by Ωeis effective,which means that a photon assigned with this direction can reach the corona eventually.Using the geometrical definitions given in Figure1,we can obtain the region in theplane directly,which is drawn in Figure3.AsRe>Rc(top panel of Figure3)the blue and red curves are the boundaries of this region and their function expressions are stated as

which are the minimum and maximum of the two functions given by Equation(20).AsRe≤Rc(bottom panel of Figure3),the functions of the boundary curves become

2.2.3.Sphere Case
The procedure for the sphere case is similar to that of the cylinder case,but the local triad at reis constructed in a different way by (see Figure2)

In addition,we should construct another triad at redefined through

where the definition of α is shown in Figure2.In this triad frame,all of the effective directions (μ″,φ″) also form a gray region in the μ″-φ″plane(see Figure4).Then we can draw an effective direction(μ″,φ″)isotropically in the rectangle region[−π,π]×[μβ,1] by the following algorithm (for case (a))

Figure 3.The region formed by the effective photon MDs in the φ′-μ′plane of the triad defined by Equation (17) for the cylinder case.The top panel shows the case of Re>Rc and the bottom panel that of Re ≤Rc.The functions of the boundary curves of these regions are stated by Equations (20) and (23).A sample of MDs will be accepted if it falls into the gray region,otherwise it will be rejected.The sampling algorithms are expressed by Equations(21)and(24).The area S(Re) of this region is a function of Re and should be multiplied with wini to regulate the weight.

Figure 4.The same as Figure 3,but for the corona with a sphere geometry.The effective gray regions for panels from top to bottom correspond to the three geometrical configurations displayed in Figure 2.The blue boundary curve in the top panel is defined by Equation (35).


From Equations (26),(27) and (32),one can obtain that

In panel (a) of Figure4,there is a boundary curve plotted with blue color.The expression of this curve can be simply derived.From Figure2,one can see that a photon reaching the corona sphere must satisfy the condition thatpz≥0 andpz=0 yields the boundary curve.Using the expressions ofpzgiven by Equation (34) andp″x,p″zprovided by Equation (33),frompz=0,we can obtain the function of the curve

Finally,we need to update the weightwiniby using the areasS(Re) of the gray region in Figure4and the analytical expressions ofS(Re) for three panels can be obtained as
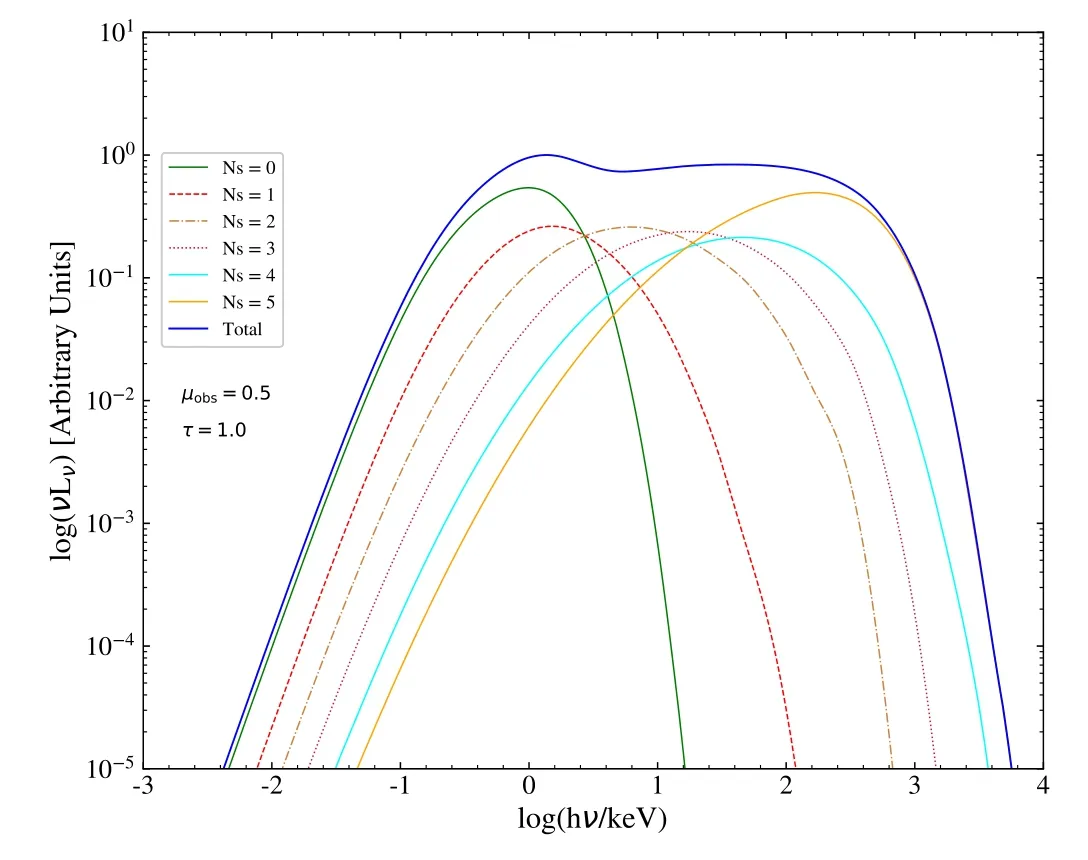
Figure 5.The spectra of a corona with spherical configuration for various scattering numbers.The parameters are:Rin=6.0 rg,Rout=100.0 rg,H=0.0 rg,т=1.0 and kTe=100 keV.

2.3.Scattering Distance Sampling
As a photon is generated,we then discuss how to determine the distance between any two scattering points randomly.As addressed in Yang et al.(2021),the scattering distance is a random variable,and its PDF is given by

Here σa(s)=σa[hν,Te(s)] is the averaged scattering cross section (Hua1997),Te(s) andne(s) are the temperature and number density of hot electrons ats,respectively,Nis the normalization factor and

In our model,we adopt the assumption that bothneandkTe(s)are constants in the corona,then Equation (37) becomes

whereN= 1-exp (-σane sm),which can be sampled by the inverse cumulative distribution function (CDF) method directly.That is
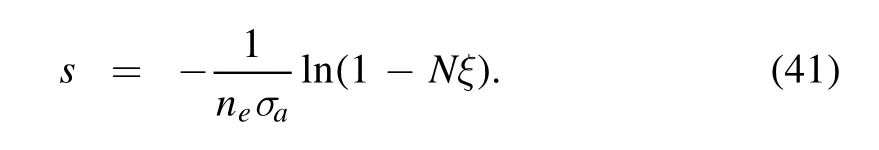
When the scattering distance is determined,the weightwinishould be updated as well by multiplying the normalization factorN,i.e.,wini′=wini·N.
2.4.Scattering Sampling
In our model,we will consider inverse Comptonization of the photons in the three kinds of coronas with the electrons assigned with various distribution functions.As discussed in Yang et al.(2021),Lemon can incorporate any kind of scattering readily.Here,we mainly consider three kinds of electron distributions,i.e.,the relativistic thermal,the κ and the power law distributions,which are respectively expressed as(Xiao2006;Pandya et al.2016)

whereAis the normalization factor.Then the procedure of the method is reported by Schnittman &Krolik (2013)
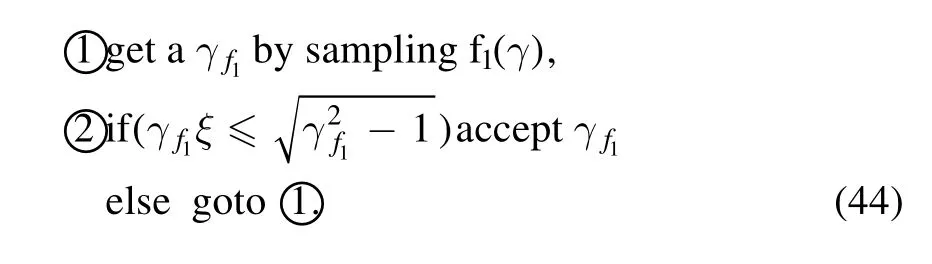
The algorithm of samplingfromf1(γ) is the inverse CDF method,which is equivalent to solving the following algebraic equation (Schnittman &Krolik2013)

whereu=γ/Θ,g(u) = (u2+2u+2) exp(-u),u1=γ1/Θ andu2=γ2/Θ.It turns out that this equation can be solved by an iterative method numerically.To accomplish this,we rewrite the above equation as

whereG0=g(u1)−ξ[g(u1)−g(u2)].Then the rootu0of Equation (45) can be obtained by the following algorithm

wherea=κw−1 andAis the normalization factor.Also one needs to solve the following equation to get a trial sample of γ,

wherea1=κ(κ−1),b1=2aκ,c1=2a2,d1=κ(κ−1)(κ−2)andG0=g(γ1)−ξ[g(γ1)−g(γ2)].The functiong(γ) is given by
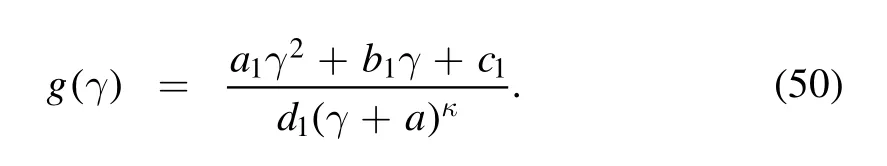
Equation(49)can be numerically solved by an iterative method as well and the algorithm is similar

2.5.Lorentz Transformation of Stokes Parameters
The polarization states are described by the Stokes parameters(SPs):S=(I,Q,U,V)Tand the polarization vector(PV)f.The Compton scattering will inevitably change the polarization states of the photons.In this subsection we will discuss how to describe and trace these changes in Lemon in a detailed way.These discussions,however,can be found in,e.g.,Krawczynski(2012).For the purpose of completeness,we shall provide these descriptions in a more consistent way as follows.


is the rotation matrix (see Chandrasekhar1960).At the same time the PV f has been rotated into the plane of peand k as well.As demonstrated by Krawczynski (2012),Sewill stay invariant under the Lorentz transformation,which means that we can get the SPs in the rest frame of the electron directly as:S=e(from now on,the quantities in the rest frame of the electron are signified with a tilde ˜).The MD (μe,φe) and frequency ν of the incident photon will be transformed as:


2.6.Spectrum and Polarization Estimation
Lemon used a scheme that can improve the efficiency and accuracy of spectrum and polarization evaluations,since the information at any scattering point can contribute to the observed spectrum and polarization.Under the Neumann expansion solution of a differential-integral equation,the scheme is equal to the introduction of a δ-function and recording function(for more detailed discussions,refer to Yang et al.2021).This scheme has actually been applied widely and implemented in many codes dealing with Lyα radiative transfer(e.g.,see Seon et al.2022,where the scheme is named the“peeling-off technique”,also known as“next event estimation”or “shadow rays” (Yusef-Zadeh et al.1984;Laursen &Sommer-Larsen2007;Yajima et al.2012),one may also refer to Whitney (2011) and Noebauer &Sim (2019) for reviews).We will use this scheme to reduce the noise generated by the Monte Carlo method and obtain the results with high signal-tonoise ratio.
Now we discuss the specific procedures of the estimation scheme using the conventions and triads established in the last subsection.The observer is assumed to be located at a direction nobs(μobs,φobs).Due to the axial symmetry of the system,we can choose φobsrandomly,i.e.,φobs=2πξ.Then utilizing the coefficients of the photon and electron triad,we can transform nobsinto the two triads directly by



By the definition of ex(obs),we have assumed that the PA is measured from a direction parallel to the disk in the sky plane.A PV along the north–south direction corresponds to a PA of 90 degrees.This definition is different from the convention adopted by Ursini et al.(2022) with a 90◦rotation.The triad associated withf′obscan be obtained by

3.Results
In this paper we mainly investigate the effects of geometries on the observed spectrum and polarization of the disk-corona system.The corona is assumed to be assigned with a slab,a sphere and a cylinder geometry composed of hot electron gas.In the following,we will present the primary results of our models.
3.1.Example Demonstrations
We first demonstrate the global pictures of the spectra for various viewing angles and scattering numbers.To accomplish this,the values of all other parameters must be fixed.The results are shown in Figures5and6.In Figure5we show the spectra with various scattering numbers viewed at μobs=0.5.From this figure,one can see the typical characteristics for a Comptonized spectrum,i.e.,at high energy bands,the spectrum is composed by a power law followed with a steep exponential high-energy cut-off due to the Klein-Nishina effect (e.g.,Fabian et al.2015;Mastroserio et al.2021).Also as the energy becomes higher,the noise becomes louder.The green line represents the spectrum formed by the multi-temperature blackbody radiations escaping from the disk directly.As the scattering number increases,the corresponding spectrum becomes harder.In Figure6,we show the spectra and polarizations with respect to the inclination angles,where the curves with different colors represent different cosine values of the viewing angles.From the figure one can see that as the inclination angle increases,the PD δ will increase,but the intensityIwill decrease.This is because photons will go through a larger optical depth and thus suffer from more scatterings at higher inclination.

Figure 6.The same as Figure 5,but for different viewing inclination angles.The top and bottom panels are the spectra and PDs,respectively.
3.2.Parameter Settings
The parameters of the disk are set to be the same for the three kinds of coronas(see Table1).The inner and outer radii of the disk are set to beRin=6rgandRout=200rg,respectively.The mass of the central black hole and the mass accretion rate of the disk are 10M☉and 1.4×1018g s−1,respectively.

Table 1Parameter Values for all Simulations
The slab-like corona is composed of parallel planes sandwiching and covering the disk completely (Poutanen &Vilhu1993;Schnittman &Krolik2010).Then,the inner and outer radii of the slab are set to be the same as the disk.The height and temperature of the slab are given byhandkTerespectively.Former researches show that the dependence of results on the heighthis not significant (e.g.,Ursini et al.(2022)).Hence,in all the calculations,we will sethto be 1rg.The Thomson optical depth т of the slab is given asneσTh.We will simulate the cases with т=0.5,1.0 and 2.0.
The geometry of the corona with a spherical configuration is determined by its radiusRspand heightH.For appropriate setting values of these two parameters,the configuration of the corona can either be extended which can fully cover the disk,or compact and located above the disk.Many evidences have shown that the size of the hot corona is most likely very small and close to the central compact object (Fabian et al.2015;Ursini et al.2020,2022),which is the well known lamppost model (Zdziarski et al.1996;Życki et al.1999).In other models,the size of the sphere can be as large as fully covering the whole disk (e.g.,Tamborra et al.2018).Thus in our simulations,we will setRsp=10rgfor a compact configuration andRsp=200.0rgfor an extended configuration.The optical depth т=neσTRspof the sphere is measured from the center to the boundary and set to be т=0.5,1.0 and 2.0 as well.
The corona with a cylindrical geometry is usually used to describe the outflowing materials,or a jet (Ghisellini et al.2004).Then the corona will be assigned with a bulk velocity β=v/c.As long as the motion is not extremely relativistic,its influence on the results will not be significant (Ursini et al.2022).Thus,in our simulations we can set β=0 and focus on the impact of other relevant geometrical parameters on the results.The Thomson optical depth т=neσTRcis measured along the horizontal direction and is also set to be т=0.5,1.0,2.0.The electron temperature is assigned with the value ofkTe=100.0 keV for all the situations.
3.3.Spectra and Polarizations
With the parameter settings and assumptions given above,we carry out the simulations to study the dependencies of observed spectra and polarizations on the geometries of the corona.The results will be presented as follows.
We first present the spectra,PDs and PAs of the radiations emerging from three kinds of coronas.The results are plotted in Figures7,8and9,which affirm that as the optical depth increases,the spectra become harder for all the cases.The profiles of the spectra are similar for the three cases and also for different inclination angles.This supports the perspective of distinguishing the geometries for the coronas with different configurations through fitting the SEDs is not so effective (see also Tamborra et al.2018;Dreyer &Böttcher2021).The polarizations of the three geometrical configurations,however,show significant differences both in the profile and the magnitude.One can see that in the X-ray bands,which we are mostly interested in,the slab corona has the biggest PD,whose value can be up to around 10%depending on the viewing inclination,followed by the magnitude of PD for the sphere and cylinder coronas,which goes to 1%–2%and is less than 1%,respectively.These results are consistent with those given by Ursini et al.(2022).However,in the high energy bands,the results change into the opposite situation,where the cylinder corona has the highest PD up to almost 15%.One can see that there exists zero-points in PDs both for the slab and sphere coronas,as depicted in Figures7and8,where theQcomponent of the SPs vanishes and changes its sign simultaneously.From the parameters in Figures7and8,we can see that both of the two coronas have extended geometrical configurations.This may be taken as a special feature for this kind of corona.
From Figures7and8,one can conclude that the trends and profiles of PD for the slab and the sphere are similar to each other but different from those of the cylinder case.This is because the former two coronas have similar geometrical configurations due to the parameters we chose,i.e.,they both have the extended configurations that fully cover the disk.On the contrary,the cylinder corona has a compact configuration above the disk,which makes its irradiation by disk be less isotropical compared with the extended configurations.For the extended corona,a higher optical depth yields a higher PD,while for the compact corona,the conclusion seems opposite(see Figure9,where the maximum of PD decreases as optical depth increases).

Figure 7.The synthesized spectra(top panels),PDs(middle panels)and PAs(bottom panels)of a corona with slab geometry viewed from various inclination angles.The parameters are: kTe=100 keV and т=0.5,1.0,2.0 for panels from left to right,height h=1.0 rg,and the inner and outer radii of the disk Rin=6.0 rg and Rout=200.0 rg respectively.

Figure 8.The same as Figure 7,but for a corona with sphere geometry.The parameters for the sphere are:the radius of the sphere Rsp=200.0 rg and the height of the sphere center above the disk h=0.0 rg.

Figure 9.The same as Figure 7,but for a corona with cylinder geometry.The parameters for the sphere are: the radius Rc=10 rg,the height H=20 rg and the intrinsic height Hc=100 rg.

Figure 10.The synthesized spectra of coronas with a slab(top panels),sphere(middle panels)and cylinder(bottom panels)geometries for various scattering numbers.The cosine value of the viewing angle is μobs=0.5.Other parameters are the same as those given in Figures 7,8 and 9 for the three kinds of coronas,respectively.
According to our definition of the reference direction of the PA,for all the cases,the PA oscillates around zero and the polarization direction is horizontal in the low energy bands.This result is simply due to the fact that all of the geometrical configurations considered here have axial symmetry,which will yield an orientation of the PVs that can either be horizontal or vertical(Connors et al.1980).However,in the high energy bands,the PA oscillates turbulently which leads the results to become unreliable.
In Figure10,we give the spectra of all configurations for various scattering numbers and optical depths.For the spherical and cylindrical configurations,the profiles of the spectra are quite similar for different optical depths.But for the slab configuration,the spectra become harder as the optical depth increases.
For the corona with a spherical or cylindrical geometry,its heightHmeasured from the disk is an important parameter.The changes ofHwill not only alter the geometry of the system,but also affect the efficiency with which the disk illuminates the corona.For a higherH,the illumination is less isotropical.Hence we do simulations to investigate the impact ofHon the spectra and PDs.The results are plotted in Figures11and12for the spherical and cylindrical cases,respectively.From these figures one can see that asHincreases,the spectra become softer in the high energy bands,due to the reduction of the luminosity and flux that could be captured by the corona.As the viewing angles change,the spectra tend to stay the same.But for the PDs,the magnitude of variations is considerable.Averagely,the PDs of the cylinder corona are bigger than those of the sphere corona.The profiles of the PDs for the two configurations are analogous,due to the quite similar geometrical parameters we choose.However,for the sphere case,with the increase ofH,theQcomponent will change its sign from positive to negative.But for the cylinder case,the sign ofQalways stays negative.Also one can see that with the increase ofH,the PDs in the low energy bands stay almost unchanged,just as the trend of the spectra.However,the changes of the PDs in the high energy bands are significant.This difference of PDs between the low and high energy bands may be used as a probe to discriminate a corona with or without a compact geometry.

Figure 11.The spectra (top row panels) and PDs (bottom row panels) of a corona with a sphere geometry for different heights H and viewing angles μobs.The parameters are:the radius Rsp=10.0 rg,optical depth т=1.0 and temperature kTe=100 keV.The height H of the spherical center varies from 10.0 to 80.0 rg and the corresponding results are plotted with different colors and line styles.The cosine values of the viewing angles μobs are 0.2,0.5 and 0.9 for panels in the left,middle and right columns,respectively.

Figure 12.The same as Figure 11,but for a corona with cylinder geometry.The parameters are: the radius Rc=10 rg and intrinsic height Hc=100 rg.
4.Discussion and Conclusions
The geometrical configurations of the corona in an accreting systems are poorly understood due to the degeneracy of spectroscopy differentiating the system.Polarimetry provides a more effective and powerful option to overcome this dilemma.With the advent of the missions IXPE (Weisskopf et al.2016)and eXTP (Zhang et al.2016,2019),the era of high-quality data from polarization observations will arrive in the near future.Hence it is necessary and urgent to do the theoretical studies in advance.For this purpose,we carry out simulations of radiative transfer in the corona with different geometries.These simulations are based on the publicly available Monte Carlo code,Lemon (Yang et al.2021),which is based on the Neumann series expansion solution of differential-integral equations.By using the code,one can increase the signal to noise ratio dramatically and simplify the calculations when the configuration of the system has geometric symmetries.The main contents and results of this paper can be concluded as follows:
We have discussed detailedly how to simulate the polarized radiative transfer in the three geometry configurations,namely,the slab,sphere and cylinder.We emphasized how to generate photons efficiently for the sphere and cylinder cases.To accomplish this,we have derived the shapes of the regions formed by the effective MDs in the φ-μ plane of the triad.This method can increase the efficiency of the simulation,especially for coronas with a compact geometry,since the solid angle subtended by the corona with respect to the emission site is small,which further reduces the probability that a photon can be received by the corona.In our model,we considered the effect due to the Keplerian motion of the disk on the spectra.This effect works by affecting the photon generation.In our model,it can be taken into account readily through a Lorentz transformation,which connects the emissivities in the comoving reference frame of the disk and the static reference frame.The Keplerian motion of the disk will make the frequencies of the seed photons have blue or redshifts,which will further affect the final results.While due to the low speed for most parts of the disk (R≫1),the Keplerian motion seems to have a minor impact on the spectra and polarizations.However,if we focus on the radiations emitted from the most inner part of the disk,both the Keplerian motion and general relativity effects should be taken into account.Then we discussed how to obtain the scattering distance between any two scattering sites by the inverse CDF method.Because the electron distribution has a very important impact on the Comptonized spectra,we proposed a new scheme to deal with three often used distribution functions,i.e.,the thermal,κ and power law,in a uniform way.Next,we demonstrated how to implement the polarized Compton scattering in the Klein-Nishina regime consistently and detailedly,which involves complicated triad constructions,Lorentz boosts,SP transformations and rotations.Finally,we discussed the procedure for evaluating the contributions made by any scattering site to the observed quantities when the inclination angle of the observer is provided.
We use our model to simulate the radiative transfer in three kinds of coronas with different geometrical configurations.The results demonstrate that the polarizations of the observed radiations are significantly dependent on the geometries of the corona.Different configurations will produce PDs with different magnitudes and profiles in the X-ray bands.The corona with an extended configuration,such as the slab,yields a higher PD while the compact one yields a less polarized result.With the increase of the photon energy,the PD will increase gradually as well until a maximum is reached.After that,the PD will decrease to zero due to the relativistic beaming effect (Dreyer &Böttcher2021).The maximum of PD for the extended configurations increases with the increase of the optical depth,but for the compact configurations the conclusion is the opposite.
Our results are consistent with those of the former researches.However,our model and code are flexible and can deal with different geometrical configurations readily.One just needs to modify the photon generation and tracing parts.However,the results presented here are quite theoretical and not connected with practical observations.Also,our model does not include the effects of general relativity,which inevitably plays an important role in the radiative transfer around a black hole.These effects will be included in the future work.Nonetheless,our model includes the essential ingredients of Comptonization in a hot electron corona.Thus,hopefully,our model will provide some useful insights for the observations of upcoming X-ray missions,such as IXPE and eXTP.
Acknowledgments
We thank the anonymous referee for helpful comments and suggestions that improved the manuscript significantly.Y.X.L.thanks Zhang Guo-bao for kindly allowing us to use his personal workstation.We also thank the Yunnan Observatories Supercomputing Platform,on which our code was partly tested.We acknowledge financial support from the National Natural Science Foundation of China (NSFC,Grant Nos.U2031111,11573060,12073069,11661161010 and 11673060).
Code availability:The source code of this article is part of Lemon and can be downloaded from:https://bitbucket.org/yangxiaolinsc/corona_geometry/src/main/.
 Research in Astronomy and Astrophysics2022年8期
Research in Astronomy and Astrophysics2022年8期
- Research in Astronomy and Astrophysics的其它文章
- A Baseline Correction Algorithm for FAST
- Ultra-wide Bandwidth Observations of 19 Pulsars with Parkes Telescope
- Correlation between Brightness Variability and Spectral Index Variability for Fermi Blazars
- Candidate Eclipsing Binary Systems with a δ Scuti Star in Northern TESS Field
- HI Vertical Structure of Nearby Edge-on Galaxies from CHANG-ES
- Analyzing Dominant 13.5 and 27day Periods of Solar Terrestrial Interaction:A New Insight into Solar Cycle Activities
