Irregular Spatial Distributions of Spectral Line Parameters in the Middle Solar Chromosphere Revealed from Analysis of Solar Flash MgI b2 Spectra

Yuhang JinZhongquan QuZhi XuGuangtao DunLiang ChangXiangming ChengXiaoyu ZhangLinhua Dengand Yang Peng

1 School of Astronomy and Space Science,University of Chinese Academy Sciences,Beijing 100049,China; zqqu@ynao.ac.cn

2 Yunnan Observatories,Chinese Academy of Sciences,Kunming 650216,China

Abstract This paper presents the analytical results of solar Mg I b2 flash spectra,obtained by the prototype Fiber Arrayed Solar Optic Telescope in process of the 2013 Gabon total solar eclipse.The analysis reveals irregular distributions of the spectral line parameters like ratio of line source function to continuum one β,ratio of line emissivity to continuum emissivity ζ,ratio of the continuum opacity to the line opacity r0,line center optical depth т0,the line width ΔλD,and the line-of-sight velocity vlos,while the approximately spherical symmetry can be found in the maps of integrated line intensity and continuum intensity.These irregular distributions originate from those of line profile features like the maximum intensity,the line width and line center wavelength.It is also found from the recovered line center optical depth т0 that in the middle chromosphere,the optical depth is not small due to nonignorable absorption and the long light path along the line-of-sight.Finally,we show that the excessive broadening of spectral lines can be due to co-existence of multiple radiative sources with different line-of-sight velocities unresolved in one detector pixel.

Key words: Sun: atmosphere–Sun: chromosphere–Sun: fundamental parameters

1.Introduction

The solar atmosphere consists of photosphere,chromosphere,transition region and corona.The brightness of the photosphere prevents us generally from observing the outer layer of the Sun’s atmosphere.Solar eclipses provide us direct off-limb observation but side view of these layers which host the visible solar activities especially eruptions like flares,filament eruptions and CMEs.Furthermore,abnormal heating of the chromosphere and corona remains a big mystery to human beings.Researchers want to make clear the mechanisms responsible for the heating for a long time.However,first of all,the real thermodynamic conditions should be checked exactly so that we can evaluate the interesting thermodynamical parameters like the spatial distribution of real kinetic temperature and the density,and thus the total heat capacity in these regions.

The solar chromosphere was first photographed during a total solar eclipse in 1860 by Secchi(1860).The first luminous spectra were observed in 1871 (Young1871),which is primarily the emission spectrum of the chromosphere.In 1973 Vernazza et al.(1973)presented the formation regions of various spectral lines and continuous spectra.Spectral analysis can help us quantitatively to probe the physical quantities via measuring its features and/or fitting spectral line profiles.It is also possible to extract the physical quantities at the corresponding formation heights in each wavelength interval(Qu &Xu2002;Leenaarts et al.2012).For instance,the information on,such as galaxy evolution,including excitation sources,metallicity,ionization parameters,pressure,electron density,and so on,of the different heights can be recovered by analyzing emission lines of different elements (Kewley et al.2019).However,the diagnostics should be strictly checked.For instance,it is a common knowledge in the literature that the line width can be used to diagnose the kinetic temperature(Cauzzi et al.2009) if the microturbulent is known or reasonably assumed.But we will see,the width is not a good candidate for the diagnostics if a strong non-thermal broadening is present.Ding &Fang (1992) and Fang et al.(1993)diagnose the Doppler frequency shift and asymmetry of the flare spectral line,and get the information about the distribution of the velocity field.

In general,the spectra form in a vast range of scales via the interaction of radiation with matter.In solar intermediately high atmospheric layers like the middle chromosphere which are not optically transparent,the radiative transfer process should be taken into account.The radiative transfer (RT) equation(Mihalas1978),(Equation (1)) in form of a differentiation is the basis of complete spectral analysis.

In order to disentangle the radiative transfer,some specific techniques are accepted,e.g.,linearizing the radiative transfer equation (Auer &Mihalas1969).Otherwise,the temperature correction method (Kurucz1970) and the Λ operator method(Werner1986) are often used.However,though the later method can deal with more spectral line blending,it has poor convergence property and stability in iterative calculation.An alternative method combines the advantages of the two abovementioned methods,i.e.,linearizing the radiative transfer equation first,solving it separately and iterating with each other.It is a common sense that non-LTE radiative transfer problem is one of the most difficult problems in solar physics because it involves nonlinear coupling between radiative field and particles with many excited states.Currently,most radiative transfer problems are solved by accelerating/approximate Λ iterative methods.A broad class of numerical methods have been developed by these methods.They combine some approximations with operator perturbation techniques to speed up the simplest Λ iterative process to solve radiative transfer and statistical equilibrium equations (SE) in turn (Kuzmanovska-Barandovska &Atanackovic2010).Lites et al.(1988)and Liu et al.(2021) proposed methods of inversion of observed spectral lines,which are very enlightening to the present investigation.It is noteworthy that all these abovementioned methods are generally used for analyzing the spectral data acquired on the solar disk.

In general,researchers adopt an assumption of Local Thermodynamic Equilibrium (LTE) atmosphere model,which is used to approximately disentangle the issue of Non-local Thermodynamic Equilibrium (Non-LTE).In LTE,the following conditions stand in the local region:the intensity of thermal radiation is uniform and isotropic,and can be described by the Planck function;the relation between emissivity and opacity satisfies Kirchhoff’s law;the electron velocity distribution obeys Maxwellian velocity distribution law;the excitation and ionization of atoms can be described by Boltzmann’s formula and Saha’s formula Mihalas (1978).As the particle density decreases with height,physical conditions in the chromosphere,transition zone and corona deviates gradually from the LTE due to decrease of the particle collision rate.If the deviation is small enough,the LTE can be used as an approximation.However,Mihalas(1978)pointed out in 1978 that even a small deviation from the LTE would lead to a non-negligible error in the diagnosis of early star abundance.Therefore,the quantitative evaluation of the departure from the LTE is very valuable for precise diagnosis of the physical conditions in the solar middle and upper atmosphere.

In order to determine the overall physical state of atmosphere,the distribution of particles under different excited and ionized states should be known.Researchers often apply a departure factor to quantitatively measure extent of the deviation.Mihalas(1978)presented the definition of traditional departure factor in 1978.γ=Hereniindicates the occupation number of energy leveliunder the Non-LTE,while asterisk*represents the value under the LTE condition.It is easily noticed that if the LTE is achieved,the γ should be unit.The further the γ value departs from one,the further the condition is away from the LTE.On the other hand,both emission and absorption of the line and continuum depend on the occupation number.Therefore,the ratio of the line emissivity to the continuum one,or the ratio of the line opacity to continuum opacity can reflect the departure.Researchers like Vernazza et al.(1981),Anderson &Athay(1989),Qu et al.(2006) have defined another factor and made more specific and effective treatments in further studies.

It is easily understood that the selection of specific spectral lines as probers is important for the diagnostics.In the visible band,Na I D lines,K I resonance line (Quintero Noda et al.2017),Mg Ibtriplet,He I d3 587.6 nm line and Mg I 457.1 nm line (Langangen &Carlsson2009) are profitable candidates to probe physical information of the middle,upper photosphere and lower chromosphere when these lines take a form of absorption.However,when they become emission lines,their formation heights will become greater.This requires a great amount of involved atoms staying at the upper level with excitation potential higher than the lower level to make the emission lines observable.Without sufficiently large particles of high energy state distribution,the source function is too small to produce detectable emission lines.In this point of view,many emission lines can be suitable to study the physical conditions of the chromosphere.For instance,the magnesiumbtriplet is produced by transitions of the same energy level with total angular momentumJu=1 to three different lower levels withJl=0,1,2 respectively.The excitation potential reads as 5.11 eV (fromhttps://www.nist.gov/pml/atomic-spectradatabase),and their formation temperature can be derived approximately to be 3.94×104K after directly applyingEk=3/2kT,wherekstands for Boltzmann constant andTthe temperature in Kelvin (Liu et al.2021).Thus it becomes clear that the emission of the Mg Ibline above the solar limb is typical of 104-105chromospheric plasma.

Finally,it is profitable for researchers under the good probing condition.A solar eclipse,especially a total one,provides a unique chance for studying the physical conditions of the middle and upper atmosphere,since the pollution from illumination of the solar photosphere and scattering due to the telluric atmosphere becomes much less than normal groundbased observation.Data of two-dimensional flash spectra obtained by the prototype Fiber Arrayed Solar Optic Telescope(FASOT) (Qu2011) will be used here for the diagnostic purpose.From analysis of these data,spatial distribution of spectral line parameters can be quantitatively extract.

2.Observations

A total solar eclipse is a rare opportunity to study the middle and upper solar atmosphere.The analyzed data were obtained during the 2013 Gabon total solar eclipse.The observation was carried out at Bifoun town,Gabon.The totality began at 14:54 p.m,2013 November 3,and lasted about a minute.It aimed originally at spectropolarimetry of emission lines by the prototype Fiber Arrayed Solar Optical Telescope(FASOT)(Qu et al.2017).It shows that solar eclipse observation is still a scientific requirement (Pasachoff2009).FASOT (Qu2011) is equipped with a pair of integrated field unit (IFU) for precise spectropolarimetry of spatial points within Field of View(FOV) of two-dimensions.Before the present polarimetry,Kuhn et al.(2007)applied a single IFU to solar observations in 2007.In order to see clearly the observational configuration,we depict Figure1for illustration.It indicates that the measured intensities are results from integrations over a vast region along the line-of-sight above the photosphere.In the top-right corner,the alignment of the fiber(and thus the spatial sample points in the two-dimensional FOV)is shown.Figure2presents the IFU FOV location relative to the solar crescent.

Figure 1.Configuration of observation by the prototype FASOT during a total solar eclipse.The lenslet array of the IFU is coded and illustrated in the top-right corner.

Figure 2.Position of the field of view of the IFU.The bright crescent is the remaining part of the Sun occulted by the moon,and the white square indicates the position of IFU field of view relative to the crescent.

The sample flash spectra were acquired before and after the totality in 516–532 nm band(Qu et al.2017),which contains a large number of spectral lines including neutral magnesiumbtriplet (Mg Ib1518.4 nm;b2517.3 nm,andb4516.7 nm)forming in the middle chromosphere,and once ionized iron line(Fe II 531.7 nm) also forming in the chromosphere (Ding &Habbal2017),as well as the well-known green coronal line(Fe XIV 530.3 nm).Twenty-five spatial sample points coded from 0 to 24 in the top-right part of this figure are recorded from the pair of 5×5 lenslet array as heads of the IFUs as shown in Figure2.The image of raw data named Eclipse Polarimetry (EP) is shown in Figure3.There are totally 50 spectra which can be divided into two groups in the upper and lower parts respectively.The 25 spectra of the lower group,indicated by “eo”,and the 25 spectra of the upper group,indicated by “oe”,produced by a Savart plate,come from the same solar region but with the opposite polarization modulation states.

The EP data were acquired with exposure time of the 8.0 s two minutes later than the totality.The dispersion is along the horizontal direction,with a dispersion of 0.0122 nm pixel-1,and the actual spectral resolution reads as 0.0732 nm@519.25 nm.In the upper half frame,25 sample spatial points produces 25 spectra of 1/2(I-Q) intensity for each spectrum,where StokesIandQindicate respectively the total radiative intensity and the linear polarization intensity,and the lower half frame 25 spectra with intensity of 1/2(I+Q)with the opposite polarization state.Therefore,the radiative intensities are sums of the intensity of the pairs respectively after the dark current and flat field reduction.One typical emission spectrum is depicted in Figure4,where the intensity is in unit of readout from CCD detector.It is worth noting that each spatial sampling point covers 2″,corresponding to a spatially projected scale of about 1500 km in the sky plane.A raw image of absorption spectrum,named EP0,acquired at the disk center before the eclipse is shown in Figure5for instrument profile calibration as described in the following section.Finally,the intensities are measured in units of the detector readout throughout the paper.

Figure 3.Image of raw data of polarimetric spectra obtained just after the totality.We named them EP.The exposure time for this frame was 8.0 s.The observational band ranges from 516.3 nm to 532.6 nm.Note that intensities of the 25 spectra(corresponding to 25 spatial points)are 1/2(I-Q)produced by“oe”pair in the upper part and those of the lower 25 spectra are 1/2(I+Q) by “eo” pair (Qu et al. 2017).

Figure 4.One sample spectrum of the emission lines.It is named EP.Intensity is in units of readout from CCD detector.

Figure 5.Absorption spectrum data measured at the solar disk center before the solar eclipse,named EP0.

3.Data Reduction and Spectral Analysis Methods

In this section,we describe the data reduction including the dark current,flat field and especially the instrumental profile calibration,and then present the analytic solution to the radiative transfer equation used to extract information on the spectral line parameters.

3.1.Data Reduction

As is well known,the spectral data can be applied only after suitable reduction.It is normal and simple to calibrate the dark current and do the flat-fielding.The latter operation is carried out after the binning at each wavelength point for each spectrum covering 4–5 pixels along the vertical direction (see Figure3).Then the instrumental profile should be calibrated because it causes unreal additional profile broadening.It is a common knowledge that the data obtained by an instrument are the result of convolution of the instrument profile,the corresponding deconvolution is necessary.In order to finish it,we simulate the convolution with a method based on that used by Valenti et al.(1995) and improved according to the particularity of the prototype FASOT data.Valenti et al.(1995)utilized a broad-width central Gaussian function and four to eight satellite Gaussian functions to construct the instrumental profile.They convolved the constructed instrumental profile with the standard spectrum,and then compared the result with the observed spectrum.By comparison,they continued to adjust the free parameters of the instrument profile until a satisfactory agreement is achieved,and then the corresponding instrumental profile is obtained.Based on this method,we conduct the calibration operation in the way described below.

1.In the sub-band range 516.23–518.70 nm concerned,spectra recorded in atlas obtained from the Fourier spectrometer of the National Optical Solar Observatory of the United States are used as the standard solar data.A set of spectral data(EP0) obtained by the prototype FASOT at the disk center before the solar eclipse is selected for the comparison.

2.According to Valenti’s method,we construct an instrumental profile with three Gaussian functions: a central Gaussian function and two satellite Gaussian functions (see Figure6).

3.Blind deconvolution of the disk center spectra observed by the prototype FASOT is performed using the instrumental profile.When the result of blind deconvolution approaches the standard solar spectrum to a satisfactory degree after adjusting the free parameters in the functions describing the instrumental profile,a reasonable instrumental profile (Figures6,7) can be obtained.In this way,the half-width of the instrumental profile is found to be about 0.06 nm.

After this operation,we use the instrumental profile to conduct the blind deconvolution for the EP data.Figure8presents the comparison of spectral data obtained at “point 0”P0 and the result after blind deconvolution.

Figure 6.The instrumental profile obtained from the comparison with the standard solar spectra.

Figure 7.Comparison among the blind deconvolution(blue line),the disk center data in the quiet Sun region observed by the prototype FASOT(red line)and the FTS data (black line).

3.2.Radiative Transfer Equation and its Solution

During the solar eclipse observation,emission line spectra formed in the middle and upper atmosphere of the Sun were acquired including the magnesium triplet,among which theb2line is selected for simulation.It should be kept in mind that the atmospheric layers are not optically thin for these middle atmospheric lines along the line-of-sight,as will be evidenced by the fitting,and the background is not the photosphere.According to universally used accelerating/approximating Λ iteration method (Kuzmanovska-Barandovska &Atanackovic2010),we prefer the inversion method proposed by Lites et al.(1988) described by Liu et al.(2021) in detail.

The radiative transfer equation of the spectral line is generally written as

HereIis the radiative intensity,zis the geometric length measured along the observer’s line of sight,κ=κc+κl0φ is the total opacity,a sum of the continuum opacity κcand line center opacity κl0multiplied by the profile φ,j=jc+jl0φ=κcSc+κl0Slφ is the total emissivity containing the continuum onejc=κcScwithScbeing the continuum source function,and line onejl0=κl0SlwithSlbeing the line source function.

Now,because we concern the average along the line-ofsight,it is suitable to make the following assumptions:

1.In the formation region where the magnesiumb2line is formed,i.e.,middle chromospheric layers,the scattering does not play a crucial role thus is not taken into account for simplicity.Only the emission and absorption are included in calculation;

2.In the middle chromosphere,radiative damping for the Mg Ib2line is small because the collision broadening is small,witnessed by the fact that the far wings of the emission line are almost invisible,a contrast is seen by comparing the emissionb2line in Figure3with the corresponding absorption one shown in Figure5where the damping is evident.We approximate theb2line as a Gaussian one symmetric about the line center;

Figure 8.Emission line data for instrumental profile calibration from EP at “Point 0”,P0.The black line indicates the raw data while the red one is the deconvoluted data.

3.Since emission spectra measured are integrations of column extended along the line-of-sight,the continuum source functionSc,line source functionS1,the ratio of the continuum opacity to line opacityr0,the line center wavelength λ0,the Doppler width ΔλDare assumed to be constants.

According to the second assumption,the line profile φ is approximated by a Gaussian one.When the thermal motion velocity of atoms satisfies the Maxwellian distribution(Equation (2)),for a special direction x (say,the line-of-sight direction):

wherev0is the average velocity of the particle,andvxits thermal motion speed along the line-of-sight.It is easily demonstrated that the Gaussian profile is related to the velocity distribution under the LTE as follows.If absorption/emission takes place at λ0,when an absorber/emitter moves atvxspeed,due to the Doppler effect,the absorption wavelength becomes λ=λ0-λ0vx/c.After defining the Doppler width as ΔλD=λ0v0/c,the line profile formed from all particles obeying the Maxwellian distribution should be

In the above equation,λ0,obsindicates the line center wavelength to be determined.

Now,settingr0=κc/κl0,anddт0=-κl0dz,where the geometric scale of light pathzis measured along the line-ofsight,Equation (5) is rewritten as

Its integral formal solution is

In case of eclipse observation,it is easy to present the boundary condition.When т0=0.0,there is no radiation from the outside of the Sun,thusI(т0)=0.0,and this leads to from the above assumptions that the line parameters are constant along the line-of-sight

Since the continuum intensity is measurable,and its radiative transfer equation reads as

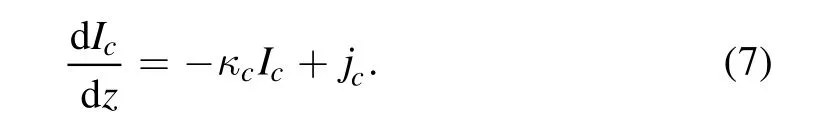
can be solved after these above-mentioned assumptions under the boundary condition that When т0=0.0,Ic=0.0,

It is convenient for us to fit the line intensity profile normalized by the continuum.Thus

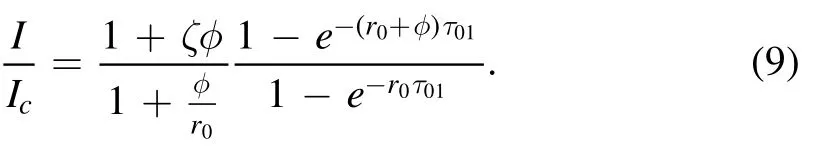
In the above equation,ζ ≡β/r0=jl0/jc,i.e.,the ratio of the line emissivityjl0to continuum emissivityjc,and β ≡Sl/Scdefined by Qu et al.(2006).Equation(9)becomes the theoretical basis for numerical fitting in the following.In the above equations,there are five free line parameters to be determined,i.e.,ζ,r0,т01,as well as λ0and ΔλDcontained in the profile φ (see Equation (3)).ζ=(Slκl0)/(Scκc)=jl0/jcis the ratio of the line emissivity to the continuum spectrum emissivity.That is what we get from Equation (10).

The line-of-sight velocityvlosrelative to the quiet Sun region can be deduced by the following familiar Equation (11).

Whereascis the light speed,λ0,losthe line center wavelength measured from the quiet Sun region at solar disk center before the eclipse.λ0,los=517.2935nm.

When considering the microscopic turbulent velocity,expression of the Doppler width becomes

In general,the“effective kinetic temperature”is derived in this literature from Equation (13):

wheremis the mass of radiating atoms or ions,andvtis the microscopic turbulent velocity.Generally,vtis a function of the coordinates.However,for simplicity,we accept an average value of 4.60 km s-1from Model C proposed by Jevremović et al.(2000),in the height range of 500–2000 km from the temperature minimum region to the middle chromosphere.However,the “temperature” should be carefully re-interpreted in these layers that there are multi-components in the line profiles,as pointed out below.

A code named Curvefit in IDL software package is used to fit the emission line profiles in order to get information on the line parameters of the neutral magnesiumb2line.The Curvefit function uses the gradient extension algorithm to perform nonlinear least-square regression.The following points should be noticed:

a.The number of sample wavelength points within the Mg Ib2line is more than eight,thus more than the number of free parameters to be fitted;

b.The normalized intensityI/Icis fitted rather than line intensity itself.Thus the solution expressed by Equation (3)becomes the merit function;

c.In order to obtain more reasonable fitting results and make the iteration faster,the iterative process begins from the initial values,referred to Lites et al.(1988)’ work;

In the actual simulation,we tried first fitting involved with these five free parameters(ζ,r0,т01,λ0and ΔλD).However,it is found that some parameters cannot essentially be changed by the iteration even we input an initial value greatly away from the model one,thus we have to fix them and get their values in another manner.After trials,the number of the free parameters is reduced to three (ζ,r0and т01).The two parameters λ0and ΔλDare extracted from direct measurement of the Full Width of Half Maximum(FWHM)and the wavelength position of the maximum intensity of the cubic spline interpolated profile based on the observational one,as demonstrated in Figure9whereP0of the EP is taken as an example.The Doppler width of the spectral line can be obtained from measuring the FWHM and using the relationHowever,it is worth noting that if the absorption is present in,say,line wings,like the situation in Figure11below,the Doppler width may be underestimated.In this way,the fitting iteration process becomes much more stable and convergent to the reasonable values.It is noteworthy that in the far spectral line wings,the normalized intensities are less than unit,which means the absorption remains there,and emission does not become complete over the whole line.This is a feature of the middle chromosphere probed by the neutral magnesiumb2line.Here we show one set of fitting effects as an example (Figure10).

Following the above-mentioned process,we perform fitting for twenty-five points of the EP.Four optimum fittings are shown in Figure11where the fact that the different line parameters come from the different profile is demonstrated,and for the two points symmetric to the solar radius (diagonal line in the square of FOV from the upper-right point to lower-left one),their intensity profiles are very different,and thus the asymmetric distribution of the line parameters is shown in the case.

Figure 9.The measurement of line center wavelength and line width of Mg I b2 line 517.3 nm from EP at P0.The dots represent observational data,and the width between two interpolated red dots,whose intensities are same as half of maximum intensity,reflects the Full Width of Half Maximum (FWHM).The histogram presents the intensity integration over the line.The pink curve represents the interpolated profile to obtain these two parameters.The two parameters measured at P0 in this way are : λ0=517.277 nm,ΔλD=0.0211 nm.It is noteworthy that at far line wings,the spectrum remains absorption.

Figure 10.Fitting result at 517.3 nm Mg b1 from EP at“Position 0”.The dots is the observational data,and the line is the fitting curve.The spectral line parameters obtained are: ζ=4.56, r0=2.64×104,т01=0.77.

Figure 11.Fitting results at Mg I b2 517.3 nm line from the EP.In the left panel,two fitting cases at P2(black)and P21(red)are depicted of those profiles from which a great difference of the recovered line parameters.This shows that the difference comes from different profiles.In the right panel,the fitting result of two points P3(black)and P15(red)symmetric to the solar radius is shown.This is one of cases indicating the asymmetric distribution.The dots represent the observational data,and the black lines are the fitting curves.The spectral line parameters obtained are in Table 1.

4.Distributions of Line Parameters Deduced by Spectral Analysis

After trials of fitting Mg Ib2line intensity profiles,we select one frame named EP for discussing the fitting results below.

Table1lists with the spatial point code in the leftmost column,the integrated line intensity shown in Figure9,adjacent continuum intensity and their ratio in three left columns.It is worth noting that the integrated line intensity is obtained over a wavelength interval from 517.22 to 517.34 nm.Dimensionlessis calculated withfrom multiplyingIcby the wavelength interval width,as listed in the table.Icis still the value that we use to normalize in data processing.The line parameters recovered from the fitting β,ζ,r0are listed in the middle columns,while λ0,ΔλDderived from the profile feature measurement are shown in the right columns,along with the so called “effective temperature ‘T” derived from the Doppler width according to Equation(13)under the assumedvtof 4.60 km s-1,listed in the rightmost column.It should be pointed out thatvlosmeasures the Doppler displacement of the line center from the line center wavelength averaged over 25 spatial points in the quiet Sun region at the disk center before the solar eclipse,thus it reflects the relative velocity.For the neutral magnesiumb2line,the average wavelength reads as 517.2935 nm.Three aspects are attractive to us.One is the relevant values between the ratio of the integrated line intensity to the continuum one and the recovered ζ,the ratio of the line emissivity to the continuum one.This specifies that the emission plays the dominant role in the line formation though the absorption can be seen in far line wings.Another aspect is noted that the line center optical depth т01is not much less than unit,or the atmosphere along the line-of-sight is not optically thin.This can be understood from the fact that the absorption remains non-ignorable,as witnessed in the far line wings,and the light path along the line-of-sight is great.The last one is the abnormally higher “effective kinetic temperature”,deduced directly from the line Doppler width,which ranges from 1.39×105to 1.86×105K,greater than the formation temperature 3.95×104K mentioned above by one order.According to these recovered “effective kinetic temperatures”,theb2line would form in the transition zone.This conflicts with our common knowledge.To solve this problem,we need to think in two aspects.On one hand,an issue is raised that whether the broadening is completely caused by thermal motion.On the other hand,whether the thermal broadening is shaped by the Maxwellian distribution of thermal motion particles remains questionable.For the latter aspects,many researchers demonstrated that Maxwellian distribution cannot be the general distribution.For instance,Dudík et al.(2014) presented the distribution of non-Maxwellian κ distribution to diagnose the degree of departure from the Maxwellian distribution,and then Dudík et al.(2017)demonstrated that the transition region line profiles can be better fitted with non-Maxwellian κ distribution which increases the non-thermal broadening.In the present paper,we emphasize the non-thermal broadening.

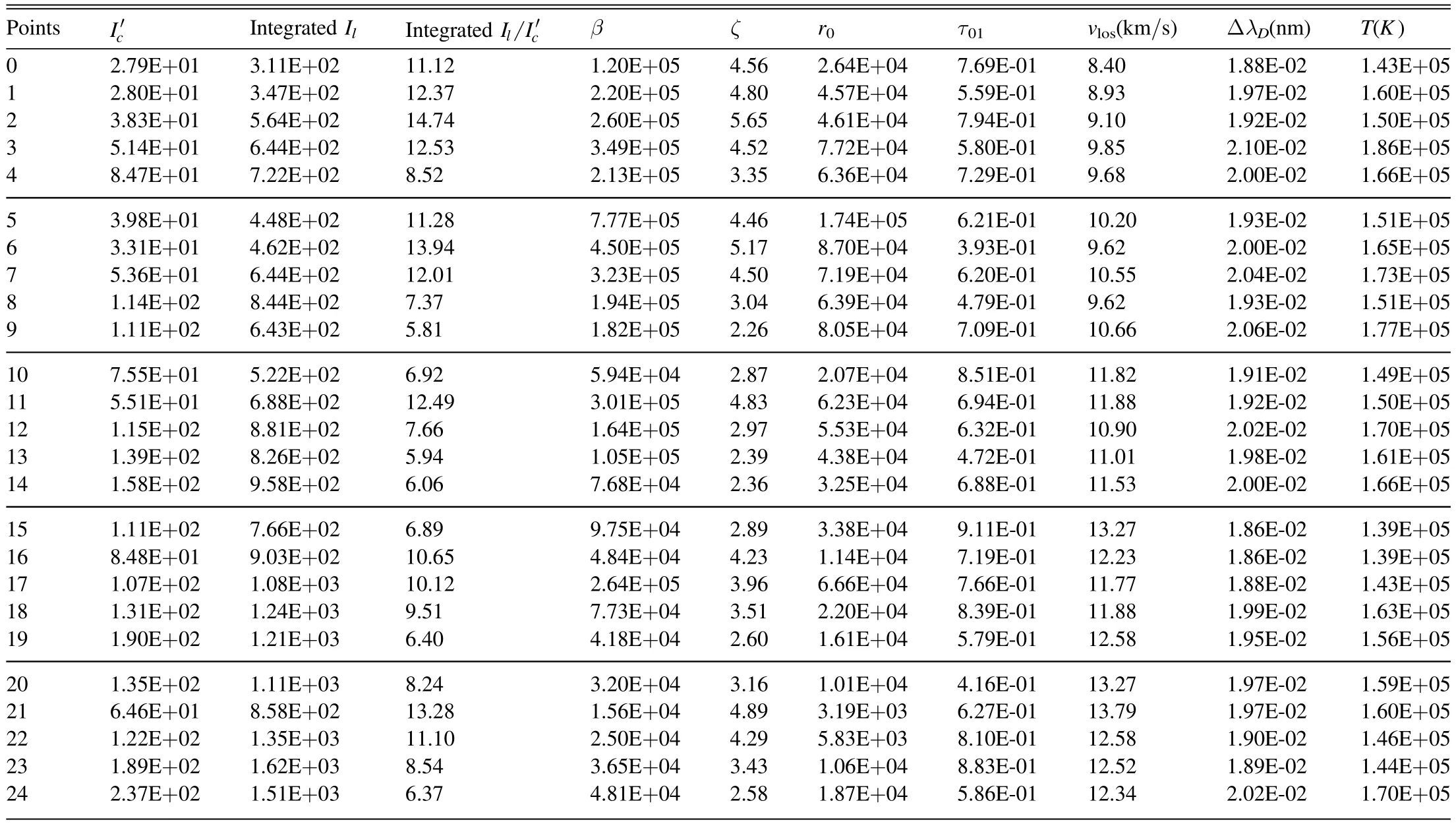
Table 1The Measured Intensities and Fitting Results of Mg I b2 517.3 nm line in EP Data

It is noteworthy that each spatial pixel of the prototype FASOT covers about 1500 km in the sky plane.Therefore,the spectral profile observed at each pixel can be contributed from multiple individual sources that cannot be distinguished.One cannot expect that these sources have the same line-of-sight velocity.This causes inevitably the observed spectral line width to abnormal values.In order to illustrate this case,we adopt three individual sources as examples to illustrate the spectral line broadening.The three profiles of these radiative sources are calculated with parameters close to those in1.It isnoteworthy that only a qualitative demonstration is shown here for the non-thermal broadening.Figure12is depicted for the calculation result.The blue dotted and black lines are produced with the formation temperature 3.95×104K,but with large different line-of-sight velocities.The red line is the synthesized profile normalized by the continuum intensity again.For comparison,we plot the actually observed profile as the green curve.It is easily witnessed that the synthesized profile has much wider line width than those of the individual line profiles,and its line width is close to that of the observed profile.Thus we demonstrate that the correct temperature cannot be derived from the line width in our case.

Figure 12.Non-thermal broadening.The two dotted and one black normalized intensity profiles are produced from three individual sources with formation temperatures but different line-of-sight velocities.The red profile is synthesized from these three sources.An observed profile is depicted as the green curve for comparison.

Figure 13.Two-dimensional reconstructed images of fitting results at the Mg I b2 line in case of EP.

Now let us analyze the spatial distributions of these recovered line parameters.In order to see the distributions of these line parameters more intuitively,we depict these corresponding maps according to the table in Figure13,among which maps ofIcand integratedIlare shown for comparison.It is important to note that on this map we still show the distribution ofIc,not,but they are the same distribution.Before analyzing the maps,it is worth taking into account the code of fiber displayed in Figure13with a period of 5,and the characteristics of the distributions are easily seen to have in mind the scenario that the top rightmost point(P24)is the closest to the solar limb and the bottom leftmost point(P0)is the farthest away from the limb,and the radial direction is indicated by an arrow in this figure above theIcmap.For the continuum intensityIc,the height variation is almost regular in the sense that it decreases totally with height,i.e.,approaching the spherical symmetry,though one outstanding exception can be found at P21 where the intensity becomes smaller than in that case of the approximately spherical symmetry.For distribution of the intensityIlintegrated over the line,the intensity becomes weakest in greatest heights,but it reaches the brightest at P23 rather than the lowest point P24.This is an exception.Again,the intensity distribution of higher points seems closer to the spherical symmetry.The two distribution patterns are similar because both of them are strongly dependent on the particle density,but the difference in the points with lower projective heights is evident in these lower points.We do not depict the map of the ratio of the integrated line intensity to the continuum one,which is very similar to the map of emissivity ratio ζ,as pointed out previously.The distribution patterns of line parameters β,r0,т01will show patterns completely different from those ofIl,orIcor their ratio map close to that of ζ.From map of β,the ratio of the line source function to the continuum one,it is hard to find a clear regularity of variation with the height.The largest value locates at P2 rather than P0,and smallest values are gathered mainly in the upper rows in the map,and two points including the farthest point P0 on the bottom row have also small values.The magnitude of β varies more than one order over the FOV.The distribution of ζ,the ratio of the line emissivity to the continuum one,shows another complex pattern different from that of β.Greatest values indicated by the bright points in the map locate close to the highest point P0,and smallest values spread mainly in the rightmost and leftmost columns.It is noticeable that its variation range is narrow lees than twofold.The map ofr0,the ratio of continuum opacity to line opacity,is not like that of ζ,but much closer to the map of β,with exceptions at some points on the second row (counted from bottom to top).The similarity is understood by the fact that,as can be seen from Equation(10),the two parameters are related via ζ,the latter value is not greatly variable over the FOV.A larger0value suggests that in these layers,the continuum absorption still plays an important role in the places where the spectrum turns to be of emission.

The distribution of the line center optical depth is found to be irregular again from the map of т01,measured off the limb along the line-of-sight rather than along solar radius on the disk.The thickest is at P15,close to the lowest point P20 where the optical depth is smaller.The optically thinnest points are mainly gathered in the highest layers,this agreed with the common knowledge,but some points such as P23 are probed to be also thicker.This suggests that matter of the middle chromosphere is neither uniformly nor symmetrically distributed with height but complicated pattern can be found in the lower layers.The value variation range is narrow from 0.42 to 0.91.On the other hand,these values mean that the optical depth is not small in the middle chromosphere due to the great light path along the line-of-sight and non-ignorable absorption,as witnessed before by the absorption in the far wings of theb2line.It is noticed that in the points with greater heights,this distribution is similar to those ofIc,but at the low height points,no clear correlation with height can be seen.This hints that the radiative transfer becomes complicated there.The line-of-sight velocityvlos,measured from the line center wavelength displacement from that obtained in the quiet Sun region at the disk center,also shows an irregular distribution.They are all less than the average of disk wavelength,that means they are all redshifted.The largest velocity appears at P21,a point with intermediate projective height,and the smallest velocity is observed at the highest point.Once again,the velocity variation is limited twofold in the FOV of 10″ by 10″.Finally,the map of the line width expressed by the FWHM shows a distribution completely different from the other ones,especially the positions of the smallest and largest values are different from the other maps.Although the largest width appears at the point P3 with a large height,a smaller width is found to be at the highest point P0.However,the variation range of these values are very small,or the width in these layers are almost constant.Because we have demonstrated that the proper temperature cannot be correctly derived from the width,it seems that the broadening mechanism in these layers may be complicated.For instance,another mechanism different from causality by the non-Maxwellian velocity distribution is that if the two radiative sources locate in optically thin points along the line-of-sight with close but different line-of-sight velocities and comparable line intensities can cause the apparent line broadening.

From the above views of these maps,it is concluded that the distributions of the two intensities can be approximated by the spherical symmetry,but distributions of all the line parameters revealed by the spectral profile analysis are very complicated,because no spatial symmetry can be fit for them,especially in the lower layers.In fact,the Doppler velocityvlos,as not only a line parameter but also a physical quantity,shows a very complicated distribution pattern with respective to the projective height as an example.This may hint that other physical quantities like the temperature and particle density determining the line profile thus the line parameters may be also irregularly distributed.In other words,the irregularity of the distributions of the line parameters may be caused by the irregular distributions of the physical quantities.

5.Conclusion and Discussion

We present the distributions of the line parameters in the middle solar chromosphere by analyzing the eclipse flash spectrum data of the neutral magnesiumb2line.It is found that the distributions are irregular of the line parameters such as the ratio of the line source function to the continuum one β,the ratio of the line emissivity to the continuum one ζ,the ratio of the continuum opacity to the line oner0,the line center optical depth т01,the macro line-of-sight velocityvlosas well as the line width ΔλD.Among them,maps of β andr0look like each other in most area of the FOV because ζ varies within a narrow range in the FOV.They are very different from maps of the other line parameters.The latter maps differ so greatly that we cannot present any similarity among them.On the other hand,maps of all of these line parameters show non-symmetric characteristics,while the maps of the integrated line intensity and continuum intensity show an approximately spherical symmetry.Since these parameters are extracted from the spectral profiles,we conclude that the features of the profiles are irregularly distributed,as witnessed by Figure10.The physical insight behind it is that some of physical quantities such as temperature or particle density,like the line-of-sight velocityvlos,would be irregularly distributed,or regular distributions of the line parameters are resulted in.

On the other hand,a great change occurs in β,the ratio of the line source function to the continuum one,to an extent of more than one order.This reflects the combined effect concerning the absorption and emission in these atmospheric layers.In fact,the ratio of the line emissivity to the continuum one from the thermal pool,ζ,is almost constant,whiler0,the ratio of the continuum opacity to line one,varies greatly by more than one order.This explains the great variation of β since β=ζ×r0.The macro Doppler velocity is ranged from 8.40 to 13.79 km s-1,indicating that strong flows of matter exists in these domains.By comparison between the results of Li et al.(2016),who analyzed thevlosdistribution in higher FOV,and this paper.It becomes clear that the microline-of-sight velocity increases with the height.

Finally,it is shown that we cannot extract exactly the effective dynamic temperature from the anomalously large Doppler width after calibrating the instrument profile.This is because the spatial coverage extends 1500 km for each pixel of the prototype FASOT,within it there may be multiple individual radiative sources that are indistinguishable,and these sources can have very different line-of-sight velocities.The synthesized profile shows a much broadened configuration.This is one example for non-thermal broadening.

Acknowledgements

This work is sponsored by the National Natural Science Foundation of China (NSFC,Grant Nos.11527804,U1931206,11373065,11078005,10943002 and 12003066).