基于RF-Kmeans-LIBSVM 的乌鲁木齐市颗粒物浓度预测研究

李爱英

（新疆维吾尔自治区环境工程评估中心，新疆 乌鲁木齐 830016）

近年来，空气污染已经成为了公众所热议的话题，尤其是对于发达城市而言，其影响的人群更多更广。中国空气污染状况呈现出冬半年较严重，夏半年较轻，北方地区较严重，南方地区较轻的分布特征[1]。为了遏制空气污染的进一步恶化，相关部门采取了一系列高效的空气污染防治措施并取得了不错的效果[2]，即便如此，仍然不能放缓空气污染防治的脚步，气象部门应不断规范污染预报预警信息的发布，加强气象灾害的防御工作，以便带来不必要的损失。

空气污染带来的危害不仅局限于人体健康方面，其对气候、植物以及生态系统也会产生影响[3−7]。大气污染给人体健康带来的危害是多方面的，主要会造成生理机能障碍和呼吸系统疾病，人体眼睛与鼻子等器官中的粘膜组织受到污染气体的刺激也会引发患病。大气污染物，尤其是二氧化硫、氟化物等对植物的危害也是十分严重的，当污染物浓度很高时，会对植物产生急性危害，使植物叶表面产生伤斑，或者直接使叶片枯萎而脱落；当污染物浓度不高时，会对植物产生慢性危害，尽管表面上危害症状并不明显，但实际上植物的生理机能已受到了侵袭，进而使得产量下降，品质变差。除此之外，大气污染还能对气候产生影响，可以减少到达地面的太阳辐射量，二氧化硫经过氧化会形成硫酸，伴随自然降雨落到地面，破坏建筑物和农作物。

由于空气污染会给居民的生产生活带来不便，因此对于空气质量的准确预报就非常重要。目前国内的学者们在空气污染物浓度预测方面做了诸多尝试，其主要方法有数值预报和统计预报。相比于数值预报，统计预报无需考虑复杂多样的化学物理过程，模型的构建过程比较简单，使用起来也更加方便，尤其是近年来一些机器学习算法在环境和气象预测领域表现优异[8−13]，使得统计预报方法的应用越来越广泛。李龙等[14]利用最小二乘支持向量机对PM2.5浓度做了预测，研究发现引入综合气象指数可以使得预测结果的误差降低约30%，此外还发现了PM2.5浓度与住院率、医院门诊量高度相关；刘杰等[15]构建了包括机器学习算法在内的4 种模型对PM2.5质量浓度进行了预测，通过对比研究，发现支持向量机可以更好地捕捉到PM2.5质量浓度与预报因子之间的非线性关系，整体的预测准确度更高，可作为首选方法；李勇等[16]将小波分析与BP 神经网络相结合对PM10浓度进行了预测，发现结合后的模型比传统的BP 模型预测精度更高；梁泽等[17]利用经遗传算法优化的径向基神经网络模型预测了北京市24 小时的平均PM2.5浓度值，结果发现该模型预测性能良好且无需输入地理位置信息与气象等数据，依赖变量少且预测准确率高（R2高达75%），能够对多种时空情境下的城市空气污染物浓度进行预测；为了提高多变天气情况下PM2.5浓度的预测准确率，李芬等[18]对天气类型进行聚类与识别，基于LSTM 算法构建了不同天气类型下的PM2.5浓度预测模型，研究发现该方法比传统BP 神经网络与支持向量机方法效果更好。本文利用空气质量监测数据（包括SO2、NO2、O3、CO、PM10和PM2.5）与气象数据，基于RF-Kmeans-LIBSVM算法建立PM2.5与PM10日均浓度的预报模型，为相关部门制定决策提供理论依据。

1 资料与方法

1.1 数据来源

空气污染物浓度监测数据来源于环境监测站，气象数据来自天气后报网站（http://www.tianqihoubao.com/），选取乌鲁木齐市的逐日数据，时间段为北京时间2015 年1 月1 日～2020 年12 月31 日，空气污染物浓度监测数据包括的要素为：SO2、NO2、O3、CO、PM10和PM2.5这6 种污染物的日均浓度值；气象数据包括的要素为：风向和风速、天气状况、最高和最低气温。首先对数据进行质量控制，将序列中乱码和缺失的数据进行识别与剔除，采用相邻非缺失值线性插值的方法进行订正。为了消除不同量纲单位之间的差异，在建立模型之前需要使用公式（1）将所选数据归一化到指定区间（0，1）内。

式中，Xn代表经归一化处理之后的数据，X代表经归一化处理之前的数据，Xmax代表样本数据中的最大值，Xmin代表样本数据中的最小值。

1.2 研究方法

1.2.1 RF 重要性评估 随机森林算法（RF）[19−22]是由LEO Breiman 教授提出的，该算法能够对特征变量的重要性进行评估，在非线性问题中表现优异，付旭东[23]使用RF 重要性评估的方法结合机器学习预测模型有效提高了风场预报的准确率。使用RF 算法筛选出重要变量的思想是看每个特征对随机森林中每棵决策树的贡献程度，然后取该特征贡献的平均值，最后依据贡献值大小对每个特征进行排序。通常情况下，可以通过基尼系数对各个因子的贡献大小进行衡量。

1.2.2 K-Means 聚类分析 K-Means 算法[24]作为应用最为广泛的聚类分析算法之一，是一种非常典型的基于距离的硬聚类算法，认为对象之间的距离

越小，相似性就越大。K-Means 聚类是基于样本集合划分的聚类算法，它将样本集合划分为K个子集，构成K个类，将n个样本分到K个类中，每个样本到其所属类的中心距离最小，每个样本仅属于一个类。K-Means 聚类算法的实现过程，见图1。

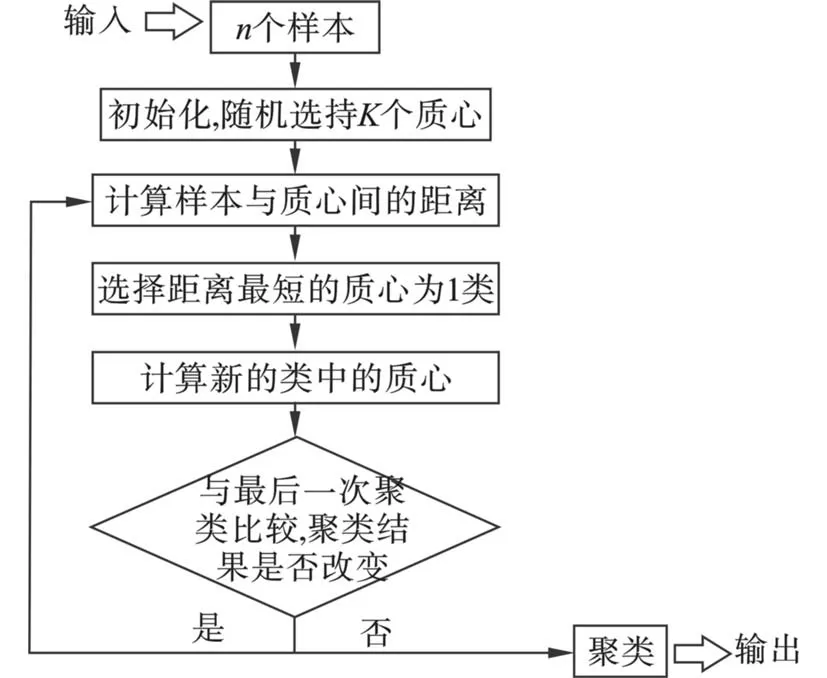
图1 K-Means 聚类算法的实现流程

1.2.3 LIBSVM 回归预测 LIBSVM 是由林智仁副教授设计发明的，如今已经被广泛应用于回归拟合问题[25−26]。传统支持向量机预测模型有一个明显的缺点，就是只能依靠经验和对比实验来进行选取核函数以及其他参数，而LIBSVM 的出现则克服了这一缺陷。相对于传统支持向量机（SVM）模型，LIBSVM 的很多参数都是默认的，涉及到的参数调节更少，合理利用这些设置好的默认参数可用来解决许多问题，LIBSVM 还在传统SVM 的基础上提供了一种用于交互检验的新功能。

1.2.4 误差评价指标 选用平均绝对误差（MAE）、均方根误差（RMSE）和预报准确率（P）3 个误差评价指标对PM2.5和PM10浓度的预测结果进行检验，每种误差评价指标的计算过程，见式（2～4）：

2 实例分析

2.1 基于RF 的预报因子重要性评估

本文在构建PM2.5和PM10浓度预报模型时，除了考虑前日的6 种污染物浓度值和AQI 指数对次日PM2.5和PM10浓度的影响外，还考虑了预测日的最高气温、最低气温、风速、风向和天气状况等。为了减小浓度的突然波动对预测结果的影响，这里采用滑动平均法对污染物浓度进行3 d 滑动平均处理。将预测日的天气状况进行分类，分为晴、阴、多云、雾、雨、雪和雨夹雪等7 种天气类型，并将以上7 种天气类型分别用数字1～7 表示；风向用角度值表示。颗粒物浓度预报中预报因子的变量符号及其物理意义，见表1。其中，X表示输入变量，Y表示输出变量。

表1 颗粒物物浓度预测中预报因子的变量符号及其物理意义

颗粒物浓度预测中影响PM2.5和PM10浓度的因子重要性评分，见图2。

图2 乌鲁木齐市颗粒物预报中各预报因子的重要性评分

对于PM2.5而言，排名在前3 位的预报因子依次为前日的PM2.5浓度、前日的CO 浓度和预测日的天气状况；对于PM10而言，排名在前3 位的预报因子依次为前日的PM10浓度、预测日的天气状况和前日的O3浓度。总的来说，当以某种颗粒物浓度作为输出变量时，前日的该颗粒物浓度对预报结果的贡献最大，预测日的天气状况也是一个不容忽视的预报因子。

2.2 基于K-Means 的颗粒物浓度聚类

对于PM2.5而言，选择重要性评分最高的2 个因子进行聚类运算，它们分别为前日的PM2.5浓度和前日的CO 浓度；对于PM10而言，重要性评分最高的因子为前日的PM10浓度，预测日的天气状况与前日的O3浓度紧随其后且两者的评分大小相差不大，考虑到天气状况的数据是通过定性分析转化而来的，数据精度不高，因此选择前日的PM10浓度和前日的O3浓度进行聚类运算。经试验发现，当K值＜2 或＞7 时，PM2.5模型的训练误差会明显增大，当K值＜3 或＞8 时，PM10模型的训练误差会明显增大，因此，从2～8 依次设置K值，利用SPSS软件进行聚类分析，可得到不同K值下的聚类数据与质心，经过多次统计尝试发现当PM2.5和PM10都被分为4 个类别时预测效果最好。K=4 时颗粒物的数据样本聚类结果，将PM2.5和PM10各自分为4 个类别，针对每个类别的数据分别建立模型，见图3。

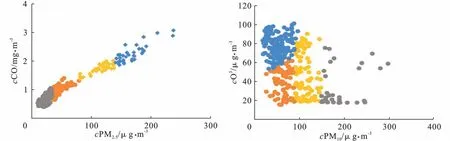
图3 数据样本聚类结果

经聚类分析后基本能够将不同浓度范围的颗粒物浓度值分开，分为4 类，然后针对每一类分别构建预报模型，减少数据的样本差异给预报结果带来的干扰，降低模型的过拟合程度，提高预测精度，见表2。

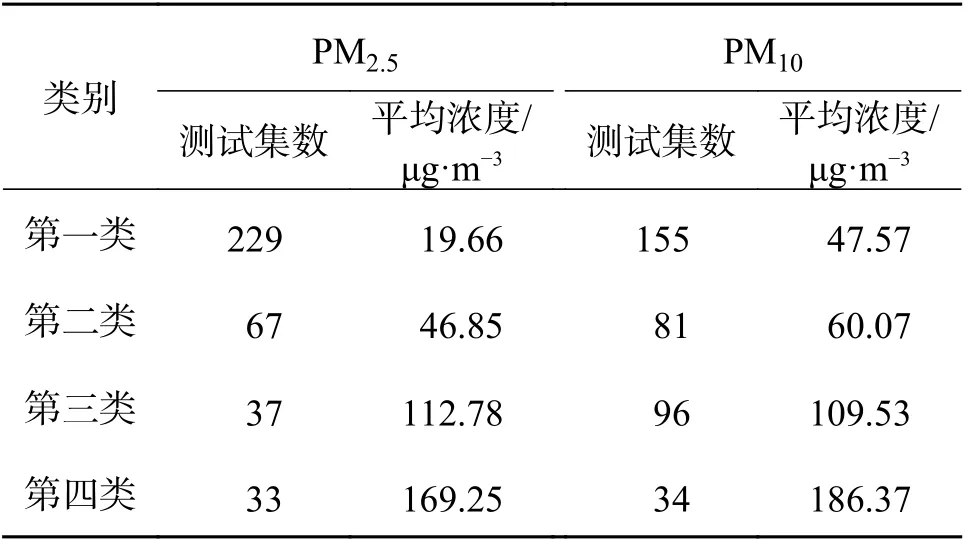
表2 聚类结果

2.3 预测模型的构建与检验

利用LIBSVM 的回归原理构建大气颗粒物浓度预报模型。将数据集划分为训练数据和测试数据，其中训练数据和测试数据又各自包含输入数据与输出数据。选取2015 年1 月1 日～2019 年12 月31 的数据作为训练数据，2020 年1 月1 日～2020 年12 月31 日的数据作为测试数据，以此来构建基于LIBSVM 的颗粒物浓度预报模型。

（1）调入数据，对数据进行归一化处理。

（2）利用RF-Kmeans 算法对颗粒物数据进行聚类运算，将PM2.5和PM10分别分成4 种不同类别。

（3）采用LIBSVM 算法对各个类别的模型分别进行训练。

（4）将测试数据中的输入数据输入到已经训练好的预报模型中，输出经模型预报的颗粒物浓度数据。

（5）反归一化，得到空气颗粒物浓度预报值的最终结果。

（6）对模型输出的空气颗粒物浓度预报结果进行误差分析，评价模型的泛化能力。

根据以上建模步骤，给出了不同颗粒物浓度序列的RF-Kmeans-LIBSVM 预测结果，见图4 和5。

图4 不同类别PM2.5 浓度序列的预测结果

图5 不同类别PM10 浓度序列的预测结果

总体上，颗粒物的预测值能够较好地反映出真实值的变化趋势。从预测值与真实值之间的相关程度来看，无论是PM2.5还是PM10，相关系数都在0.54 以上：对于PM2.5来说，第一类为0.83，第二类为0.69，第三类为0.54，第四类为0.73；对于PM10来说，第一类为0.81，第二类为0.67，第三类为0.55，第四类为0.66；这说明预测值与真实值之间有较高的正相关关系。

为了验证该模型的泛化能力，本文采用未经聚类分析的传统LIBSVM 模型对颗粒物浓度进行预测，为了更加直观地对比模型优化前后的整体预测效果，首先将聚类分析后得到的颗粒物预测数据按照时间的先后顺序进行整合,得到整体的颗粒物浓度序列预测结果，再对实际监测值和预测值之间进行相关性分析。若实际监测值与预测值之间相差较小，则在相关性分析图中呈现为收敛，即相关性较好，反之则呈现为发散，相关性较差。各图中的折线图表示PM2.5和PM10实际即监测值与预测值的对比效果图，散点图表示实际监测值与预测值之间的相关性分析图，预测结果见，图6～9。

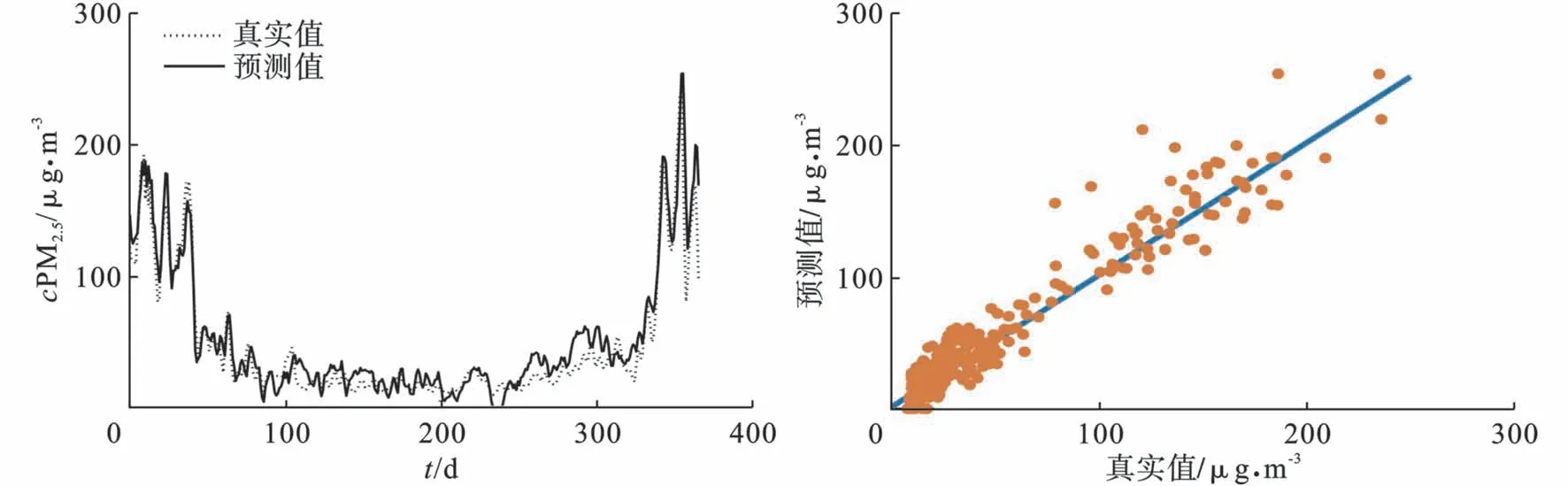
图6 LIBSVM 模型的PM2.5 浓度预测结果

图7 RF-KMeans-LIBSVM 模型的PM2.5 浓度预测结果

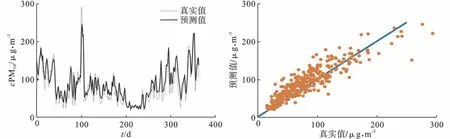
图8 LIBSVM 模型的PM10 浓度预测结果

图9 RF-KMeans-LIBSVM 模型的PM10 浓度预测结果

图中可以看出，颗粒物的预测值能够较好地反映真实值的大小及变化趋势，预测值与真实值之间的相关程度较高，对PM2.5而言，LIBSVM 模型的相关系数为0.961，RF-Kmeans-LIBSVM 模型的相关系数为0.975；对PM10而言，LIBSVM 模型的相关系数为0.906，RF-Kmeans-LIBSVM 模型的相关系数为0.919。

相对于传统的LIBSVM 预测方法，经聚类分析优化之后的RF-Kmeans-LIBSVM 预测方法的各项误差评价指标得到明显提升，说明RF-Kmeans 聚类方法能够为模型提供相似度较高的训练样本，从而提高训练效率，进而使得模型的泛化能力得到显著提高，见表3。

表3 不同模型预测性能的比较

从预测整体效果方面看，本方法通过聚类分析对模型实现了优化，在对PM2.5的预测中，MAE、RMSE 分别下降了33.1%和26.5%，准确率提高了7.4%；在对PM10的预测中，MAE、RMSE 分别下降了15.7%和12.7%，准确率提高了3.3%，表明了该方法能够大幅度地提高LIBSVM 模型对大气颗粒物浓度的预测性能，具有一定的实用价值，可为颗粒物质量浓度的预测业务提供参考。

3 结论

本研究基于乌鲁木齐市2015～2020 年的空气污染资料与气象资料，利用RF-Kmeans 的聚类方法对空气颗粒物数据进行分型，结合支持向量机回归模型对PM2.5和PM10质量浓度分别进行了预报，主要结论如下。

一是在所选预报因子中，前日的PM2.5浓度对预测日PM2.5浓度预测的贡献最大，其次是前日的CO 浓度和预测日的天气状况，前日的PM10浓度对预测日PM10浓度预测的贡献最大，其次是预测日的天气状况和前日的O3浓度。

二是使用RF-Kmeans 聚类方法将颗粒物浓度数据分成相似度较高的若干类，针对每一类分别构建预测模型，并用各类颗粒物浓度数据训练各类模型，不仅可以提高模型的训练速度， 还可以提高模型对此类数据的泛化能力，提高模型的预测准确率。

三是相对于传统支持向量机预测模型，该预测方法对PM2.5预测结果的MAE、RMSE 分别下降了33.1%和26.5%，对PM10预测结果的MAE、RMSE分别下降了15.7% 和12.7%。可将该方法推广至乌鲁木齐市空气质量预报业务中，为空气质量业务化预报提供技术支撑。