自抗扰控制器在球杆系统中的应用与研究
翟光雯,陈海峰
(1.芜湖市科技馆,安徽 芜湖 241000;2.安徽工程大学,安徽 芜湖 241000)
球杆控制系统的非线性研究具有重大的意义,其结构简单,工作原理直观。因本身的非线性问题,在电位计对小球位置测量时,由于电压波动导致的不连续性等非线性因素,且球杆控制系统易受到多方干扰。因此,对实际非线性稳定性的研究可以移植到球杆系统上来[1-3]。
国内外学者对球杆系统进行了大量研究。李真等[4-8]对球杆系统采用了自适应控制策略,提高了控制性能如对外部干扰的抑制,但是文章并没有提到内部干扰对系统的影响;曹海青等[9]利用自适应网络控制和分数阶PID 控制相结合,针对球杆系统的数学模型不确定性问题进行了研究仿真,设计过程简单,并取得了较好的控制效果;作为经典的控制策略,PID 控制器在球杆系统中得到了一定的应用[10-13]。球杆系统的不稳定特性对整个球杆系统有较大的影响,PID 控制不能较好地对其进行控制。
球杆系统的研究不仅有以上所陈述的控制,还有模糊控制、有限时间控制、滑膜控制、分数阶控制等策略[14-17],有效提高了球杆系统的控制效果。由于球杆系统的外部、驱动机构和执行机构带来的干扰未能得到很好地抑制,该系统的控制精度已经不能满足人们的需求。为此,本文设计了一种自抗扰控制策略,不仅有效跟踪了小球的位置还抑制了系统的总扰动,很好地控制了小球的运动,提高了系统的稳定性和控制品质。
自抗扰控制器是韩京清先生提出的,采用了能提供更好的噪声衰减性能并避免抖振现象的跟踪微分器。为了提高快速运动条件下的伺服平台跟踪性能,提出了一种新型的NLSEF;哈尔滨工程大学研究员将自抗扰控制技术应用到水下机器人,仿真得出其具有自适应性和鲁棒性[18]。周凯等[19]在滑膜控制的基础上,为解决永磁同步电机的速度不可控问题设计使用了自抗扰控制技术,实现了4 段式速度伺服控制。然而在解决此问题的过程中,出现了大量的参数需要整定。为了解决此问题,刘丙友等[20]运用等效替代法对PIDNN 的参数整定进行了公式推导从而整定出自抗扰控制器的参数,代替了经验法的参数整定;王丽君等[21]在其他学者的研究基础上提出了基于粒子群算法的自抗扰控制器运用于航天器姿态控制,通过该方法优化了参数,使参数选择不再依赖于经验。因此本文将使用自抗扰控制器对球杆系统进行研究。
本文首先建立了球杆系统的数学模型,然后对自抗扰控制进行概述,随后通过自抗扰控制器对球杆系统的不精确数学模型、球杆系统内部及外部的干扰等进行及时补偿,扩张为一个新的状态变量,最后基于自抗扰控制器对球杆系统进行仿真。
1 球杆系统的数学模型
球杆系统的支撑导轨是由测量小球位置的刻度尺和将位置信号转换为电压信号的电位计两部分构成。球杆系统的整体结构图如图1 所示。系统通过改变直流伺服电机的位置角最终确定横杆的角度,使小球在重力的作用下在支撑导轨上运动。
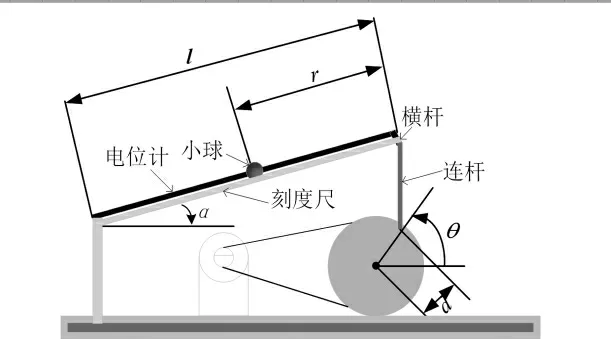
图1 球杆系统的整体结构图
设小球的质量为m,坐标位置为(x,y),根据直角坐标与极坐标的关系并求导,得到速度关系为:

为此可得小球在轨道上运动W1的动能(即小球沿横杆方向上运动的动能)
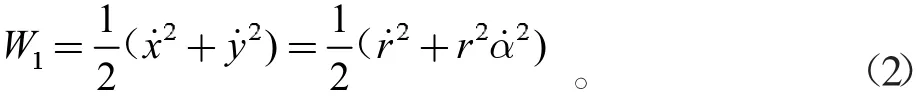
设R为小球的半径,则求导得

则小球沿自身转动的动能W2为

式中:J为小球的转动惯量
小球沿固定端点转动的动能W3为

式中:JL为横杆的转动惯量
故,系统的动能W为

小球沿r方向运动引起的势能为

球杆自身旋转所引起的势能为

总势能V为

根据Lagrange 函数对T定义:系统总动能W与系统总势能V之差,即T=W-V得:

根据Lagrange 运动学方程式(1)得

由上式得
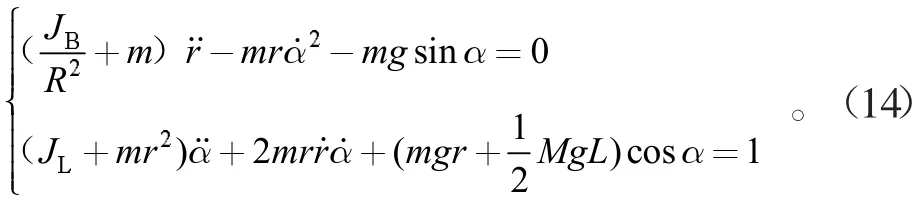
对球杆系统简化处理得

当齿轮转动时就会导致连杆上下移动,连杆作用到导轨上使得其绕固定端连杆的顶端上下转动。转角θ 和转角α 之间的关系可以由式(16)表示:
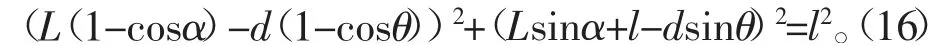
从式(16)中我们发现该方程是一个非线性函数,因此简化处理可得

将式(17)带入到式(15)得

将上式变换得
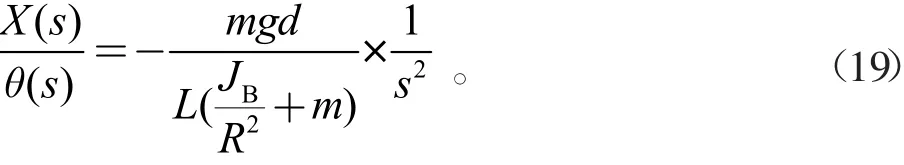
2 自抗扰控制器的设计
2.1 跟踪微分器
跟踪微分器为球杆控制系统提供一个优质的信号,对球杆系统输入安排过渡过程[22]。
球杆控制系统跟踪微分器为

式中:r为球杆控制系统的输入信号;x1是球杆系统的跟踪;x2是球杆系统跟踪信号的微分;fhan(ψ,x2,r0,h0)为最速控制综合函数,

2.2 扩张状态观测器
扩张状态观测器对球杆系统的各种不确定性进行补偿。本文所设计的改进型自抗扰控制器中采用了2个ESO,ESO1 用来观测估计小球的位置信号和系统外环的扰动,ESO2 用来驱动机构的位置角和系统内环的扰动。改进型ESO 表达式:
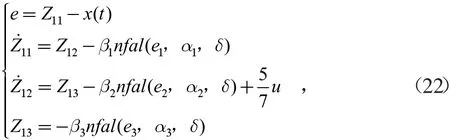
式中:e1,e2,e3分别为球杆系统的误差,误差的积分,误差的微分;x(t)为球杆控制系统小球的输入位置;Z11是小球的跟踪信号;Z12是小球跟踪信号的微分信号;Z13是球杆控制系统的总扰动;α1,α2,α3为非线性因子;β1,β2,β3是ESO 的增益。
2.3 非线性状态误差反馈控制律
NLSEF 表示跟踪差分(TD)的输出与扩展状态观测器(ESO)产生的状态变量估计之间的非线性连接。
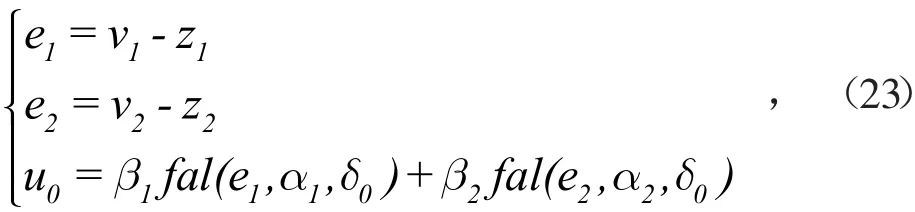
式中:α1,α2,α3为函数的非线性因子;β1,β2为函数的增
益。它具有良好的适应性和鲁棒性。
2.4 系统的整体结构
系统总体结构如图2 所示。

图2 球杆系统的自抗扰控制策略
改进型NLSEF 是通过非线性组合的方式,它的参数直接对TD 和改进ESO 能否达到最佳组合产生影响。改进型ADRC 各部分参数见表1。

表1 球杆系统的自抗扰控制策略
3 仿真分析
为了验证本文提出的自抗扰控制策略的优越性,对其进行仿真。输入1 个阶跃函数时,对比图3 中3 种控制器的响应曲线,其中小球到达指定位置时PID 最慢,改进的ADRC 速度最快,且小球达到稳定时间最快,传统ADRC 介于2 者之间。改进型ADRC 解决了超调和快速响应之间的矛盾。

图3 阶跃响应曲线
输入一个正弦函数时,观察图4 中3 种控制器都有较好的跟踪效果。从图中能发现,PID 控制的超调量较大,传统ADRC 和改进型ADRC 都无超调量,但在跟踪效果上,改进型ADRC明显比传统ADRC的效果要好。
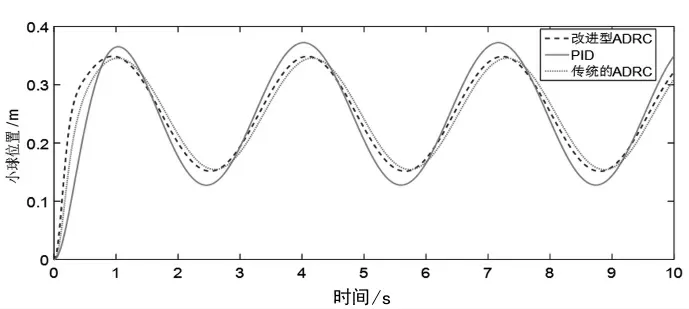
图4 正弦响应曲线
为了更好地验证改进型ADRC 控制器的鲁棒性,对不同方差的白噪声干扰进行仿真。从图5 中发现PID 控制器的输出幅值有明显的波动,传统ADRC 有较小的波动,改进型ADRC 基本无波动。从而验证了改进型ADRC 的鲁棒性较强。


图5 白噪声干扰响应曲线
4 结论
从仿真实验可知,在球杆系统中,改进型ADRC 控制器具有更好的控制效果。相比于两种传统的控制策略,改进型ADRC 控制器响应速度更快,抗干扰能力更强,具有更好的鲁棒性,具有一定的工程意义。

