基于随机抽样一致算法的水深反演技术研究
白 龙,黄文骞,程益锋,朱立波
(1.海军大连舰艇学院,辽宁 大连 116018;2.91351 部队,辽宁 兴城 125106)
掌握岛礁附近海域水深信息对船只安全航行有重要意义。传统的船载单波束、多波束测深技术发展成熟,测深精度高,得到了广泛应用。20 世纪60 年代以来,遥感卫星和计算机技术飞速发展,被动遥感水深反演具有成本低、探测范围不受限制等特点,在船只难以到达的岛礁附近海域的水深探测中发挥着无可替代的作用。
目前被动遥感水深反演模型发展已经成熟,分为理论解析模型、半理论半经验模型和统计模型。半理论半经验模型中的单波段对数线性模型是理论解析模型的简化,只需要较少的回归系数就能得到精度较高的水深反演模型[1]。Paredes 等[2]建立的多波段对数线性模型能够降低海底底质的影响,提高反演精度。Stumpf[3]提出的波段对数比值模型能够降低水中杂质的影响,反演稳定性明显提升。党福星等[4-6]通过底质分类和水深分段等方法进一步提升水深反演精度。大量学者研究表明,将机器学习应用在水深反演领域,其性能在一定程度上优于传统水深反演模型[7-10]。李丽[11]将赵述岛的水深反演模型应用到南岛,反演误差在1.25 m 以内。赵露露等[12]研究了将水深反演模型推广至无实测数据海域的可行性,结果表明海底地质相同或相近的海域,水深反演模型的推广性更高。利用在巡航船只上安装单波束或多波束测深仪,以巡航作业的方式,能够采集争议岛礁附近海域的少量实测水深数据。由于船只在巡航时获取的实测水深数据较少,难以构建较准确的水深反演模型。
为了提升争议岛礁附近海域的水深反演精度,本文对随机抽样一致算法进行改进。首先利用同一海域其他岛礁已有的实测水深数据建立水深反演模型,将得到的模型回归系数作为随机抽样一致算法的初始输入系数,通过迭代获取足够多的局内点后重新建立争议岛礁附近海域的水深反演模型,并对比了基于波段对数比值模型的4 种反演争议岛礁附近海域水深的方法。
1 实验原理
1.1 最小二乘法
最小二乘法是通过已知的m个观测数据(xi,yi)(i=1,2,3,…,m),构建如下残差函数,找到一组ωi(i=1,2,3…m),使残差函数L取得最小值的曲线拟合方法。
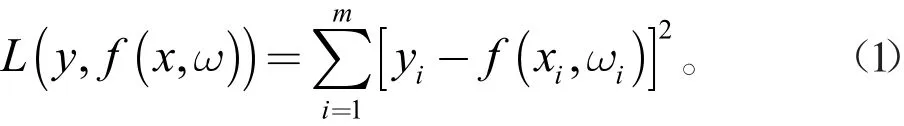
在水深反演实验中,通常采用最小二乘法建立遥感水深反演模型,并根据此模型反演水深。但是需要反演水深的海域是非建模区域,其反演精度与建模区域相比较低。为了提高水深反演精度,将安装单波束或多波束测深仪的船只在争议岛礁附近海域巡航时采集的少量实测水深数据与遥感影像数据匹配,得到水深反演观测数据,再利用观测数据构建水深反演模型。
利用最小二乘法建立水深反演模型时的数据越多,所建立的模型精度越高,但是船只巡航采集的实测数据较少,抵抗粗差能力差,难以建立精度较高的水深反演模型。为了降低反演误差,增加水深反演可靠性,需要筛选观测数据,建立精度更高的水深反演模型。
1.2 改进的随机抽样一致算法
随机抽样一致算法是采用迭代的方式从一组含有局外点的数据中估计出数学模型参数的方法。与最小二乘法不同的是,随机抽样一致算法不是利用所有观测数据拟合曲线,而是通过迭代,筛选出可靠性较高的观测数据估计出最优模型。其一般步骤如下。
(1)假设有一个观测数据子集,是参数化数学模型L1的局内点,即该数学模型参数能够通过这些局内点拟合得到,随机选取子集中的N个点来构建数学模型L2,N为模型未知参数个数。
(2)设置一个阈值D,判断观测数据与数学模型L2的距离,小于D 的点是适用于模型的局内点,大于D 的点是不适用于模型的局外点。
(3)重复上述2 个步骤,直到获取的局内点满足要求,就认为此时建立的模型是最优模型。
随机抽样一致算法鲁棒性好,即使存在较多局外点也能估计出较准确的模型,适用于利用少量观测数据建立水深反演模型。本文根据水深反演的特点对随机抽样一致算法进行改进。经过遥感影像预处理,有实测数据的岛礁附近海域A 和争议岛礁附近海域B 受大气环境和水体环境影响较小,在海底底质相同或相似的情况下,海域A 与海域B 的水深反演模型回归系数相近,把海域A的水深反演模型的回归系数作为随机抽样一致算法的初始输入系数,再结合船只在海域B 获取的巡航数据进一步优化模型。改进算法步骤如下。
(1)建立海域A 的波段对数比值模型,如公式(2)所示,其中z为水深值,m1,m0,n为回归系数,L(λ)为波段λ的遥感反射率,将海域A 的回归系数m1、m0设为随机抽样一致算法的初始输入系数。
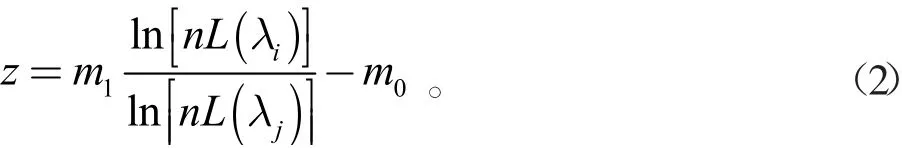
(2)设置阈值D,判断观测数据是否适用于式(1)中的模型,适用于该模型的为局内点,反之为局外点。
(3)随机选取局内点中的N个数据重新建立波段对数比值模型,得到模型回归系数。
(4)重复上述步骤,直到局内点数满足要求,所得到
模型为海域B 的最优水深反演模型。
2 实验与分析
2.1 遥感影像数据预处理
本此实验选取我国浪花礁附近海域为海域A,假定我国甘泉岛附近海域为海域B,并模拟船只在海域B 内的一条巡航轨迹上航行,如图1 所示。分别对2 个岛礁的Sentinel-2 遥感影像数据进行水陆分离、太阳耀斑校正[13]和大气校正[14]后提取像元光谱信息。通过关联海域A 和海域B 的实测水深数据与对应位置的像元光谱信息,实现遥感影像数据与实测水深数据的匹配,得到海域A 的建模数据和海域B 的观测数据。
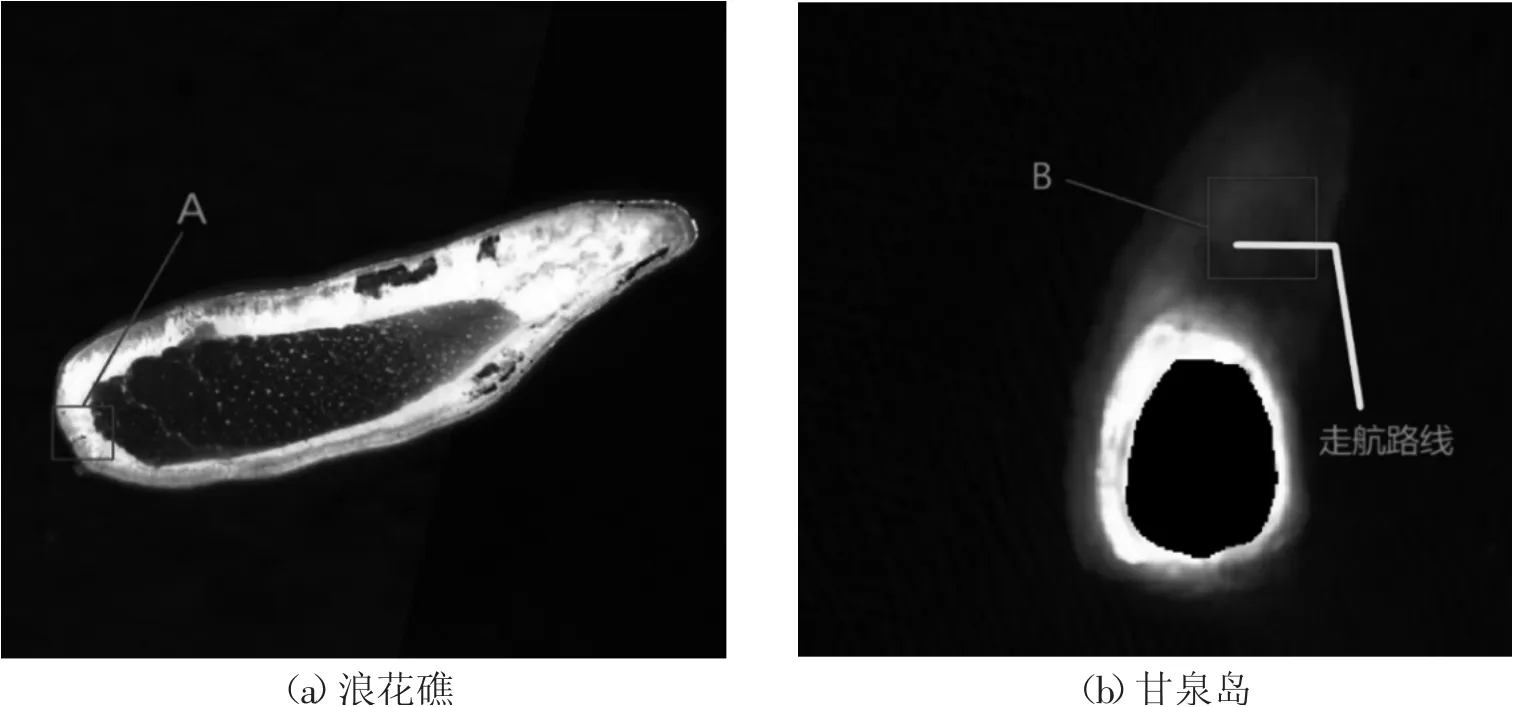
图1 水深反演实验区域
2.2 水深反演实验精度分析
在海域A 建立波段对数比值水深反演模型,将模型回归系数设为随机抽样一致算法的初始输入系数,随机选取的子集个数为模型的未知参数个数,阈值D设为1,算法的迭代次数上限K 设为1 000。按照上述改进的随机抽样一致算法对海域B 的观测数据进行筛选,直到选取的局内点数满足要求,即得到海域B 的最优水深反演模型。
建立平面直角坐标系,纵轴为船只在海域B 巡航获取的实测水深数据,横轴为蓝绿波段对数比值根据公式(2)和z是线性关系。直线a 为利用最小二乘法拟合得到的和z的线性关系,直线b 为用随机抽样一致算法筛选后的数据拟合得到的和
z的线性关系,如图2 所示。
由图2 可和,水深大于15 m 的观测数据存在较多不符合线性关系的局外点。利用最小二乘法拟合得到的模型会受到局外点的影响,而利用改进的随机抽样一致算法筛选后的数据拟合得到的模型能够降低局外点的影响,建立精度较高的水深反演模型。
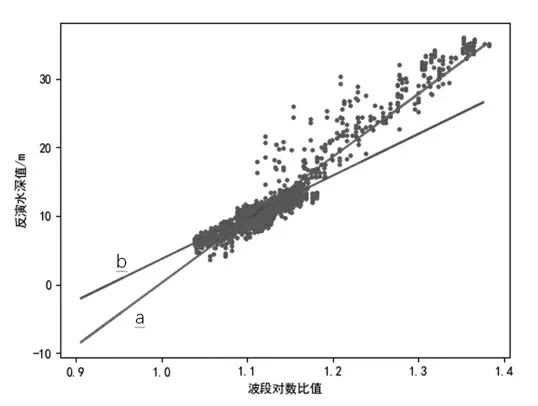
图2 2 种拟合方法效果图
为了体现改进的随机抽样一致算法的适用性,对以下4 种反演海域B 水深的方法进行对比:利用在海域A 建立的模型反演海域B 的水深(方法一),利用海域B 的观测数据建立的模型反演海域B 的水深(方法二),利用改进的随机抽样一致算法建立的模型反演海域B 的水深(方法三),利用海域B 的实测水深数据建立的模型反演海域B 的水深(方法四)。方法四是在建模区进行水深反演,精度最高,因此以方法四作为参照标准。
本文精度评价采用平均绝对误差(MAE)和均方根误差(RMSE)来评定,结果见表1。为了直观观察模型反演效果及偏差,以实测水深值为平面直角坐标系横轴,反演水深值为平面直角坐标系纵轴,得到反演水深与实测水深的偏离情况,如图3 所示。
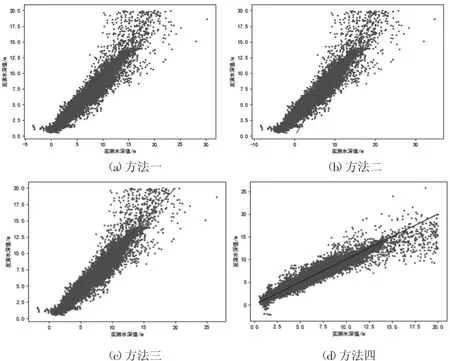
图3 4 种水深反演方法偏离情况图
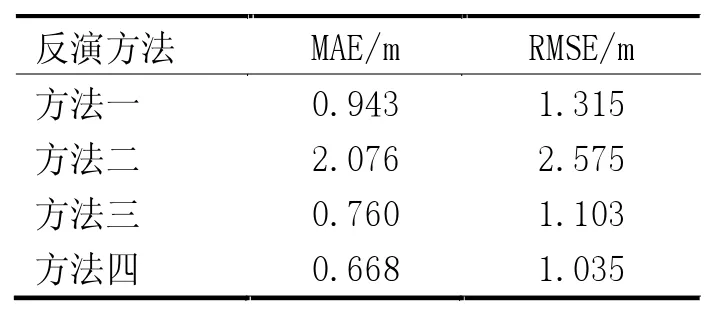
表1 4 种水深反演方法精度对比
从反演数据与实测数据的偏差来看,利用最小二乘法对甘泉岛巡航数据拟合得到的模型反演甘泉岛附近海域水深和利用浪花礁附近海域的模型反演甘泉岛附近海域水深精度较低,与实测数据的偏差较大,而改进的随机抽样一致算法能够降低局外点的影响,利用局内点建立精度较高的水深反演模型,反演甘泉岛附近海域水深的精度更高,与实测数据偏差更小,更接近利用甘泉岛附近海域实测数据建立模型的反演精度。
3 结论
本文首先建立已有实测水深海域的水深反演模型,将得到的模型参数作为随机抽样一致算法的初始参数,通过迭代获取足够多的局内点后建立争议岛礁附近海域的水深反演模型,并对比了基于波段对数比值模型的4种反演争议岛礁附近海域水深的方法,结果表明,利用改进的随机抽样一致算法优化波段对数比值模型,对巡航船只在争议岛礁附近海域巡航时测得的少量实测水深数据进行筛选,能够降低观测数据局外点对水深反演的影响。利用观测数据局内点建立精度较高的水深反演模型,反演效果优于直接利用最小二乘法对争议岛礁附近海域的少量巡航数据建立的模型反演其海域水深和利用已有实测水深的海域建立模型反演争议岛礁附近海域水深的精度。该方法对船只在争议岛礁附近海域的安全航行有积极作用。

