基于BRISK 和改进RANSAC 算法的图像拼接
杜 港,侯凌燕,佟 强,杨大利
(北京信息科技大学 计算机学院,北京 100101)
1 引 言
图像拼接是图像处理的一个重要领域,指的是将两张或多张有重叠像素的图像经过一系列操作组成一张广角图像[1],目前广泛应用于遥感影像配准、计算机视觉、医学图像处理、视觉SLAM 以及嵌入式设备等领域,如相机在拍摄时由于拍摄空间和相机视角局限性的影响,导致单张图像获取信息有限,需要利用图像拼接的方式获得包含信息更加丰富图像。图像拼接主要分为基于频域的拼接方法和基于时域的拼接方法两类。基于频域的拼接方法是通过傅里叶变换将图像变换至频域,然后根据图像间的互功率谱求解出平移矢量,最后根据平移矢量实现图像拼接[2]。基于时域的拼接方法又分为基于灰度拼接和基于图像特征点拼接两类方法,基于灰度的理论研究较早但实际应用相对较少,主要是通过验证图像的灰度相关性来实现图像拼接,该方法在解决图像畸变大、不连续等问题时存在困难,因此,基于灰度的拼接方法难以获得较好的拼接结果[3];基于图像特征点的拼接方法主要通过计算图像特征点的位置关系求解出图像的变换关系,再根据变换关系实现图像拼接,该方法具有计算速度快、鲁棒性强的优势,可以获得较好的拼接结果[4]。目前,图像拼接主要是基于特征点拼接实现的。
常用的特征点提取方法有SIFT(Scale In⁃variant Feature Transform)[5-6]、SURF(Speeded Up Robust Features)[7-8]以 及ORB(Oriented FAST and Rotated BRIEF)[9-10]等方法。SIFT 算法是由Lowe 等人提出的,文献[11-12]将该方法结合RANSAC[13]算法应用在图像拼接中,该算法对尺度缩放、旋转、亮度变化保持不变性,对仿射变换、视角变化、噪声也保持一定程度的稳定性,但是因为使用多次的高斯卷积,使得其存在运算量较大,运行时间较长的缺点,尤其是在算力有限的嵌入式设备上很难满足实时性。SURF 算法是由Bay 等人提出的,文献[3,14]将该方法分别结 合PROSAC[15]算 法 和RANSAC 算 法 应 用 在图像拼接中。SURF 算法是SIFT 算法的一种改进,它使用盒状滤波器代替高斯卷积,再配合上积分图像,大幅减小了特征点的提取时间,但其检测到的特征点比SIFT 算法要多,因此其进行特征点匹配时相对耗时,依然存在运行时间较长的缺点,同样无法较好地在算力有限的嵌入式设备上满足实时性。ORB 算法是由Rublee 等人提出的,文献[4]将该方法结合RANSAC 算法应用在图像拼接中。该算法是一种较为简单的利用二进制特征描述符进行特征点提取的算法,其显著特点是速度超快,具有旋转不变性,在一定程度上不受噪声和图像变换的影响,虽然在算力较低的嵌入式设备上满足实时性,但存在不具备尺度不变性且特征点匹配准确率较低的问题。
为了解决这些问题,本文提出了一种基于BRISK 和改进RANSAC 算法的方法来实现图像拼接。首先,针对特征点的检测速度问题,本文使 用BRISK(Binary Robust Invariant Scalable Keypoints)[16]算 法 进 行 特 征 点 检 测。然 后,为 了在特征点精匹配中得到更多的特征点匹配对数,本文提出了一种基于RANSAC 算法的改进算法:(1)先随机地从粗匹配点对中选择4 个点对计算单应性矩阵H,再根据单应性矩阵H计算统计出内点数,再根据内点拟合出新的单应性矩阵,以此循环,直至内点的个数不再增加为循环的结束,将此操作执行多次,内点数最大所对应的单应性矩阵为最终结果;(2)对RANSAC 的内点将欧氏距离判断改成面积判断。实验结果证明,本文提出的方法可以缩短特征点检测的运行时间且得到更多的内点数,从而提高准确度。
2 实验原理
图像拼接的原理为找到两幅图像中相对应的位置,然后经过对待拼接图像的投影变换,将两幅图像置于同一图像坐标系中,从而完成图像拼接。本文中寻找对应位置使用到BRISK 算法;投影变换关系需使用单应性矩阵表示。
2.1 特征检测算法BRISK
BRISK 算法是由Stefan 等人提出的,该方法和SURF 算法、SIFT 算法一样,具有尺度不变性和旋转不变性,但运行速度优于SURF 算法、SIFT 算法。该方法在运行速度上的优势,主要归结于采用基于FAST 方法进行特征点检测和使用类似于BRIEF 方法的二值位字符串描述符。
BRISK 方法构建了由n个组层和n个组间层组成的尺度空间金字塔(n值一般为4),这样保证了BRISK 方法的尺度不变性。若用t表示图像的尺度,则各层的尺度公式可由式(1)表示:

BRISK 方 法 先 使 用FAST9-16[17]方 法 和FAST5-8[18]方法进行特征点提取,然后对特征点的得分值在相邻的两个尺度空间上进行非极大值抑制,其中得分值为角点响应值。最后,再使用最小二乘法结合得分值拟合得到特征点的亚像素坐标以及对应的尺度。
BRISK 方法的特征点描述符创建是以特征点为中心,围绕特征点有4 个同心圆,每个同心圆的圆周上分布着数量不同的采样像素,从内而外分别为10,14,15,20,加上特征点一共是60 个采样点,将这60 个采样点两两进行组合,可得到1 770 个组合。所对应的数学表示形式见式(2):
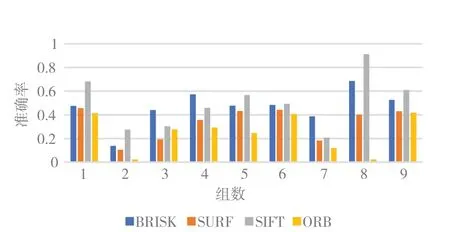
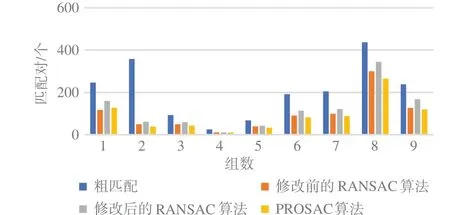
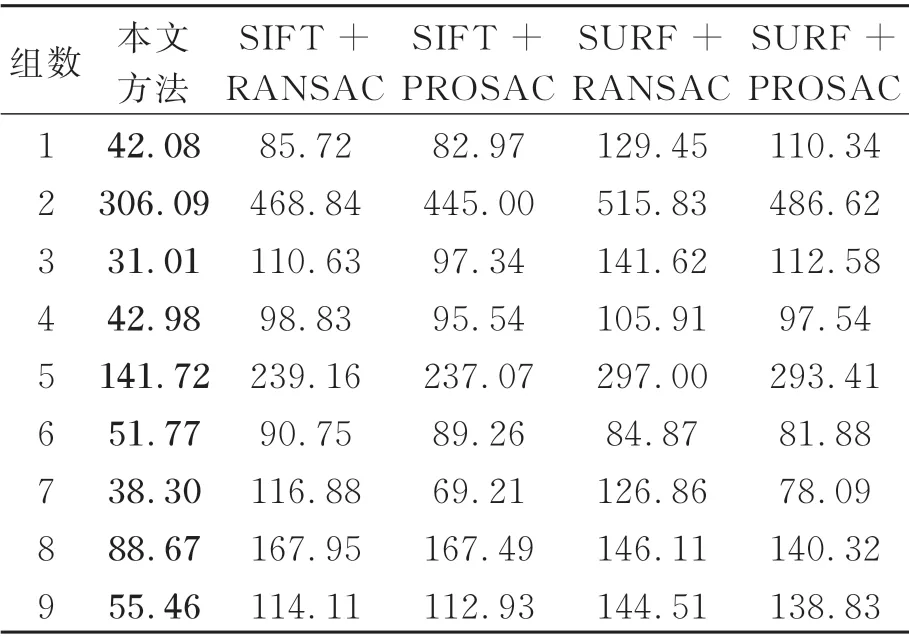
A={(Pi,Pj)∈R2×R2∣i≤N,j (2)式中,R2代表二元组,Pi、Pj为60 个采样点中的一个。在BRISK 中,根据采样点间的距离长短,从A中取出集合S和L。S和L的定义见式(3): 在单应性矩阵H中,h9是尺度,且恒为1,故共有8 个未知数。由上述式(8)~(13)知,一对映射点对可推导出两个等式,则至少需要4 对点就可以解出单应性矩阵H。换言之,要将一副图像投影变换为另一幅图像,至少需要知道投影变换前后4 对点的映射关系。 在计算单应性矩阵H时,如果已知的映射点对只有4 对时,可通过上述公式直接求解出H的值;但当对应点超过4 对时,可使用最小二乘法,使得反向投影错误率的值最小,来拟合求解单应性矩阵H,反向投影错误率的求解过程见式(14): 式中:h1……h9为对应的单应性矩阵H的9 个值,x'i、y'i为变换后的特征点坐标值,x'i为横坐标,y'i为纵坐标。xi、yi为变换前的特征点坐标值,xi为横坐标,yi为纵坐标。 由于输入的两幅图像存在亮度等方面的差异,在完成图像拼接后,新生成的图像会存在明显的拼接痕迹,影响视觉直观效果,需要采用加权平滑算法来实现两幅图像间的融合过渡。融合方法见公式(15): RANSAC 算法的主要作用是剔除掉特征点错误匹配对,算法所对应的流程图如图1(a)所示。其主要步骤为: 图1 改进前后的RANSAC 算法Fig. 1 RANSAC algorithm before and after improvement (1)从粗匹配结果中,随机的选取4 对非线性特征点匹配对组成集合M; (2)使用集合M计算出单应性矩阵H; (3)使用H对粗匹配结果中的所有匹配对进行验证,统计内点个数(内点为小于预设阈值的匹配对); (4)若当前内点数大于当前最优单应性矩阵的内点数,则对当前最优单应性矩阵进行更新,反之,不更新; (5)根据当前最优单应性矩阵的内点数更新迭代总次数,若当前迭代次数小于总迭代次数,返回执行步骤(1),反之,则当前最优单应性矩阵为最终结果。 根据上述的RANSAC 算法可知,在粗匹配的结果中匹配到的内点数越多,则认为当前模型越好,所以可以通过循环增大集合M,使其可以拟合更多的匹配点对,从而使得最终结果可以计算到更多的匹配对,故将算法做以下改进,算法所对应的流程图如图1(b)所示。 (1)从粗匹配结果中,随机的选取4 对非线性特征点匹配对组成集合M; (2)使用集合M计算出单应性矩阵H; (3)使用H对粗匹配结果中的所有匹配对进行验证,将内点加入到集合M中; (4)若集合M的点对数增加,则返回步骤(2)继续执行;若集合M保持不变,则执行步骤(5); (5)若集合M的点对数大于当前最优单应性矩阵的点对数,则对当前最优单应性矩阵进行更新,反之,不更新; (6)根据当前最优单应性矩阵的内点数更新迭代总次数,若当前迭代次数小于总迭代次数,返回执行步骤(1),反之,则当前最优单应性矩阵为最终结果。 在RANSAC 算法中,判断一个匹配对是否为内点(正确匹配对)的依据是:像素点(X,Y)经过单应性矩阵H投影变换得到的值与实际值的差应小于等于阈值。 当阈值取到足够大,接近无穷,那么此时任意选择的4 个初值所求出来的结果都将使匹配对满足情况,均被置成内点,无法达到将错误匹配对剔除的目的,从而导致最终拼接效果不佳。 当阈值取到足够小,甚至是等于0 时,则此时将会使绝大部分匹配对都不满足情况,满足情况的匹配对将会变得寥寥无几,并且将大部分正确匹配对剔除,使得最终内点结果占实际正确匹配对的比例太低,得到的内点将无法代表整体正确匹配对,使得结果的偶然性增大,导致拼接效果不佳。 当阈值取到合适值时,此时错误匹配对将会被剔除,正确匹配对被置成内点保留,且内点结果占实际正确匹配对的比例较高,可用得到的内点代表整体正确匹配对,使得最终效果更佳。 为了提高单应性矩阵的准确度,必须选择合适的阈值。由于在特征点检测BRISK 算法中得到的特征点的像数值是近似值而非精确值,所以此时就必须允许误差的存在。虽然得到的像数值是近似值,但由BRISK 算法可知,该近似值与精确值的差距在一个像素之内,故将阈值设置为1,且需将原内点判定方法由欧式距离改为面积判断,即将式(16): 实验在Python3.7 和Opencv3.4.5 下完成,硬件环境为:Windows10操作系统,主频2.20 GHz的Core i7-8750H 处理器、内存为8 GB 的笔记本电脑。本文共设计了3 组实验:实验一用于验证BRISK 算法相对于SURF 算法、SIFT 算法以及ORB 算法在特征点检测时间以及特征点匹配准确率上的优势;实验二用于验证本文改进的RANSAC 算法相对于传统RANSAC 算法以及PROSAC 算法在特征点匹配对和平均反向投影误差上的优势;实验三用于验证本文所使用的算法相对于其他常用算法的整体执行时间优势。 本文的实验数据来源包括两部分:自主拍摄和网上收集。实验数据共有18 幅图像,分为9 组,内容包括人物、楼宇、道路、自然风景等。 首先读入一组图像,对图像使用BRISK 算法进行特征点提取,对得到的特征点使用KNNmatch 进行初始匹配,由于粗匹配的结果中依然含有错误匹配对,无法直接使用最小二乘法来计算单应性矩阵H,因此还需将匹配结果通过RANSAC 算法进行错误匹配对剔除,再将精匹配结果使用最小二乘法求得单应性矩阵H,最后根据求得的矩阵H对图像进行转换拼接融合。流程图如图2 所示。 图2 实验流程Fig. 2 Experimental process 4.3.1 特征点的正确匹配对的数量 使用RANSAC 算法进行特征点错误匹配对剔除时,不仅会剔除掉错误的匹配对,同时也会将部分正确的匹配对进行剔除,尤其是在阈值要求严格的情况下,更容易将正确的匹配对进行误剔除。即在计算单应性矩阵H时,使用到的正确匹配对是整体的一部分,这一部分正确匹配对的数量越大,越可以代表整体正确匹配对,所以相对保留的正确匹配对越多越好。所以在阈值要求严格的情况下,特征点的正确匹配对数量越多,得到的单应性矩阵H越准确。 4.3.2 平均反向投影错误率 平均反向投影错误率可用来评估算法的匹配精度。平均反向投影错误率的计算式见式(18): 4.4.1 实验一 该实验的设计目的为验证BRISK 算法相对于SURF 算 法、SIFT 算 法 以 及ORB 算 法 的 优势。实验结果如图3、图4 所示。 图3 各算法提取特征点的时间对比Fig. 3 Time comparison of feature points extracted by each algorithm 图4 各算法的特征点匹配准确率Fig. 4 Matching accuracy of each keypoint detection al⁃gorithm 图3 的 折 线 图 是 由BRISK 算 法、SURF 算法、SIFT 算法以及ORB 算法对图像进行特征点检测所需时间的比较,各种算法的运行时间为10 次执行时间取平均值为结果。由图3 的各种特征点检测算法的时间对比结果可以发现,ORB算法的执行时间最少,BRISK 算法的执行时间低于SURF 算法、SIFT 算法,为次优结果。 图4 的柱状图是由BRISK 算法、SURF 算法、SIFT 算法以及ORB 算法对图像进行特征点匹配后,得到的特征点匹配准确率,其中特征点匹配准确率为经过RANSAC 算法得到的匹配对个数除以粗匹配对个数。由图4 可知,在当前阈值下,ORB 算法的匹配准确率最低,尤其在第2、8 组数据上,匹配准确率仅有0.02;BRISK 算法的匹配准确率在各组数据上均优于SURF 算法、ORB 算法,在第3、4、7 组数据上优于SIFT 算法。 由图3、图4 可知,虽然BRISK 算法的执行时间稍弱于ORB 算法,但其在匹配准确率上有着更为优秀的结果。BRISK 算法在执行时间和匹配准确率上均优于SURF 算法。与SIFT 算法相比,BRISK 算法虽然只有3 组数据在匹配准确率上占优势,但是在执行时间上各组数据均优于SIFT 算法,总体上可认为BRISK 算法优于SIFT算法。综上,在当前阈值下,BRISK 算法相对于SURF 算 法、SIFT 算 法 以 及ORB 算 法 具 有 明 显的优势。 4.4.2 实验二 该实验的设计目的为验证本文改进的RANSAC 算法相对于传统RANSAC 算法以及PROSAC 算法的优势,实验结果如图5 和表1所示。 图5 特征点的正确匹配对数目的比较结果Fig. 5 Comparison of the number of correct matching pairs of keypoints 图5 柱状图是经过剔除错误匹配对算法后保留的特征点最终匹配对数。粗匹配为经过KNNmatch 匹配算法得到的匹配结果,传统的RANSAC 算 法、改 进 的RANSAC 算 法、PRO⁃SAC 算法分别为将粗匹配结果经过对应的算法得到的最终正确匹配对个数。从图5 中数据可以发现,在每一组中,都剔除掉了大量的错误匹配对,但改进后的RANSAC 算法所保留的正确匹配对的个数大于传统的RANSAC 算法的结果,也大于PROSAC 算法的结果。 表1 是经过剔除错误匹配对算法后计算得到单应性矩阵H,再利用其求得平均反向投影错误率的结果,传统的RANSAC 算法、改进的RANSAC算法、PROSAC 算法分别为经过对应算法求得的平均反向投影错误率。从表1 中数据可以发现,在每一组中,改进后的RANSAC 算法得到的平均反向投影错误率小于传统的RANSAC 算法,同时也小于PROSAC 算法的结果。由实验数据可知:相对于传统的RANSAN 算法,本文改进的RANSAC 算法在平均反向投影错误率减少了约10%。 表1 平均反向投影错误率的比较结果Tab.1 Comparison of the average back-projection error rate 如图5、表1 所示,改进的RANSAC 算法的在特征点的正确匹配对数目和平均反向投影错误率上都具有优越性。以图像组数1 为例,其对应的图像处理过程如图6 所示。 由图6(d)可以发现,经过特征点粗匹配后,匹配结果中存在部分错误匹配对;图6(e)、(f)、(g)分别为粗匹配结果使用改进后的RANSAC算法、传统的RANSAC 算法以及PROSAC 算法进行剔除后的结果,括号内的数值为匹配对个数。可以发现,改进后的RANSAC 算法得到的结果均为正确匹配对,且数量上优于传统的RANSAC 算 法 和PROSAC 算 法;由 图6(c)可知,最终得到的拼接结果过渡较为自然,无明显接缝。 图6 图像拼接比较Fig. 6 Image mosaicing comparison 4.4.3 实验三 为了验证本文算法在时间方面的有效性,本实验将本文所用方法与较为常用的SIFT+RANSAC 方法、SIFT+PROSAC 方法、SURF+RANSAC 方 法、SURF+PROSAC 方 法 进 行 图像拼接的整体时间比较,整体时间主要包括特征点检测时间、特征点粗匹配时间、精匹配时间以及图像投影变换时间。实验结果如表2 所示,其中各拼接方法执行时间为10 次执行时间取平均值的结果。 从表2 中数据可以发现,本文的图像拼接方法的执行时间优于SIFT+RANSAC 方法、SIFT+PROSAC 方法、SURF+RANSAC 方法、SURF+PROSAC 方法。本文的图像拼接方法的时间占比约为上述方法的50%,尤其是在第3 组和7 组数据上,执行时间仅为其他算法的1/3,体现了本文方法的优越性。 表2 各拼接方法执行时间比较Tab.2 Comparison of execution time of each algorithm(ms) 针对图像拼接的特征点检测时间优化和最终匹配对优化问题,本文提出了一种图像拼接方法。该方法先使用BRISK 算法进行特征点检测,有效缩短了特征点检测的运算时间;然后改进了RANSAC 错误匹配对剔除方法,使得在相同的条件下,可以得到的内点数大于原RANSAC 算法,从而提高图像拼接的准确度。实验结果表明,BRISK 算法相对于SURF算法、SIFT 算法以及ORB 算法在特征点检测时间以及特征点匹配准确率上具有优势;本文改进的RANSAC 算法使得内点个数增加,平均反向投影错误率相对于原算法减小了10%左右;本文提出的拼接方法的执行耗时约为常用的SIFT+RANSAC 方 法、SIFT+PROSAC 方 法、SURF+RANSAC 方法、SURF+PROSAC 方法的50%。本文提出的方法能够实时、准确地进行图像拼接。 本文提出的算法主要针对于两幅图像的拼接,对于多幅图像拼接问题还需要更多深入的研究,如多幅图像拼接的图像曝光补偿等问题。

2.2 单应性矩阵的求解

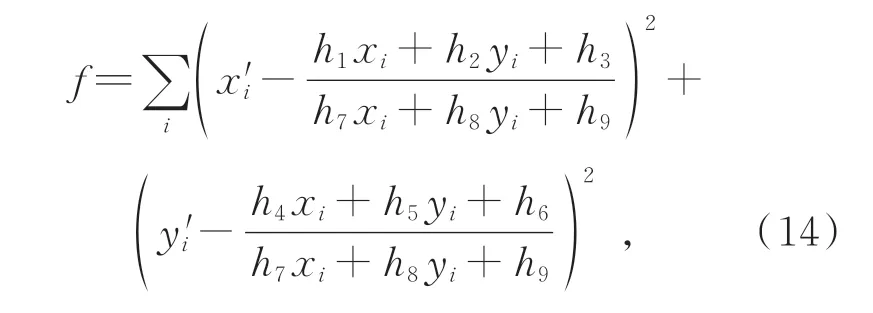
2.3 加权融合

3 基于RANSAC 算法的改进
3.1 传统的RANSAC 算法
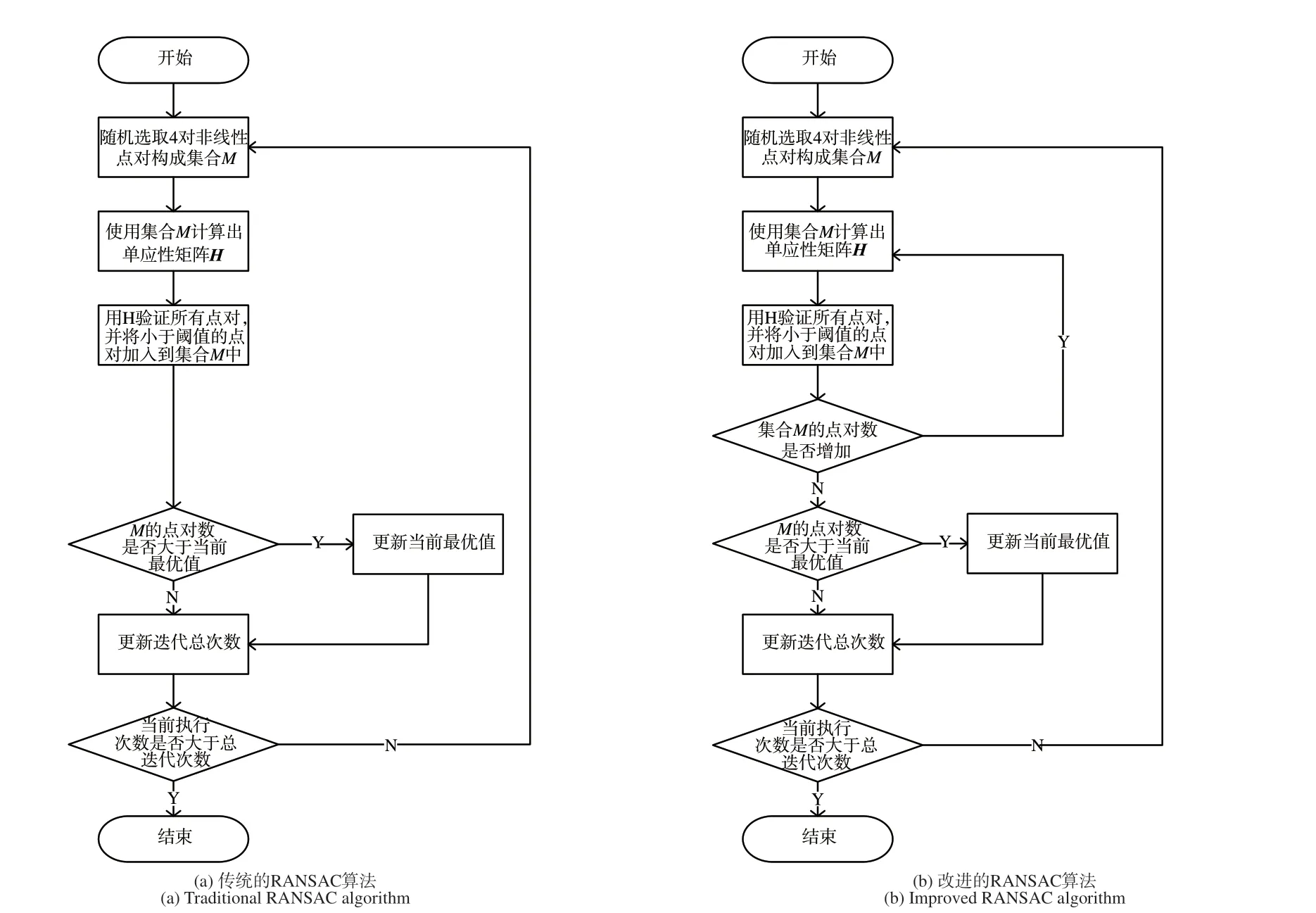
3.2 改进的RANSAC 算法
3.3 RANSAC 算法中阈值的选择

4 实验方案与分析
4.1 实验数据
4.2 实验流程

4.3 匹配精度评价指标

4.4 实验结果分析



5 结 论

