基于贝叶斯估计的故障电流过零点预测

刘云飞，周启文，方太勋，2

（1.南京南瑞继保电气有限公司，南京 211102；2.南瑞集团有限公司（国网电力科学研究院有限公司），南京 211106）

0 引言

随着新型电力系统的发展，电网故障电流水平持续攀升，导致断路器开断能力不足，严重影响电网安全稳定运行，成为制约电力建设和地区经济发展的瓶颈［1-2］。传统故障电流限制措施从优化电网结构、调整运行方式、安装高阻抗设备等方面考虑，对电网运行的灵活性与经济性都会带来不同程度的负面影响。近年来，基于智能快速断路器的故障电流抑制技术已发展成为一种新的针对故障电流超标问题的治理措施［3-5］，通过在故障后快速重构电网拓扑以增大系统阻抗，达到降低故障电流的目的。智能快速断路器一般采用斥力机构驱动真空断路器实现快速性的要求［6-8］，但目前商用真空断路器的额定开断电流最大仅有50 kA，同样存在开断能力不足的问题，在某些应用场合难以满足应用需求。相控开断技术通过预测故障电流过零点以控制断路器的动作时刻，可有效控制燃弧时间，减小触头电侵蚀，提高断路器开断能力，同时对提升断路器的可靠性和寿命具有十分重要的意义。

故障电流过零点预测算法的关键在于电流幅值、相位和衰减直流分量等状态变量的快速估计，其中预测时间、预测误差和算法复杂度是评价算法优劣的重要指标。目前电力系统广泛采用全波傅式算法或者半波傅式算法提取故障电流特征量，但在处理含衰减直流分量的电流波形时误差较大。文献［9］提出了基于安全点算法的相控开断方法，即忽略故障电流衰减直流分量的变化，以安全点代替实际电流过零点，同样存在预测误差较大的问题。文献［10-11］提出了基于RLS（递推最小二乘法）算法的故障电流参数提取方法，即以均方误差为代价函数拟合故障电流波形。文献［12-15］提出了基于自适应神经网络算法、WLMS（加权最小均方差）算法、自适应Prony 算法等的故障电流参数提取算法，这些算法通常均需要在线进行矩阵运算，计算量大且需存储大量采样数据，在边缘计算中对处理器性能提出很高的要求。

本文研究了基于贝叶斯框架的卡尔曼滤波和粒子滤波在故障电流过零点预测中的应用，通过对故障电流衰减时间常数的不同处理策略建立故障电流模型，提出扩展卡尔曼滤波、标准卡尔曼滤波和粒子滤波3种算法及其实现，最后通过算例仿真对比分析了算法的预测结果。

1 故障电流过零点预测

1.1 贝叶斯估计

贝叶斯估计将状态估计视为一个概率推理过程，即将估计问题转化为利用贝叶斯公式求解后验概率密度，包括预测和更新两个过程，预测过程利用系统模型预测状态的先验概率密度，更新过程利用最新的量测值进行修正，得到后验概率密度。

卡尔曼滤波是一种基于一阶马尔科夫模型的贝叶斯估计，其最大优点在于计算量小，能够利用前一时刻的状态和量测值递推计算当前时刻状态的最优估计。假设线性系统动态方程表示为：

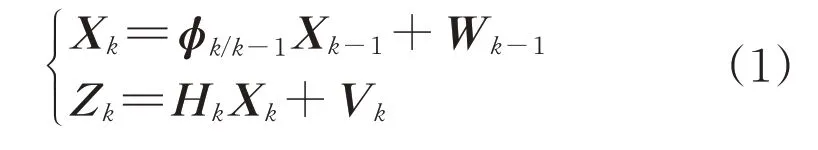
式中：Xk为n×1维的状态向量；Zk为m×1维的量测向量；Φk/k-1、Γk/k-1、Hk是已知的系统结构参数，分别为n×n维的状态一步转移矩阵、n×l 维的系统噪声分配矩阵和m×n维的量测矩阵；Wk为l×1维的过程噪声向量；Vk为m×1 维的量测噪声向量。两者都是零均值的高斯白噪声向量序列，且它们之间互不相关。

标准卡尔曼滤波过程可由以下方程进行递推求解：

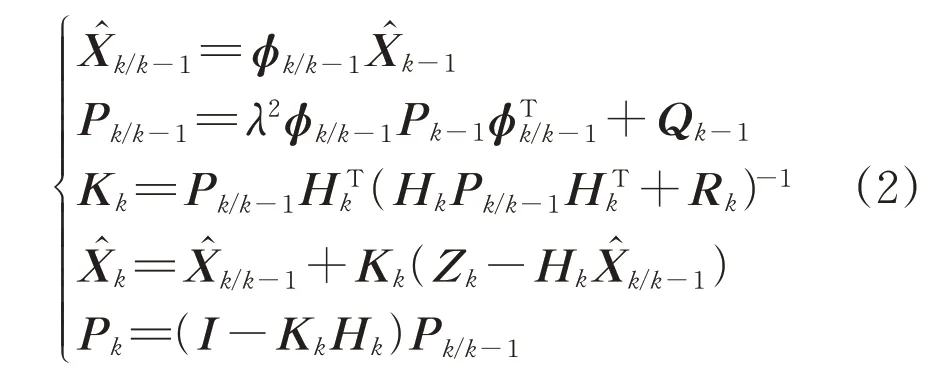
式中：λ为衰减记忆因子。当λ＞1 时，表示状态估计过程更依赖于量测值，以解决由模型误差带来的估计发散问题。

粒子滤波通过非参数化的蒙特卡洛模拟方法来实现递推贝叶斯估计，适用于任何能用状态空间模型描述的非线性系统，精度可逼近最优估计［16］。粒子滤波以有限个参数来近似后验，后验分布的样本叫作粒子，一个粒子就是根据真实世界状态在时刻t的一种可能假设。根据序贯重要性采样原理，假设后验概率为，在重要性分布中采样获得一组M个离散样本点，则可以得到粒子的重要性权重：

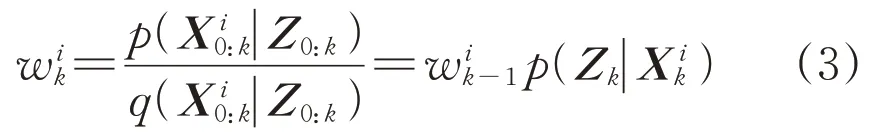
经过归一化得到，进而通过重采样得到状态估计值：

1.2 故障电流模型

电网故障电流主要由基波、谐波、衰减直流分量等成分组成，电流量测方程可以表示为：

式中：N为总谐波次数；In为n次谐波电流幅值；φn为n次谐波电流相位；I0为故障电流直流分量初值；τ为故障电流衰减时间常数；ω为电网频率；v（t）为电流量测噪声。

在故障期间可以认为电网频率为已知量，即保持工频不变，若选取In、φn、I0、τ分别作为未知状态变量，并假设各状态量在计算过程中保持不变，则状态方程为线性方程，而量测方程为非线性方程。其中非线性项由直流分量的衰减时间常数τ引起，对于该非线性项的处理是故障电流状态估计的难点。

采用卡尔曼滤波估计故障电流状态变量，但卡尔曼滤波的局限性在于其只适用于线性系统，因此需要将非线性系统近似为线性系统，即扩展卡尔曼滤波，采用一阶泰勒级数展开进行线性化处理。另一方面，根据电路原理，衰减时间常数τ主要由网架拓扑结构即电网等值电抗L和等值电阻R决定，对于某一运行方式下的区域电网，其故障电流衰减时间常数τ一般可认为是常数。因此可以借助数字孪生电网或者离线仿真等技术事先求解，此时量测方程即为线性方程，进而采用标准卡尔曼滤波即可估计故障电流状态。同时，由于粒子滤波处理非线性问题的优越性，采用粒子滤波进行故障电流状态估计成为另外一种可行的方法，此时将不需要对系统动态方程作任何处理。文中对这3种算法分别进行分析讨论。

1.3 状态估计算法

1.3.1 扩展卡尔曼滤波算法

采用扩展卡尔曼滤波进行故障电流状态估计，选取In、φn、I0、τ作为状态变量，状态转移矩阵Φk/k-1为单位矩阵，采样周期为Δ，根据故障电流模型和系统动态方程可以得到：

递推估计出状态变量Xk后，即可根据式（6）计算故障电流各次谐波幅值和相位、衰减直流分量，计算公式如下：

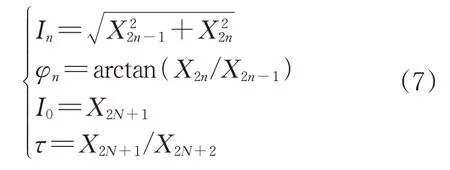
由于一阶泰勒级数展开引入截断误差，需要对非线性项I0和τ的估计结果进行修正，即根据拟合的随计算窗口时间变化的校正系数补偿线性化带来的估计误差。

1.3.2 标准卡尔曼滤波算法

采用标准卡尔曼滤波进行故障电流状态估计，选取In、φn、I0作为状态变量，将衰减时间常数τ作为已知常数，此时状态估计结果的准确性将直接取决于衰减时间常数τ。同样，根据故障电流模型和系统动态方程可以得到线性方程如下：

卡尔曼算法涉及矩阵运算，然而，由卡尔曼状态估计方程可知，在初始条件确定的情况下，矩阵Pk/k-1、Kk、Pk的计算仅由系统参数Φk/k-1、Hk、Qk、Rk决定，与量测值Zk无关。因此可以采用离线、在线相结合的计算策略，事先对卡尔曼增益Kk和量测矩阵Hk进行离线计算，计算结果作为宏参数保存在内存中，当系统实时运行时直接调用，不同通道的状态计算过程可以复用参数。进一步地，由于状态转移矩阵Φk/k-1为单位矩阵，卡尔曼状态估计方程的在线实时计算过程可以简化为仅对的递推求解。式（9）给出了电流状态量离散计算过程。

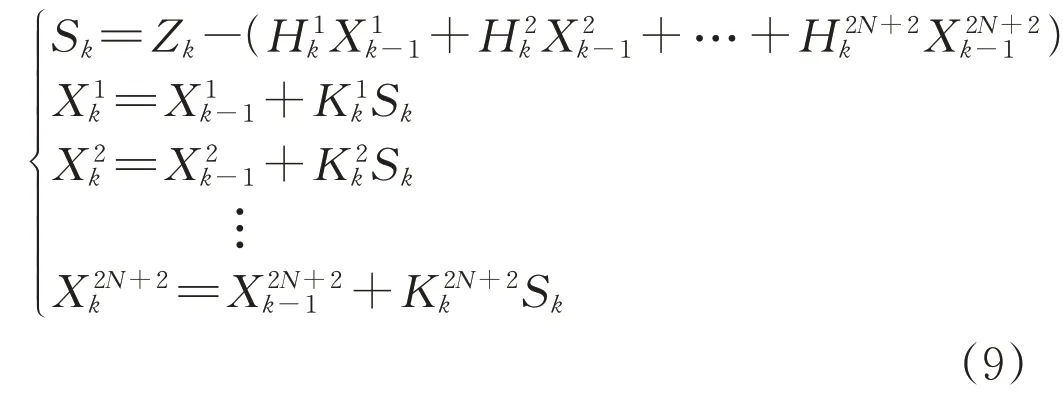
式中：下标表示第k个计算时刻；上标表示对应向量的第n个元素；Zk为第k个时刻电流采样值。

可以看到，电流单个状态量的计算平均仅需两次加法和两次乘法，计算量远小于其他故障特征提取算法。目前电力系统控制保护装置采样及程序执行周期一般为833 μs（常规保护装置）或者100 μs（故障限流控制装置），CPU 主频通常可以达到几百至上千兆赫，因此上述卡尔曼算法对控制保护装置负载率不会产生明显影响。

卡尔曼状态估计中P0、Q、R等参数影响状态估计性能。协方差矩阵P0为系统对初始状态X0的置信度，由于通常X0无法准确获取，P0取值应尽量大，以加快状态估计过程的收敛速度，本文取P0=κ×diag（a1，a2，…，an），其中κ为常数。协方差矩阵Q表示模型误差，例如模型的线性化、离散化误差等；协方差矩阵R为量测误差，与传感器的特性相关。这两个参数通过影响卡尔曼增益K的值，进而影响预测值和量测值的权重。在不知道P0、Q、R的准确先验信息的情况下，应适当增大Q的取值，以增大对实时量测值的利用权重，进而根据准确度、动态性能等要求进行调整。

1.3.3 粒子滤波算法

由于标准粒子滤波在低信噪比条件下可能出现估计结果发散的情况，本文针对状态方程为线性、量测方程为非线性的情况采用粒子滤波混合卡尔曼滤波的方法求解，即先采用标准粒子滤波对状态变量进行预估计，由于状态方程为线性方程，进而可以通过卡尔曼滤波进一步估计。

当观测噪声较大时，后验概率存在误差Ek，因此可以将作为量测值，构建如下的线性系统：

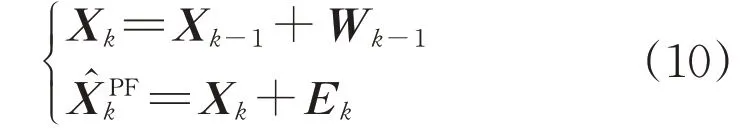
对此线性系统采用标准卡尔曼滤波再次进行状态估计，得到最终估计值。

在故障电流状态估计时，选取In、φn、I0、τ作为状态变量，此时无需对故障电流量测方程进行线性化处理，只需要选取一组状态量的样本点进行递推求解。

假设粒子数为M，状态变量个数为2N+2，生成初始粒子、生成高斯分布随机数、计算先验概率和重采样的计算量分别为A1、A2、A3、A4，则粒子滤波的时间复杂度可以表示为：

可以看到，与卡尔曼滤波相比，粒子滤波的计算量大大增加，且主要取决于粒子数。粒子滤波算法通常要求采用高性能DSP（数字信号处理器）或FPGA（现场可编程门阵列）来实现，并需要进行算法的优化设计，对控制保护装置的计算能力要求较高。

计算出故障电流模型参数In、φn、I0、τ后，可由式（5）中的故障电流模型直接预测未来一段时间内的电流值，然后根据二分法搜索故障电流第一、第二等过零点时刻，根据断路器分闸时间和燃弧时间计算相控开断所需等待时间。所述相控开断过程如图1所示。图1中：T0为故障发生时刻；T1为检测出故障、状态估计开始时刻；T2为状态估计结束、预测故障电流时刻；T3为发出分闸指令时刻；T4为过零开断时刻。相应地，t1为故障检测时间；t2为状态估计时间；t3为等待时间；t4为断路器分闸和燃弧时间。相控开断技术通过过零点预测算法将开关设备的燃弧时间转化为控制保护装置的等待时间，因此不会增加继电保护或者限流设备的总体动作时间，对系统不会产生负面影响。

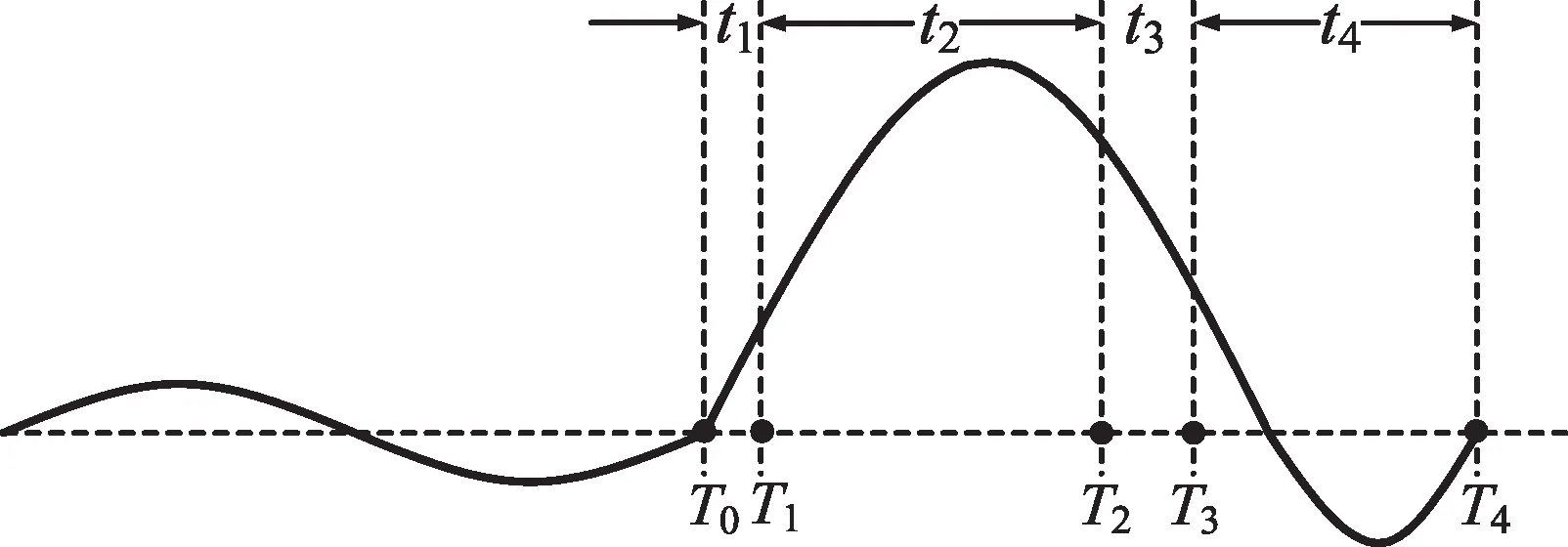
图1 故障电流过零点预测及相控时序

2 算例分析

假设故障电流量测值周期分量幅值为20 kA，相角为π/3，直流分量幅值为10 kA，衰减时间常数为45 ms，状态估计时长为40 ms。同时由于实际应用中采样、处理等环节引入的噪声，本文在电流波形中加入信噪比为40 dB的高斯白噪声，采样频率为10 kHz，分别采用上节所述扩展卡尔曼滤波、标准卡尔曼滤波、粒子滤波进行状态估计，同时与常规基于最小二乘法的故障电流特征参数提取方法进行比较，其中最小二乘法的故障电流模型与标准卡尔曼滤波模型保持一致，即满足式（8）。为减小计算量、加快状态估计收敛速度，本文故障电流模型中的周期分量仅考虑基波。同时，粒子滤波算法中，根据初始的量测值和量测方程开环计算出状态量的初始估计值，并在初始估计值附近按照20%计算误差的均匀分布产生初始粒子，粒子数取200。标准卡尔曼滤波算法中，衰减时间常数按照+10%的计算误差（即49.5 ms）进行估计。

图2 为几种算法关于In、φn、I0、τ这4 个状态变量的估计结果。随着时序数据的递推求解，4种算法最终均收敛于真实值，其中扩展卡尔曼滤波由于衰减时间常数收敛较慢，在15 ms左右时基本得到可用的状态估计值，此时4个状态量的估计误差分别为0.12%、2.15%、1.38%、0.93%，标准卡尔曼滤波和粒子滤波收敛时间分别为6 ms和10 ms 左右，对应误差分别为0.41%、2.26%、0.34%、10%和0.24%、1.33%、2.70%、0.46%，最小二乘法收敛过程与标准卡尔曼滤波基本相同，但误差比标准卡尔曼滤波要大，分别为0.74%、2.86%、1.44%、10%，这是由算法的特性所决定的，即最小二乘法作为卡尔曼滤波的特例，不考虑状态转移方程中的过程噪声，因此对于相同的线性模型，常以卡尔曼滤波作为状态的最优估计。当然，也可以采用最小二乘法求解式（6）中的故障电流模型，此时计算结果除误差较大外与扩展卡尔曼滤波算法也基本类似，此处不再赘述。

图2 4种算法估计的状态变量时序值

基于本文所提算法分别以3个时刻的状态估计值代入故障电流模型方程中预测未来一段时间内的电流波形，如图3所示。可以看到，3种算法预测的故障电流波形均与原始电流基本重合。

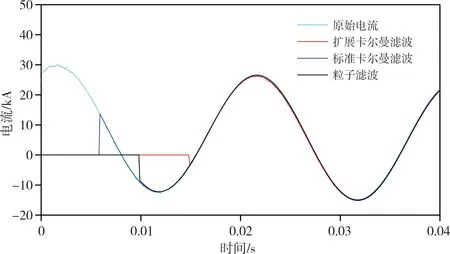
图3 贝叶斯估计算法预测的故障电流

在标准卡尔曼滤波算法中，由于衰减时间常数事先计算，其计算误差影响状态估计结果。本文为讨论衰减时间常数的计算误差对故障电流过零点预测结果的影响，分别选取了时间常数为45 ms、60 ms、90 ms、120 ms 和150 ms 时不同时间常数计算值引起的过零点预测误差，如图4 所示，其中误差取未来两个过零点中的误差最大值，每个点取10 次计算平均值。可以看到，总体预测误差均在2 ms 以内，取决于计算值偏离真实值的程度，考虑50%的时间常数计算误差时，过零点预测误差基本在0.5 ms 以内，且随着时间常数的增大，衰减特征更加明显，从而过零点预测误差也更小。

图4 不同衰减时间常数下的过零点预测误差

考虑5%的3次谐波和10%的5次谐波，同样采用上述只计及基波的策略进行估计，估计结果如图5 所示。可以看到，各状态变量最终均会收敛，但收敛时间增加，标准卡尔曼滤波收敛时间约10 ms，粒子滤波虽然快速收敛，但估计误差也有所增加，10 ms 时最大误差达到5%。扩展卡尔曼滤波对衰减时间常数的估计值在20 ms之后才逐渐稳定，考虑故障电流模型中的谐波分量后再次使用扩展卡尔曼滤波算法进行估计，结果如图5中的扩展卡尔曼滤波2曲线，在20 ms基本能够准确估计衰减时间常数在内的各个状态。可以看到，考虑故障电流模型中的谐波分量后可以提高状态估计精度，但也增加了算法复杂度，同时由于特征谐波次数与实际工况密切相关，需要根据实际应用折中取舍。

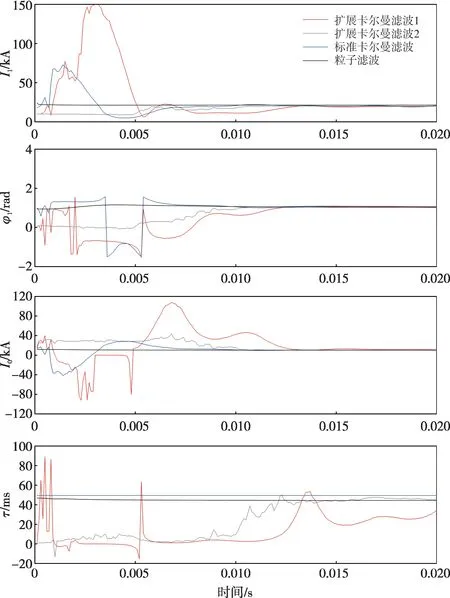
图5 加入谐波后贝叶斯算法估计的状态变量时序值

综上所述，标准卡尔曼滤波算法由于提前计算衰减时间常数这一非线性项，对其他状态量的在线估计速度较快；扩展卡尔曼滤波算法则适用于衰减时间常数无法提前计算且对收敛时间要求不高的场合；粒子滤波由于计算量大，在控制保护装置中的实现存在挑战。由于目前故障限流装置动作时间一般要求20 ms以内，常规保护装置出口时间一般在20 ms以上，因此以本文方法预测时间能够满足相关控制保护装置动作时间的要求。

3 结语

本文研究了基于贝叶斯框架的故障电流过零点预测算法，通过对非线性项的不同处理策略提出了扩展卡尔曼滤波、标准卡尔曼滤波和粒子滤波3 种算法及其实现。粒子滤波虽然整体性能较优，但存在计算量大的问题，在边缘计算中难以实现。而通过事先计算衰减时间常数进而采用标准卡尔曼滤波进行状态估计的方法可以快速预测故障电流过零点，且预测误差相对较小，具有工程应用价值。对于含有低频谐波的故障电流，在故障电流模型中考虑相应的特征次谐波，可以减小估计误差，但同时也将增加状态估计的计算量，需要在实际应用中综合考虑。基于贝叶斯估计的故障电流过零点预测算法在控制保护装置中的实现和验证工作有待进一步开展。