基于matplotlib的K-means-ARIMA模型对零售商品在传统节假日的销量预测
田歌 吴旷 田红蕊
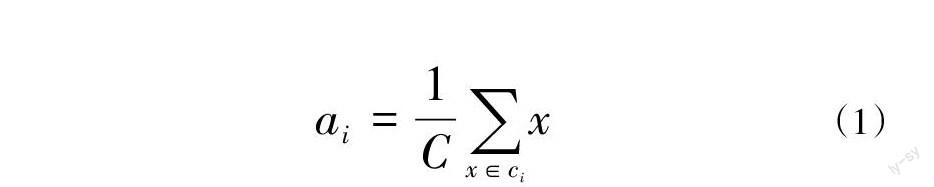

摘要:现多数的商品销量预测是以单个商品预测为主,而针对多类商品的销量预测如综合型商超或社区便利店来说存在一定的需求;同时对于县域或乡镇级商超,在传统节假日如春节期间出现大量返乡人员,由于人员数量激增,且春节具有走亲访友,互馈礼品的传统习俗,因此对各类商品的消费需求会在短时间内剧增,故对春节期间商品种类及销货数量的预测是商家及厂家备货的重要参考数据。本文基于以上两种现实需求对商品的种类和销量进行预测:由于不同类别商品销售量的波动会千差万别,如果使用所有的数据进行训练会对引入很多不必要的噪声,导致误差的增大,因此设计使用k-means聚类方法及ARIMA模型对多种商品在传统节假日期间的销量进行预测,在真实的某一典型县级商超销量数据库上进行评估验证,最后将其与基准的模型进行数据对比,以验证本方法对精度提升的度量。
关键词 :多类商品;传统节日;销量预测;K-means聚类;ARIMA模型
中图分类号:TP311 文献标识码:A
文章编号:1009-3044(2022)18-0059-02
开放科学(资源服务)标识码(OSID):
1引言
信息化的浪潮为商业带来了巨大的发展机遇,依据数据来驱动管理,指导决策极具商业价值,依靠智能运算对零售产品的销量预测估值已成为商家提高其竞争力的重要方式。根据对以往客户消费商品类别、数量、时间节点等大量信息,从中高效及时地预测客户需求,便于及时进行货品准备、推送广告及价格调整等后续准备动作的部署,为客户提升满意度,为商家创造更大的商业利润,同时也为避免商家因预测不准确导致的商业损失,帮助企业长期保持竞争优势。因此针对销售量的预测具有一定的商业和学术价值。
很多学者专注于该方向的研究突破以期得到更为准确或代价更低的计算方法。销量的预测大多数以时间序列进行,且以高聚合预测值为最终目标,对于低聚合的相关探究涉及不多,低聚合因素所产生的影响维度较多,天气、广告效果、促销等因素也是重要影响因素,如没有针对性去噪操作,会使损失一定的数据精度。常见的基于销售量的预测方法如ARIMA[1]和指数平滑法[2]等基于时间序列的预测已经得到大范围的使用。然单使用传统预测方法仅仅只能使用内部的变量进行预测,且一些非线性因素如上文提到的促销、广告等未能完全融合其综合影响,部分文献提出将线性因素使用ARIMA预测,非线性因素使用反向传播模型进行预测,结合二者优点,生成预测结果[3]。随着机器学习在各个领域的广泛应用,相继出现了多种结合机器学习的方法将时序预测模型转换为数据驱动及监督学习的方式,如将ARIMA与BP神经网络结合[4],支持向量机与ARIMA结合[5],ARIMA和XGBoost組合[6]卷积网络CNN与ARIMA结合,极限学习模型ELM与ARIMA结合等方式均能在不同层次不同行业领域内得出较理想的预测结果。除此之外也有不少的学者认为引入聚类模型可以大大的提升预测的精度效果,Venkatesh等使用聚类的方式预测ATM机的现金流量,根据其周季节特征进行聚类,在每一类上做神经网络训练,其实验验证了基于聚类的预测效果明显优于未实行聚类的效果[7]。目前大多数的预测都是基于单个商品,对于多类商品的销量预测相对不够广泛。本文以聚类模型将数据池中的数据分成一定的商品簇,通过ARIMA模型对每一商品簇进行销量预测,以此构建的多种类商品销量预测模型,将此模型与一般的ARIMA模型在同一数据池上进行测试,数据表明该模型具有较理想的预测效果。
2 K-means聚类算法
K-means即k均值算法的原理简单易且高效,因此在很多领域得到了广泛的应用[8],其主要思想是从数据样本中随机地选择k个初始点作为聚类的中心,[a=a1,a2,...ak];计算每个样本点[xi]到每个聚类中心[ai]的欧式距离,并将其分类到聚其最近的[ai]对应的类中,对每个类别[ai],再次计算其聚类中心公式为:
[ai=1Cx∈cix] (1)
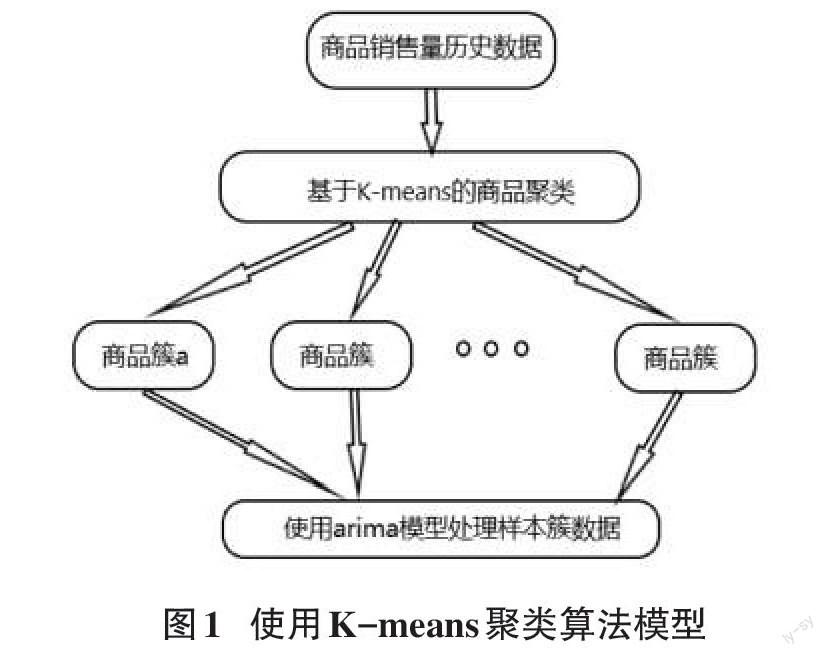
重复迭代以上步骤,直至聚心不再变动为止。我们以此为出发点,假设在商品销售历史数据中取时间点[Ti]为界,该界限前的销售量为样本训练数据,其余为测试数据
[d(s,Mj)=i=1T1(sj-Mij)](计算欧式距离)(2)
3 ARIMA模型
自回归移动平均模型(ARIMA也称Box-Jenkins模型)在1970年被BOX首次提出,该模型在基于对时间序列的数据分析中被广泛应用,主要研究某一种现象根据时间的不同所呈现的变化情况,因此不仅可以展示过去与现在的变化情况,也可以根据之前的数据分析、建模并预测出未来的变化趋势。
该模型将自回归、差分与移动平均线三种方法相结合,按以下步骤进行建模:
1)数据的平稳性检验与处理。平稳序列为某时间序列为一固定数值或在固定数值范围内波动,且延迟m期变量的自协方差与其自相关的系数ACF是基本相等的。平稳性即要求由样本的时间序列所生成的未来的拟合曲线依然可以按照现在的“惯性”往下延续,其均值与方差变动不明显。其检验方法大致分为主观图形检验、单位级根检验等。数据平稳性的处理一般使用d阶差分运算:将两个相邻时间段的序列值相减即为差分运算(一阶差分),将所得数值再次相减即为二阶差分,重复d次即为d阶差分。
2 )p和q定阶、参数估计。即根据ACF(自相关系数)和PACF(非自相关系数)趋向于0的方法进行定阶,一般选择部分时间序列进行计算,根据网格法遍历所有参数,然后用python对时间序列进行拟合,若预测序列图与实际序列图大致吻合,则对当前模型进行肯定。
3)残差检验(白噪声)。白噪声检验即检查一个序列中是否存在一定的关系,若没有任何关系,则称该序列为纯随机序列。检验方法为检查ACF是否趋近于0。
4)估算并预测。根据p、q、d等模型参数进行对未来时间序列的预测。
本文在jupyter平台完成代码的实现及数据处理与图形制作。
4使用jupyter平台使用matplotlib基于K-means和ARIMA模型进行预测
4.1数据来源
收集了一县域级小型商超在2017~2021年春节期间的商品销量记录。
4.2使用k-means进行聚类
聚类后将商品分为里三个商品簇:可概括为日用品、烟酒类及副食品等产品簇。
4.3对每个商品簇进行销量预测
4.3.1平稳性检验
本文使用ADF检验,该方法是判断一个序列中是否存在有单位根,如何一个序列是平稳序列,则没有单位根,在python中可通过模块statsmotels进行检验实现。导入数据后进行原始序列的ADF检验,结果为: (adf检验的结果:-3.0303619167579696, 统计量的P值:0.03215462767083654, 计算过程中用到的延迟阶数:5, 用于ADF回归和计算的观测值的个数:
31,{'1%': -3.661428725118324,'5%': -2.960525341210433,'10%': -2.6193188033298647}, 426.8275356961312)是配合adf检验的结果一起看的,是在0.99,0.95,0.90置信区间下的临界ADF检验值。
一阶差分序列的白噪声检验结果为: (array([8.41941052]), array([0.00371236]))。
4.3.2 定阶
分别使用AIC和BIC方法得到最优的p值和q值均是0和1。
4.3.3 建模与预测
5预测结果分析
表1为使用K-means模型聚簇后的arima预测与不使用K-means方法的预测结果对比,使用该方式在商品销量预测中具 有较高的准确率。本文所设计的预测方法不仅对商超零售具有一定的指导意义,对相似的基于时间序列的、销量预测也具有一定的参考价值,但由于K-means具有需要手动设置聚类的数值,因此或可尝试将更多的机器学习的方法融入其中,以期达到更优的效果。
参考文献:
[1] 姜晓红,曹慧敏.基于ARIMA模型的电商销售预测及R语言实现[J].物流科技,2019,42(4):52-56,69.
[2] 張蔚虹,刘立.指数平滑法在销售预算中的应用[J].中国管理信息化,2008,11(2):84-86.
[3] 闫博,李国和,林仁杰.混合销售预测模型[J].计算机工程与设计,2015,36(3):814-818.
[4] 朱家明,胡玲燕.基于ARIMA和BP神经网络对人民币汇率预测的比较分析——以美元人民币汇率为例[J].重庆理工大学学报(自然科学),2019,33(5):207-212.
[5] 刘家学,白明皓,郝磊.基于ARIMA-SVR组合方法的航班滑出时间预测[J].中国科技论文,2021,16(6):661-667.
[6] 谢学斌,孔令燕.基于ARIMA和XGBoost组合模型的交通事故预测[J].安全与环境学报,2021,21(1):277-284.
[7] Venkatesh K,Ravi V,Prinzie A,et al.Cash demand forecasting in ATMs by clustering and neural networks[J].European Journal of Operational Research,2014,232(2):383-392.[8] 李秉晨,于惠钧,刘靖宇.基于Kmeans和CEEMD-PE-LSTM的短期光伏发电功率预测[J].水电能源科学,2021,39(4):204-208.
【通联编辑:闻翔军】

