基于深度学习和不可分小波的裂纹检测方法

周圆昊 王震 郝昱权 刘斌

摘要：基础建设逐渐老旧、破败，产生了许多问题，裂纹是其中之一。在现有的裂纹检测方法上，如人眼检测和基于深度学习的裂纹检测，该文提出了一种将不可分小波与卷积神经网络相结合的新方法。首先构造二通道不可分小波滤波器组对数据集的图像进行低频提取，然后利用不可分加性小波的分解原理，得到高频图像数据集;再对DenseNet進行迁移学习构造神经网络;最后将高频图像数据集的80%用作训练集，20%用作验证集，放入神经网络中进行训练和验证。实验结果表明，该方法可得到较好的裂纹检测效果。

关键词：裂纹检测;深度学习;卷积神经网络;不可分小波;加性小波;迁移学习

中图分类号：TP181      文献标识码：A

文章编号：1009-3044（2022）18-0006-04

开放科学（资源服务）标识码（OSID）：

1 引言

随着社会经济的不断发展，我国的基础设施建设能力越来越强，基础建设程度也越来越发达。大量的基础设施会随时间推移而逐渐破败，产生许多安全隐患。裂纹便是一个重要问题。为了降低人工维护的成本，防患于未然，裂纹检测成了一项重要的技术[1-2]。

裂纹根据其所处位置不同主要分为内部裂纹和外部裂纹，本文聚焦于外部裂纹的检测。早期裂纹检测方法主要是人眼识别。这种方法主要有以下三个缺点：1）检测的结果会受到检测员的个人能力、环境气候等各种状况影响;2）检测员人工检测效率较低;3）人工检测的标准无法统一。

利用卷积神经网络进行图像裂纹检测解决了上述的三个问题，兼具较强的鲁棒性、高效率和客观性的特点，但根据方法的不同，会出现识别精度不高，图像质量的好坏严重影响检测效果，或是一些漏检、误检的情况[3-7]。

因此，本文提出基于深度学习和不可分小波的裂纹检测方法，利用不可分加性小波提取裂纹图像的高频部分，然后利用迁移学习构造卷积神经网络，再对裂纹图像进行检测，取代了效率较低的人眼识别，并对仅基于卷积神经网络的检测方法进行了优化。

2 相关知识简介

小波的出现使得提取图片的特征信息变得较为简单，裂纹图像中的低频和高频部分差别较大的特点尤其适合用小波来进行特征提取。

2.1 不可分小波介绍

不可分小波在图像处理中有着良好的特性。张量积小波是二维小波的特殊情况，二维不可分小波是近年来发展起来的一类新小波，它是二维小波更一般的情况，图像是二维信号，张量积小波是用点信息去逼近二维图像，而图像是二维曲面，只有使用真正的二维小波才能完全、更好地逼近它。另外，相较于张量积小波，不可分小波有很多优点，如可同时具有紧支撑、正交性和对称性，在对图像进行分解和重构时，能获得具有较高空间分辨率的图像，克服了张量积离散小波变换不能获得高空间分辨率图像的不足。已有的方法研究了基于四通道、三通道、二通道不可分小波滤波器组的构造，并把它们应用于图像处理中，获得了较好的效果。

在这三种方式中，二通道不可分小波有其明显的特色。1）一般景象的图像信息多集中在二维频谱的所谓钻石型区域中，采用五株型采样能较好地提取该区域内的信息，二通道不可分小波完全满足此要求;2）二通道小波只有两个通道，在对图像进行分解与重构时，只需做两个通道的滤波和采样[8]，相对于四、三通道不可分小波，它能减少许多运算量。

由于加性小波保留边缘特征较好，适合用于裂纹检测，所以本文采用了不可分加性小波进行分解和重构。

2.2 加性小波

加性小波本质为利用二维低通滤波器对图像进行átrous分解，利用滤波器对图像进行卷积，不进行抽样，得到小波平面系列;原图像即为小波平面之和与残余图像的相加。具体流程如下所示：

设[p0]为原图像，则：

[H0p0=p1，w1=p0-p1，H0（p1）=p2，w2=p1-p2，H0（p2）=p3，w3=p2-p3，......]                          （1）

其中[wi]为小波平面，[pi]为小波近似分量。其重构公式为：

[p0=i=1nwi+pr]                                    （2）

其中[pr]为残余图像。

2.3 卷积神经网络

近十年来，深度学习作为机器学习的分支，发展迅速，并且提出许多先进的算法，卷积神经网络就是其中一种。在裂纹检测领域，深度卷积神经网络（CNN）取代传统的机器学习已经成为发展的新趋势。CNN由多层卷积神经网络组成，每层又由多个特征图组成，其本质就是一种从输入到输出的映射，它依靠网络自身学习大量输入与输出之间的映射关系。同时CNN可以自动地提取图像中不同层次的特征，再根据这些特征进行分类或者识别等任务，可以较好地反映数据的本质。

2.4 迁移学习

迁移学习是机器学习的一个研究方向，主要研究如何将任务A上学习到的知识迁移到任务B上，以提高在任务B上的泛化性能[9]。例如，任务A是手机壳的划痕区分，需要训练一个分类器能够较好地区分手机壳的划痕和手机壳本身的图案，任务B是裂纹图像的检测，可以发现任务A和任务B存在大量的共享知识，裂纹和划痕比较相似，背景干扰项也有一定程度的相似。因此，当获得了一个任务A的训练器时，在训练任务B时不需要从0开始训练，在A训练器的基础上进行一定的调整即可。这样可以通过更少的样本和更少的训练代价，获得较好的泛化效果。迁移学习的结构如图1所示。

网络微调技术是常用的迁移学习方法。这种技术能逐层提取特征，越末层的网络，抽象提取的能力就越强，输出层则一般使用与类别数相同输出节点的全连接层，作为分布网络的概率分布预测。对于相似的任务，如果前面数层可以重用，则可以只将网络后面的数层根据任务设定从零开始训练。

由于迁移学习的高效性，本文選择利用迁移学习在一个较为成熟的神经网络（DenseNet）上进行使用，构造出适合的检测网络。

3 训练过程

3.1 数据集

笔者在网上下载了的5000张裂缝图像和5000张干扰图像，然后进行平移、翻转、缩放、旋转、调色、颜色增强、亮度增强、对比度增强等方式，最后获取了20000张裂缝图像和两万张干扰图像，其中各取4000张用作验证集，剩余16000张用作训练集。

3.2 模型架构

3.2.1神经网络的构造

神经网络的构造参考了DenseNet的文章[10]，并且对其进行了一定的优化，具体优化过程如下文所示：

将DenseNet最后的全连接层删除，并将DenseNet最后一个Pooling层设计为Max Pooling，然后增加一个输出节点为1024的全连接层。最后根据裂纹有无进行二分类，添加一个输出节点为2的全连接层。具体结构如图3所示：

其中圆1表示输入层，圆2、3、4表示卷积层，圆5表示转换层。

3.2.2不可分小波滤波器的构造

不可分小波滤波器的构造主要包括三个过程：采样、分解和重构。本文采用不可分加性小波，保留边缘特征用于裂纹检测，因此不进行采样。

Qiuhui Chen[11]等提出了高维具有正交性、紧支撑性的非张量积小波滤波器组的构造方法，其构造的高维低通滤波器[m0（ξ）]具有如下频域形式：

[m0ξ=1sXξj∈ZNUjDGATξ×j∈ZNUTN-1-jV0，ξ∈Rd]     （3）

其相应的[s-1（s=det（A））]个CQF滤波器的形式为：

[mj（ξ）=1sX（ξ）l∈ZN（UlD（ATξ））（l∈ZNUTN-1-l）Vj，  ξ∈Rd，（j=1，2，…，s-1）] （4）

笔者在此基础上构造二维二通道滤波器组。

设小波变换时伸缩矩阵为[111-1]，为构造二维二通道滤波器组，取[s=2]，构造：

[s=2，Xx，y=1，xy，DGx，y=100xy]则滤波器组形式可构造如下：

[m0x，y，m1x，y=12Xx，yj=1KUjDGx，yUTjV ，]       （5）

其中[x=exp（-iω1），y=exp-iω2]，[Uj（j=1，2，...，K）]为正交阵，V1为2×1向量，V0=（1，1）T。

为构造二通道6×6的二通道滤波器组，取K=4，得：

[U1=cosα1-sinα1sinα1cosα1，U2=cosα2sinα2-sinα2cosα2，U3=-sinα3-cosα3cosα3-sinα3，U4=sinα4cosα4-cosα4sinα4，V=111-1，]                    （6）

可以验证，[Uj]均为正交矩阵（[aj]为参量），[v2]为正交阵。据此可构造无穷多个滤波器组，[aj]取不同的值得到不同的滤波器组。笔者设计了一组具有紧支撑、正交性的小波滤波器组。为了获得具有对称的滤波器组，取[α1=3π/4]，[α2=π/2]，[α3=-π/4]，[α4=-π/2]代入式（3）可得：

[m0x，y=-0.125+0.375xy+0.25x2y2+0.250x3y3+0.375x4y4-0.125x5y5]，

其时域形式如下：

[H0=18-10000003000000200000020000003000000-1]                         （7）

显然，此滤波器是不可分的，不能分解为两个一维小波滤波器的张量积，因而它是二通道不可分小波滤波器组。

3.3实验方法及步骤

本实验的具体方法及步骤如图6所示：首先，输入图像，使用不可分小波提取图像低频部分，然后利用加性小波分解原理得到高频图像;再将高频图像随机分为训练集和验证集，接着，将训练集图像放入，利用迁移学习构造好的神经网络中进行训练;训练结束后再用验证集进行验证;最后，使用20张数据集以外的图片进行测试。

3.4结果分析

本文实验是在处理器为Intel（R） Xeon（R） Silver 4210 CPU @2.20GHz，内存为24G，显卡为NVIDIA Quadro RTX 5000的主机上进行的。

将图片进行不可分加性小波处理之后，随机分成两份，包括训练集32000张（16000张裂纹图像，16000张干扰图像），以及验证集8000张（4000张裂纹图像，4000张干扰图像），表1是学习率为[1×10-4]，Batch Size为16，训练20次的部分训练准确率和验证准确率。

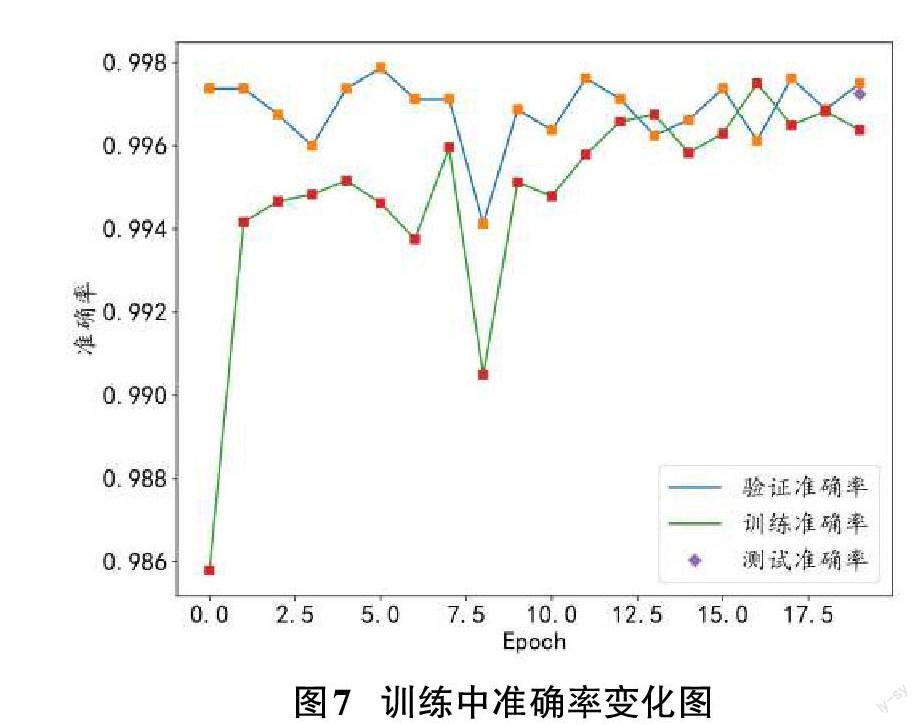
训练过程中准确率变化如图7所示。

由训练结果可知，在完成训练时准确率为0.9963750243，将模型进行保存（准确率：0.9963）。

3.4 调用模型预测实例

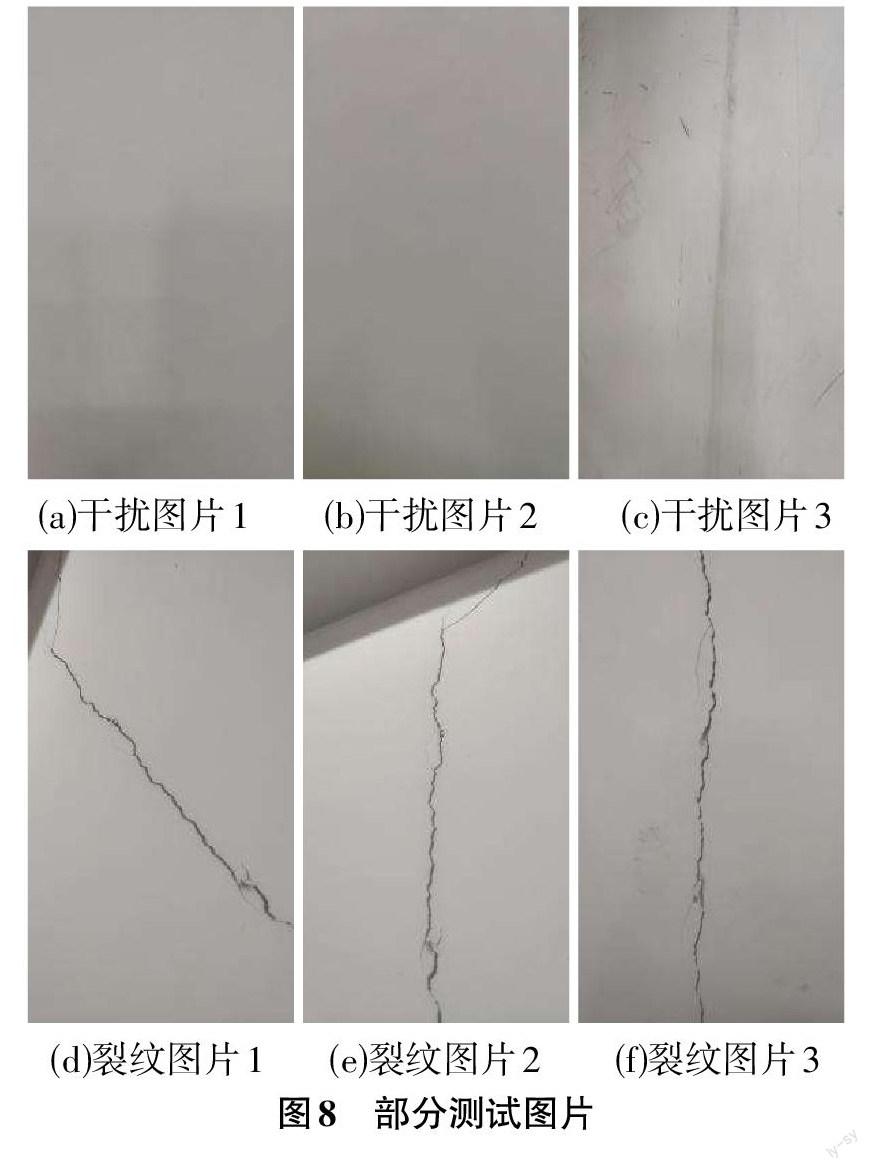
由于验证集数据与训练集数据存在相似性，为了测试神经网络模型的通用性，拍取了一些生活中的裂缝图像进行检测，总共20张。部分测试的裂纹图像如图8所示。

其中，图（a）、（b）、（c）为干扰图像，图（d）、（e）、（f）为裂纹图像。对拍摄的20张图像进行测试，得到最终的准确率为100%。

4 结论

本文提出了一种结合不可分加性小波和深度学习的裂纹检测方法。利用不可分加性小波提取图像高频的特点以及卷积神经网络的自主学习能力来进行裂纹检测。实现了不可分小波与深度学习相结合的自动化裂纹识别，并得到较好的裂纹检测效果。

参考文献：

[1] 王森，伍星，张印辉，等.基于深度学习的全卷积网络图像裂纹检测[J].计算机辅助设计与图形学学报，2018，30（5）：859-867.

[2] 程丰.基于计算机视觉的路面裂纹检测研究[D].北京：北京交通大学，2018.

[3] 冉蓉，徐兴华，邱少华，等.基于深度卷积神经网络的裂纹检测方法综述[J].计算机工程与应用，2021，57（9）：23-35.

[4] 王宪保，李洁，姚明海，等.基于深度学习的太阳能电池片表面缺陷检测方法[J].模式识别与人工智能，2014，27（6）：517-523.

[5] 林丽君，殷鹰，何明格，等.基于小波模极大值的磁瓦裂纹缺陷边缘检测算法[J].电子科技大学学报，2015，44（2）：283-288.

[6] 孙朝云，马志丹，李伟，等.基于深度卷积神经网络融合模型的路面裂缝识别方法[J].长安大学学报（自然科学版），2020，40（4）：1-13.

[7] 李良福，马卫飞，李丽，等.基于深度学习的桥梁裂缝检测算法研究[J].自动化学报，2019，45（9）：1727-1742.

[8] 刘斌，彭嘉雄.基于二通道不可分加性小波的多光谱图像融合[J].光学学报，2007，27（8）：1419-1424.

[9] 曲蕴慧，汤伟，成爽爽.基于深度卷积神经网络及迁移学习的纸病分类方法研究[J].中国造纸，2021，40（10）：63-70.

[10] Huang G，Liu Z，van der Maaten L，et al.Densely connected convolutional networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition.July 21-26，2017，Honolulu，HI，USA.IEEE，2017：2261-2269.

[11] Chen Q H，Micchelli C A，Peng S L，et al.Multivariate filter banks having matrix factorizations[J].SIAM Journal on Matrix Analysis and Applications，2003，25（2）：517-531.

【通聯编辑：唐一东】