球对称有限水体气泡振荡模型及其对陆地水体气枪研究的意义

徐逸鹤，王宝善，王伟涛

1 中国地震局地球物理研究所，北京 100081 2 英国剑桥大学地球科学系，剑桥 CB3 0EZ 3 爱尔兰都柏林高等研究院宇宙物理学学院地球物理学分部，都柏林 D02Y006 4 中国科学技术大学地球和空间科学学院，合肥 230026

0 引言

利用人工震源向地下发射地震波，是开展地壳及浅部成像的重要方法.在地震活动性较弱的地区，人工源探测可增加震源点位，提升成像所需的路径覆盖，服务相应的成像要求(陈颙和朱日祥，2005; Li et al., 2006; Etgen et al., 2009; Zhang et al., 2011).地震波的振幅会因为几何扩散和黏弹性衰减而随着传播距离减小，所以人工震源需要具有足够的能量来保证清晰的远距离或深部成像.炸药震源是人工震源的重要代表，其能量密度高，使用数百到数千公斤级的炸药可以获得近千公里地壳结构的成像(高锐等，2006；Zhang et al., 2011).但是由于炸药震源对环境的负面影响及本身的安全性问题，寻找替代震源成为了主动源探测的一个重要的研究方向(李丽等，2004；Alekseev et al., 2005; 罗桂纯等，2006；陈颙等，2007a；李稳等，2020).其中，之前用于海洋勘探的气枪震源具有能量大、重复性高、环境友好等特点，具有深部探测的潜力(Dragoset, 2000；丘学林等，2007；赵明辉等，2008；王伟涛等，2017；吴志强等，2019).

气枪震源通过在水体中瞬间释放预先充在气枪枪体中的高压(可达一百多个大气压)气体产生了类似于炸药水下爆炸所产生的高压气泡，进而引起水体振荡，产生地震波.气枪震源单次激发能量高，相当于0.5～1级的地震(张尉等，2009)，并且气枪震源具有很好的重复性，可以通过叠加多次激发的结果进一步提高探测距离(林建民等，2008；唐杰等，2009).目前，气枪震源已在不同陆地水体中有成功性的应用，包括在水库中的固定激发(陈颙等，2007b；Wang et al., 2012)以及在河中船拖拽的流动激发(田晓峰等，2016；张云鹏等，2016；徐逸鹤等，2016)，并获得了体波、面波走时层析成像的结果(田晓峰等，2016；张云鹏等，2016；She et al., 2018；Zhang et al., 2020).此外，得益于气枪震源的高重复性，气枪还可以进行精细的时变监测 (Wang et al., 2020).

对于气枪震源激发过程和气泡振荡的研究，是深化陆内水体气枪震源分析的重要方面.气枪震源的激发过程可以大致分为两个阶段：(1)枪体中高压气体通过气阀释放到水中，形成初始的高压气泡；(2)高压气泡在水中的自由振荡.第一个阶段会产生一个尖锐、高振幅的信号，通常称为主压力脉冲或主脉冲，而第二个阶段会产生一个振幅逐渐减小的周期振荡信号，称为气泡脉冲.同时，主脉冲和气泡脉冲在水面的反射会产生一个时间略微滞后的负脉冲信号.这三个脉冲信号构成了气枪震源源区信号的主要特征.

经典的气枪震源激发过程研究通常采用解析方法，优势是计算快速，缺点是需要事先评估气枪激发物理过程的影响因素的主次，然后进行合理的简化(Ziolkowski, 1970; Schulze-Gattermann, 1972; Ziolkowski et al., 1982; Laws et al., 1990; 王立明，2010).通常只考虑高压气泡的自由振荡阶段，而将高压气泡的形成阶段简化为气泡壁运动的初始条件，气泡上浮、变形等次要因素也予以忽略.模型核心是求解球形气泡在无限可压缩无黏流体中的振荡过程 (Lamb, 1923; Gilmore, 1952; Keller and Kolodner, 1956; Ziolkowski, 1970; Plesset and Prosperetti, 1977; Brennen, 2013; de Graaf et al., 2014).

经典气枪模型和实测海洋气枪信号有很好的一致性，说明相关简化符合海洋激发坏境中的实际物理过程.但是在陆内水体气枪研究中，观测到的陆内气枪源区信号与经典气枪模型的预测存在较大偏差(唐杰等，2009；唐杰，2010).该差别很可能是由于陆内水体较小而导致的，但是对于陆内水体如何影响气枪激发过程还缺乏系统的研究.通过数值模拟对不同水体形状、水深、气枪位置的模拟可以解释部分趋势，但是由于使用的是预设的子波，更多地关注压力波在水体中传播及其转换为地震波过程，不能研究有限水体对气泡振荡本身的影响(孙楠等，2017；胡久鹏等，2017)，因此无法解决临界水体大小的问题.

研究有限水体对气枪震源初始激发信号的影响是目前亟待解决的关键问题之一.在经典气枪理论的球对称气水双层模型基础上增加一层固体，即中心为球形气泡，中间层为球形水体(中空)，外层为无限大的固体，可以对有限水体中气泡的振荡进行研究.该模型也经过了适当简化，但这一简单模型的优点是可以避免其他因素的干扰，更准确地分析水体大小这一因素的独立影响.该有限水体气枪模型在水体半径足够大时，气泡振荡过程接近无限水体模型，而球腔半径逐渐减少时，固液界面的影响会逐渐增强.当气泡振荡过程开始与无限水体模型出现明显偏差时，可以将对应水体大小视为临界水体.当水体大于该临界大小时，可以使用经典气枪模型(无限水体)来模拟气枪信号的震源时间函数；当水体小于临界大小时，需要考虑有限水体对气泡振荡过程本身的改变.

利用解析方法求解该有限水体模型存在较大的困难，原因是固液边界的反射波使气泡振荡方程中出现了时延项.Doinikov等(2018)得到的有限水体模型的气泡振荡方程包括11项，比无限水体的气泡振荡方程增加了近2倍(4项)，且每一项的形式也更为复杂.此时使用理论解的难度已经高于数值解，并且理论解具有很弱的扩展性.

使用常规数值方法对该问题进行精确求解也同样存在一定的难度，包括：(1)气体、水体、固体满足不同的控制方程，且水体模拟多用欧拉描述，即同一位置在不同时刻的运动状态，而固体模拟多用拉格朗日描述，即同一质点在不同时刻的运动状态；(2)气水界面的高密度差、高压力差容易产生数值振荡；(3)精确地描述和追踪气水界面需要特殊的方法(如Level-set，Volume of Fluid等)；(4)气泡尺度(1 m)与模拟区域尺度(百米)相比相差较大；(5)气泡振荡过程的准确模拟通常需要以很小的时间步长(约10-5s)计算1 s (King, 2016)；(6)常规模拟方法多采用不可压缩流体，对高压气泡的振荡过程模拟可能不准确(董明荣等，2016).因此使用常规数值模拟方法不仅较难实现，计算量大，而且还可能会牺牲结果的精度.

采用欧拉有限元通过组合拉格朗日和欧拉描述，可以对水下爆炸产生的高压气泡进行较好地模拟(Liu et al., 2018b). 该方法的第一步是采用拉格朗日描述的有限元方法对流体力学方程在轴坐标下进行求解.本研究利用有限水体气枪模型的球对称属性，在球坐标下重新推导了有限元数值格式.由于水体在有限的空间内振荡，用拉格朗日有限元替代欧拉有限元，进一步简化了问题的求解.由于气泡也为球对称，可以将模拟区域的边界设在气液边界和固液边界上，既将三种介质的模拟简化为单一介质的模拟，又可以精确、显式地追踪气泡(即气液边界)的变化.气泡和固体的作用以边界条件的形式施加在水体上.

本文将介绍水体控制方程及其球对称条件下拉格朗日有限元的推导过程，并以此分析气泡半径的振荡曲线、气泡振荡周期和振幅与水体大小的关系以及气枪振荡过程受影响的机制.通过数值模拟方法，对气枪在有限水体中的激发过程，不同激发参数对水体临界大小的影响进行了讨论分析.

1 有限水体内的气泡振荡模型及其有限元模拟

1.1 有限水体气泡振荡模型及控制方程

气枪在陆内水体中的激发问题可以近似为一个球形高压气泡在充满水的球形空腔中的振荡问题，空腔外是无限大的固体介质(图1).由于整个问题的球对称性，气泡和水体只存在径向运动.将复杂的气枪震源过程近似为一个球形高压气泡在水中的自由振荡问题是气枪和水下爆炸研究中的常规处理，与实际气枪实验数据具有很好的一致性(Ziolkowski, 1970, 1998; Johnson, 1994)，具体的近似包括(Ziolkowski, 1970)：(1)忽略重力，因为高压下气泡运动的加速度远大于重力加速度；(2)忽略水的黏性，因为黏性项的贡献远小于速度项的贡献(约百万分之一)；(3)忽略气泡的表面张力，因为其远小于高压气泡产生的压力.

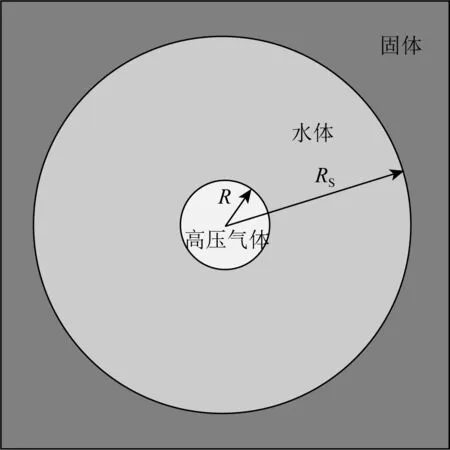
图1 有限水体内气枪激发模型R和RS分别是气泡半径和水体半径，其中R=R(t)是时间的函数，RS是常数.Fig.1 Air gun model in the finite water bodyR and RS are the radii of the air bubble and the water body, respectively. Of which R=R(t) is a function of time and RS is a constant.

水体运动的控制方程由动量守恒、质量守恒和介质状态方程组成.在拉格朗日描述下，无黏可压缩球对称水体的动量守恒方程为

(1)

其中ρ,u,p分别为水体的密度、速度和压力，t和r为时间和径向距离，D/Dt为物质导数.在拉格朗日描述下，坐标跟随物质点移动，因此任意指定区域内的质量不变(区域可能会变形)，

(2)

以下压力和密度的经验公式使这一关于ρ,u,p三个变量的方程组达到闭合 (Ziolkowski, 1970)，

(3)

其中p∞和ρ∞是无扰动状态下水体的压力和密度.n和B是经验参数，并沿用Ziolkowski(1970)选择：n=8,B=2500大气压.

气泡和固体的作用通过边界条件的形式施加于水体.气液边界处压力连续(忽略气泡的表面张力)，所以

(4)

其中R=R(t)是气泡半径，p0和R0是初始时刻的气泡压力和半径，γ=1.13为经验常数 (Ziolkowski, 1970).刚性固体边界的速度为零，因此，u|r=RS=0.

(5)

初始的气泡体积等于气枪容积，压力等于气枪枪压，水体无扰动状态的压力为气枪所在深度的静水压(大气压+ρg×气枪深度).

1.2 基于拉格朗日描述的显式有限元的数值实现

有限元方法首先使用形函数对速度等变量进行近似，然后求解控制方程对应的弱解.研究区域(从水体内边界到外边界)等分为N个单元，其中第i个单元对应从ri到ri+1的球壳，而ri=ri(t) 是第i个节点的位置.记ui,ai为节点i上的速度、加速度，其他位置上的值可由插值得到，

(6)

其中Ni(x)是第i个节点的权重函数，或称为形函数，取如下的线性格式：

(7)

压力和密度则定义在单元上，在每个单元内为常数 (Benson, 1992).

弱解并不要求处处满足动量方程，而是满足动量方程的某种加权积分，采用形函数作为权函数的方法称为伽辽金方法.使用伽辽金方法，动量方程(式(1))转化为

(8)

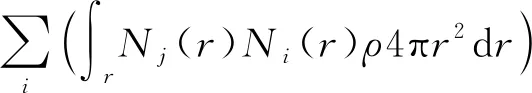
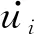
(9)

节点位置更新后，可以得到单元的新体积，进而根据单位质量守恒得到单元的密度.单元的压力根据状态方程(3)由计算得到，然后可以进行下一个时间步的计算.

1.3 数值模拟的参数选择

时间步长的选择由空间网格间隔和最快速度决定，过大的时间步长会导致数值模拟的不稳定.水中速度有两个：声波速度(1500 m·s-1)和激波速度.根据前人的研究结果，高压气泡产生的激波速度也约为1500 m·s-1(Liu et al., 2018b)，因此本文中采用min(Δr)/(4×1500)为时间步长，其中min(Δr)代表最小的空间网格，经验因子4是为了保证数值模拟的稳定.因为空间网格在模拟过程中会随着水体变形，所以时间步长在每个时间步后也会动态更新.

空间间隔通常由压力波场的最短波长决定，以保证对波场的准确描述.但激波的存在导致压力场存在间断，不能预先确定合适的最短波长.空间间隔为0.02 m到2 m的9个不同的实验结果表明Δr≤0.05 m的气泡振荡曲线没有明显区别(图2)，因此空间间隔选择为Δr=0.05 m.

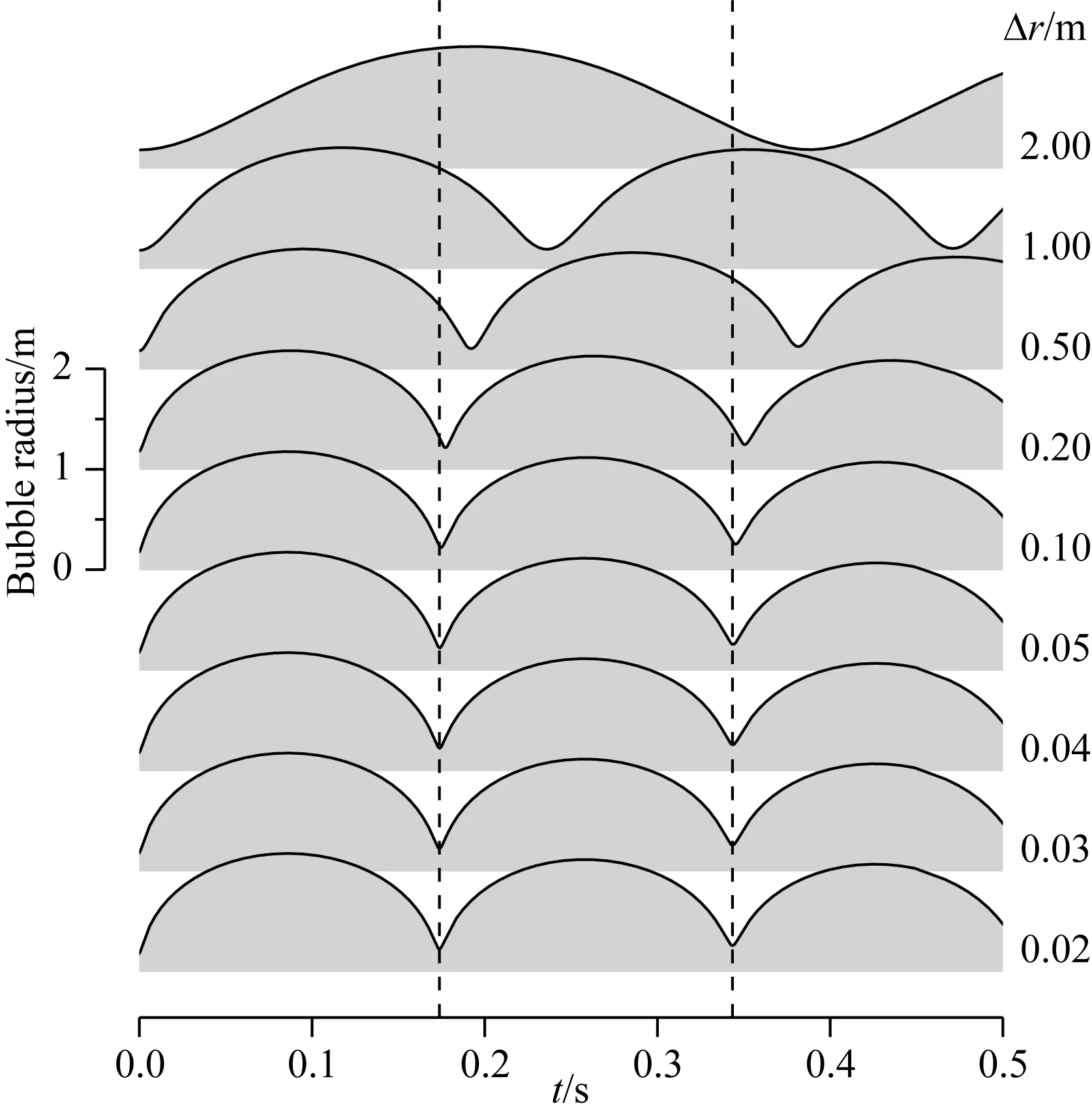
图2 空间间隔测试黑色实线为气泡半径随时间的变化曲线，2条黑色垂直虚线标注的是气泡收缩的时间(由Δr=0.02 m的气泡半径曲线确定)，空间间隔标注在右侧.该测试中使用的水体半径为300 m.Fig.2 Test of the node intervalBlack solid lines show the bubble radius as a function of time. The two black dashed lines mark the time of the bubble contraction, which is determined by the bubble radius obtained with Δr=0.02 m. The node interval is labelled on the right side. The radius of the water body used in the test are 300 m.

2 有限水体内高压气泡振荡的模拟结果

为了验证数值模拟结果的正确性，本文将大水体的有限水体气泡振荡曲线与无限水体的结果进行对比.采用的参数如下：气枪体积为1500 in3(0.02458 m3，1 in3=1.63871×10-5m3)，枪压为15 MPa，静水压以沉放深度为10 m计算，水体半径为300 m，模拟时长为0.5 s.按反射波的速度为1500 m·s-1计，两个模型在约0.4 s之前均为自由振荡，振荡过程应保持一致.无限水体的气泡振荡曲线使用Johnson(1994)的简化公式计算得到.两者对比表明，有限水体结果与无限水体结果的振荡周期和气泡大小在前两个振荡周期内具有较好的一致性(图3).两者之间的少许不同可能是由于Johnson模型的简化导致.

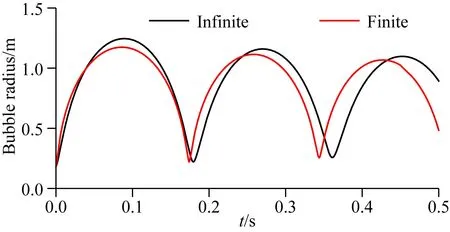
图3 与无限水体气枪模型的对比黑线为无限水体条件下气枪模型计算得到的气泡振荡曲线，红线为本文有限水体模型的计算结果.有限水体的水体半径为300 m，空间间隔为0.05 m.Fig.3 Comparison with the air gun model in infinite water bodiesThe black line is the bubble radius computed by the air gun model in an infinite water body. The red line is the bubble radius computed using our air gun model in a finite water body. The radius of the finite water body is 300 m. The node interval is set to 0.05 m.

为了研究有限水体效应作用于气泡振荡过程的影响，本文计算了14个算例，其中水体半径从10 m变化到500 m.气泡振荡曲线的对比表明，当水体半径大于300 m时，整个0.5 s长的气泡振荡曲线趋于一致，且与无限水体的结果一致(图4).水体半径为200 m时，气泡振荡曲线在第二个周期开始偏离大水体的结果.当水体半径小于100 m时，振荡曲线的第一个周期也开始偏离大水体的结果，并且振荡周期随水体半径减小而缩短.该结果证实了大水体中的气泡振荡曲线趋于无限水体的结果，而在小水体中出现明显偏离.

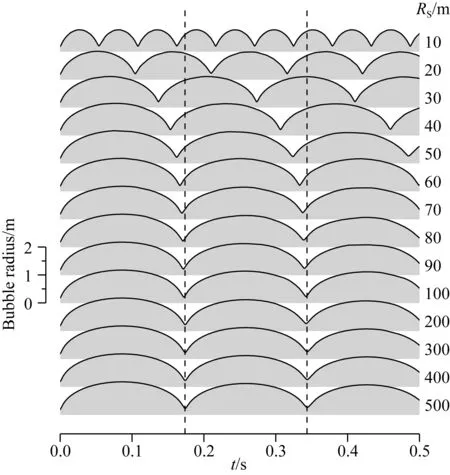
图4 不同大小水体中的气泡振荡曲线垂直虚线是RS=500 m对应的气泡收缩时间.Fig.4 Bubble radius in water bodies of different sizeVertical dashed lines are the time of bubble contraction corresponding to RS=500 m.

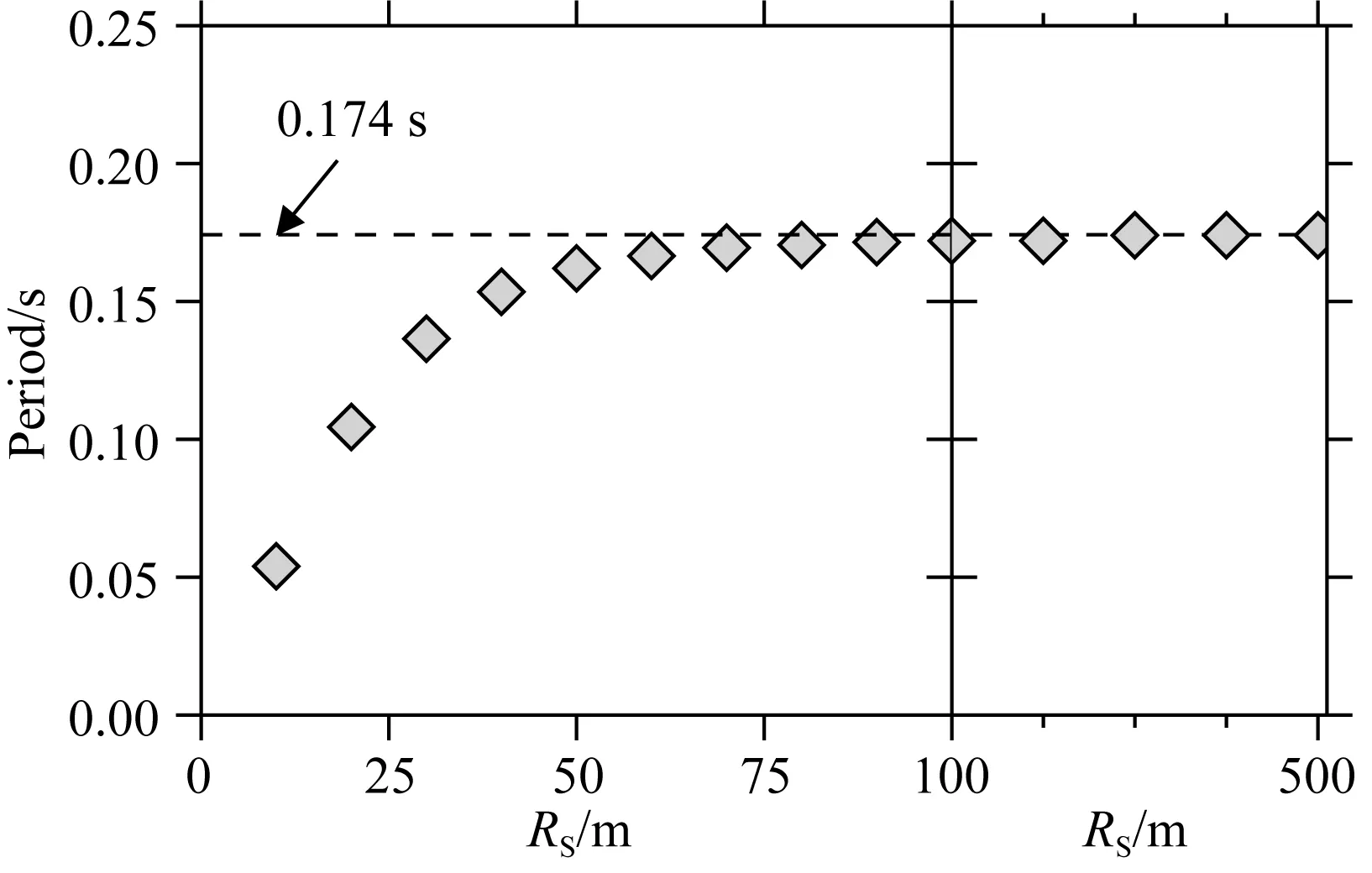
图5 气泡振荡周期和水体半径的关系黑色虚线为水体趋于无穷大时气泡振荡周期的极限.Fig.5 Period of bubble oscillation as a function of the radius of the water bodyThe black dashed line marks the limit of the period of bubble oscillation when the size of the water body approaches infinity.

使用两个气泡振荡的关键参数，气泡振荡周期(第一个振荡周期)和最大气泡半径，可以定量地确定有限水体效应的临界水体半径.振荡周期的结果表明，水体半径小于100 m时，振荡周期随着水体变大逐步增加，而半径大于100 m时，振荡周期稳定于0.17 s(图5).最大气泡半径呈现相似的趋势，水体半径小于60 m，气泡最大半径从0.78 m (RS=10 m)逐渐增加到1.17 m (RS=60 m)；水体半径大于60 m，气泡最大半径稳定在1.17 m(图6). 虽然两个关键参数得到的临界水体半径有些许不同(100 m和60 m)，不过均再次支持了小水体对气泡振荡过程存在明显的影响.

图6 气泡最大半径和水体半径的关系Fig.6 Maximum bubble radius as a function of the radius of the water body

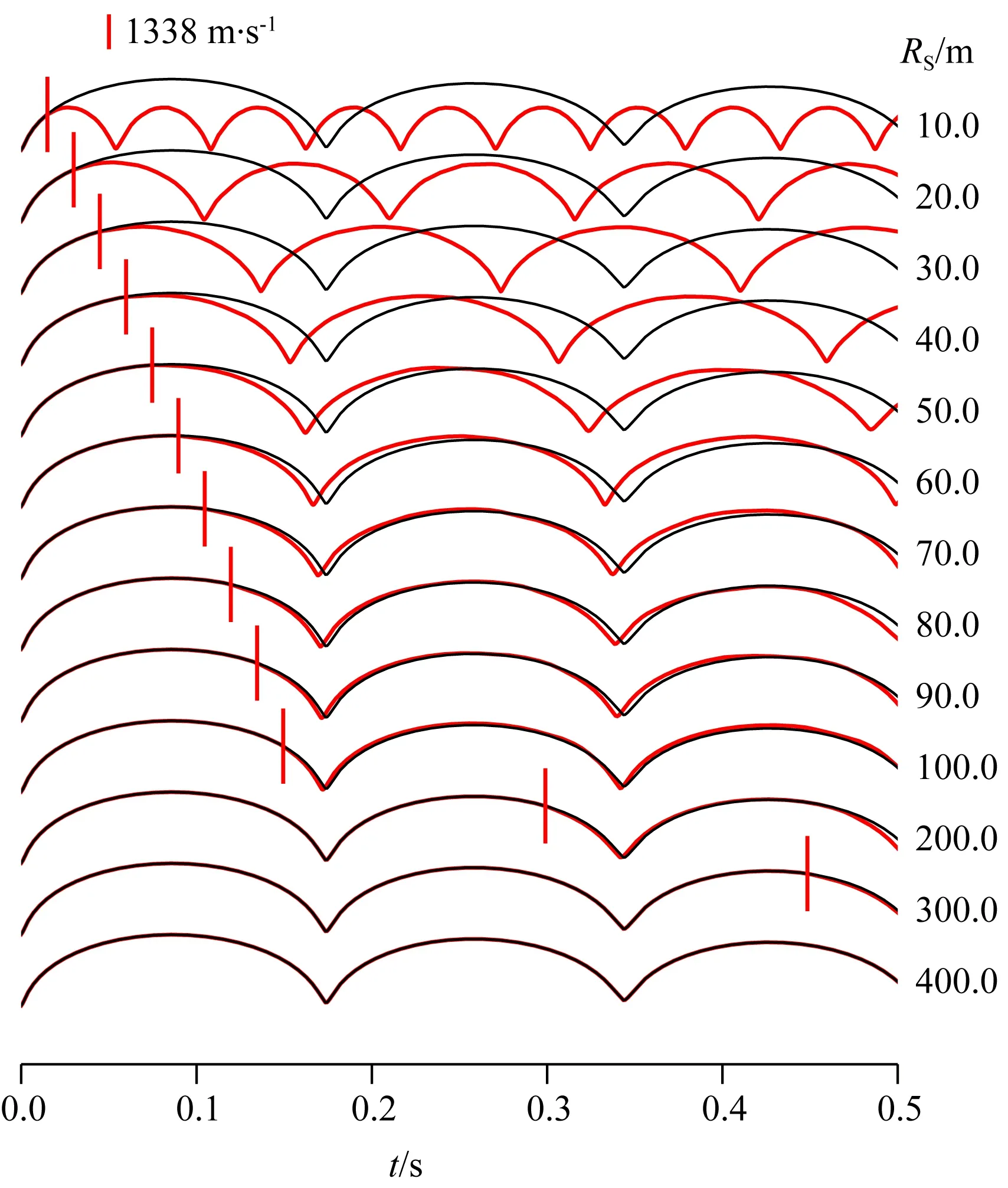
图7 有限水体气泡振荡曲线(红线)与“无限”水体(黑线)的对比“无限”水体的模拟结果由水体半径为500 m的有限水体模型得到，因为最快的反射波(0.667 s)在最大模拟时长(0.5 s)之后才会到达气泡壁.红色竖线标记了有限水体中的气泡振荡最早偏离“无限”水体曲线的时间，对应的速度为1338 m·s-1.Fig.7 Comparison of bubble oscillations in finite water bodies (red lines) to those in the ‘infinite’ water body (black lines)We used the finite water body simulation with the radius of 500 m as the result of ‘infinite’ water body.The fastest reflected waves arrive at the bubble at 0.667 s, later than our longest simulation time (0.5 s). The vertical red lines mark the earliest time when the bubble oscillations in finite water bodies deviate from the ‘infinite’ result, corresponding to the velocity of 1338 m·s-1.

气泡振荡曲线偏离自由振荡的时间可以提供理解有限水体效应的关键证据.以500 m水体的模拟结果作为参考(在前0.5 s处于自由振荡阶段)，10 m到400 m水体的结果的最初偏离时间与水体半径存在线性的关系，对应于速度为1338 m·s-1的应力波从气泡出发、经固液界面反射后返回到气泡的时间(图7).

水中压力场快照可以用来查看压力波的传播速度，进一步找到速度为1338 m·s-1的压力波的来源.半径300 m的水体的波场快照展示一个传播速度为1338 m·s-1的压力波(图8).这一压力波是气枪枪压和静水压之间的强压力间断产生的激波.虽然激波后续的波形存在明显的数值振荡，但其激波的前缘与1338 m·s-1的速度参考线吻合很好.

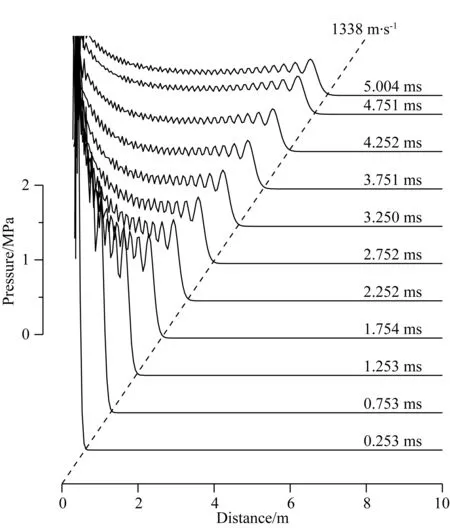
图8 压力波场快照.为了更好地显示激波，我们选择聚焦于10 m以内的压力场虚线是速度为1338 m·s-1的参考线.Fig.8 Snapshots of pressure wavefield. For better illustration of shock waves, we zoom in on the pressure field within the distance of 10 mThe dashed line is the reference line of velocity of 1338 m·s-1.

3 讨论

球对称有限水体气枪模型的有限元模拟表明，小水体和大水体的气泡振荡曲线存在系统性区别.不同尺度的水体中气泡振荡曲线在振荡初期具有很好的一致性，而后出现偏离，且偏离发生的时间与水体的半径存在线性关系.该线性关系对应的反射波速度与实验中激波速度吻合.气泡振荡周期和气泡最大半径表明，当水体半径小于60～100 m时，气泡振荡过程会与无限水体气枪模型存在较大的差别.当水体半径大于100 m时，气泡振荡过程与无限水体模型比较接近，这时使用无限水体模型计算震源子波不会有明显的误差.

3.1 气枪在陆内水体的激发过程及其在海洋中激发的区别

气枪在海洋和陆内水体中的过程具有一定区别，对其进行对比利于理解陆内水体的气枪激发模型.本质而言，气枪在海洋和陆内水体的激发过程具有很高的相似性：先在气枪内充入高压空气，然后在水中释放.释放时气枪内外有几十到几百大气压的压力差，高压力差会激发在水中传播的压力间断——激波，产生主压力脉冲(Liu et al., 2018a).气泡两侧的压力差还会将水体推离气枪所在位置，导致高压空气泡的膨胀及其压力降低.当气泡内外压力相等时，水体会由于惯性的原因继续往外移动，但负压力差会降低气泡扩张的速度，直到气泡扩张速度降为零，此时气泡膨胀到最大.随后，气泡由于负压力差开始收缩，经过气泡内外压力相等的位置时，会同样由于惯性的原因继续收缩，但收缩速度会开始减慢.当气泡收缩到最小时，气泡压力差为正，然后开始新一轮的膨胀过程.这种周期性的气泡膨胀收缩过程会产生压力波.这些压力波会穿过水底和岸边转换为地震波，同时也有部分压力波的能量会在水面和固液边界之间发生反射或多次反射后再转换为地震波.

海洋勘探中，往往利用的是气枪高压气体释放时产生的高频信号，用来提高勘探的分辨率.而在陆内水体激发时，为了实现更远距离的探测，所分析的信号为气泡振荡产生的相对低频的信号.就气泡振荡而言，海洋和陆内水体气枪的主要区别在于气枪离固液边界的距离.海水深度为几百米到几公里，而陆内水体的深度通常为十几到几十米.由于气枪信号的振幅衰减与传播距离呈正相关，小水体意味着反射波的振幅更强，更可能对气泡振荡本身产生影响.

反射波影响气泡振荡的原理是反射波到达气泡壁时会改变气泡内外的压力差，进而改变气泡振荡的过程.如图9所示，当反射激波(压力间断)到达气泡壁时，会迅速增加气泡壁上的压力，在短时间内(10 ms)形成负加速度(图9b)，降低气泡膨胀的速度，使得气泡振荡过程偏离了自由振荡(图9a).虽然之后的二次反射(到时约0.014 s)又短暂提高了速度，但已无法将气泡膨胀的过程校正回原本的程度.

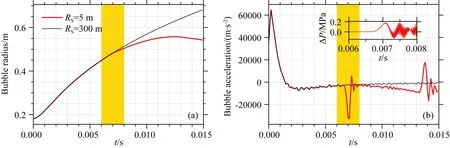
图9 反射激波到达气泡壁时气泡半径、加速度和气泡外壁上的压力(a) 气泡半径； (b) 气泡加速度，内嵌图展示的是水体半径为5 m和300 m的气泡壁上的压力差.作为参考的水体半径为300 m的结果在前0.015 s仍处于自由振荡阶段.黄色区域显示的是反射激波到达气泡壁的阶段.Fig.9 Bubble radius, acceleration and pressure on the bubble wall when shock wave reflected to the bubble(a) Bubble radius; (b) Bubble acceleration. The inset map shows the difference in pressure on the bubble wall between the radius of the water body of 5 m and 300 m. The result with RS=300 m is still in undisturbed bubble oscillation within the first 0.015 s. The yellow region highlights the period when the reflected shock wave arrives the bubble.

3.2 气枪激发参数的影响

气枪的枪容、枪压和沉放深度是气枪激发的重要参数，三者决定了无限水体内气泡振荡过程，也在有限水体模型中起着重要作用.

改变枪容、枪压和沉放深度对气泡振荡周期产生了明显的影响(图10).当水体较大时，单独将枪容从1500 in3增加到8000 in3会导致气泡振荡的周期从0.174 s增加到了0.3035 s，降低枪压(15 MPa到7 MPa)会减小振荡周期到0.1355 s，增加沉放深度会减小振荡周期到0.1445 s，因此气泡振荡周期的改变与气枪的枪容、枪压呈正相关，与沉放深度呈负相关，换言之，如果想要降低气枪信号的气泡振荡阶段的主频(低频信号衰减更慢，探测距离更远)，可以采用增加枪容(或者采用多枪同时激发)、增加枪压、或者减小沉放深度的方法.这三种方法的一致作用是导致气泡最大半径的增加，因此可以简单地理解为大气泡的振荡周期长，小气泡的振荡周期短.

气枪释放能量的公式为(Ronen, 2002; 陈颙等, 2007b)

(10)

其中P是枪压，V是枪容，P0是静水压力(主要由沉放深度决定).该公式表明，导致气泡最大半径增加的参数改变也会增加气枪能量，因此水体半径较大时，气泡振荡周期、气泡最大半径和气枪释放能量三者呈正相关.

当水体半径很小时(<20 m)，改变这三个参数对于气泡振荡周期的影响很小(图10).可能意味着在这个水体尺度下，有限水体效应已经占据了主导作用，改变气枪本身的激发参数已较难控制气枪激发频率.

其次，仔细观测曲线的变化可以发现，大气泡的临界水体半径比小气泡的更大，意味着在同等尺度的水体中，大气泡受到的有限水体效应更明显.

3.3 理论模型与陆内水体气枪实验的对比分析

在已经开展的陆内水体气枪实验中，在不同大小的水体中均开展了气枪激发，并在近场记录了震源信号.将有限水体模型模拟结果与实测结果进行对比，可以验证相关结果的可靠性.

在云南宾川大银甸人工水井中的实验是典型的小水体：水井半径2.5 m，井深20 m.气枪沉放深度为12 m，距离水体边界的垂向和横向距离分别是8 m和2.5 m，平均距离约为5 m(胡久鹏等，2017).根据图5中展示的振荡周期曲线的趋势，对应的周期约在0.2～0.3 s, 即33～50 Hz，与实测气枪信号的气泡振荡主频(约35 Hz)有很好的一致性(胡久鹏等，2017).这说明在小尺度的陆内水体中，需要考虑有限水体效应，且本文的有限水体模型可以很好地估计气泡振荡的频率.

另一个小水体的例子是北京昌平开展的马刨泉实验(Wang et al., 2010).马刨泉是一个水面直径为25～37 m的人工水池，气枪沉放深度为11 m，沉放处的水深为14.5 m.气枪与水体边界的垂向(到水底)和横向(到岸边)距离约为3.5 m和15 m，取其平均约为10 m.根据图5中展示的振荡周期的曲线，水体半径为10 m的球对称有限水体气枪信号的振荡周期约为0.05 s，即20 Hz，与实测的主频(20～25 Hz)具有很好的一致性(Wang et al., 2010).

新疆呼图壁人工水池是一个轴对称的碗形水体，水面半径为48.5 m，深15 m(魏斌等，2016).气枪位于水体中心，距岸边约48.5 m，距水底5 m，平均距离约25 m，对应的振荡频率为6.6 Hz.实测气枪信号由高频(40～50 Hz)的主脉冲和低频(约3 Hz)的气泡振荡组成(胡久鹏等，2017)，理论预测的频率低了一半.可能的解释是呼图壁实验使用了6条气枪，气泡能量更大，导致振荡周期降低.

宾川大银甸水库水面直径更大(约1 km)，但由于水面形状不规则，且气枪不在水库中心(离岸边30 m处)，气枪距离水体边界最近为3 m(水底)，离岸边最近为 30 m，最远距离为1200 m，情况更为复杂.实测的气枪信号中有多个频率，分别为5，10，20，40 Hz，与有限水体模型预测的振荡周期对比(图10a)，分别对应于水体半径为40，20，10，5 m.可能的解释是：(1)气枪离水体边界的距离变化产生多个振荡周期；(2)最低的振荡周期与水体自由振荡有关，而更高频的信号由主脉冲或谐振产生.进一步检验具体原因可能需要对非规则的水体中的高压气泡振荡问题进行数值模拟.

3.4 未来可能的改进

本文描述的数值模拟方法虽然可以很好地研究有限水体对气枪振荡过程的影响，但激波后存在明显的数值振荡(图8)，可以通过增加数值黏性来解决 (von Neumann and Richtmyer, 1950; Brode, 1955; Persson and Peraire, 2006).此外，将固体介质从刚体改为弹性体，应该可以更准确地模拟气泡的振幅，并给出准确的震源子波.这两个改进可以在球对称的框架下进行.

非规则水体对气泡振荡的影响不能继续使用球对称框架，需要在二维或三维条件下求解水体的控制方程.该情况下将网格依附在气泡边界上的做法可能较为复杂，更可行的方法是将气泡、水体、固体都包括在计算域中，利用Level set或Volume of Fluid method (VOF)等方法来描述边界(King, 2016; Liu et al., 2018b).

目前气枪模型中主脉冲被简化为高压气泡的初始压力、体积和速度.为了更好地描述主脉冲，可以采用数值模拟方法对气枪枪体和气阀建模，模拟高压气体喷射出枪体形成高压气泡(或者泡沫流)的过程.这一研究可能需要比气泡振荡模拟更密的空间网格，可以单独模拟后作为初始条件加入到有限水体气枪模型中.

4 结论

充液球腔的球对称有限水体模型可以较好地解决陆内水体气枪的关键参数：无限水体模型失效的临界水体大小.使用球坐标系下的一维显式有限元方法的数值模拟结果表明，临界水体大小约为100 m.气枪在小于这个尺度的水体中激发时，会受到固液边界反射激波的影响而偏离自由振荡过程.临界水体大小受到初始枪压、枪容和沉放深度等因素的影响，与枪压、枪容呈正相关，与沉放深度呈负相关，且三者可统一为与气枪能量呈正相关.有限水体气枪模型可以帮助理解陆地小水体对气枪震源激发过程的影响，定量地衡量有限水体效应.未来可以在该模型的基础上考虑更复杂的情况，比如气泡在非规则水体中的振荡过程.

致谢谨此祝贺陈颙先生从事地球物理教学科研工作60周年．