基于MA-SVM方法的短期光伏功率预测

徐 萌

(国能智深控制技术有限公司，北京 102211)

0 引 言

太阳能具有间歇性、不确定性等特点，并受多种气象环境因素影响。为了实现光伏发电的大规模并网，应对其发电功率变化趋势做出较为准确的预测。综合考虑多方面因素，减少光伏发电预测各关键环节的误差，提高预测的精准度，增强光伏发电的可控性是当前新能源发电领域所面临的重要挑战之一。

光伏发电功率预测按照预测的时间长度可分为中长期预测、短期预测、超短期预测，分别预测1个月～1年、4小时～3天和数分钟～4 h的光伏功率[1]。其中，光伏发电功率短期预测的时间尺度对于电网调度具有重要的实际意义，且能达到较高的预测准确度。因此，光伏发电功率短期预测的研究成为新能源发电研究的热点之一。

光伏发电输出功率的预测方法分为物理方法、统计方法及综合方法。其中多数研究采用的是统计方法或者以统计方法为主的综合方法。文献[2]提出了一种结合深度信念网络(DBN)与Takagi-Sugen(T-S)模糊时变权重组合的光伏功率方法，利用DBN模型弥补了T-S模糊筛选输入变量时带来的精度损失问题，利用遗传算法(GA)赋予时变权重，提高了超短期预测准确性，不适用于短期功率预测。文献[3]利用最小二乘滤波识别时间序列数据中的突变，建立了基于最小二乘滤波-肖维勒准则的光伏功率异常数据识别模型，剔除异常数据并提高训练模型的准确度，但对于气象因素导致的规律性数据缺失较为敏感。文献[4]提出了相似日理论和一种结合纵横交叉算法与改进的高斯过程回归算法(CSO-WGPR)，通过聚类的方法，构建相似日集合，再采用改进的高斯过程回归模型减小异常数据对预测结果的影响，但对于非典型气象预测日效果相对较差。文献[5]提出了一种季节自回归积分滑动平均(SARIMA)方法与支持向量机(SVM)方法结合的预测思路，并用于一个20 kW的光伏发电站实际预测中，2种算法均针对光伏功率数据展开，并未解决预测日气象数据获取滞后的问题。文献[6]提出一种基于经验小波变换和粒子群算法的组合预测方法，将利用灰色关联分析聚合的相似日集合分解为高、中、低不同的频率子模态，该方法对超短期预测具备可行性与实用性，但不适合短期预测的要求。文献[7]介绍了一种基于奇异谱分析(SSA)和K均值的时延特性-反向传播(TD-BP)神经网络超短期光伏功率预测方法，通过SSA的分解及重构，提取时间序列中的趋势，并利用K均值聚类法将天气样本聚类，该方法同样为超短期预测而设计，不适合短期功率预测。文献[8]使用小波降噪的方法处理光伏功率的历史曲线，并使用灰色关联分析方法筛选强相关的气象条件因素，建立基于双向长短期记忆网络(BLSTM)与随机森林的短期光伏发电功率预测模型，得到了较好的预测效果，但存在与文献[5]类似的气象数据预测的问题。文献[9]采用改进麻雀搜索算法与SVM方法预测短期的光伏发电功率，采用自适应t分布增强麻雀搜索算法的种群多样性，提高了预测的准确度，但该方法的季节特性明显，针对秋冬季的效果明显优于春夏季。文献[10]提出一种结合灰色关联分析和GeoMAN模型的光伏发电功率短期预测方法，利用解码器提取输入变量的时间特性，融合晴空指数和数值天气预报实现功率预测，该方法要求被预测地区具有多个光伏电站以供空间相关性分析，对被预测的对象要求较高。文献[11]提出了基于改进果蝇算法的太阳辐照度预测方法，能够检测出太阳能照度光线实值且发现长度更大，可与光伏发电功率预测相结合。文献[12]设计了基于粒子群优化-反向(PSO-BP)神经网络的光伏功率预测方法，针对BP神经网络模型收敛慢、易陷入局部最优值的问题，配合PSO方法优化初始参数。同时，在预测方法理论方面，文献[13-16]也对预测方法和应用进行了研究。

为解决预测目标日的气象数据获取滞后的问题，本文利用相关性分析法选择与光伏功率相关的气象数据种类，用时间序列方法预测电站所在区域的气象数据，得到光伏发电现场更为准确的气息信息预测值，并利用改进的SVM算法对光伏功率预测建模。

1 研究方法

在光伏发电的各个影响因素中，辐照度是最为重要的因素[17]。辐照度包括总辐照度、直射辐照度、散射辐照度等。除此之外，温度、湿度等气象因素也与光伏发电功率相关。本文采用时间序列方法，对预测范围内的气象信息进行预测，获得所求区间的气象信息数值，避免天气预报对光伏电站所在的具体位置的预报不准确。然后釆用SVM方法对气象信息和光伏输出功率的关系建模，代入所求区间的气象数据预测值，即可得到所求区间光伏功率的预测值。

1.1 气象条件相关性分析

为了降低输入数据的维度，减少无关变量或低相关度变量对预测结果的干扰，在选取SVM的输入数据时，采用相关性分析的方法，筛选与光伏功率强相关的气象信息变量。常用的分析手段包括相关性分析法、主成分分析法等。

光伏电站及其配套的气象信息检测平台在运行过程中不断积累数据，通过对其挖掘分析，能够归纳各个气象参数与光伏输出功率的相关性，进而利用主成分分析将众多的输入变量整合成少数几个主成分变量，更清楚地观察到各个气象参数作用于光伏输出功率的途径[18]。

1.1.1 相关性分析

通过相关性分析能够衡量2个变量间的线性相关程度，以皮尔逊相关系数为例，其定义为2个变量的协方差除以2个变量的标准差的商，即：

ρX,Y=corr(X,Y)=

(1)

且有：

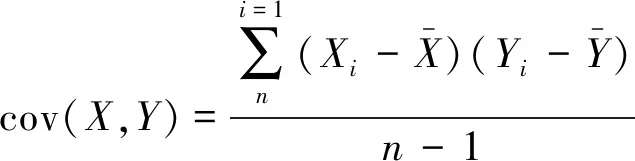
(2)

根据数学定义可知，其取值在-1～1之间，且数值越大表示相关性越强。

1.1.2 主成分分析

各种气象参数之间存在互相的关联，其作用于光伏功率输出的路径不是独立的。借助主成分分析，能够将冗余的气象信息转化为一组线性无关的组合变量，实现数据的降维。与光伏功率相关的气象因素包括辐照度(总辐照度、直射辐照度、散射辐照度)、温湿度(环境与光伏组件)、露点、风速(瞬时风速、平均风速)、透光率和反射率等。

对于上述光伏功率相关的气象参数，基于参考电站长时间运行产生的大量数据，可获得主成分的划分。主成分划分的一种方法是将上述气象参数分为辐照度分量和温湿度分量等，并获得每个分量中每种气象信息的组合关系。

1.2 时间序列方法

时间序列的数据挖掘方法包括指数平滑法(ES)，又可进一步详细分为一次、二次、三次指数平滑法[19]。该方法可以理解为一种特殊的加权平均法，按照离目标点越近的数据权重越大的原则，将气象信息按指数递减的规律分配权重，越接近预测目标的数据权重越大，反之权重越小。

三次指数平滑法对非线性变化的气象信息数据具有较好的预测效果，第t+T分钟的太阳辐照度预测值为

Yt+T=at+btT+ctT2

(3)

式中:T为预测周期；Yt+T为基准时间第t分钟，预测周期T分钟的太阳辐照度预测值；at,bt,ct均为平滑系数。

其中平滑系数为

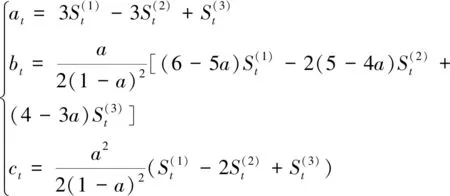
(4)

利用时间序列方法中的三次指数平滑法，可由目标日前几日的辐照度、温度等气象信息得到目标日的所需气象信息。

时间序列法常用于对光伏功率数据的直接处理，而非预测气象数据。先对气象数据的先行预测为光伏功率的预测提供了输入。同时,与该地区的气象预报相比，时间序列方法更能够对应光伏电站现场的气象条件，提高预测的准确度，解决预测目标日气象数据获取滞后的问题。

1.3 支持向量机方法

支持向量机是一种二分类模型，是定义在特征空间上的间隔最大的线性分类器，根据结构风险最小化准则,对于高维非线性样本具有较好的效果。支持向量机将计算过程转化为一个二次型寻优的问题，一定程度上避免了神经网络算法容易陷入局部最小值的问题[20]。

支持向量机的思想基于统计学习理论，通过建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘最大化,近似实现结构风险最小化。具有通用性高、鲁棒性好及简单有效等优点。核函数是支持向量机理论的关键，包括线性核函数、多项式核函数、两层感知器核函数等等多种形式。

支持向量机的优化问题可转化为调整参数使式(5)最小的问题[21]：

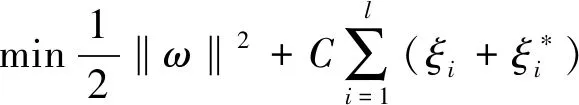
(5)

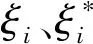
需要满足的约束条件如下：

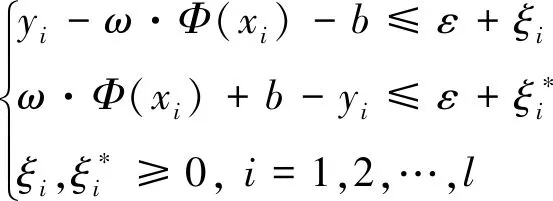
(6)

式中:b为阈值；Φ(x)为从输入空间到高维空间的非线性映射。

上述问题可转化为最大化二次型求解问题，即：

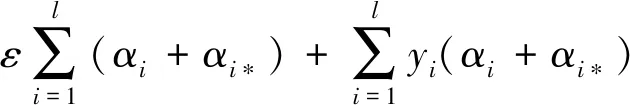
(7)

需要满足：

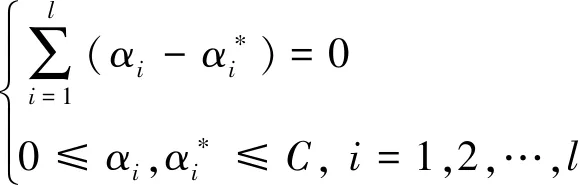
(8)

综上，回归方程可表示为

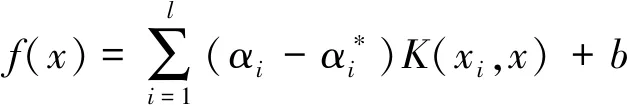
(9)

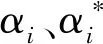
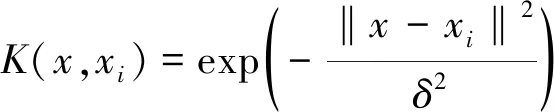
(10)

式中:K为核函数;δ为核函数宽度。

以辐照度、温度、湿度等气象信息作为输入，光伏功率作为输出，训练SVM模型。再将利用三次指数平滑法预测到的目标日辐照度、温度等气象数据作为输入，可由SVM模型得到输出，也即目标日的预测功率。

2 预测模型构建

目前，我国的太阳辐照度检测的站点比较少，使得很多论文研究数据源只能选择距离较近的光伏发电站和气象信息检测站，这无疑为试验结果带来了误差，且目前也没有类似温度预报的、较完善的辐照度预报系统。因此，很多研究只能以辐照度的真实值代替预报值来进行光伏功率的预测。这样的研究方法虽然准确性比较高，但存在不能用于实践的问题。

针对上述问题，本研究构建了一套光伏发电系统以及配套的能够检测环境因素，包括太阳总辐照度、散射辐照度、温湿度等多种气象信息的气象监测站。2套系统彼此配合，测得的气象数据与光伏发电功率数据彼此对应性好。试验系统如图1所示，测量仪器的类型及特性如表1所示。

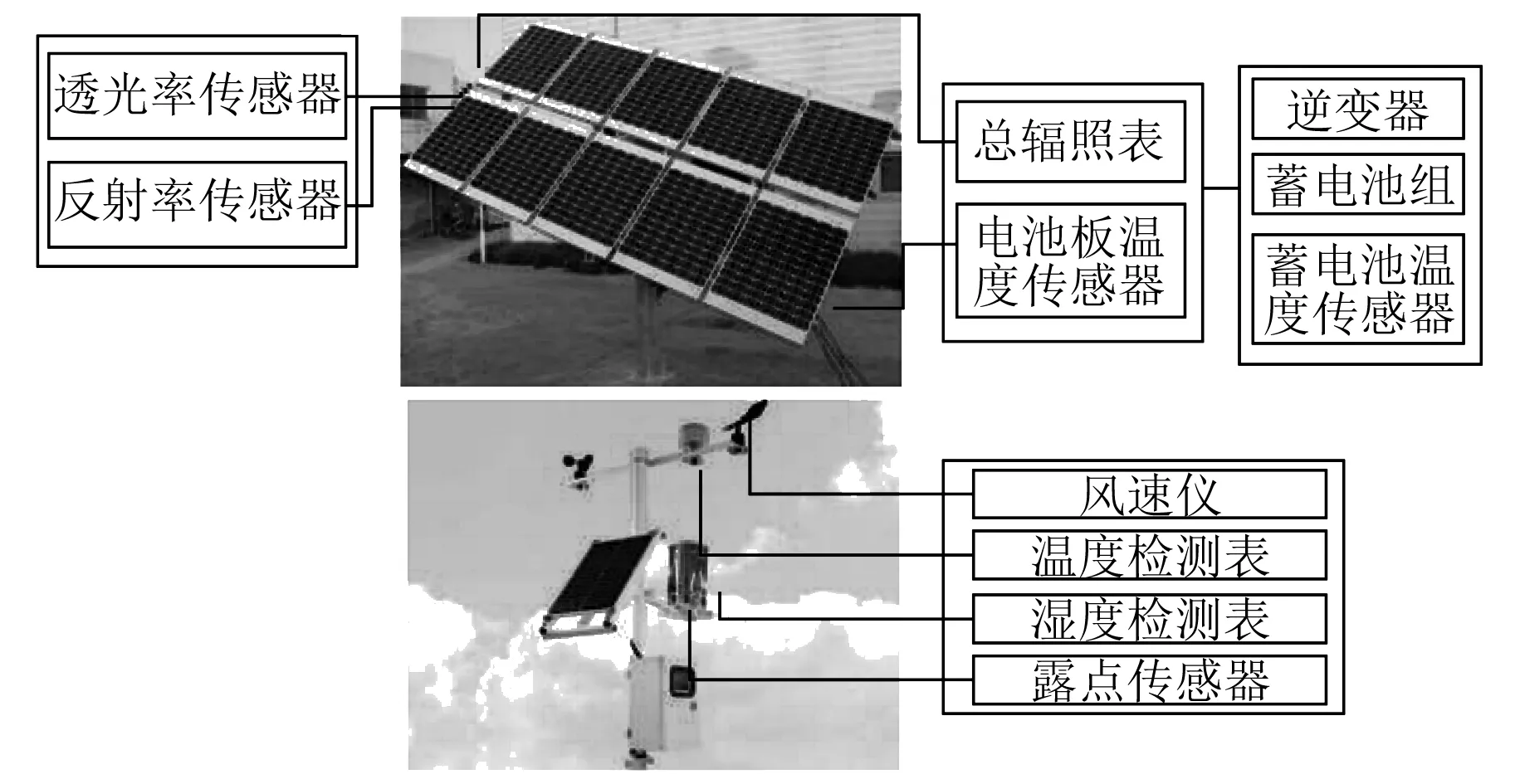
图1 气象信息监测站及光伏发电试验平台

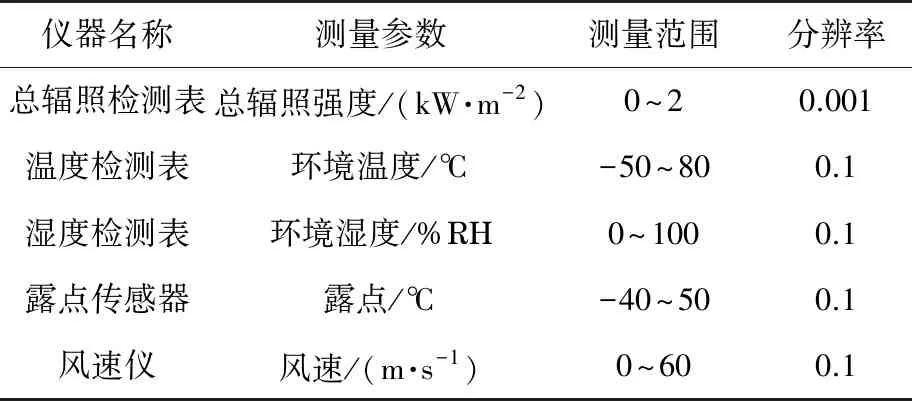
表1 试验平台测量仪表及参数

结合上述方法与实际情况，可构建基于MA-SVM模型的光伏功率预测方法。结合历史数据库中各时刻的气象数据与光伏功率的关系训练支持向量机回归模型，再利用时间序列方法预测出目标日的气象信息，代入支持向量机回归模型，可预测得到目标日的光伏功率预测值。结合时间序列预测方法、支持向量机回归方法的优势和特点，建立如图2所示的预测过程。

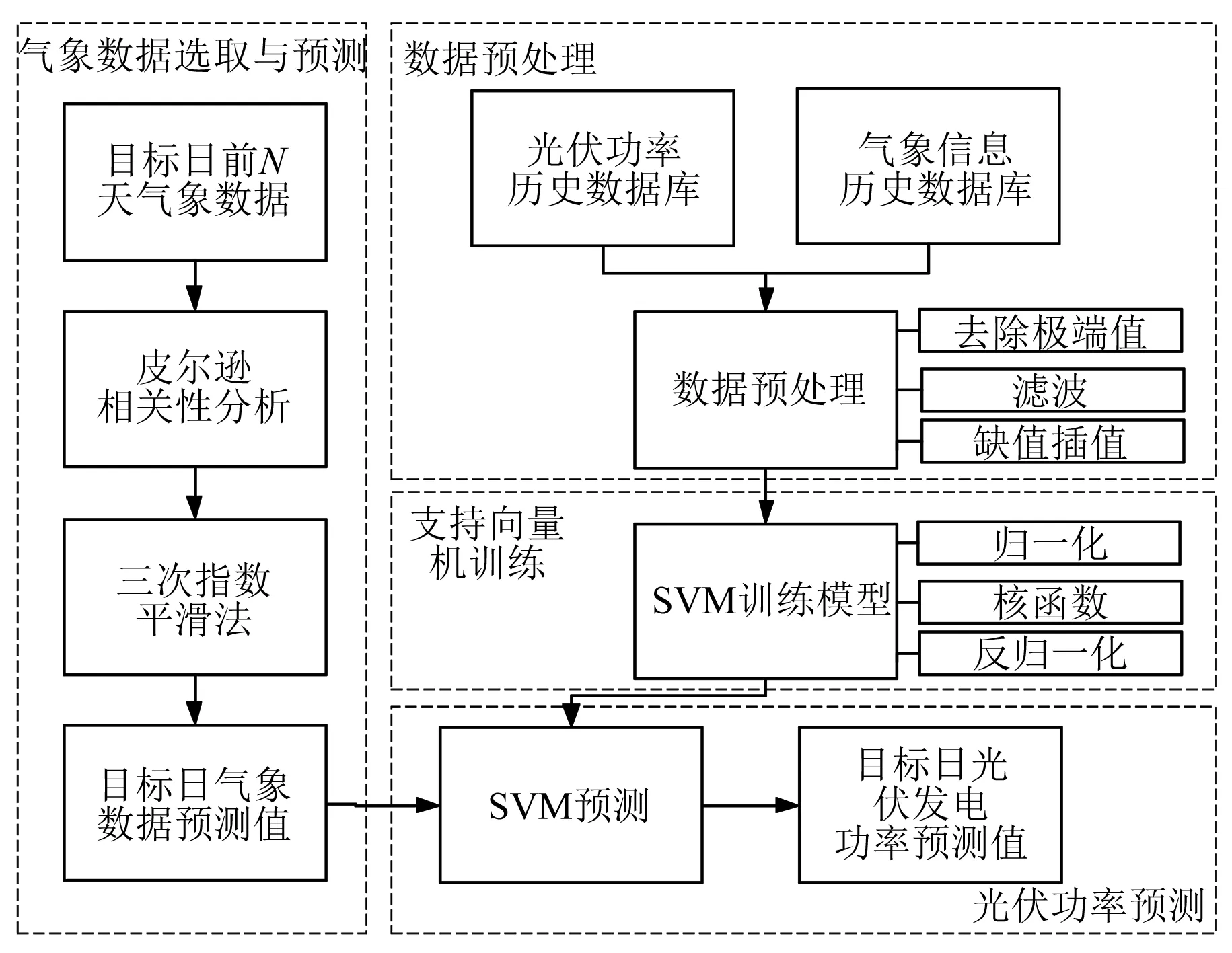
图2 基于时间序列和支持向量机方法的光伏功率预测流程图

3 实例分析

选取2021年10月8日为目标日，总体较为晴朗，符合常见的晴天模型，详细的气象数据如表2所示。

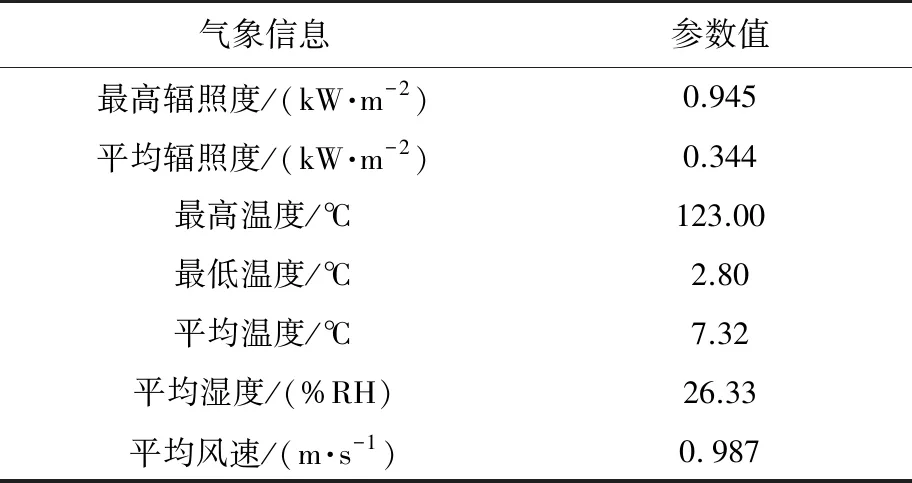
表2 目标日的气象条件分析

目标日气象发电条件在上午10点左右达到峰值，之后逐渐稳定，在14点左右发电条件下降，光伏功率随之降低。

其气象参数变化趋势如图3所示。其中图3(a)～图3(c)分别表示风速、辐照度、湿度的变化趋势。

3.1 相关性分析和主成分分析

定义气象参数并经计算，气象信息与光伏功率的相关性如表3所示。

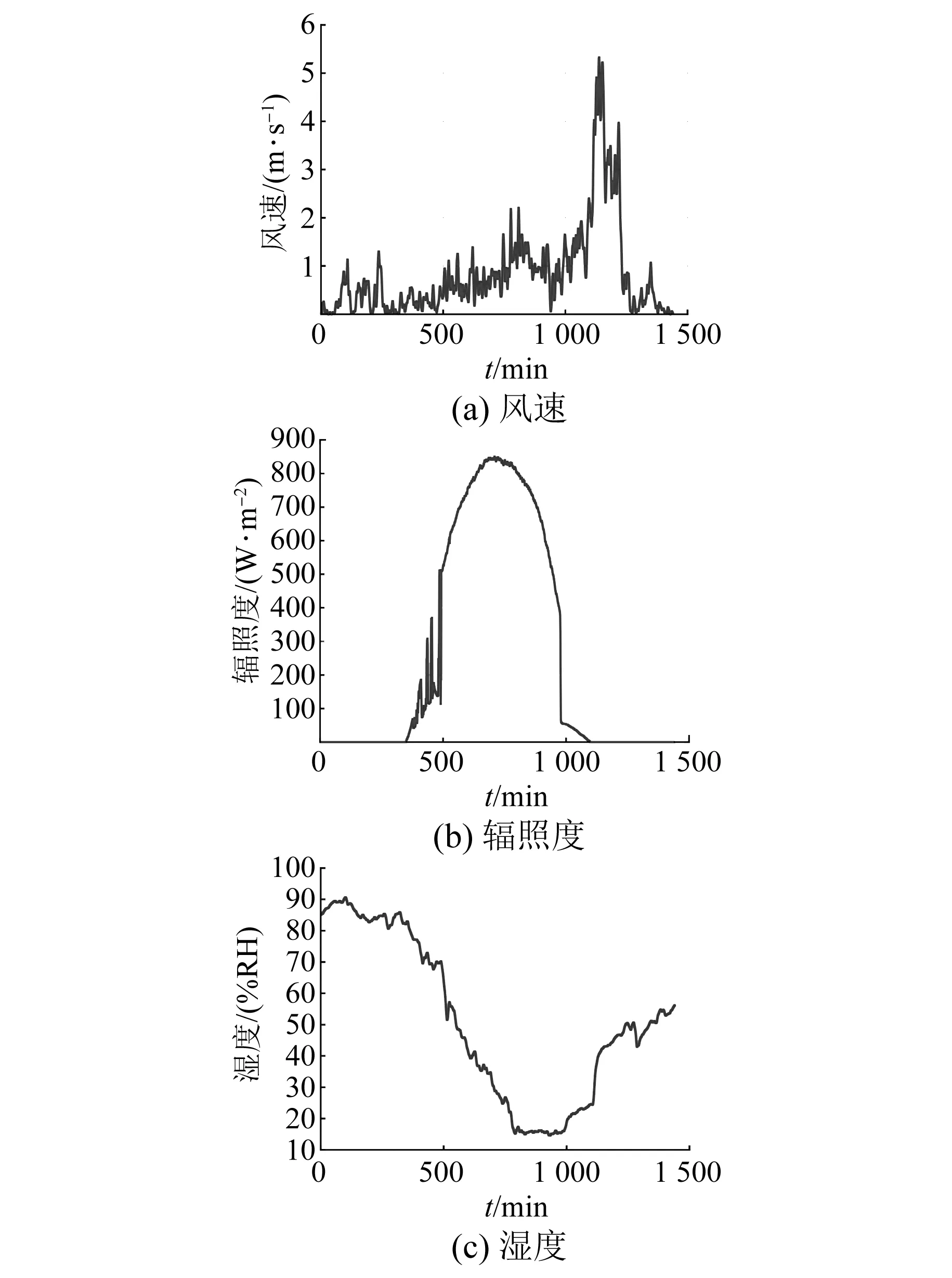
图3 目标日气象信息变化趋势图

表3 气象信息与光伏功率相关性

在主成分分析中，选取特征根大于1的成分作为主成分。经计算，其表达式分别为

F1=0.032X1-0.067X2-0.135X3+0.478X4+0.349X5+0.215X6+0.032X7+0.104X8+0.032X9+0.023X10+0.076X11

(11)

F2=0.223X1+0.557X2+0.401X3-0.043X4-0.109X5+0.252X6-0.057X7+0.224X8+0.078X9+0.042X10-0.057X11

(12)

F3=0.026X1-0.105X2+0.034X3+0.107X4+0.134X5+0.107X6-0.126X7+0.301X8+0.345X9+0.062X10+0.008X11

(13)

F4=-0.143X1-0.032X2+0.028X3-0.073X4+0.124X5-0.137X6+0.353X7+0.331X8+0.001X9+0.365X10+0.489X11

(14)

根据每个表达式中占据主要成分的变量，可对其分类如下：

F1中占据主要成分的是各种辐照度(总辐照度、散射辐照度、直射辐照度)，即主要表达辐照度对光伏发电功率的影响。

F2中占据主要成分的是露点、湿度因素，因此该主成分反映了湿度相关因素对光伏发电功率的影响作用。

F3中占据主要成分的是组件温度、环境温度等因素，因此该主成分主要反映了温度对光伏发电功率的影响。同时也能看出温度而辐照度二者的相关性。

F4中占据主成分的是其他因素(反射率、透光率、平均风速、瞬间风速等)。

3.2 目标日气象信息预测

对2021年10月1日～10月7日的辐照度、温度等气象数据预处理，去除极端值并标准化后，利用三次平滑算法，对气象信息进行时间序列预测，得到目标日的气象数据，这将作为SVM模型的预测输入值。

3.3 光伏功率预测

3.3.1 模型建立及参数选择

构建基于支持向量机模型的回归模型是预测光伏发电功率的基础。每组数据包括输入数据及其对应时刻的输出数据，各组数据组合形成数据矩阵，再对其标准化。输入数据为气象信息数据，具体包括辐照度、温湿度、环境风速等信息，输出数据为光伏功率。输入输出数据保持时间上的一致，每一分钟设置一个采样点。

选择K-Fold Cross Validation的交叉验证方法，将训练数据集分组，并对惩罚参数c与核函数参数g进行选择。经过计算，c和g分别取0.342 77和2.218 87。

3.3.2 回归拟合

基于参数c与g构建支持向量机模型，经过训练拟合，效果如图4所示。可见训练得到了良好的拟合效果。

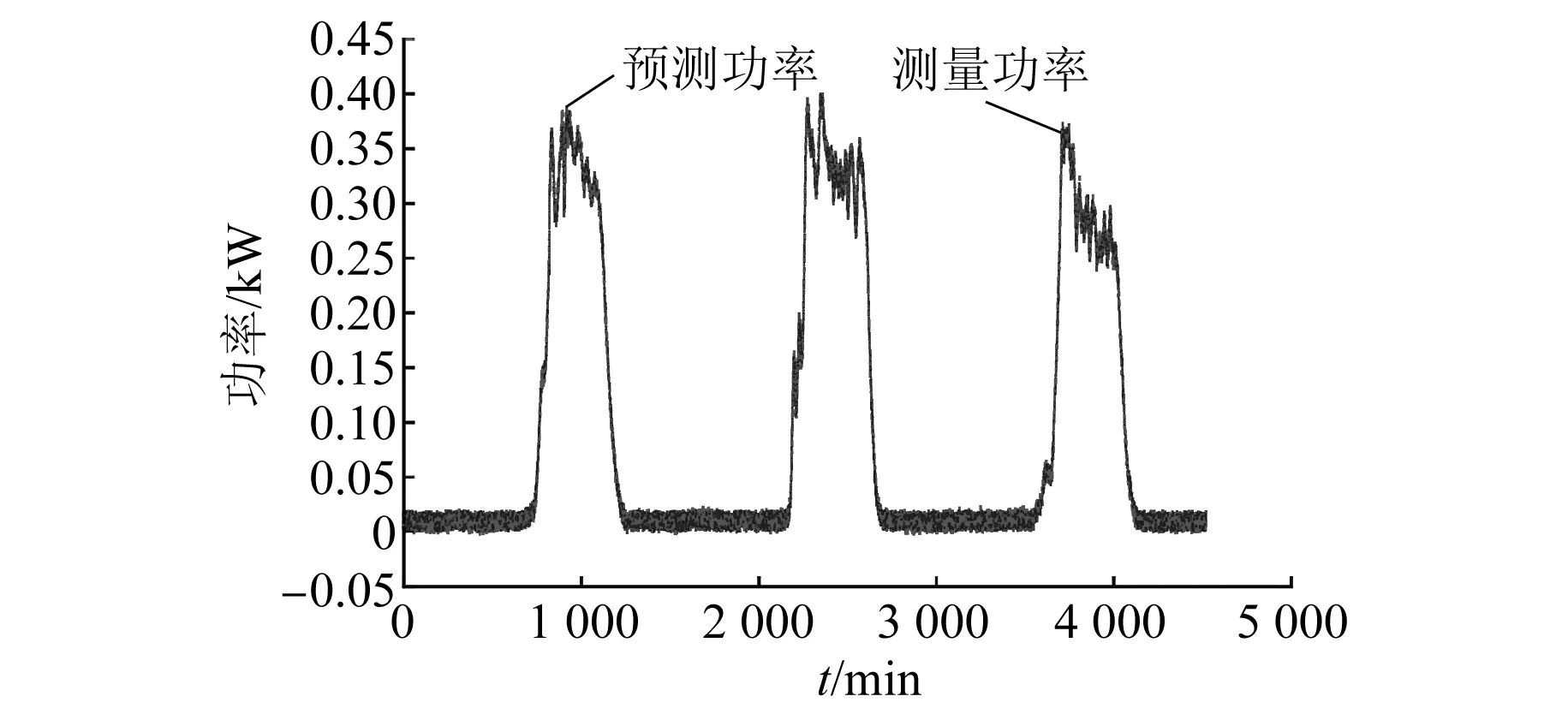
图4 回归分析中拟合效果图

经过拟合过程即得到训练后的模型，可用于光伏功率的预测。按照前文所述过程进行预测，并对预测误差进行如下分析。

3.4 结果与误差分析

可采用均方根误差(RMSE)作为衡量误差的评价指标，其定义如下：

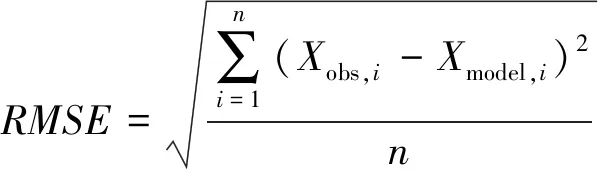
(15)

式中：n为变量个数；Xobs,i和Xmodel,i分别为实际值和预测值。

预测过程主要包括2个阶段，即气象信息预测阶段和支持向量机预测阶段，分别进行误差的分析。

以露点和温度为例，气象信息预测阶段的预测效果和误差如图5所示。

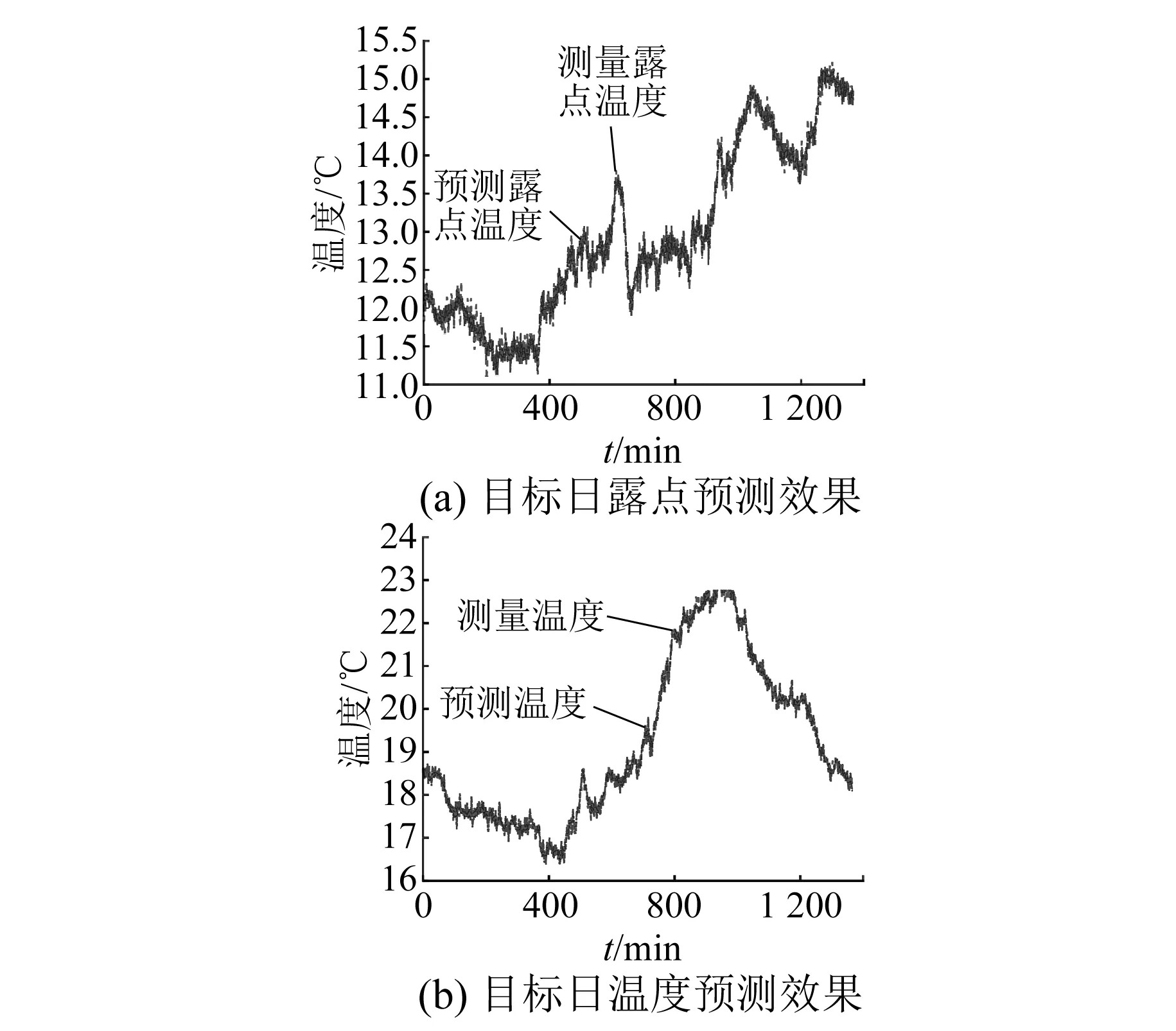
图5 目标日露点、温度的真实值与时间序列预测值对比

假定气象信息预测阶段是完全准确的，也即向SVM模型代入真实的气象数据，由此得到的光伏功率预测值的误差为支持向量机光伏功率预测阶段的误差。综合各阶段的误差，分析如表4所示。

表4 各阶段误差分析

完整预测流程的预测效果如图6所示。

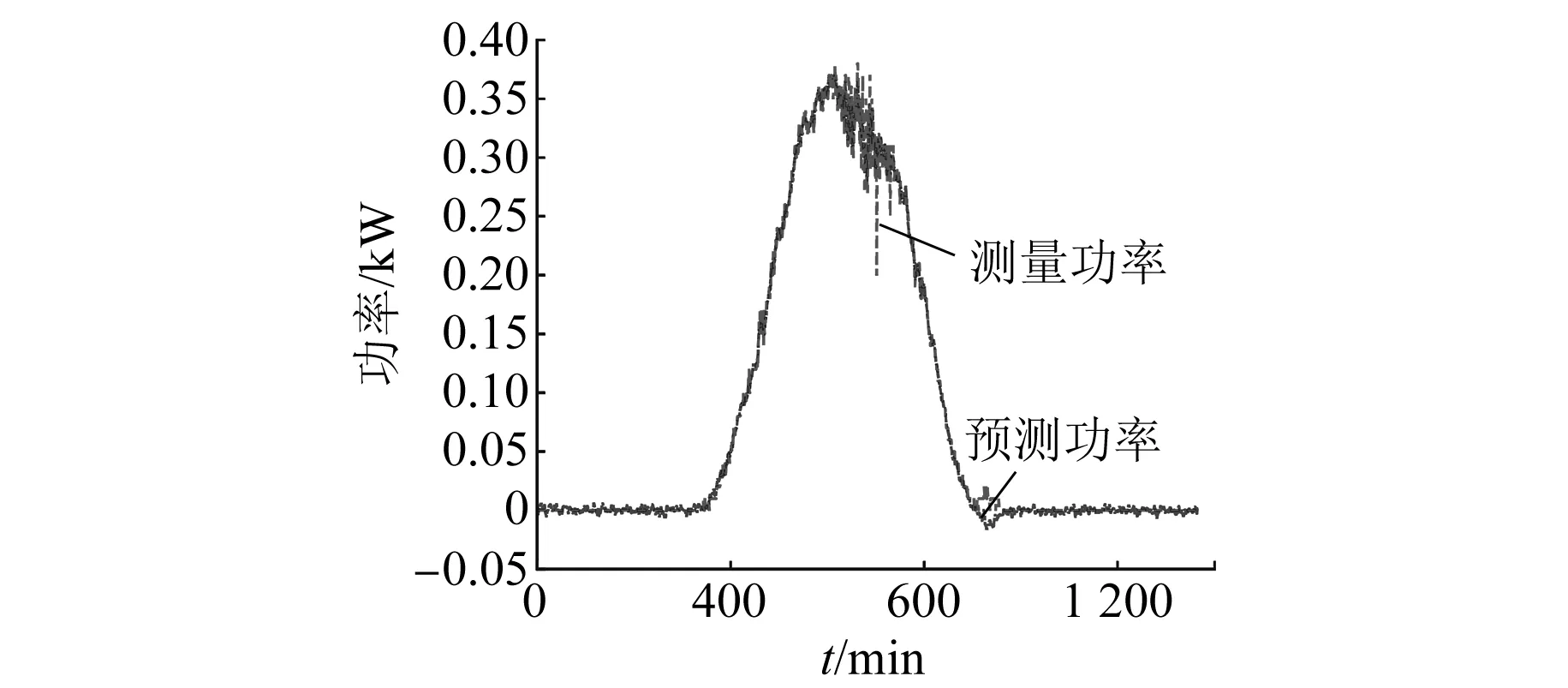
图6 预测值与真实值对比图

对比光伏发电功率的测量值和预测值，结合上文的分析能够发现，时间序列方法可对目标日的各种气象信息进行预测，作为支持向量机模型的输入。再由支持向量机回归模型求得目标日光伏发电功率，说明了预测方法的有效性。

此外，将春夏和冬季典型日以及阴天典型日作为预测对象，验证预测算法，其结果如图7所示，图7(a)～图7(d)分别为春夏和冬季以及阴天典型日的功率预测结果。

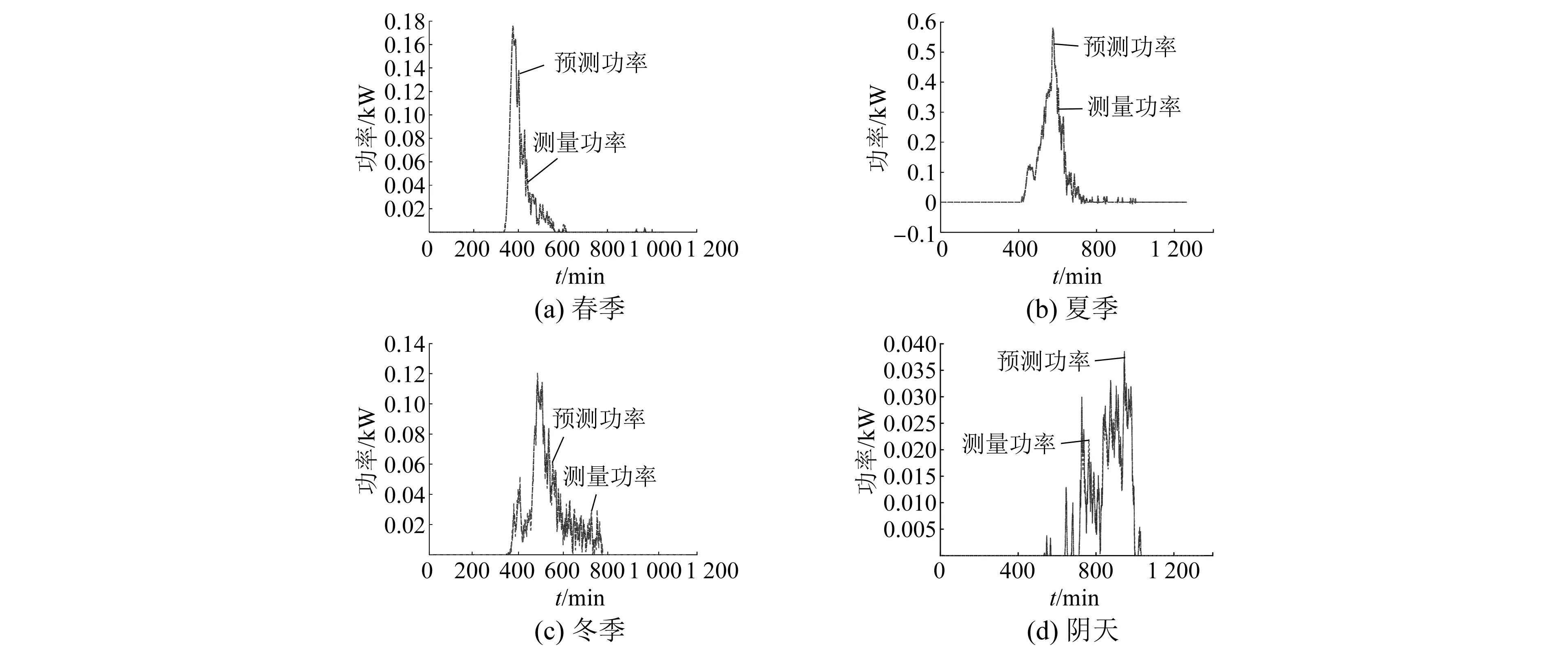
图7 春夏冬季及阴天典型日功率预测结果

春夏冬季及阴天4个典型日的功率预测误差如表5所示。

表5 典型日预测误差 kW

3.5 算法比较

为进一步验证本文所提MA-SVM算法的有效性，将本文的相关结果与相似研究及其他实现类似功能的预测算法进行比较。比较指标在RMSE的基础上增加了平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、最大偏差δMAX，其结果对比如表6所示。

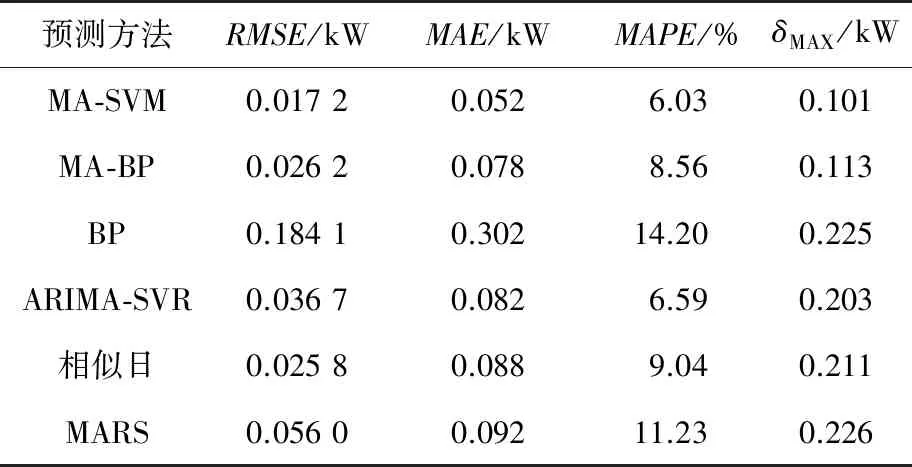
表6 光伏功率预测误差对比

通过对比多种算法的集中误差评价指标，可以发现，MA-SVM方法具有较为明显的优势。

4 结 语

本文通过建立完整的预测流程以及应用实际的试验平台验证，得到了一种有效的光伏功率短期预测方法。

(1) 采用实际试验平台釆集的辐照度等气象数据对相同地点的光伏发电平台的功率进行预测，釆用三次指数平滑法对目标日的气象信息进行预测，克服了类似的研究中辐照度数据与光伏功率不匹配的问题，解决了之前研究中采用真实的辐照度进行功率预测中的伪准确性问题，提高了预测的准确性与实用性。

(2) 气象条件变化的整体循环周期是一年，通过长期的运行，可以获得不同季节、不同气候条件的气象因素与输出功率的对应关系，随着数据库的扩充，预测的准确性将不断提高。