基于小波暂态能量比值的牵引网单端方向保护

陈仕龙，李朋松，庄启康，毕贵红，高敬业，赵四洪

（昆明理工大学 电力工程学院，云南 昆明 650500）

0 引言

近年来，电气化高速铁路在交通运输中所占比例越来越大[1]。

传统牵引供电系统存在的电流分相、电流负序等问题，对轨道交通运输的高速重载发展需求造成了很大的制约[2,3]。

电力电子技术的日渐成熟，给牵引供电系统快速稳定发展创造了条件。比如，依托电力电子器件构建的系统，可取消电流分相环节，提高系统运行的稳定性[4]。

贯通式同相牵引供电系统因在提高电能质量、系统稳定性等方面具有明显优势，所以目前已成为研究及应用热点[5]。

受沿线环境以及机车负荷冲击等因素影响，牵引网线路故障可能性较高，亟需探讨可靠的牵引网线路保护方案[6]。

现阶段，牵引网的保护主要为距离保护。文献[7]利用供电臂两相之间的电压以及谐波电流提出了馈线距离保护和电流速断保护。文献[8]通过串入高频阻波器识别故障行波波头，利用多测点测距方程进行故障测距。该方法测距精度高，但未考虑串入阻波器对牵引供电系统的影响。文献[9]分析了牵引网故障行波在不同频段、不同路径的传播特性，通过Morlet小波变换对故障信号进行处理，进而得到故障测距方案。

对于同相牵引供电系统而言，现有研究主要集中在系统特性方面——针对同相牵引供电系统的控制策略、系统稳定性以及提高电能质量等问题的研究较为深入，而对牵引网保护方面的研究还相对较少[10-12]。文献[13]利用高压直流输电线路正方向区内外故障暂态功率的频带差异性，构造了一种单端量保护；该方法为牵引网保护提供了研究思路。

同相牵引供电系统独特的供电方式，导致其系统结构特性与传统牵引供电系统存在明显差异，故需进一步探讨与之相适应的保护方案。

本文以贯通式同相牵引供电系统为研究对象，提出了一种利用小波高、低频暂态能量比值来区分牵引网线路区内、外故障的单端方向保护方案。

1 系统结构及边界频率特性分析

1.1 贯通式同相牵引供电系统结构

贯通式同相牵引直接供电系统基本结构如图1所示（电流正方向与机车运动方向一致）。

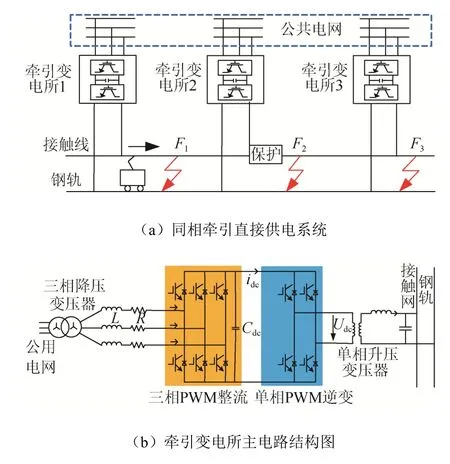
图1 牵引供电系统拓扑结构图Fig. 1 Topological structure diagram of traction power supply system

图1中，牵引变电所是供电系统主要组成部分，其使用的是PWM三相整流–单相PWM逆变对称变换与双闭环PI控制技术。牵引变电所的作用是：在消除公共电网与牵引供电系统之间相互干扰的同时，实现三相交流–直流–单相交流变换，使牵引网侧电压具有相同幅值和相位，实现无电分相环节情况下全线贯通供电。

变电所出口处并联的 LC滤波器，能有效滤除电流谐波、提高电能质量。

1.2 牵引网边界频率特性

牵引变电所出口处的 LC滤波器在起到滤除谐波作用的同时，其并联电容和一段牵引网线路还构成牵引网物理边界，如图2所示。

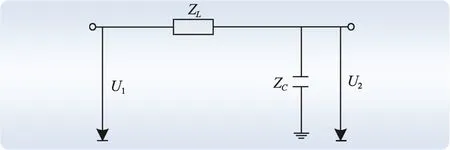
图2 牵引网边界等效模型Fig. 2 Equivalent model of traction network boundary

图2中ZL为牵引网一段线路的等效阻抗，ZC为牵引变电所供电段区外所并联电容的等效阻抗。

根据线路等效参数[14]和文献边界定义[15]，可计算牵引网边界传递函数G(jω)。

定义边界传递函数为U2/U1，即：

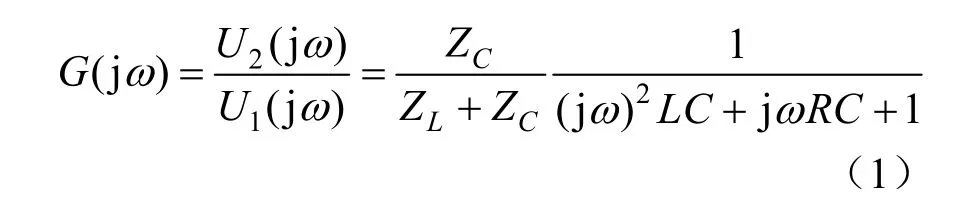
由此可得直接供电系统牵引网边界幅频特性G(jω)，如图3所示。

图3 牵引网边界幅频特性Fig. 3 Amplitude frequency characteristics of traction network boundary

由图3可知：对于频率在0～550 Hz频段的信号，其G(jω)≥1；当频率f≥800 Hz时，其幅值远小于1，且随频率的增加持续呈下降趋势。可见，牵引变电所供电段区外所并联的电容与牵引网的一部分线路共同构成的线路边界，是信号高频部分产生较大幅值衰减的主要影响因素。

2 牵引网故障暂态过程分析

2.1 反方向故障特征分析

正向区内线路末端发生非金属性接地故障产生的高频分量，将会受到线路波阻抗及过渡电阻2方面的影响；而反向区外靠近线路保护安装处，故障高频分量只受到线路边界衰减单方面影响，所以：有可能出现正向区内线路末端故障保护装置检测到的高频分量小于反向区外近保护安装处故障产生的高频分量；这将造成保护误动作。因此，单靠边界元件，即依靠高频分量大小区分区内、外故障将遇到一定困难，需要在保护安装处增加方向元件来有效区分正方向与反方向故障，从而消除保护死区。

考虑到实际工程应用问题，本文采用暂态功率能量极性来区分正反方向故障[16]。

规定电流正方向为母线流向线路，从而可以得到以下结论：当发生反方向故障时，保护装置测得的暂态电流Δi与暂态电压Δu突变方向相同；当发生正方向故障时，保护装置测得的暂态电流Δi与暂态电压Δu突变方向相反。

定义暂态功率ΔP=ΔiΔu。经计算，得到线路不同位置故障暂态功率ΔP，如图4所示。

图4 正反向故障暂态功率变化曲线Fig. 4 Transient power change curve of forward and reverse faults

由图4可以看出，暂态电流、电压突变方向的异同造成了暂态功率幅值变化的不同，故可利用暂态功率的极性判别故障发生的方向。

2.2 正方向区内外故障特征分析

2.2.1 高频暂态量提取

多尺度小波分解能够很好地表征故障信号高、低频带的信息：通过正交小波基对故障信号进行逐层的快速分解，每一层分解的结果都包含了一组高频段信息与低频段信息，即信号的细节部分与近似部分。该方法在频域分析方面具有优良的性能，广泛应用于非平稳信号的处理。分解过程可表示为：

设J为信号分解的最大尺度，第j尺度下的逼近信号表示为Aj，细节信号表示为Dj。选取合适的信号采样频率，利用高通滤波器h对逼近信号Aj进行相关滤波处理后，采用偶次降采样即可得到j+1尺度下的细节系数Dj+1。保留j+1尺度下的细节系数Dj+1后再对逼近信号Aj+1进行分解，逐层分解后可得到原始信号在各个频带上的细节系数[17,18]。分解过程如图5所示。

图5 多尺度小波分解示意图Fig. 5 Schematic diagram of multiscale wavelet decomposition

定义第j个尺度下信号的小波能量为：

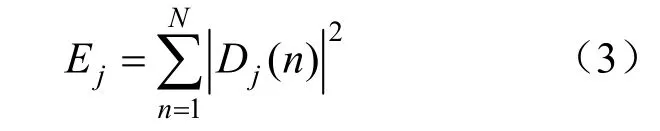
式中：Ej代表j尺度下的小波能量；Dj(n)为小波分解系数；N为采样点个数。

本文采用小波多尺度对故障电流信号的线模分量进行分解，以得到信号的多频带能量信息。考虑需要利用信号的高频分量进行分析，将采样频率设置为50 kHz，选取db5小波为小波基，多尺度分解6层。每个尺度对应频带如表1所示。

表1 不同分解尺度所对应的频带Tab. 1 Frequency bands corresponding to different decomposition scales kHz

据表1可知，D1尺度下的小波能量为故障电流信号的高频能量，D6尺度下的小波能量为故障电流信号的低频能量。

2.2.2 正方向区内外故障特征

如图1（a）所示，F1、F2、F3分别表示牵引网故障发生的不同位置。根据叠加原理，牵引网线路区内F2点发生接地故障以及区外F3点发生接地故障后的附加网络，如图6、图7所示。

图6 牵引网区内故障附加网络Fig. 6 Fault additional network in traction network area

图7 牵引网区外故障附加网络Fig. 7 Fault additional network outside the traction network area

图6—7中：ZL1、ZL2、ZC分别为牵引变出口处一部分线路的等效阻抗、牵引网线路剩余部分的等效阻抗、牵引变供电段区外所并联电容的等效阻抗。

区内故障时，故障电流行波IL只经过线路流向检测点，故障信号的高频能量E1和低频能量E6未经过边界的衰减，其幅值应较大。

区外故障时，故障电流行波IL经过线路、线路边界流向检测点，故障信号的高频能量E1和低频能量E6经过线路和边界的衰减，其幅值应小于区内故障信号高、低频能量幅值；但对于故障信号的低频能量而言，其衰减程度远不及高频能量。因此，利用故障信号的高、低频暂态能量比值，与保护装置预先设定好的整定值进行数值大小的对比，就可以判断故障发生的位置。

当牵引网线路发生接地故障时，对故障电流信号进行多尺度小波分解，可得故障信号高频、低频暂态能量谱。

以典型故障——金属性接地故障与高阻性接地故障为例，能量谱如图8、图9所示。

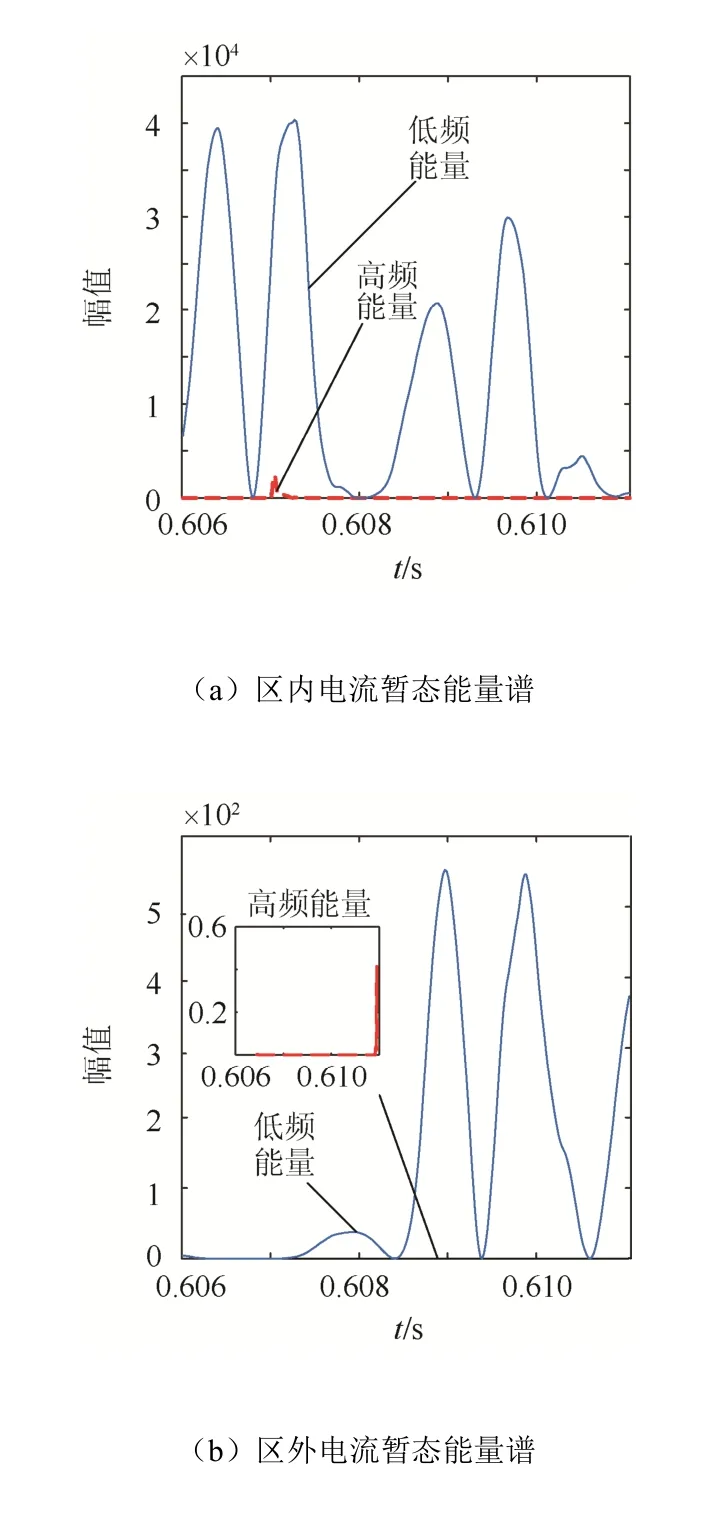
图8 区内外中点经0.1 Ω过渡电阻接地故障时电流暂态能量谱Fig. 8 Current transient energy spectrum in case of neutral point grounding fault through 0.1 Ω transition resistance inside and outside the area

图9 区内外中点经300 Ω过渡电阻接地故障时电流暂态能量谱Fig. 9 Current transient energy spectrum in case of grounding fault with 300 Ω transition resistance at the midpoint inside and outside the area

由图8、图9可知，无论对于金属性接地故障还是高阻性接地故障，牵引网边界都对故障信号的高频部分具有强烈衰减作用。此特性使得区内、外故障时故障信号的高频能量存在明显差异，但对于低频能量而言，其差异相对较小。

通过上述分析可得出结论：利用小波多尺度分解提取故障电流的高、低频暂态能量，并用其能量比值区分区内、外故障具有可行性。

3 保护方案

当同相牵引供电系统正常运行时，其电流波形为标准正弦波。发生故障后，系统失衡，电流幅值急剧上升，故可采用电流的变化率作为故障启动判据。

3.1 方向判据

选取数据窗内电流突变量Δi及电压突变量Δu，经计算得暂态功率ΔP，再对暂态功率ΔP进行积分运算，便可得到暂态功率能量EP，即：

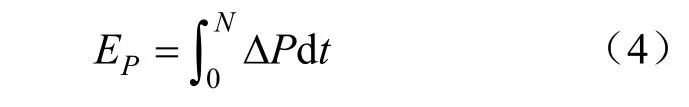
式中：N为采样点个数。

当发生反方向故障时，暂态功率能量EP>0；发生正方向故障时，暂态功率能量EP<0。

3.2 正向区内外故障判据

对保护装置采集的故障电流信号进行6尺度小波分解，求取第1尺度高频能量E1和第6尺度低频能量E6。定义E1与E6的比值KP为：

式中：K为比例系数。

设置K目的是保证暂态能量能够较好地被保护装置测量到。综合考虑采样频率及时间窗长度，取K=1 000。

利用此高低频能量比值作为区内外保护动作判据：当KP满足式（6）时，故障发生在保护区内，保护动作；反之则为区外发生故障，保护不动作。

式中：Kset为保护动作阈值。

经过仿真验证并考虑保留一定裕度，取Kset为1。

保护流程如图10所示。

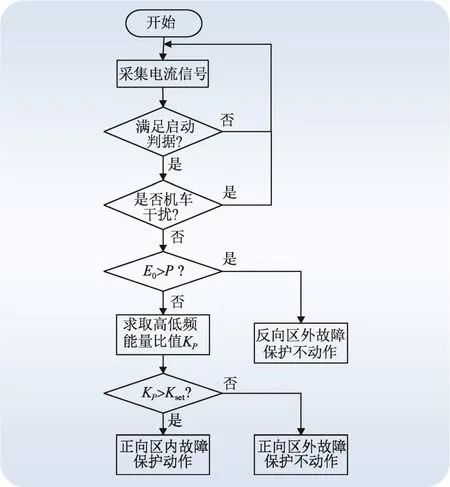
图10 保护方案流程图Fig. 10 Flow chart of protection scheme

4 仿真研究

本文利用PSCAD/EMTDC仿真软件搭建了贯通式同相牵引直接供电系统仿真模型。仿真模型参数：公用电网侧电压为 220 kV，牵引网侧电压为27.5 kV，系统频率为50 Hz，电源容量为6 GVA；牵引变之间的线路长度为35 km；采样时间选取5 ms。

4.1 不同故障初始角仿真实验

选取不同故障初始角，分别在牵引网线路的不同位置设置相同过渡电阻（50 Ω）接地故障。

表2为保护方向判别及高低频能量比值计算结果。由表2数据可见，保护对于不同故障初始角接地故障均能准确动作。

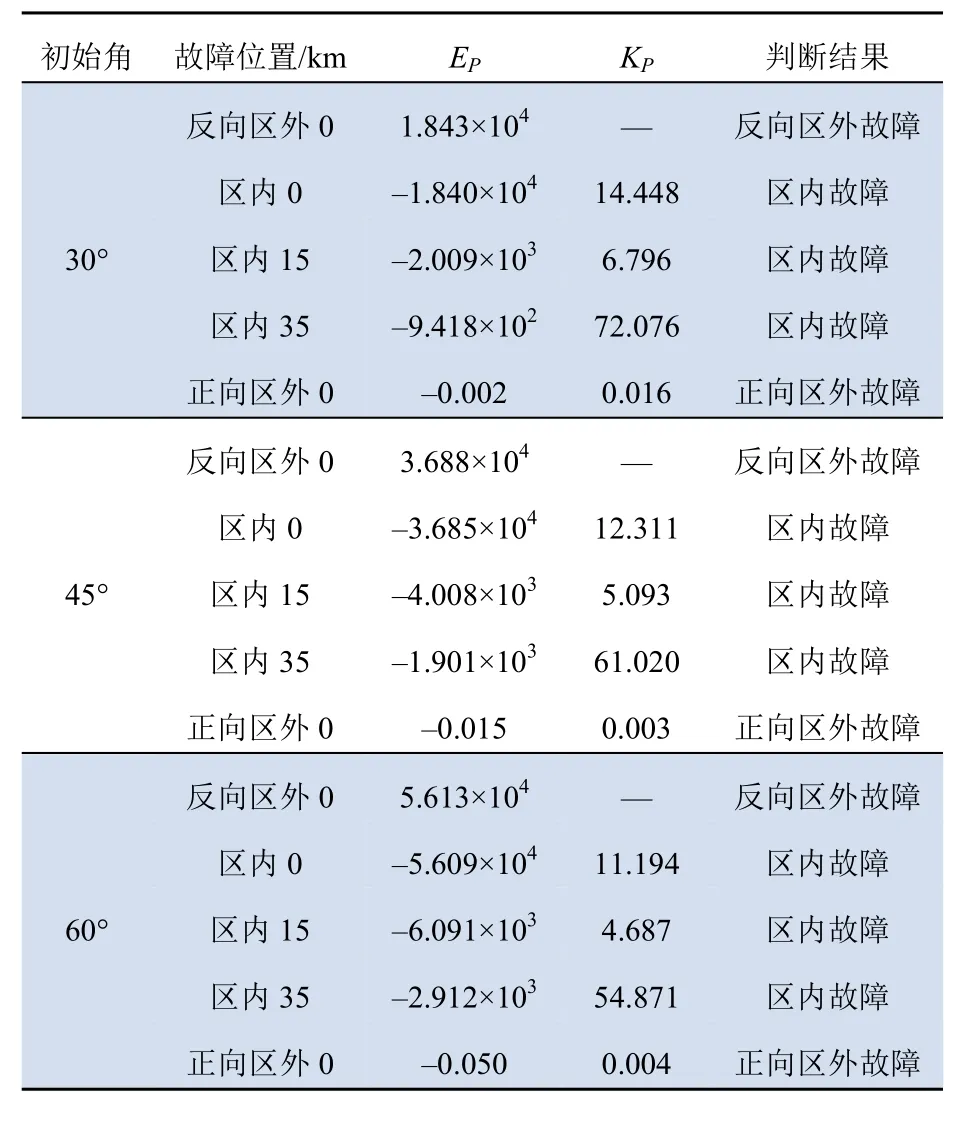
表2 不同故障初始角保护判断结果Tab. 2 Judgment results of different fault initial angle protection

4.2 不同故障距离仿真实验

选定相同故障初始角（45°），在线路不同位置，以5 km为间隔距离，设置相同过渡电阻（0.1 Ω）接地故障进行仿真。

仿真结果如表3所示。

表3 不同故障距离保护判断结果Tab. 3 Judgement results of different fault distance protection

从表3可以看出，线路能够得到可靠保护。

4.3 不同过渡电阻仿真实验

仿真故障设置：相同故障初始角（60°），正方向不同位置，过渡电阻分别为 0.1 Ω、10 Ω、50 Ω、100 Ω、300 Ω；故障距离同样以首端、中点、末端为例。

仿真结果表4所示。

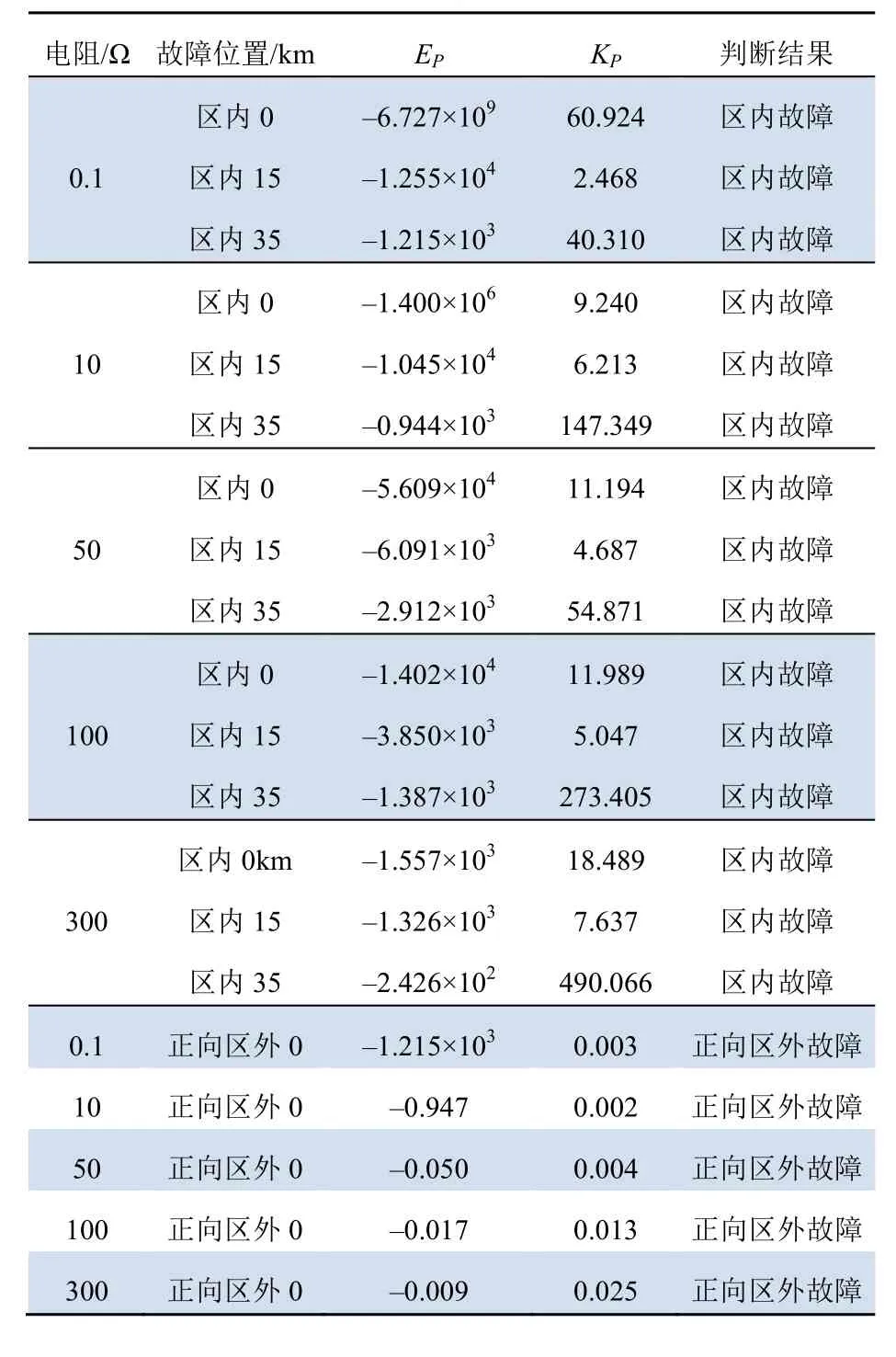
表4 不同过渡电阻保护判断结果Tab. 4 Judgment results of different transition resistance protection

由表4所示仿真结果可知，对于不同的故障位置、不同故障初始角、不同故障距离、不同过渡电阻，本文所提保护方案均能准确可靠判别。

5 结论

本文利用牵引网边界对故障电流信号高频部分的衰减作用以及正反方向故障时暂态功率能量极性的差异，提出了一种基于小波暂态能量的牵引网单端量方向保护方案。

方案可快速准确地区分牵引网线路区内、外故障，在不同过渡电阻、不同故障初始角情况下均能可靠判别。

（1）牵引变电所供电段区外所并联的电容与牵引网的一部分线路共同构成的线路边界是故障电流信号高频部分产生较大幅值衰减的主要影响因素。

（2）线路反方向故障时，暂态功率能量的极性与正方向故障时的极性相反。

（3）线路正方向故障时，利用小波多尺度分解可提取故障电流信号的高低频暂态能量，通过比较区内外故障时的高频暂态能量与低频暂态能量比值可构造正方向区内外故障判据。