页岩气高效开采中钻井完井和水力压裂的关键力学问题1)

高 岳 王 涛 †, 严子铭 柳占立 庄 茁

* (清华大学航天航空学院，北京 100084)

† (北京理工大学机电学院，北京 100081)

引言

郑哲敏先生是中国力学学科建设与发展的组织者和领导者之一,在国内外享有崇高的声誉和影响力.他对祖国的热爱、对科学的追求、对事业的执着,奉全部智慧创新,高山仰止,是后人学习的楷模;郑哲敏学长是清华大学的杰出校友.他热爱母校,亲自为清华大学工程力学研究班讲课,亲手创建钱学森力学班,培养了一大批力学拔尖创新人才,倾毕生心血育人,春风化雨,令晚辈永远铭记.

郑先生关注国家能源战略的重大需求和发展态势,推动页岩气高效开采中的工程科学问题研究.2014 年12 月10—11 日,郑哲敏和黄克智等院士发起香山科学会议第517 次学术讨论会,主题是页岩气开发中的工程科学问题.研讨中国页岩气高效开采中的关键力学和石油工程科学问题,鼓励相关领域的学者重视这项研究工作.2015 年3 月19 日,郑先生邀请庄茁在中科院力学所做页岩水力压裂报告(见附录A).2017 年4 月11 日,93 岁高龄的郑先生驱车前往位于河北省廊坊市的中石油勘探开发研究院廊坊分院,亲自调研页岩大物模水力压裂试验过程(见附录B).他希望我们带他到重庆涪陵山区页岩水力压裂施工现场调研,并提出在四川锦屏数千米深部岩体做高围压条件下的水力压裂实验.遗憾的是他的这些夙愿未能付诸成行.作为晚辈和学生,愿谨以此文,纪念郑哲敏先生.

页岩气是指以吸附和游离时而还有流体相的状态赋存于泥页岩中的非常规天然气,我国探明储量丰富,地域分布广泛,页岩气开采已成为我国绿色能源开发的重要领域[1-4].与北美地区相比,我国页岩气埋藏深,赋存条件差,自然丰度低,因此,高效开采面临更多的困难和挑战[1,5].围绕页岩气高效开采中的力学和石油工程挑战性科学与技术问题,本文研究了钻井完井和水力压裂缝网改造等关键力学问题.第2 节提出了页岩多孔弹性介质的本构、强度和断裂韧性各向异性模型;第3 节阐述了钻井完井过程中的多孔弹性介质井壁稳定性和剪切破坏的时间效应;第4 节描述了水平井水力压裂技术,包含水力裂缝扩展的大物模实验技术,水力压裂过程中耦合流体/固体/裂缝扩展的数值模拟方法,以及川渝地区的水力压裂施工现场实践应用.第5 节建立了数据驱动的页岩气采收率预测方法.

1 页岩的各向异性基本力学性质

作为含有薄片层状层理的沉积岩,页岩往往表现出较强的各向异性.本节将从本构、强度、以及断裂韧性角度分别介绍页岩的各向异性模型.

1.1 页岩多孔弹性介质的各向异性本构模型

页岩是由黏土经压力及温度作用构造形成的沉积岩,其中多存在薄页状或片状的层理.由于上覆地层的压实作用及层理面影响,页岩表现出很强的各向异性[6];而在微米与纳米尺度上,页岩则呈现出非均匀且多孔的特征[7],其中蕴藏着期望开采的页岩气.因此,页岩是一种典型的非均质各向异性多孔充液介质.图1 展示了一种典型的多孔弹性介质结构,包含固体骨架、充液连通孔隙、及不连通孔隙三部分.

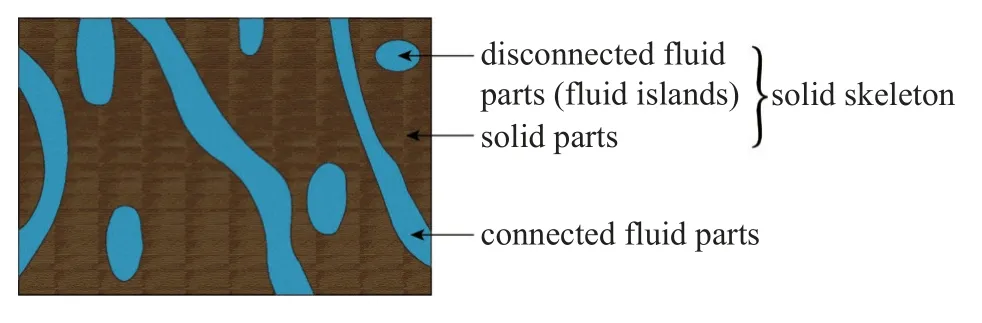
图1 多孔弹性介质示意图Fig.1 A diagram sketch of the poroelastic medium

在非均质多孔充液介质中,固体变形与孔隙流体渗流耦合在一起,其力学响应非常复杂.在固体力学中,此类介质往往采用多孔充液弹性本构模型表征.这是Biot 在1940 年代提出的本构模型[8-11],其中引入两个新的流体场变量:孔隙压力p和孔隙流体体积分数变化量 ζ,避免了直接处理复杂的孔隙细节,而是将整个多孔材料视为一个连续的弹性介质.如同广义胡克定律中应力场 σij与应变场 εij的关系,孔隙压力p与流体体积分数变化量 ζ 也是一组功共轭的场变量.在一般各向异性多孔弹性本构中,它们之间的关系可以由四阶柔度弹性张量Mijkl、二阶张量mij,以及一个宏观材料常数CCH所确定[12-15],即

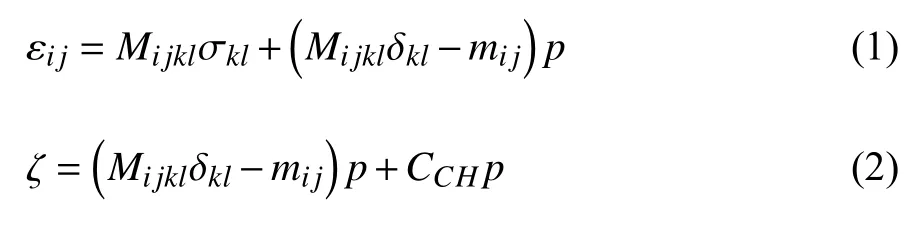
式(1)和式(2)是线性增量模式最一般的形式.在多孔弹性本构模型中,也经常使用Biot 有效应力系数张量作为材料常数,定义为

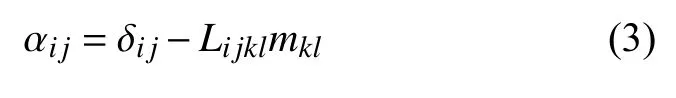
其中Lijkl为刚度弹性张量,为柔度张量Mi jkl在四阶等同张量Iijkl=下的逆.可见,在一般各向异性材料中,该本构模型有28个独立的材料常数.

多孔充液弹性本构模型成功诠释了在土壤与岩石的传统弹性力学中所不能解释的现象,如孔隙压力的Skempton 效应[16]、Mandel-Cryer 效应[17]、地面沉降[18]等,它是一维Terzaghi土壤压实模型的推广.由于孔隙流体扩散过程中内禀的时间尺度,该本构模型是时间相关的.通过将材料中的固体骨架和孔隙流体变形看作宏观连续介质,多孔弹性本构模型避免了测量固体骨架材料的弹性常数(如骨架刚度张量等).

Cheng[13,17]通过引入微观均匀与微观各向同性两个材料假设,将二阶张量mi j简化为了表征固体骨架材料体积变形的材料常数,即

其中Ks为固体骨架材料的体积模量.在该材料假设下,各向异性多孔弹性本构模型的独立弹性材料常数个数减少为23 个.

在工程实际中,由于地应力与地质构造作用,页岩一般可以视为横观各向同性介质,并假设其平行于节理面方向的材料属性与垂直于该面的属性不同.式(1)和式(2)提出的本构模型在横观各向同性条件下可得到进一步简化[19],其中柔度张量Mi jkl退化为横观各向同性广义胡克定律中由{E,E′,ν,ν′,G′}五个独立材料常数构成的张量,二阶张量mij亦退化为对角阵 d iag(m,m,m′).若进一步引入Cheng 提出的微观均匀与微观各向同性材料假设,本构模型所引入的独立材料常数个数简化为7 个(E,E′,ν,ν′,G′,Ks,CCH),其中材料常数CCH满足[13,15]

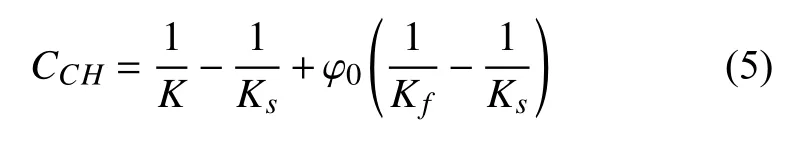
其中K,Ks,Kf分别为材料整体、固体骨架、孔隙流体的体积模量,φ0为多孔材料孔隙率.

应当注意的是,多孔弹性本构模型中的固体骨架相关材料常数(如Ks和等)是不易测得的量,实际应用中为完整测量页岩这类岩石的多孔弹性本构材料常数,一般需要结合封套试验、无封套试验、Π-loading 加载等多种测量手段[18],从而推算材料常数CCH的值.对于横观各向同性多孔弹性岩石,我们在结合了Makhnenko 等[20-22]针对低渗透率岩石设计的干样品测量比拟试验方案后,提出了相对更节省时间和工作量的材料常数测量方案[23],如图2所示.

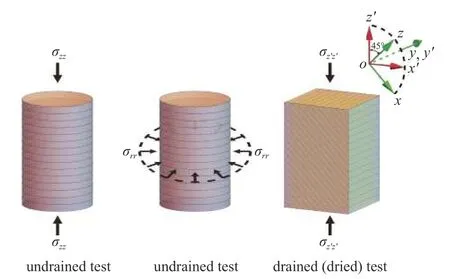
图2 横观各向同性岩石材料常数测量方案示意图Fig.2 Loading scheme diagrams of the transversely isotropic poroelastic material constants measurement

1.2 页岩强度与断裂韧性的各向异性

页岩是一种典型的各向异性材料,其各向异性不仅表现在表征材料变形过程的本构模型中,也表现在其强度与断裂韧性特征中[24-28].

Cho 等[29]分别使用单轴压缩及巴西圆盘试验测量了Boryeong 页岩在加载方向与节理面呈不同夹角状态下的单轴压缩与拉伸强度.结果表明该组页岩的单轴抗压强度UCS 在加载方向平行或垂直于节理面时最高,夹角约为 45°时最低,整体呈U 型曲线,这亦符合理论预期.巴西圆盘试验结果表明节理面与加载方向平行时岩石最易发生破坏.

Fjaer 等[30]针对Mancos 页岩开展研究,他们在传统的弱面模型基础上引入了平行于节理面的非均匀微裂缝模型,该模型更好地预测了在Mancos露头页岩中测得的单轴压缩强度及杨氏模量随加载方向变化的情况.该结果呈现出有所偏斜的U 型曲线.

页岩的断裂韧性同样表现出各向异性的特征.Chandler 等[31]测量了Mancos 页岩的性质,他们发现对于垂直于层理面方向的断裂韧性为0.72 MPa·m1/2,而平行于层理面方向的断裂韧性只有0.21 MPa·m1/2.实际上,岩石断裂韧性的强各向异性不仅表现在页岩等沉积岩,Nasseri 等[32]测量了Barre 花岗岩中裂缝在两垂直方向下的断裂韧性,分别为1.89 MPa·m1/2与1.14 MPa·m1/2,他们也发现裂缝在高断裂韧性方向上的扩展路径会更加曲折.Kataoka 等[33]分别对于非洲花岗闪长岩和韩国花岗岩这两种各向异性岩石测量了断裂韧性,发现垂直于层理面方向的断裂韧性值比平行于层理面方向的值高出 29%.

为了有效处理岩石中断裂韧性各向异性的特征,我们引入了断裂韧性的弱面模型[34-36].假设岩石的断裂韧性Gc(θ) 是与裂缝扩展方向 θ 有关的函数,其在特定方向 α (即节理面)上的值Gcw相对于其他方向Gc0较低,如图3 所示.

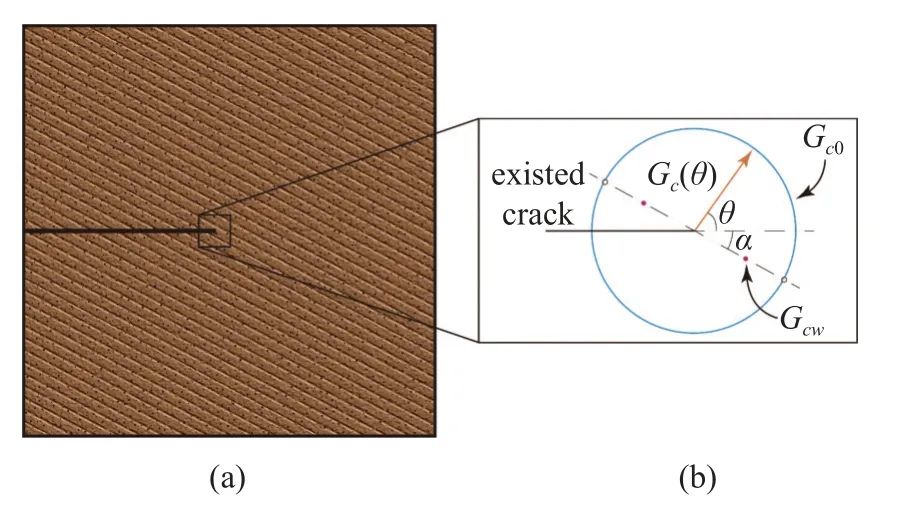
图3 (a) 含弱面岩石中裂缝示意图,左侧黑色实线表示当前裂缝位置,斜线表示岩石中弱面方向.(b) 裂缝朝 θ 方向扩展的断裂韧性Gc(θ),α 表示弱面方向.在几乎所有方向上,G c(θ) 都为 G c0,除了弱面方向 α 之外,此处 G c(θ) 值为GcwFig.3 (a) A sketch of the crack inside a rock with the weak plane.(b) The fracture toughness G c(θ) varies with fracture propagation direction θ,where α denotes the weak plane direction.

我们基于最大应变能释放率准则(MERR)分析了弱面模型下裂缝的扩展规律,指出裂缝扩展方向仅与当前裂缝方向与弱面方向的夹角 α,弱面相对强度比值Gcw/Gc0,以及裂缝扩展前的应力强度因子比值KII/KI三者有关[34].基于该结论进一步提出裂缝扩展禁止区[35],即在给定弱面相对强度Gcw/Gc0下,由于弱面对裂缝的吸引效应导致裂缝与弱面附近不能扩展的角度范围.通过理论推导证明了该禁止区范围可由如下两个等价的表达式定义

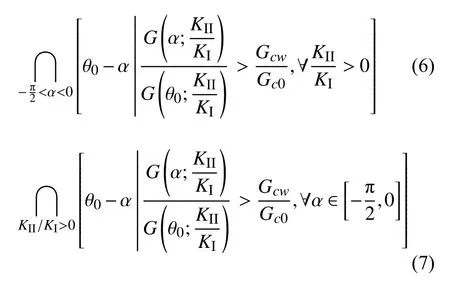
图4 展示了裂缝扩展禁止区在Gcw/Gc0=0.9,α=-π/12条件下的范围,其中右侧数字表示了应力强度因子比值KII/KI取对应值时裂缝的扩展角度;而橙色区域指出当-0.0988＜KII/KI＜0.472 时,裂缝将沿弱面方向 α=-π/12 方向扩展.即橙色区域内的裂缝扩展方向被禁止了.

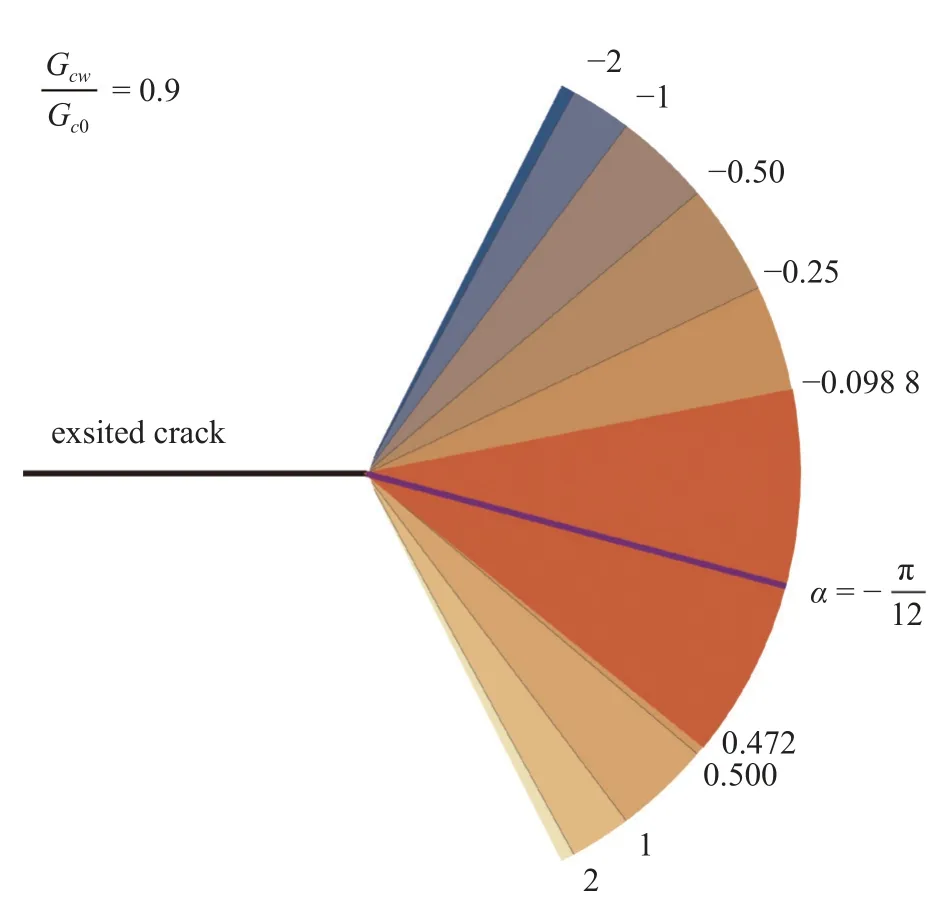
图4 裂缝扩展禁止区在 G cw/Gc0=0.9,α=-π/12 状态下的范围Fig.4 The crack extension forbidden area of G cw/Gc0=0.9,α=-π/12

2 钻井完井的井壁稳定性问题

钻井液的压力控制是钻井工程的关键技术难点之一[37-38].在每段钻进过程中,高压钻井液直接接触钻开的岩石壁面,起到稳定钻井井壁的作用.然而,如果钻井液压力过低,一般会发生井壁垮塌事故,即剪切破坏;反之,如果钻井液压力过高,井壁往往会产生裂缝,导致钻井液漏失到岩层中,即发生拉伸破坏.在固体力学问题中,井壁岩石是否发生拉伸与剪切破坏,一般分别采用拉伸破坏条件与莫尔库仑准则分别判断.但是,对于含孔隙充液的岩石,应当基于多孔充液弹性本构模型考察其破坏条件.

在当前工程实践中,人们往往把岩石中的初始孔隙压力看作类似地应力的地质状态常数,并不会随钻井过程改变;这种方案基于广义胡克定律,在对岩石分析其弹性变形后,一般将该初始孔隙压力乘Biot 有效应力系数叠加到应力解中[39],进而得到修正后的应力解,并使用这个应力解作为安全校核.我们基于多孔弹性本构模型重新考察了该问题[14,19,40],指出了上述简单叠加方法的局限性.

2.1 基于多孔弹性本构模型的井壁稳定性问题

对于主应力方向与井壁轴向平行的钻井过程,其复杂的应力及孔隙压力边界条件可通过叠加原理等效分解为地应力及3 个子模式叠加,如图5 所示.

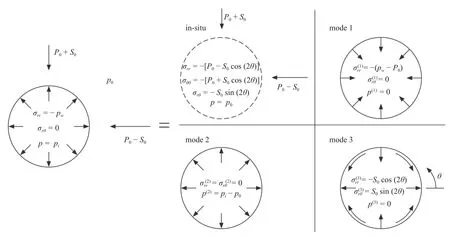
图5 井眼问题载荷分解图示Fig.5 The loading decomposition of the borehole problem

由边界条件可知,模式1 与2 的解是轴对称的,而模式3的解是对于极坐标角 θ 二阶谐波的,即{ c os(2θ),sin(2θ)}.如2.1 节所述,使用多孔弹性本构模型求得的解一般是与时间相关的.Detournay 等[41]针对该问题的分析指出模式1的求解结果将恰好与时间无关,并给出了基于拉普拉斯变换方法求解出的模式2 和3 的频域解.尽管由频域解获取全时域的解只能通过数值拉普拉斯逆变换,但仍可以基于初值与终值定理由频域解获得短时(t≈0+) 及长时(t→∞)状态下全场的应力解[40].

对于包含有孔隙压力场p的多孔弹性介质,分析其破坏模式时有必要将传统的拉伸破坏准则及莫尔库仑准则加以修正以考察孔隙压力带来的影响.文献[17,39,42]均对此问题展开过讨论,他们一致认为在分析含孔隙岩石的破坏模式时,应当采用Terzaghi 等效应力,即将=σij+pδi j直接代入到传统的拉伸与剪切破坏条件中分析,而非采用Biot有效应力 σij+αpδi j的形式.基于Terzaghi 等效应力的破坏准则也与实验结果更相符[43-45].纳入孔隙压力场的拉伸破坏准则与莫尔库仑准则可分别写作

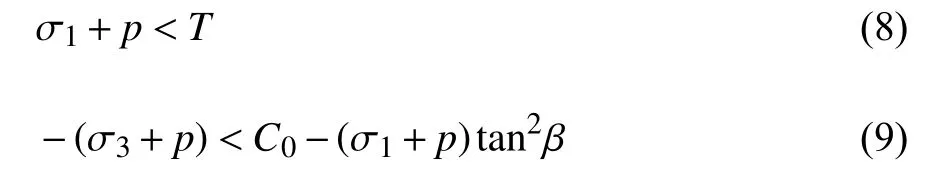
式中,T与C0分别为抗拉强度及单轴压缩强度,β=π/4+φ/2 且有 φ=arctanμ 为内摩擦角.本节采用拉伸为正、压缩为负的应力记号,以 σ1与 σ3分别表示最大与最小主应力.在真实地质环境中,一般有0 ＞σ1＞σ3.

考虑到拉伸破坏有水平与竖直两种破坏模式,剪切破坏中主应力顺序有六种不同可能,所有的拉伸及剪切破坏共有八种可能的形式.我们求解出了瞬时和长时下全场的应力与孔隙压力场,并提取出了“瞬时”、“短时”、“长时”三个最危险的状态[19,40].在综合考虑了各个时刻及各破坏位置处的应力场与孔隙压力场后,对于各向同性多孔弹性岩石及横观各向同性多孔弹性岩石总结出了八种失效模式下对应的破坏位置、时间、以及破坏种类,并给出了井壁极限压力解析解,以方便工程直接使用.

图6 在一组特定的地应力条件及岩石材料参数下,对比了分别基于广义胡克定律及多孔弹性本构模型得到的井壁安全工作压力范围pw随其横坐标P0=(σH+σh)/2为水平平均地应力变化情况.可见在该问题中,使用广义胡克定律是偏于危险的.

图6 井眼许可工作压力对比:(a) 广义胡克定律,(b) 多孔弹性本构Fig.6 A comparison of allowed borehole pressure obtained by:(a) the generalized Hooke’s law and (b) the poroelastic constitutive model

2.2 井壁剪切破坏的时间效应

套管损坏问题是页岩气开采中的一个重要问题,套管损坏的频繁发生严重威胁了页岩气井的高效、安全、经济开发[46-48].井壁剪切破坏是套管损坏的诱因之一,本小节针对一例特定的横观各向同性岩石井壁剪切破坏过程进行分析,通过全场时域解指出使用多孔弹性本构模型分析剪切破坏的必要性.

本小节以Aoki 等[49]基于无渗试验与封套试验方法测得的一组横观各向同性页岩材料常数进行分析

其中MCH为与CCH有关的另一多孔弹性材料常数[14-15].

取莫尔库仑准则中强度参数为β=60°,C0=65 MPa,考察该岩石在水平地应力 σH=30 MPa 与σh=10 MPa,及初始孔隙压力p0=10 MPa 下的全场应力.通过将莫尔库仑准则改(9)写为最大剪应力τmax与平均正应力的形式

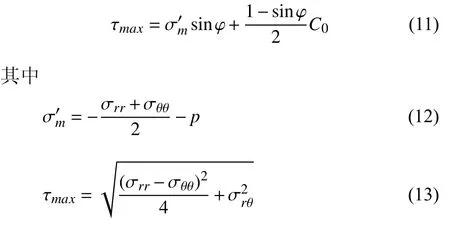
对于每个给定的时间,图7(a)也画出了数值解在全场的图像(从r=a至r→∞).从图中可见,井壁边界的应力状态连续地由瞬时解(点A)移动到长时解(点C).但是,无穷远处(r→∞)的应力状态,对于任何有限的时间,一直停留在了同一个点D;直到t→∞时才突然跳跃到了点E.这里的不连续性来自于对t→∞和r→∞ 取极限顺序的区别.

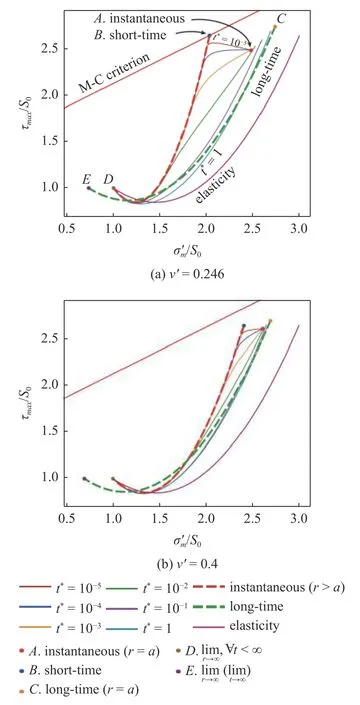
图7 在莫尔平面上多孔弹性岩石Terzaghi 等效应力场的数值计算结果Fig.7 The variation of Terzaghi effective stress field with time on the Mohr plane for the poroelastic rock material

图7(a)中将莫尔-库仑准则式(11)用一条直线表示.任何一个高于这条直线的点,都意味着该处发生剪切破坏.可见短时解的点B恰好落在了图中所画的莫尔-库仑准则直线上.这是符合预期的,因为画图时所用的pw=13.59 MPa 正是选择了短时解破坏的临界值.

传统广义胡克定律弹性解所求得的应力状态也画在了图7(a)上.弹性解与时间无关,从图中可以看出,弹性解远低于莫尔-库仑准则直线.这意味着对于这种加载状态,广义胡克定律将预测井眼不会发生剪切破坏.对于这个例子,经典的弹性解处于偏危险的一侧,这再一次表明了多孔弹性本构模型对于井眼安全问题的重要性.

图7(b) 画出了更改泊松比ν′=0.4时的情况,同时保持了地应力和井壁载荷不变.此时,多孔弹性本构和广义胡克定律都预测剪切破坏不会发生.

通过与使用广义胡克定律的结果比较,在大多数强度分析情况下,我们发现使用多孔弹性本构关系进行井眼安全校核是非常必要的.因此建议在石油工程问题中使用多孔弹性本构模型代替广义胡克定律进行分析计算.

3 水平井水力压裂技术

页岩气高效开采的另一关键技术是水平井水力压裂.美国页岩气革命的成功,其中一个主要的原因是水平井水力压裂技术在21 世纪初的快速发展.

3.1 水力裂缝扩展的大物模实验技术

为了研究水力压裂问题,理解在页岩压裂过程中的缝网形成机制,在中石油勘探开发研究院廊坊分院进行了水力压裂大物模实验[50].

典型的大物模水力压裂实验装置如图8(a) 所示,该装置位于中石油勘探开发研究院廊坊分院酸化压裂中心[51].通过在露头岩样或人工制备的岩样(岩样的尺寸为710 mm × 710 mm × 914 mm)的中间部位打一个竖直的井孔,在岩样周围加三向围压,其中,上覆垂向压力为24 MPa,水平方向最大地应力为24 MPa,水平方向最小地应力为10 MPa,以此模拟地下岩样的真实环境.通过在竖直井孔注入高压的液体(压裂液),驱动岩石内部的初始裂缝扩展(或者岩石内部破裂产生初始裂缝并扩展).为了观察压裂后水力裂缝的状态,对压裂液进行染色,压裂后切开岩样,观察被染色的区域,判断裂缝的扩展与分布情况.压裂后切开岩石看到的裂缝形态如图8(b)和8(c)所示,分别对应砂岩和页岩的典型压裂实验效果.砂岩由于其均匀各向同性的特点,压裂形成的水力裂缝通常是硬币型的单一裂缝,而页岩由于其各向异性和非均质性,水力裂缝扩展的过程中伴随着分叉、汇合等,形态非常复杂,通常表现为裂缝网络.

图8 (a)大物模实验装置,(b)典型的砂岩和(c)页岩的压裂实验结果Fig.8 (a) Large physical object experimental device,(b) typical sandstone fracturing experimental results and(c) typical shale fracturing experimental results

页岩是一种典型的层状各向异性材料,其中广泛分布着各种层理面、天然裂缝和断层,这些薄弱面对页岩储层的地质力学性质有着显著的影响,在压裂过程中对形成复杂裂缝网络起着重要的作用[52-53].因此,有必要通过实验研究层理弱面对水力裂缝扩展的影响.

在中石油勘探开发研究院廊坊压裂中心进行了含有层理的岩石(铸造水泥块)的大物模水力压裂实验,实验设置如图9 所示.岩样尺寸为600 mm × 600 mm ×900 mm,水平设置两个600 mm × 600 mm 的层理面,通过在铸造水泥块的过程中预埋纱网实现特定位置层理面的预制.采用120 mL/min 的流体流量排空管线和注入井孔,正式压裂采用恒定排量10 mL/min进行压裂,观察破裂压力及裂缝延伸压力.

图9 含有层理弱面的岩石的水力压裂大物模实验示意图Fig.9 Schematic diagram of large object model experiment of hydraulic fracturing of rocks with bedding plane

实验中测得的三向地应力水平、井口压力和入口流量(排量)如图10 所示.可以看出,大物模实验装置可以很好地控制三向地应力的水平,W/E 水平应力为7 MPa,N/S 水平应力和垂向应力均为13 MPa.水泥块的破裂压力约为9.6 MPa,此外,在压裂的过程中,井口压力曲线始终高于W/E 水平应力而低于N/S 水平应力和垂向应力,说明裂缝始终保持垂直于最小水平主应力的方向(W/E 水平方面)扩展,这些可在水泥块压裂后的剖面中观察到.

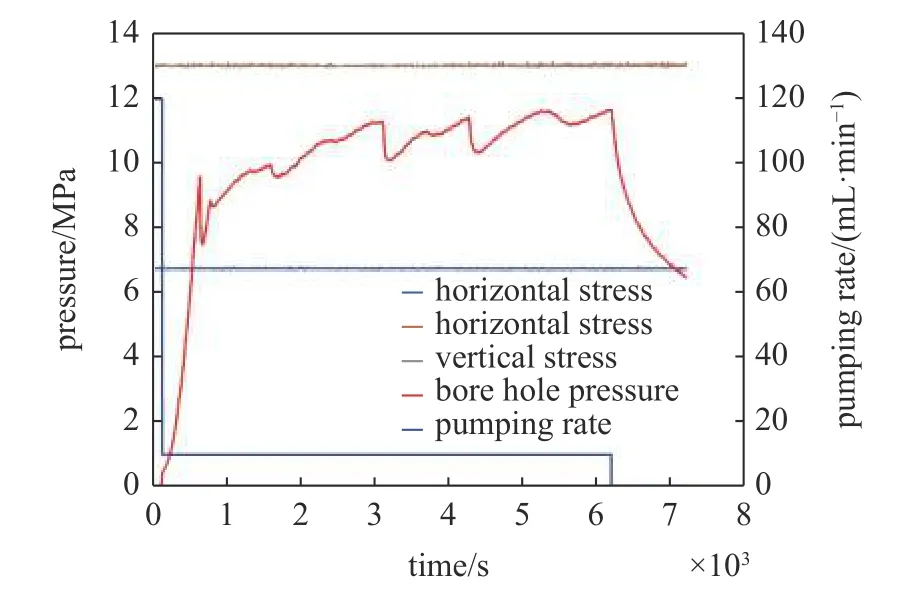
图10 含有层理面的水泥块大物模水力压裂实验过程中的测得的三向地应力水平、井口压力和入口流量Fig.10 Measured three-dimensional in-situ stress value,wellhead pressure and inlet flow during large object model hydraulic fracturing experiment of cement block with bedding plane

图11 给出了含有层理弱面的水泥块在水力压裂后的剖面图.在压裂过程中,可以看出产生南北向扩展(垂直于最小水平地应力的方向)的裂缝,裂缝整体上呈一条直线,但略有弯曲,与前面通过井口压力获得的判断一致.此外,裂缝贯穿上下弱面,并且压裂液进入了上层的水平弱面中.因此,可以合理地猜测,图10 中的井口压力在压裂过程中的突变,可能是由于压裂液进入了水平层理弱面内,导致了井口压力的瞬时快速下降.

图11 含有层理弱面的水泥块在水力压裂后的剖面图Fig.11 Profile of cement block with bedding plane after hydraulic fracturing

3.2 水力裂缝扩展的数值模拟

由于深部岩石样品难以获得,一般采用露头岩样进行水力压裂实验,但是实验成本昂贵.因此,通过数值模拟研究水力压裂是一种有效的方法,受到了研究者的普遍关注[54-58].多孔弹性介质中的水力压裂过程是一个固体变形、裂缝扩展和流体流动的全耦合问题[59],它包含以下几个方面:(1)介质中的孔隙压力引起固体的膨胀或收缩,而固体的变形又会影响介质中的孔隙流动;(2)裂缝内的流体能够驱动裂缝张开和扩展,而裂缝张开宽度又会影响裂缝中的流体流动;(3)裂缝中的流体会滤失到多孔介质中,从而导致缝内流动和多孔介质渗流的耦合.因此,在进行水力压裂数值模拟时,必须考虑以上几个因素,同步进行求解.

3.2.1 岩石的变形与断裂

岩石的断裂失效过程非常复杂[60],尤其是考虑到流体的作用后的岩石失效过程,涉及到多种机制相互作用[61-63].这里,只考虑多孔弹性介质的脆性失效,一个典型三维多孔介质的水力压裂过程的模型示意图如图12 所示.模型的初始构型为 Ω0,当前构型为 Ω.岩石中含有一些不连续面,如水力裂缝,用ΓD表示.

图12 含有水力不连续面(水力裂缝)的三维多孔介质的示意图Fig.12 schematic diagram of three-dimensional porous media containing hydraulic discontinuities (hydraulic fractures)

水力压裂缝网改造是准静态过程,因此,固体的动量方程采用更新的拉格朗日格式为

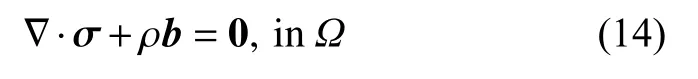
这里,σ 是柯西应力,∇ 是材料梯度,b是体力向量,ρ是多孔介质的平均密度,定义如下:ρ=(1-φ)ρs+φρw.其中,φ是多孔介质的孔隙度,ρs和 ρw分别是固体骨架和孔隙流体的密度.

岩石的增量形式的线弹性本构方程为

这里,D是多孔介质的全渗状态下的刚度矩阵,ε 是多孔弹性介质的应变,σ′′是Biot 有效应力,定义为

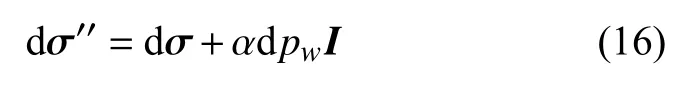
其中,pw是流体的孔隙压力,I是单位张量.

采用小应变假设,则多孔介质的应变可以用位移表示为

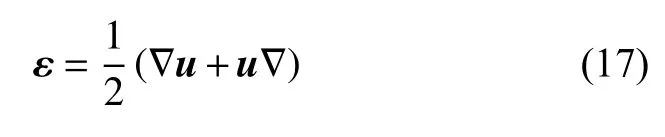
通过联立式(14)～式(17),可以得到增量形式的固体变形偏微分方程

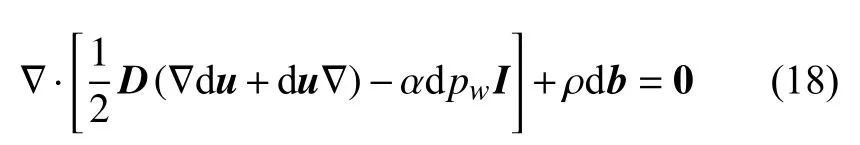
对于固体的断裂过程,假设裂缝扩展的方向总是垂直于最大主应力方向.在线弹性断裂力学(LEFM)中,当能量释放率G等于材料能量释放率的极限值GIC(断裂韧度)时,裂缝扩展.当材料内聚区的尺寸比裂缝长度小得多时,断裂韧度GIC等于I 型裂缝的拉伸应力-张开位移曲线下的面积,并可由下式定义

其中,E′是平面应变杨氏模量,定义为

3.2.2 多孔介质中流体的流动

页岩是一种含有孔隙流体的多孔弹性介质,孔隙流体会在压力差的驱动下发生渗流过程.假设多孔弹性介质中的流体总是处在饱和状态,则孔隙流体的连续方程为[17]

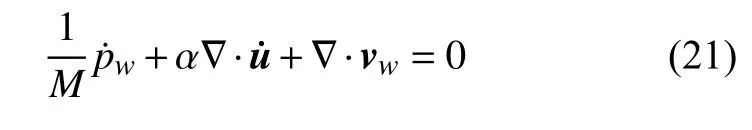
其中,vw是多孔弹性介质中孔隙流体的达西速度向量,其量纲为 L T-1.这里忽略了孔隙流体的惯性效应和黏性效应,则孔隙流体的线动量方程(达西定律)为

这里,kw是多孔弹性介质中孔隙流体的渗透率张量.

上面的方程即为岩石基质中孔隙流体流动的控制方程,通过对其进行离散并求解,可以得到多孔弹性介质的全场渗流解.

3.2.3 水力裂缝内流体的流动

不同于岩石基质中的孔隙流体渗流,由于水力裂缝是一个较大的流动通道,流体在水力裂缝内的流动是一个比较快速的流动过程.由于水力裂缝宽度方向的尺寸远小于另外两个方向的尺寸,因而水力裂缝内流体的流动满足层流流动的条件.因此,水力裂缝内流体流动的质量守恒方程为

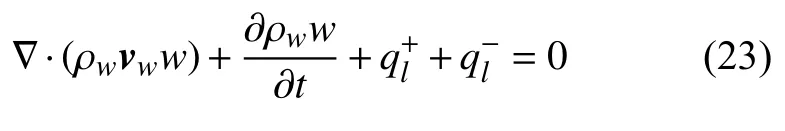
式中使用孔隙流体速度向量vw而非缝内流量速率q=wvw表示,因而式中右侧为裂缝宽度w的平方.

通过水力裂缝的上下表面向基质的滤失会导致基质中和水力裂缝内的流体之间的传质耦合.这里假设压裂液是牛顿流体,并且滤失过程也满足达西定律,则通过水力裂缝上下表面滤失的流体的质量流量可写为

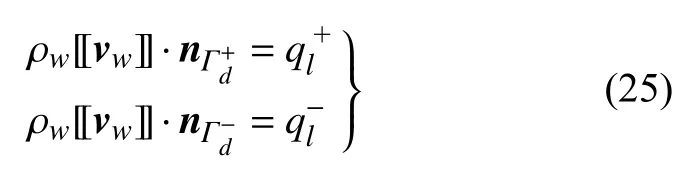
将流体速度式(26)代入质量守恒方程(23)中,经过一些推导后,可以得到如下表达式

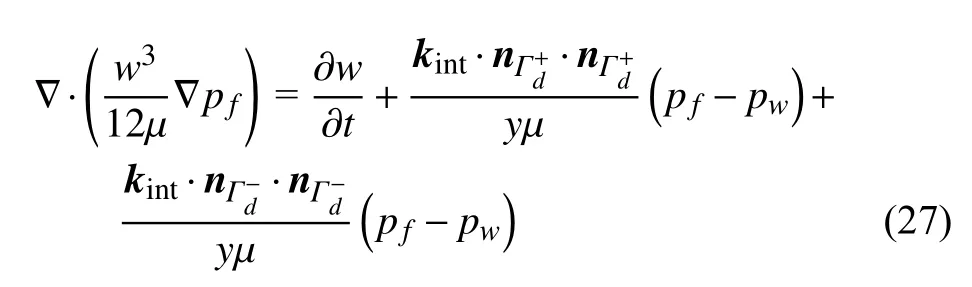
该方程即为水力裂缝内流体流动的控制方程,我们将在下一节中对其进行离散和求解.

3.2.4 页岩水力压裂的扩展有限元格式

常用的断裂问题的数值模拟方法包括边界元法[64]、相场法[65-67]、扩展有限元法[68]、内聚力单元法[69-70]等.这里,采用扩展有限元法进行离散和模拟.以位移场和压力场为求解的基本变量,采用标准的Galerkin方法进行空间离散.采用扩展有限元法离散位移场,引入附加自由度,可以避免重新划分网格.在XFEM中,位移场u可以分解为连续部分uC和非连续部分uD(附加自由度),其离散表达式如下[71]

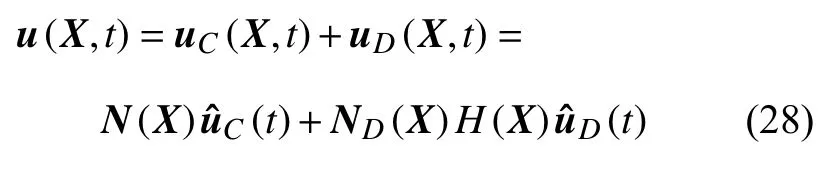
其中,N(X)和ND(X)分别是标准形函数向量和扩充节点的形函数向量.分别是节点位移的连续部分和非连续部分.H(X) 是Heaviside 函数,即阶跃函数,其定义如下

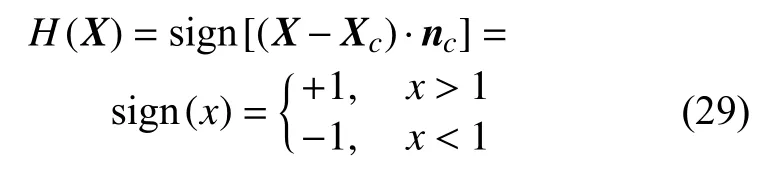
采用标准Galerkin 法分别对基质中的孔隙压力场和水力裂缝内的流体压力场进行离散

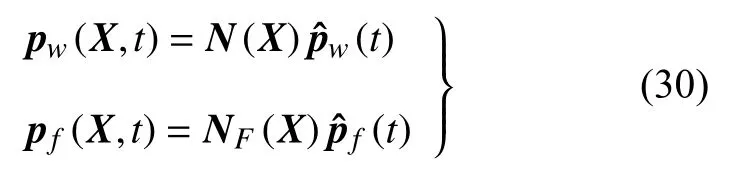
其中,NF(X) 是对应于裂缝表面的形函数.和分别是节点上的孔隙压力和裂缝内节点上的压力值.基于Bubnov-Galerkin 技术,含有水力裂缝的多孔弹性介质的控制方程的离散化形式为

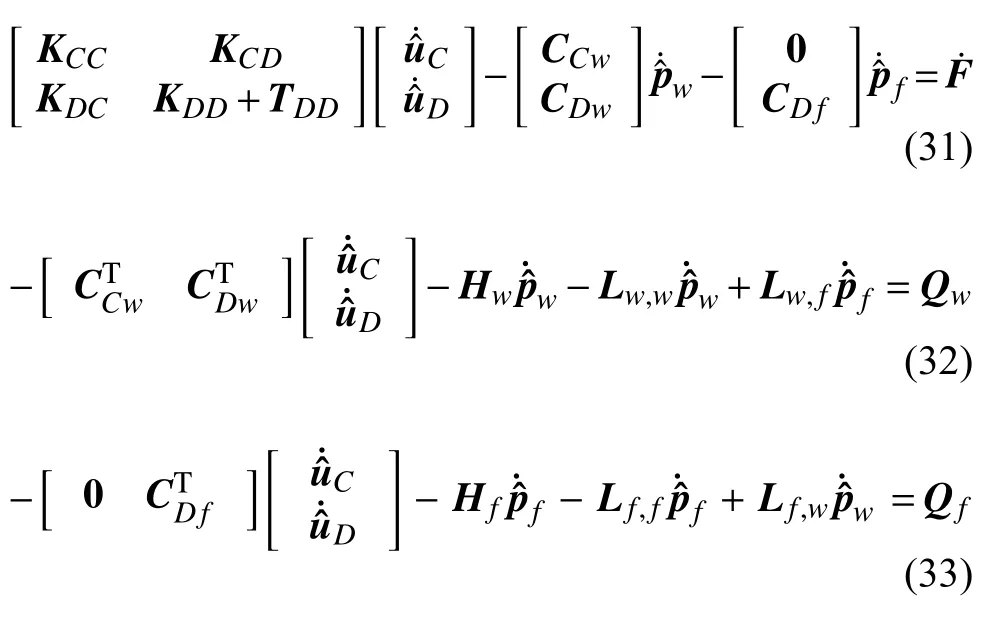
方程式(31)～式(33)即为多孔弹性介质的水力压裂问题的全耦合控制方程组,通过联合求解该方程组,可以得到全场的位移、孔隙压力和缝内流体的压力场.在得到问题的空间离散方程后,使用广义的Newmark 方法在时间域上进行离散.为了求解完全耦合的非线性方程组系统式(31)～式(33),在每个时间步实施牛顿-拉夫逊迭代算法.

3.2.5 黏性主导的硬币型裂缝的扩展

接下来通过上述理论和数值模型,模拟黏性主导的硬币型裂缝的扩展问题,一个典型的硬币型裂缝的扩展如图13 所示.由于模型的对称性,使用1/4 模型和对称边界条件,且通过46656 个六面体单元离散求解区域.

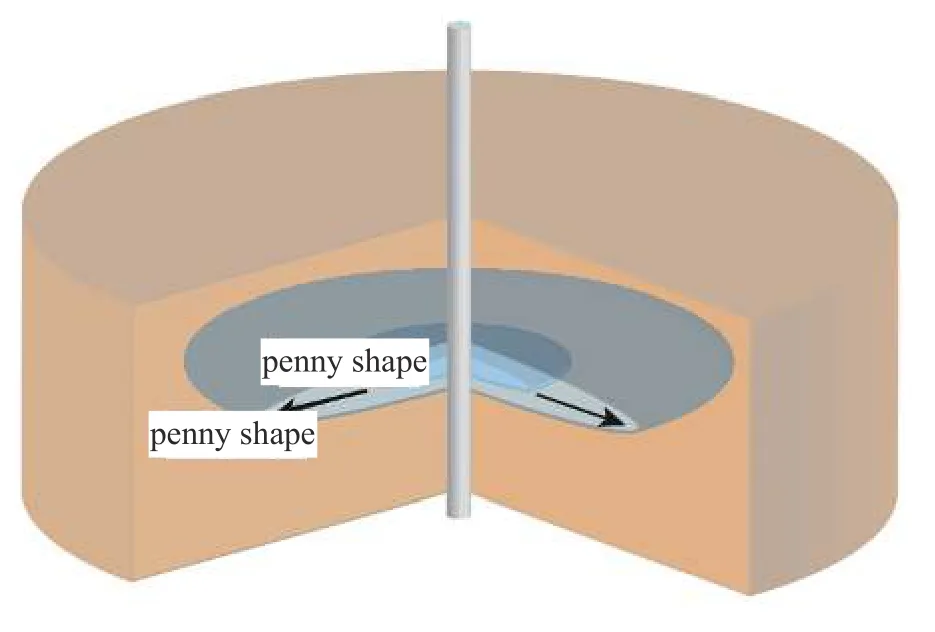
图13 典型的硬币型裂缝扩展的示意图Fig.13 Schematic diagram of typical penny shaped crack propagation

根据地层参数和泵注条件的不同,水力裂缝扩展的过程和机制也不同,对于硬币型裂缝,其扩展机制主要由如下的一个无量纲参数(无量纲断裂韧性)来控制[72]

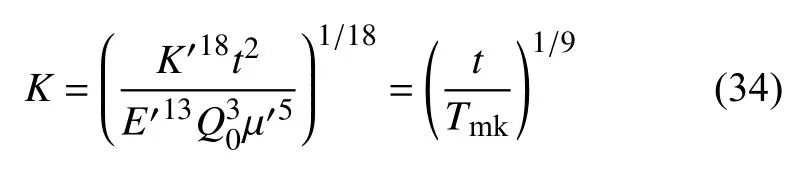
这里,材料参数K′和μ′分别定义如下

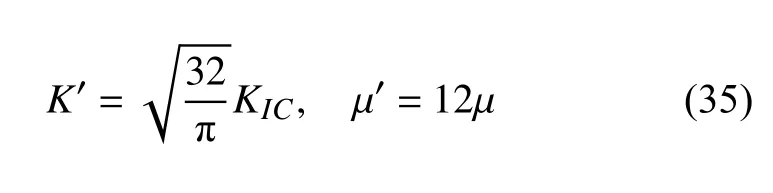
Tmk是这组参数下硬币型裂缝扩展的特征时间,定义如下

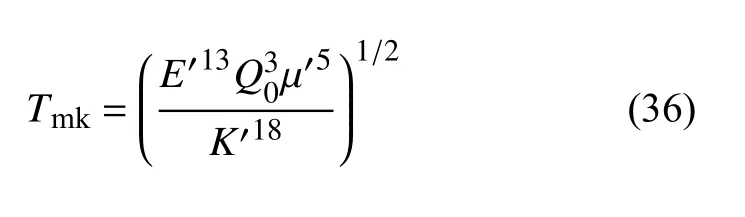
当无量纲断裂韧性K的值远小于1.0 时,硬币型裂缝的扩展机制为黏性主导,即系统的大部分能量耗散在黏性流体的流动过程中;而当无量纲断裂韧性K的值大于4.0 时,硬币型裂缝的扩展机制为韧性主导,即系统的大部分能量耗散在形成新的水力裂缝表面上.

在本算例中,通过选择合适的模拟参数使得水力裂缝在扩展的过程中始终为黏性主导.表1 中列出了黏性主导的硬币型裂缝扩展的模拟参数.在此参数下,无量纲断裂韧性K始终比1.0 小得多,这表明水力裂缝在扩展的过程中始终是黏性主导的[73],因此可以通过与零韧性条件下的解析解进行比较和验证.

表1 黏性主导的硬币型裂缝扩展的模拟参数Table 1 Simulation model parameters of penny shaped crack propagation dominated by viscosity

本节数值模拟的结果与理论解的比较如图14所示,分别为水力裂缝扩展半径R随时间的变化、不同时刻的水力裂缝前端位置、不同时刻的水力裂缝张开宽度的分布、和不同时刻的水力裂缝缝内流体压力分布的数值解与理论解的比较.从图中可以发现数值结果与解析解吻合得很好,说明上述模型可以用于求解三维水力压裂问题,且求解精度较高.

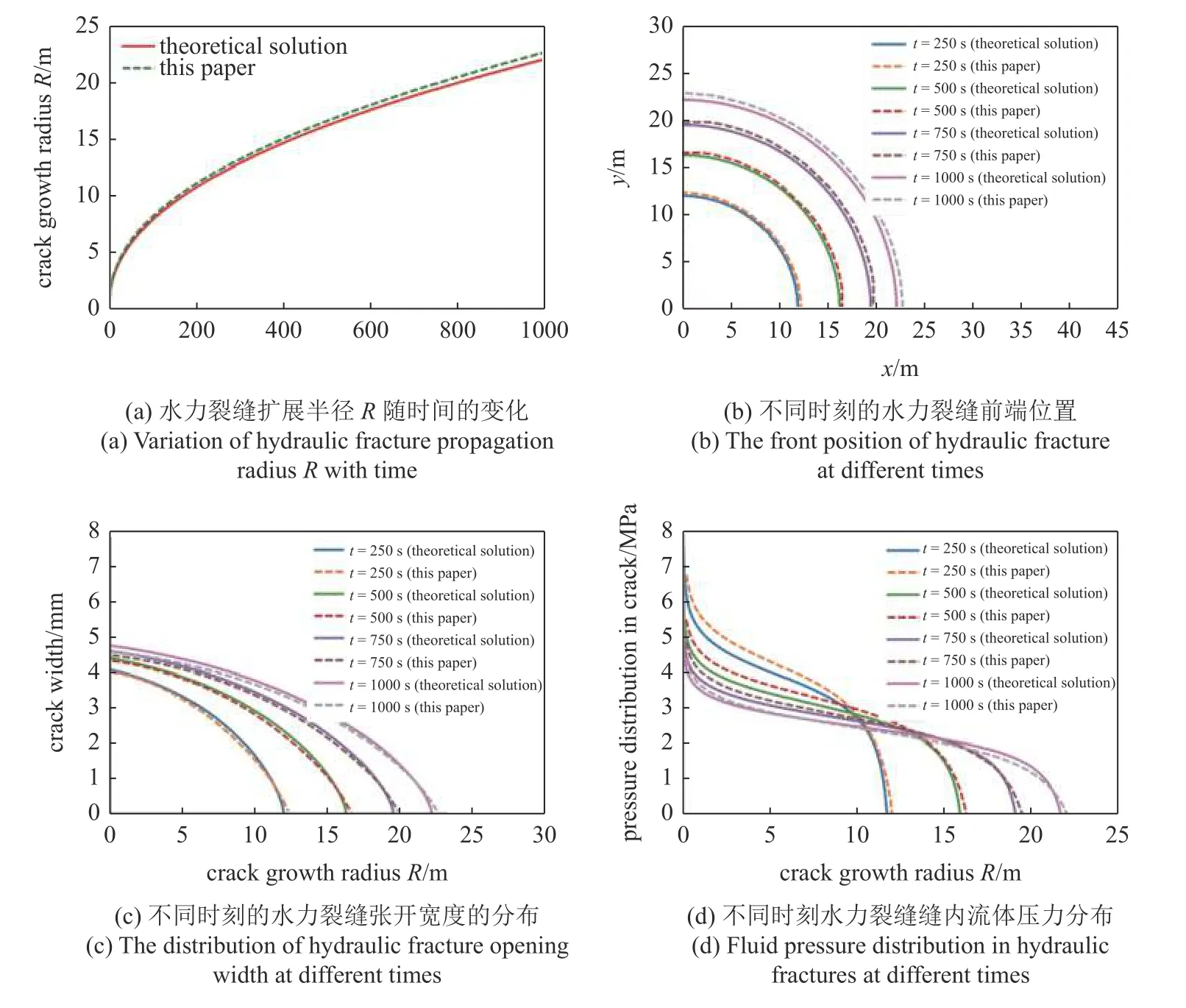
图14 数值模拟的结果与黏性主导的水力裂缝的理论解比较Fig.14 Comparison between numerical simulation results and theoretical solutions of viscous dominated hydraulic fractures

3.3 页岩水力压裂工程实践

本节中,通过对四川省内江威远204 号水平井的模拟,研究在实际的水平井水力压裂施工中的一个压裂段的多条射孔簇同时平行扩展的过程.现场施工条件、储层材料参数、初始地应力场等条件如下.

(1)压裂模拟的基本地质条件:根据威远204 井储层数据计算的结果,威远204 井页岩储层段(3486～3536 m)的最小水平地应力(72 MPa)与下部灰岩的最小水平地应力(72 MPa)基本一致,与上部泥岩的最小水平地应力(77 MPa)相差5 MPa 左右.当对本井水力压裂改造时,上部泥岩层的最小水平地应力较高,且泥页岩层的厚度较大,是较好的水力裂缝隔挡层.但要注意预防水力裂缝扩展并穿过下部较薄的灰岩层,造成压裂液的滤失.

(2)储层的材料参数:威远204 井压裂的地层材料参数和初始地应力场的分布经过均匀化后,分为5 个小层(分别是五峰组、龙-1a、龙-1b、龙-1c、龙-1d 层),每层内的材料参数值和初始地应力值是一致的,如表2 所示.此外,各层的岩石断裂韧性均取为1.46 MPa·m1/2.

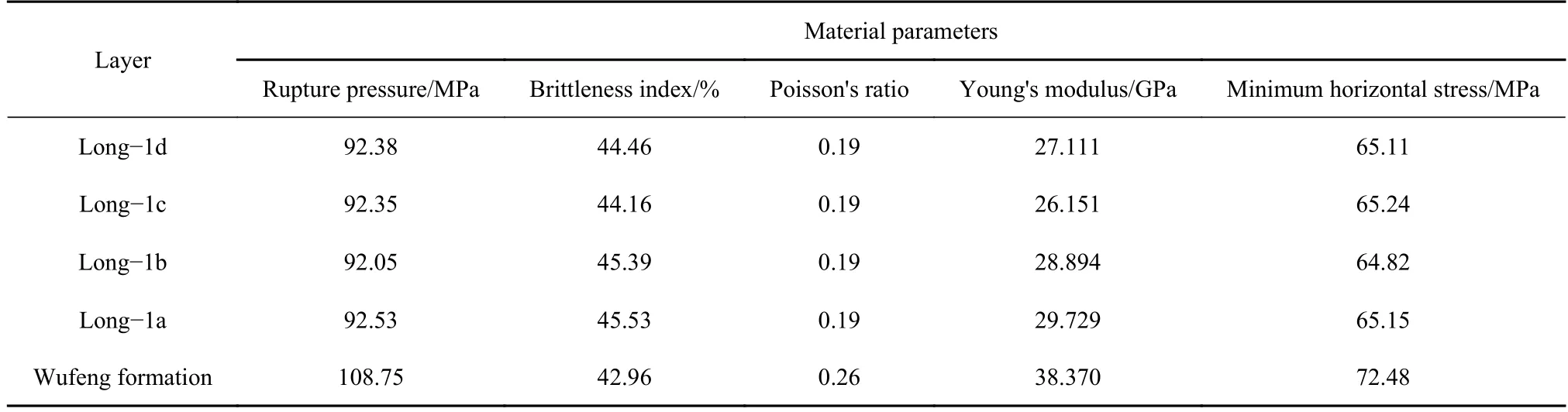
表2 威远204 井所在地层的材料参数和最小水平地应力Table 2 Material parameters and minimum horizontal stress of the formation where Weiyuan 204 well is located

(3)储层的初始地应力条件:储层的三向初始地应力与最小水平地应力的放大图如图15 所示,在垂深为3474～3490 m,和3535～3538 m 范围内,均有较高的初始最小地应力层,其平均初始最小地应力均在76 MPa 以上,可以有效阻挡水力裂缝的穿层,从而保证水力裂缝只在储层内扩展.

图15 威远204 井所在储层的两向初始地应力分布与最小水平地应力分布Fig.15 Two dimensional initial in-situ stress distribution and minimum horizontal in-situ stress distribution of the reservoir where Weiyuan 204 well is located

(4)水力压裂泵注施工过程:本井的施工井段的位置为:3690～3780 m (垂深3499～3536 m,射孔在垂深为3505 m 的位置,很靠近上覆盖层),对井的第11 个压裂段进行水力压裂施工.施工曲线和压裂液泵注流量如图16 所示.在水力压裂施工的过程中,压裂液的流量基本保持不变,为13 m3/min(0.217 m3/s),在模拟中直接用这个恒定的流量进行泵注模拟,泵注持续时间为2 小时40 分钟(9600 秒).

图16 威204 井压裂段的第11 段的施工曲线(包括注入流量、加砂量和泵注压力)Fig.16 Construction curve of the 11th section of the fracturing section of well Wei-204 (including pumping rate,sand concentration and pumping pressure)

(5)压裂段的射孔情况:这里模拟了一个压裂段,该段内有4 个射孔簇,4 个射孔簇之间的间隔依次为:18 m,19 m 和20 m,在数值模型中,每个射孔簇代表一条水力裂缝.

在本模拟中,主要关注在水力压裂过程中多条水力裂缝平行扩展的过程,同时考虑上下高应力覆盖层对水力裂缝缝高的限制作用[74],建立的有限元模型如图17 所示.根据地层材料属性和初始地应力场的分布情况,将模型简化为含有五层不同材料参数和初始地应力的岩层,每层的具体材料参数和初始地应力的分布情况根据上面给出的参数赋值,井的深度为3505 m(即井筒和射孔簇在垂深为3505 m的位置).

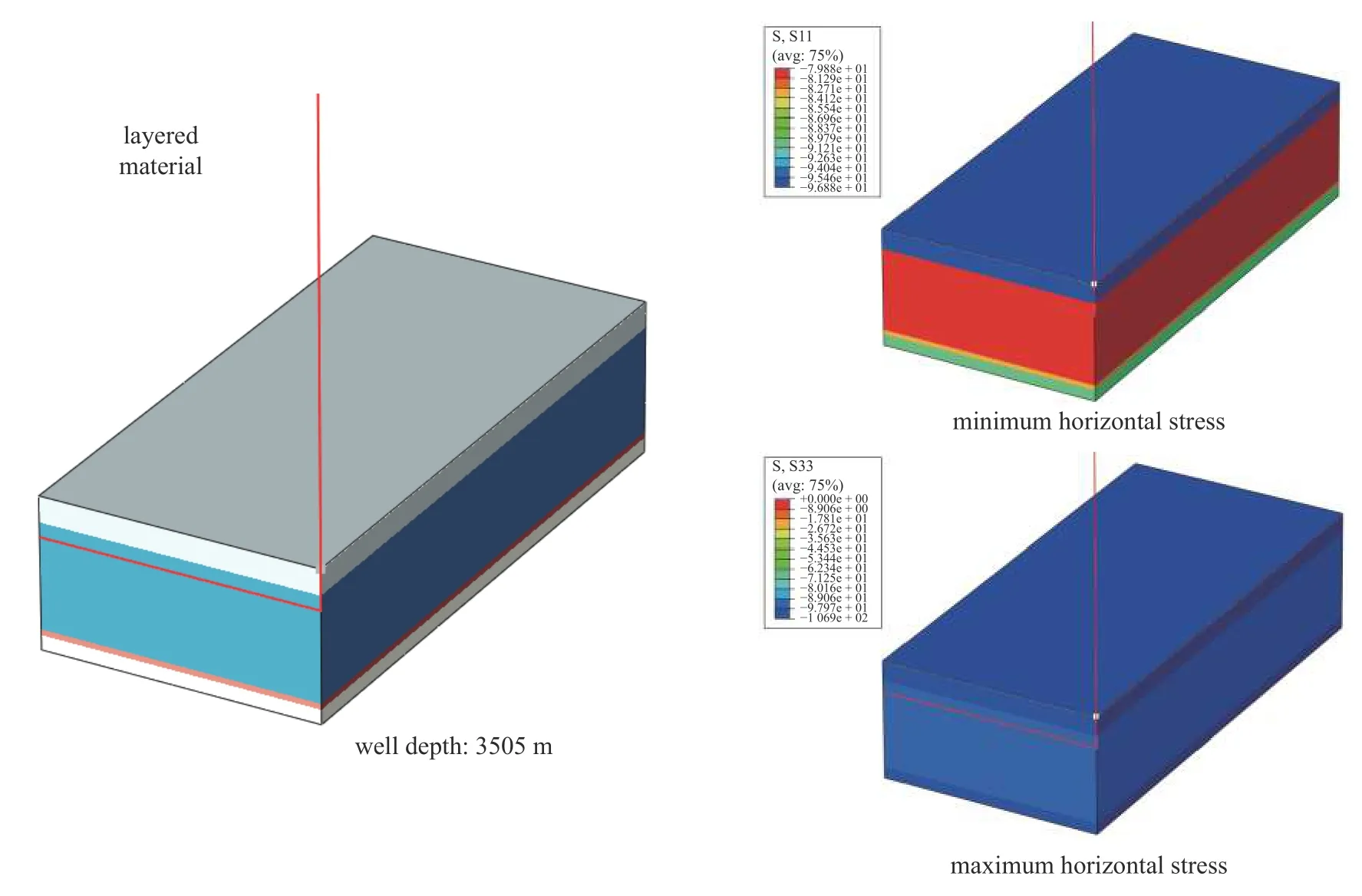
图17 威远204 井水力裂缝扩展模拟的模型示意图(分别为材料分布、最大和最小初始水平地应力的分布),图中的红色线为井筒Fig.17 Diagram of hydraulic fracture propagation simulation model of Weiyuan 204 well (material distribution,maximum and minimum initial horizontal geostress distribution respectively),and the red line in the figure is the bore hole

通过计算模拟,压裂结束后的水力裂缝扩展情况如图18 和图19 所示.这里分别显示了以不同视角观察的结果(只显示裂缝的情况,和包含了地层且将地层沿水平面切割开的情况).从图中可以看出,4 个射孔簇的水力裂缝都扩展了较长的距离,压裂改造效果较好.而在这4 个射孔簇中,两边的两个水力裂缝簇扩展得较长,中间的两条扩展得较短,其主要原因是水力裂缝之间的应力阴影效应引起了水力裂缝的互相屏蔽和干扰,导致从井筒流入4 条水力裂缝簇中的压裂液流量分配不均匀,所以不同的水力裂缝簇扩展的长度和张开的宽度不同.

图18 威远204 井水力裂缝扩展情况模拟结果(这里只显示了水力裂缝,左边和右边分别代表了不同的视角)Fig.18 Simulation results of hydraulic fracture propagation of Weiyuan 204 well (only hydraulic fractures are shown here,and the left and right represent different perspectives respectively)

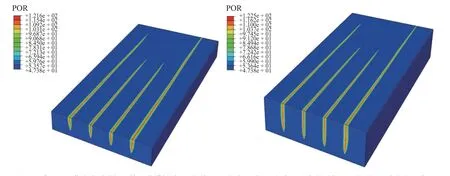
图19 威远204 井水力裂缝扩展情况的模拟结果(整体显示,包含了地层;左边和右边分别表示切分不同深度进行观察)Fig.19 Simulation results of hydraulic fracture propagation of Weiyuan 204 well (overall display,including the formation;the left and right respectively represent the segmentation of different depths for observation)

此外,通过模拟结果可以看出,最长的水力裂缝簇扩展约200 m (第一个射孔簇),最短的水力裂缝簇扩展约150 m (第三个射孔簇),缝口的裂缝高度约为38 m (接近于储层的厚度37 m),最大的裂缝宽度为9.9 mm.且4 条水力裂缝簇都主要在储层内(3499～3536 m)扩展,没有穿出上下盖层,这和预期是一致的,即主要是由储层的最小水平初始地应力控制.储层的最小水平初始地应力比上下两个盖层的最小初始水平地应力小8 MPa 左右,导致水力裂缝内的流体压力较低,无法穿透上下盖层.由于限制了缝高,水力裂缝只能在储层中扩展,使得其可以扩展至更远的距离.通过上述模拟结果提取的数据与实际压裂施工中微地震监测事件所确定的水力裂缝扩展范围也是一致的.

4 数据驱动的页岩气采收率预测

近年来,机器学习在工程和科学的各个领域显示出巨大的应用前景,常被用于解决多维复杂数据的高精度、高鲁棒性表征问题[75-76].对于页岩气开采问题,工程控制参数、地层物性参数多、时空间范围大的特点,适合引入深度学习方法克服传统方法所遇到的困难.目前,在页岩气高效开采中,机器学习模型存在如下潜在应用场景[77]:(1)通过现场施工参数与微地震历史信息,建立基于现场施工场景的深度学习模型,寻找反映地下储层改造情况的关键参数,快速、准确地预测采收率;(2)建立采收率预测的代理模型与页岩气采收仿真系统,通过交互环境,寻找最优压裂参数的最优组合,实现压裂参数的动态优化与调控.针对页岩气压裂现场真实数据量少和各类型参数多的条件[78],本节简要探讨了一种适用于小数据集的机器学习模型—极限梯度爬升(extreme gradient boosting,XGBoost)[79-80],寻找微地震信息、压裂参数与采收率之间的隐式映射关系[81],如图20 所示.

图20 水力压裂现场数据的提取与整理Fig.20 Data extraction and arrangement of fracturing field data

数据集的整理是机器学习的前提,对于采收率预测模型,数据集中的地层改造情况通过微地震信息体现,现场施工情况则通过压裂参数反映.我们对重庆市涪陵焦石区块压裂现场采集数据,包含各类主要微地震、压裂参数信息以及生成记录的水平井数据.目前的数据来自14 口水平井,考虑按射孔簇将每口水平井分为多个压裂段,每个压裂段相对独立,因此可将压裂段作为独立单位,把14 口井的数据进行拆分,达到数据扩容的目的,提高机器学习模型的训练精度与可靠性.如图21 所示,不同颜色的点代表不同的压裂段,作为区分不同压裂段的方式,据此将每口水平井的数据进行分割.经过这些处理,总计可以获得水平井186 个压裂段的各类型数据.由此,我们将各类型数据进行了筛选与整理,根据数据数量和特征,以及预测目标,建立合适的XGBoost模型,进行页岩气采收率的预测.

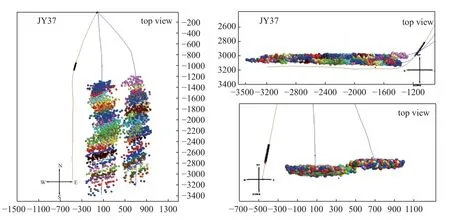
图21 水平井与分段扩容数据Fig.21 Horizontal wells and data expansion

本文对压力、深度等具有物理意义的连续型特征采用标准正态分布的归一化方法,而对于压裂次数、单段类型、穿行层数等离散型的施工参数则通过one-hot 编码[82]完成归一化处理,实现了不同类型特征并存的数据处理与整合.根据筛选统计,在给出的53 个特征中,射孔井段、单段类型和穿行层位为离散型的类别数据,采用one-hot 编码后,分别表示为长度为3,15 和10 的向量,其余50 个特征分别表示为浮点型数据,因此用于XGBoost 模型训练的输入特征变量为78 个,而训练标签为各水平井分段压裂的产气量,表示为单个的浮点值,由此建立了训练数据集.同时,我们保留15 组未用于模型训练的数据,将其用于评估模型的泛化能力.本文所建立的页岩气采收率预测模型的训练流程如图22 所示.使用训练好的模型,可将待预测分段的水平井现场施工数据,以及地层改造信息按相同的形式进行处理,即可对采收率进行预测.

图22 页岩气采收率预测模型训练流程Fig.22 Workflow of prediction model for gas production

图23 给出了XGBoost 预测采收率的结果,由于不同压裂段的产气量数值差异较大,产气量均使用对数坐标表示.图中实际产量用蓝色线段表示,预测产量用棕色线段表示,XGBoost 的最大误差为41.96%,平均误差为14.67%.在本问题样本数据量小的限制下,使用树模型可以给出比较理想的采收率预测.随后期数据的不断收集与整合,通过增加用于模型训练的数据量,可以进一步提升模型预测准确率与泛化性能,实现精准的实时采收率预测.

图23 XGBoost 预测产气量与实际产气量对比Fig.23 The comparison between real and predicted gas production by XGBoost model

值得关注的是,Sun 等[83]同样从现场的压裂曲线和微地震数据中直接挑选出了关键的控制变量,建立合理的显式关系,对地下储层的关键参数以及储层实时压裂特性进行了预测评估.与上述方法相比,深度学习模型则是先对现场数据进行初筛,尽可能保留存在影响的变量,借助深度学习模型可能快速、准确寻找复杂多变量之间映射关系的强大能力,建立复杂的隐式关系,进而挑选出对产气量预测起主导作用的因素.在未来,上述两种方法可进行有机的结合:一方面,对深度学习模型参数按重要性进行排序后,对预测结果起主导作用的施工参数与地层参数若与上述工作理论模型中所使用的物理量保持一致或具有强相关性,则能够对深度学习模型的合理性进行评估.同样地,借助深度学习模型挖掘数据背后复杂关系的能力,找到更多对储层改造和页岩气采收有重要印象的现场因素,进一步发展和完善理论模型.

5 总结

本文研究了页岩气高效开采工程中的钻井完井和水力压裂缝网改造等关键力学问题,得到如下结论.

(1) 页岩是一种典型的非均质各向异性多孔充液弹性介质.固体变形与孔隙流体渗流耦合,采用Biot本构模型,引入孔隙压力和流体体积分数变化量,将整个多孔材料视为一个连续的弹性介质.提出了考虑时间效应的多孔充液弹性本构模型,成功诠释了在土壤与岩石的传统弹性力学中所不能解释的现象.

(2) 页岩的强度与断裂韧性表现出各向异性特征.基于最大应变能释放率准则分析了弱面模型下裂缝的扩展规律,指出裂缝扩展方向仅与当前裂缝方向与弱面方向的夹角和弱面相对强度比值,以及裂缝扩展前的应力强度因子比值三者有关.基于该结论提出裂缝扩展禁止区.

(3) 钻井液的压力控制是井壁稳定性的关键技术难点.基于多孔弹性本构模型,在综合考虑各个时刻及各破坏位置处的应力场与孔隙压力场后,对于各向同性及横观各向同性多孔弹性岩石总结出了八种失效模式下对应的破坏位置、时间效应、以及破坏种类,给出了井壁极限压力解析解,以方便工程直接应用.

(4) 在大多数强度分析情况下,发现广义胡克定律预测的井壁不会发生剪切破坏的结论是偏于不安全的,使用多孔弹性本构进行井眼安全校核是非常必要的.建议在石油工程问题中使用多孔弹性本构模型代替广义胡克定律进行井壁稳定性安全校核.

(5) 数值模拟是研究水平井水力压裂的有效方法,多孔弹性介质中的水力压裂模拟需要耦合岩石的变形与断裂、多孔介质中流体流动和水力裂缝内流体流动的过程.通过模拟威远204 号水平井水力压裂施工过程,给出了一个压裂段内多条射孔簇裂缝同时平行扩展的过程.

(6) 建立了数据驱动的页岩气采收率预测方法,在涪陵焦石区块14 口井小数据样本的前提下,给出了实际产量与预测产量误差小于15%的采收率预测结果.

致谢

衷心感谢黄克智院士对本文研究工作的具体指导,并带领我们投入页岩气高效开采水力压裂和井壁稳定性的研究.感谢中石油勘探开发研究院廊坊分院和中石化江汉油田公司涪陵分公司的技术合作.

附录A

2015年3 月19 日，郑哲敏先生邀请庄茁在中科院力学所做页岩水力压裂报告（赵亚溥摄）

附录B

2017年4 月11 日，郑哲敏先生在中石油勘探院廊坊分院调研页岩大物模水力压裂实验（庄茁摄）