一种双星故障条件下RAIM可用性评估的改进方法
马下平 余科根 贺小星 严 丽 赵立都
1 西安科技大学测绘科学与技术学院,西安市雁塔路58号,710054 2 中国矿业大学环境与测绘学院,江苏省徐州市大学路1号,221116 3 江西理工大学土木与测绘工程学院,江西省赣州市红旗大道86号,341000 4 江西省防震减灾与工程地质灾害探测工程研究中心,南昌市广兰大道418号,330013 5 重庆交通大学土木工程学院,重庆市学府大道66号,400074
BDS是我国自主建设、独立运行的全球卫星导航系统[1-4],可为用户提供更多高定位精度和可靠性的导航信息,同时也可为民用航空接收机自主完好性监测(receiver autonomous integrity monitoring,RAIM)提供有力支撑。RAIM对卫星进行故障监测会受到卫星个数和卫星几何分布的影响。当可见卫星数过少或几何分布不理想时,由卫星几何结构引起的定位误差会遮掩卫星故障引起的定位误差,造成完好性监测结果不可信,漏检率增加。因此在进行故障监测之前必须进行可用性判断,以保证不会影响故障监测性能[5]。RAIM可用性计算中涉及到漏检率和误警率参数,王尔申等[6]研究发现,RAIM可用性随漏检率和误警率的降低而降低。
目前,基于单星故障的RAIM可用性评估方法主要有水平保护法(horizontal protection level method,HPLM)、最大水平精度因子法(δHDOPmax)和近似径向误差保护法(approximate radial-error protection method,ARPM),理论上这3种方法具有等价性[7-8];考虑到2颗卫星同时发生故障的可能性,倪育德等[9]从1颗卫星故障的可用性出发,推导出2颗卫星故障的可用性;针对多故障卫星的可用性,陈金平等[10]提出基于漏检概率和圆概率误差的可用性分析方法。随着GNSS的发展与应用以及飞机更高阶段精密进近的需求,具备垂直导航能力的高级接收机自主完好性监测(advanced RAIM,ARAIM)被引入。ARAIM旨在全球范围内提供垂直导向-200 ft定标性能(LPV-200)级别的航空导航服务,众多学者对此进行了相关算法改进和定位性能方面研究[11-17]。
现有的双星故障条件下RAIM可用性评估大多沿用已有的矩阵最大特征值方法(matrix maximum eigenvalue method,MMEM)[18],该方法可解决2个粗差比值的计算,但该值还可采用高等数学中求极值方法得到。为此,本文提出针对RAIM可用性评估的极大值方法(maxima method,MM),并基于完好性风险参数和IGMAS中8个GNSS站的实测数据对这2种方法的RAIM可用性进行验证,得到最新的中国境内BDS可用性性能。
1 RAIM方法原理
1.1 RAIM观测方程建立
RAIM主要是基于GNSS中的伪距观测量。若在历元t时接收机r与卫星s进行同步观测,并观测m颗卫星,则观测方程可表示为:
y=Hx+ε
(1)
式中,y为m维伪距观测值与近似卫地距的差向量;H为m行4列设计矩阵,表示各卫星对用户的投影向量;x为测站坐标和接收机钟差构成的四维向量,ε为m维观测伪距的误差向量。
给定观测量权阵为P,则式(1)的最小二乘解为:
=x+(HTPH)-1HTPε
(2)
=(I-H(HTPH)-1HTP)ε
(3)
令
(4)
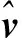
(5)
1.2 检验统计量构建
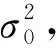
(6)
(7)
一般取检验统计量(T)为:
(8)
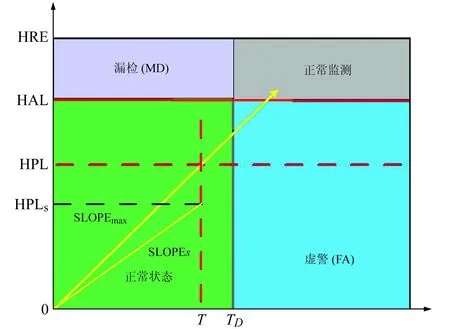
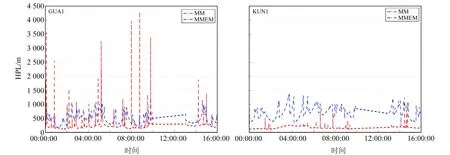
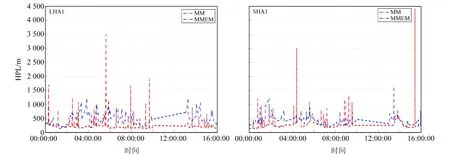
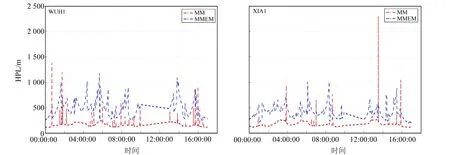
在导航过程中,将实时解算的T值与监测门限(TD)进行比较,TD计算可参考文献[19]。若T 在进行RAIM之前,首先根据性能指标对当前可见星的几何分布进行判断,分析是否适合进行完好性监测,即判断RAIM算法是否可用。 RAIM可用性判断时需要构建T与定位误差之间的数学关系。由于RAIM不具备垂直导航能力,因此本文只讨论水平保护级别(horizontal protection level,HPL)。 图1中横轴表示T,纵轴表示水平径向误差(horizontal radial error,HRE),将这2个变量取比值后得到图中斜线斜率(SLOPE),即 (9) 图1 T与HPL之间的关系Fig.1 The relationship between T and HRE 从图1可以看出,T与HRE呈线性关系,沿此倾斜线,当伪距观测量中存在偏差时,T与HRE线性增加。偏差较小时,HRE小于HPL且T小于TD,系统处于正常状态(图1左下角),PMD较低;偏差较大时,HRE大于HPL且T大于TD,系统能正确监测偏差(图1右上角),PMD也较低;当偏差处于两者之间时,PMD可能达到最大(图1左上角)。对应相同T值时,SLOPE越大,卫星发生故障时MD概率越高。对应卫星的SLOPEs为: (10) 在m个观测量中,HPL可表示为: HPL=max(SLOPEs)·T=SLOPEmax·T (11) RAIM可用性分析就是利用SLOPEs在各历元的最大值SLOPEmax进行判定,依据SLOPEmax求出HPL,并与水平告警限值(horizontal alarm limit,HAL)进行比较,如果HPL 在忽略观测伪距随机误差的情况下,当观测误差ε在第i个和第j个观测值中存在粗差bi和bj时,则有: (12) 根据式(5)可以得到定位解的误差向量为: (13) 则有: (14) 将式(12)代入式(5)可得: (15) (16) 以往对k值主要采用矩阵最大特征值方法(MMEM)[9,18,20]进行求解,但其也可采用高等数学中求极值的方法获取,具体如下: 为求式(16)的极大值,两边取对数,并对式中k求偏导,可得一元二次方程式: ak2+bk+c=0 (17) 设k1和k2分别为式(17)两根,将k1、k2分别代入式(16),则当前历元的(SLOPEij)max可表示为: (SLOPEij)max= max((SLOPEij)k1,(SLOPEij)k2) (18) 即可得到双星故障时的HPL为[19]: (19) 目前求解HPL主要采用MMEM方法,该方法主要是构建关于粗差向量b的二次型矩阵,根据矩阵的最大值为矩阵最大特征值这一定律求解HPL,具体计算过程可参考文献[18]。 实验数据采用国际GNSS监测评估系统(international GNSS monitoring and assessment system,IGMAS)提供的中国境内BJF1、CHU1、GUA1、KUN1、LHA1、SHA1、WUH1、XIA1共8个连续跟踪站2020-09-06的观测数据和星历文件。通过自编程序统计这些测站在截止高度角5°以上的BDS卫星可见性、DOP值和基于2种方法的双星故障HPL值,比较并分析中国境内BDS可用性和2种双星故障RAIM可用性的差异。具体数据情况及处理策略为:1)BJF1和CHU1站观测时段为00:00:00~09:59:30;GUA1、KUN1、LHA1、SHA1站观测时段为00:00:00~15:59:30;WUH1和XIA1站观测时段为00:00:00~16:59:30;2)考虑到每个测站不完全包含双频或三频观测值,因此采用BDS B1I频率的单频观测值;3)全球星历文件中每隔1 h给出用于计算每个历元的BDS卫星轨道参数、卫星钟差参数和卫星状态信息,其1 d的全球星历文件可从MGEX网站下载;4)电离层延迟采用Klobuchar模型进行改正,对流层延迟采用Saastamoinen模型进行改正;5)式(2)中P采用已知的高度角定权法[21],定权时考虑3种异构卫星之间的差异,将GEO和IGSO+MEO卫星的权比关系设置为1∶5[22]。 利用8个IGMAS站的BDS观测数据和全球星历文件,计算出每个测站每个历元对应卫星的高度角,并统计可见卫星数、平均卫星数、GDOP值及其平均值。结果表明:1)中国境内8个IGMAS站的BDS可见卫星数最小值为17颗,完全能够满足RAIM可用性评估;2)GDOP最小值、平均值和最大值的均值分别为1.117、1.437、2.186,说明BDS卫星在中国境内空间分布情况很好。 目前BDS在中国区域的定位精度为5m左右[4]。保守起见,将σ0设置为8 m,PMD设置为10-3,PFA设置为10-5[19]。利用2种方法分别计算BDS双星故障时HPL值,图2~5分别为8个IGMAS站的HPL坐标时间序列,表1(单位m) 图2 双星故障条件下BJF1和CHU1站HPL时间序列Fig.2 HPL time series of BJF1 and CHU1 stations under double-satellite faults conditions 图3 双星故障条件下GUA1和KUN1站HPL时间序列Fig.3 HPL time series of GUA1 and KUN1 stations under double-satellite faults conditions 图4 双星故障条件下LHA1和SHA1站 HPL时间序列Fig.4 HPL time series of LHA1 and SHA1 stations under double-satellite faults conditions 图5 双星故障条件下WUH1和XIA1站HPL时间序列Fig.5 HPL time series of WUH1 and XIA1 stations under double-satellite faults conditions 表1 2种方法计算的HPL值统计 为8个IGMAS站的HPL最小值、最大值和平均值。通过分析可知: 1)从整体上看,MMEM计算的HPL小于MM计算的HPL,表明MMEM得到的RAIM可用性高。利用MM求解的8个IGMAS站的HPL最小值、平均值、最大值的均值分别为124.921 m、233.141m、3 020.005 m;MMEM求解的HPL最小值、平均值和最大值的均值分别为219.093 m、515.110 m、1 302.518 m。 2)2种方法得到的HPL时间序列中,大部分历元的HPL值一致性很好,HPL平均值的差值约为281.969 m,主要原因可能为这2种方法的计算公式中所用参数个数和精度存在差异。 3)在中国区域,双星故障条件下HPL值的空间分布存在差异,表明RAIM可用性与地理位置相关。 表2(单位s)为2种方法的计算时间,从表中可以看出,MM和MMEM的平均计算时间分别为11.733 s和21.387 s,MM比MMEM计算时间短。 飞机在飞行阶段包含非精密进近(non-precision approach,NPA)、终端、本土航路和远洋航路4个飞行阶段[23],4个阶段的HAL值分别为555.6 m、1 852 m、5 556 m和7 408 m。基于2种方法得到双星故障条件下HPL值,根据每个测站计算出观测历元中各阶段的可用性百分比,再计算8个测站的可用性比值均值,得到每个阶段的可用性结果(表3)。从表中可以看出:1)MM计算的可用性在航路和远洋阶段达到100%,而MMEM计算的RAIM可用性除在NPA阶段外,其他阶段的可用性均达到100%;2)结合所计算的HPL值,虽然MMEM在NPA阶段的可用性不及MM,但整体上MMEM可用性优于MM。 表2 2种方法的计算时间比较 表3 单星和双星故障条件下RAIM可用性统计 本文从双星存在故障的前提条件出发,在总结已有的最大特征值计算RAIM可用性方法的基础上,提出RAIM可用性评估的极大值方法,并以2020-09-06中国区域8个IGMAS连续跟踪站的BDS观测数据为例,比较和分析中国境内HPL变化及RAIM可用性情况,得到以下结论: 1)中国境内可见卫星数和GDOP完全能够满足可用性计算需求,中国境内BDS目前至少可观测到17颗可见卫星,GDOP值最大为2.186,可为RAIM可用性计算和故障监测提供丰富的数据源。 2)虽然MM计算的RAIM可用性在NPA阶段高于MMEM,且耗时较少,但总体来说,MMEM计算HPL的时间序列小于MM,即对应的RAIM可用性更高。 3)2种方法计算的HPL存在差异,主要原因可能为各方法所用参数个数及本身精度存在差异,且RAIM可用性计算中涉及到完好性风险参数,不同的参数初值会对RAIM可用性评估产生不同影响,因此参数取值应引起重视。2 RAIM可用性分析方法
2.1 监测统计量与定位误差的关系
2.2 双星故障时MM求解HPL
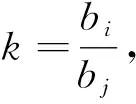
2.3 双星故障时MMEM求解HPL
3 数据处理
3.1 实验数据和处理策略
3.2 卫星可见数和DOP值
3.3 2种方法计算双星故障时HPL比较


3.4 计算时间比较
3.5 2种方法双星故障时可用性统计


4 结 语

