开放空间H2/CH4/空气爆炸实验与数值模拟研究1)
崔洋洋 王 成 钱琛庚 谷恭天 高 扬
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
引言
近年来氢燃料的使用范围逐渐发展到多个领域,如氢能源汽车,氢燃料电池等,加氢站等相对开放的涉氢场所也逐渐增多,未来车辆充能站可能同时具备加油、加气(氢气、甲烷)等功能,该场所一旦发生泄漏后,多种可燃气体与空气混合形成可燃气云,可发生燃爆事故,造成严重的人员伤亡和财产损失[1].目前对于开放空间气体爆炸的实验研究,主要是采用肥皂泡、聚乙烯薄膜等弱约束来形成不同形状的气体云,主要形状包括球形、半球形和圆盘形.Thomas 等[2]首先使用肥皂泡作为弱约束开展了无约束气体爆燃的研究.Kim 等[3]研究了氢气火焰传播行为,并使用肥皂泡法测量了氢气-空气混合物在开放空间意外爆炸产生的冲击波强度,但是由于肥皂泡尺寸的限制,并未能对火焰传播特性进行完全描述.Kim 等[4]发现,塑料薄膜是一种能够替代肥皂泡的气体约束材料,它能包裹体积较大的气体且对爆炸反应影响不大.Otsuka 等[5]通过乳胶气球来限制氢气进行了火焰传播特性研究,基于稳定火焰传播理论,通过高速摄影图像分析了压力与火焰速度的关系.
对于真实的气体意外爆炸事故,火焰的传播一般都会受到障碍物的限制.国内外相关学者针对障碍物环境下气体爆炸的火焰传播规律和超压特性进行了大量研究.文献[6-8]建立了具有不同结构的障碍物,研究了甲烷和乙烯等易燃易爆气体的火焰传播特性,发现在障碍物的干扰下,火焰的传播速度和超压均显著提高.众多研究表明[7-8],障碍物引起的湍流提高了气体火焰燃烧效率,进而显著提高了火焰的燃烧速度.Masri 等[6]通过实验研究了障碍物横截面形状对于火焰加速的影响,结果表明方形截面的障碍物能够导致更强的火焰加速效应.Dorofeev[9]首次在计算模型中考虑了障碍物的结构尺寸,并通过研究发现由于火焰自身不稳定性引起的火焰速度增加量远低于由于障碍物湍流作用导致火焰速度增加量.Hall 等[10]研究了固体障碍物的数量和位置对于湍流预混火焰传播速率的影响,结果表明:随着障碍物面积的增加,超压峰值会先增加到一个阈值后逐渐降低;同时当障碍物堆叠较近时,会得到更高的超压.Chen 等[11]通过实验和基于火焰表明密度模型的大涡模拟数值模拟研究了阻塞比(BR)对于火焰加速过程的影响,发现火焰头部传播速度和压力增长速率随着阻塞比的增加而增大.高伟等[12]建立了更为复杂的包含90 根不锈钢管的框架障碍物模型,通过实验和数值模拟手段进行了障碍物对于天然气爆炸特性的影响研究,得到了与Dorofeev 研究相同的结论.
随着数值计算的发展,使得复杂结构下气体爆炸传播特性的研究成为了可能.张强等[13]开展了戊烷云团在甲类仓库中的爆炸特性数值仿真研究,分析了不同点火位置、物资体积和不同燃料浓度对爆炸超压的影响,确定了针对上述因素的最危险爆炸场景.闫秋实等[14]通过数值仿真方法得到了住宅内燃气爆炸产生的冲击波云图,并研究了燃气体积和浓度对于爆炸超压的影响.Davis 等[15]通过实验和数值仿真手段,对大尺度环境下(1500 m3)的甲烷和丙烷爆燃进行了研究,分析了不同几何布局的障碍物对于火焰传播速度和超压的影响.李静媛等[16]基于FLACS 软件建立了加氢站简化几何模型,并对氢气意外爆炸进行了数值模拟,研究了环境障碍系数和环境风速对氢气爆炸火焰传播特性的影响.进一步地,为了研究真实环境下气体爆炸的火焰传播规律与超压分布特性,需要建立更为真实且复杂的结构模型,这意味着需要更加高效的数值计算方法.大涡模拟(LES)作为描述湍流运动的新兴手段,是目前研究湍流问题的主流数值仿真方法,可以精准快速而无需占用太大计算机内存分析复杂的湍流流场,适用于大尺度开放环境下的气体爆炸研究[17].文献[18-20]利用LES 模拟研究了管道、容器内气体爆炸传播规律,发现数值模拟结果与实验结果吻合较好.目前对于气体爆炸事故大多集中在小尺度的实验或数值模拟研究,且对双组份燃料混合气体的研究较少;障碍物的设置过度简化,与实际工况相差较远;危险化学品爆炸过程呈现高度的非定常和非理想特性,爆炸在传播过程中存在强烈的几何边界、化学反应等因素的相互作用,现有数值模拟精度较低,难以应用于实际场景的气体爆炸的预测与评估.
本文采用氢气、甲烷两种常见能源为研究对象,研究了氢气-甲烷-空气混合气体在开放空间爆炸的时空演化规律,给出了氢摩尔分数、混合物当量比、混合气体云团尺寸、障碍物约束等对爆炸传播的影响,建立了考虑氢摩尔分数、混合物当量比、混合气体云团尺寸的最大爆炸超压TNT 当量预测方法及爆炸火球自加速火球半径预测方法.利用自主研发的大规模高精度数值仿真模拟软件,给出了建筑物结构对加气站内混合气体爆炸的影响机制,以期为氢气、天然气等能源的安全使用提供参考数据.
1 实验装置
构建了室外开放空间混合气体爆炸测试实验系统(图1),主要包括配气装置、可燃气体约束装置、点火装置(10 J)、压力传感器(Kistler 6233A 系列铅笔型自由场传感器)、数据采集仪(Elsys TranNET 408 DP).采用聚乙烯薄膜作为可燃气云的弱约束物,定制了不同尺寸(L=1 m,1.6 m,2 m)的钢骨架作为聚乙烯薄膜的支撑物.在距离可燃气云中心不同位置处(4 m(P1),5.5 m(P2),7 m(P3),8.5 m(P4),10 m(P5))布置5 个压力传感器.
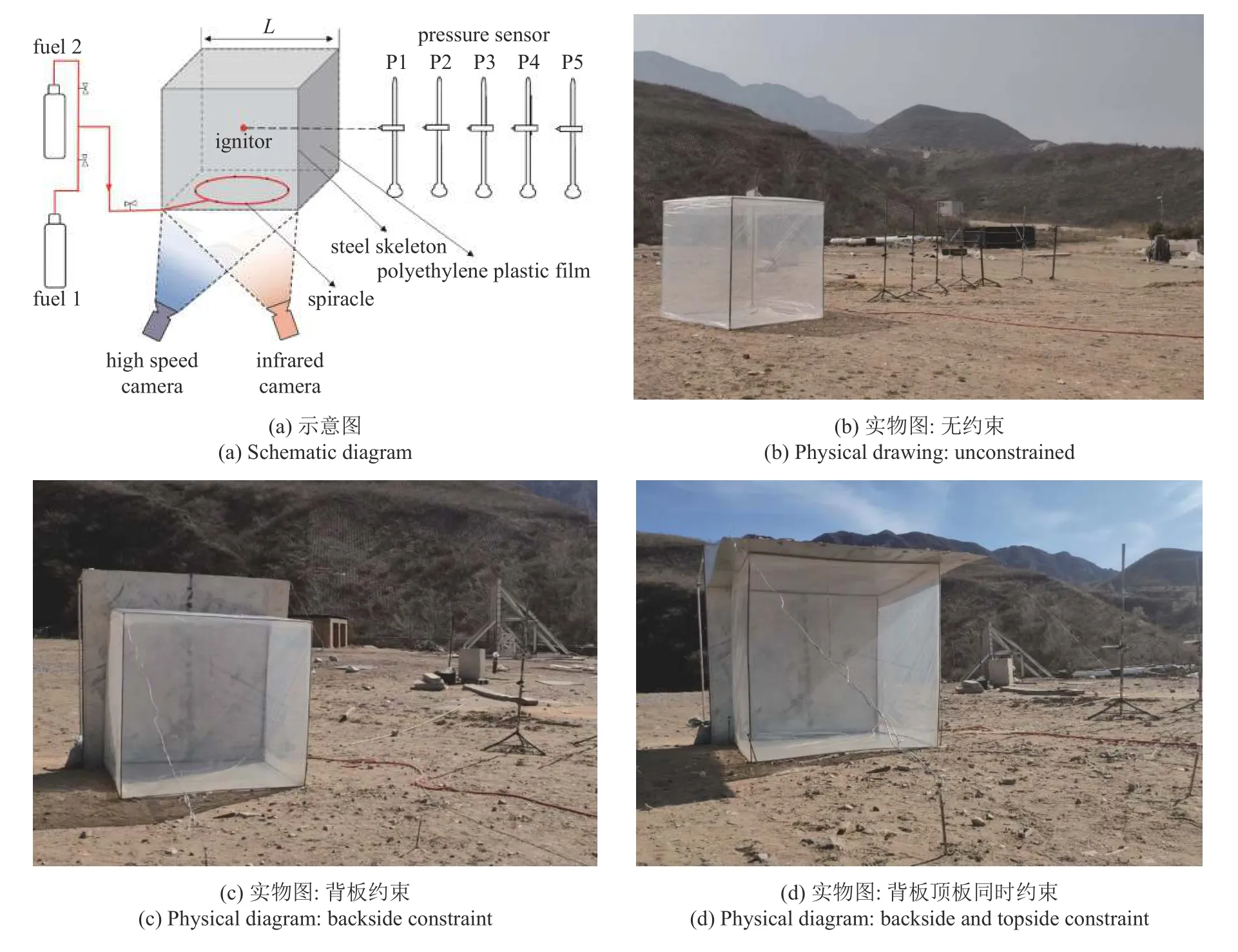
图1 开场空间爆炸实验系统Fig.1 Opening space explosion experiment system
本文采用的对象为氢气-甲烷-空气混合气体,本研究采用氢气与甲烷的混合物为主要燃料,其具体反应如下[21-23]
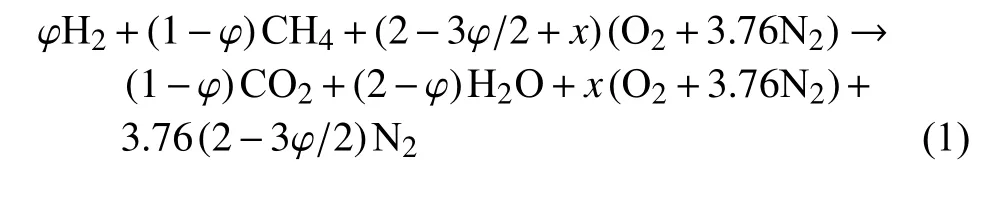
其中,x是过量空气参数;φ 是燃料中氢摩尔分数,可以表示为

2 控制方程与数值计算方法
本文的数值模拟工作采用课题组自主开发的危险化学品爆炸大规模高精度仿真软件完成.该软件基于多组分反应流Navier-Stokes 方程组,通过过滤器过滤,得到LES 控制方程,张量形式的控制方程如下
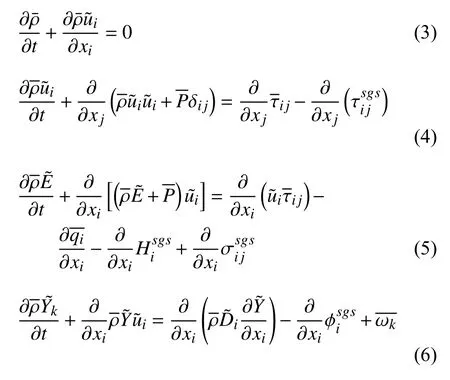

对于亚格子尺度黏性应力,使用Smagorinsky 模型封闭,可以表示为

其中,νt表示亚格子尺度黏性系数

式中,Δ=2Δx是过滤尺度,模型参数Cs,CI是常数,取为0.18,0.0066[24].对于亚格子尺度热通量和组分对流通量采用梯度扩散模型封闭
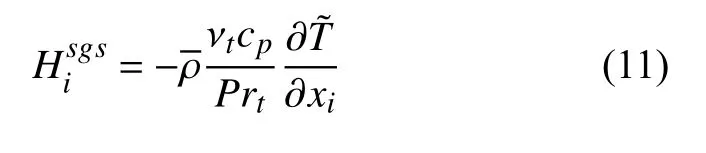
其中Prt=0.75 为亚格子Prandtl 数[24].
化学反应源项使用增厚火焰模型模化,组分守恒方程可以重写为
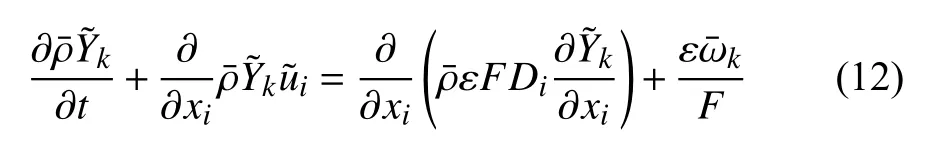
其中F为增厚因子,表示火焰面增厚的倍数,增厚因子可以保证火焰面厚度始终为 8 Δx~10Δx.ε 为效率函数,其作用是为了弥补当火焰面增厚之后火焰面对褶皱变形不敏感的缺陷,本文采用幂律分布表达式[25]

在数值方法中,对流项离散使用五阶WENO 有限差分格式[26],非线性扩散项使用四阶中心差分格式,时间离散采用三阶TVD Runge-Kutta 方法[27].
3 结果与分析
3.1 氢摩尔分数对混合气体爆炸传播的影响
本小节采用的氢气/甲烷/空气混合体系的混合物当量比均为1,可燃云团体积为4 m3.通过改变氢气和甲烷的比例,实现体系中氢摩尔分数的改变,从而研究氢摩尔分数对氢气/甲烷/空气混合气体爆炸的影响.具体实验方案如表1 所示.
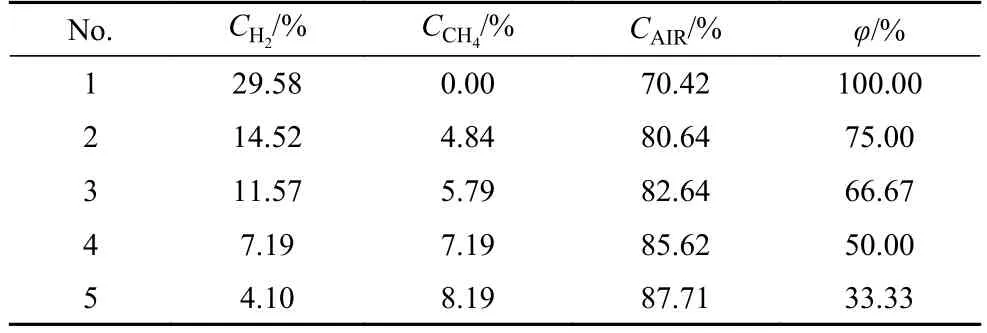
表1 不同氢摩尔分数实验工况Table 1 Experimental conditions for the effect of hydrogen mole fractions
图2 为氢摩尔分数对各位置处爆炸超压的影响.4 m 位置处,氢摩尔分数为100%时,爆炸超压在87.01 ms 时到达最大值,最大爆炸超压为1.84 kPa.氢摩尔分数为75%,66.67%,50%,33.33%时,最大爆炸超压分别为1.09 kPa,0.66 kPa,0.39 kPa,0.32 kPa.可以看出,在各位置处,随着氢摩尔分数的减小,最大爆炸超压逐渐减小,且到达最大爆炸超压的时间逐步增加.换句话说,氢气可以增加氢气-甲烷-空气混合体系的反应活性,使得系统反应更加迅速,且可以增强混合气体的爆炸强度.
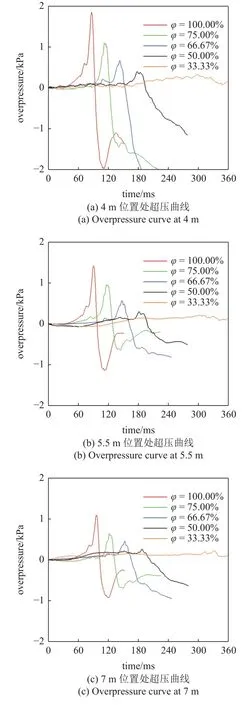

图2 氢摩尔分数对各位置处爆炸超压的影响Fig.2 Effect of hydrogen mole fraction on explosion overpressure at different positions
为了更好地预测氢气/甲烷/空气混合气体爆炸超压传播规律,此处引入TNT 当量法[28-29].TNT 当量法是将可燃气体等同于当量质量的TNT 的一种简单方法.该方法建立在假设燃料爆炸的行为如同具有相等能量的TNT 爆炸的基础之上预测爆炸源周围不同位置处的爆炸超压.TNT 的当量质量可由下式进行估算
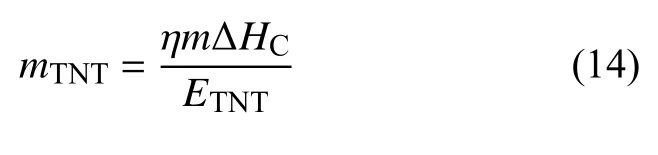
其中,η 为爆炸效率;m为可燃气体的质量;ΔHC为可燃气体的爆炸能/燃烧热(氢气燃烧热:142351 kJ/kg,甲烷燃烧热:55900 kJ/kg);ETNT为TNT 的爆炸能(典型值为4686 kJ/kg).爆炸效率是一个严重依赖经验的数据,根据事故统计结果,可燃气云的爆炸效率在1%~10%之间变化.
已知TNT 当量后,爆炸超压可由下式计算
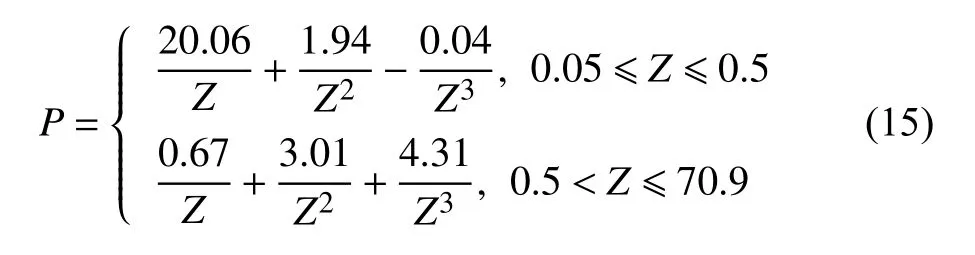
其中,Z=R/mTNT1/3为比例距离,R为测点与爆心之间的距离.
根据此方法,计算了本小节工况2 条件下不同位置处的最大爆炸超压(如图3),由于本小节研究中爆炸周围无障碍物及密闭空间的影响,因此 η 取现有统计值中的最小值(1%).可以看出,距离爆炸中心点4 m 处最大爆炸超压约为7.57 kPa,5.5 m,7 m,8.5 m,10 m 位置处的压力分别下降至5.04 kPa,3.77 kPa,3.00 kPa,2.49 kPa.通过计算得出的数据约为实验测得数据的5~7 倍,因此TNT 当量法中事故统计得出的 η 用于理论研究时会造成很大的偏差.因此针对实验工况条件对理论方法中的 η 进行修正,发现当 η 取0.0085%时,理论计算结果与实验数据吻合较好.此数据远小于事故统计的经验数值.其主要原因在于:(1) 实际爆炸过程中,爆炸源的存储状态、周围建构筑物复杂多变,复杂场景增强了其爆炸强度,有些爆炸还混有扬起的粉尘,因此,η 的估值会偏大;(2)事故统计数据来源于大规模事故报告,爆炸效率可能受爆炸源体积大小等因素影响.
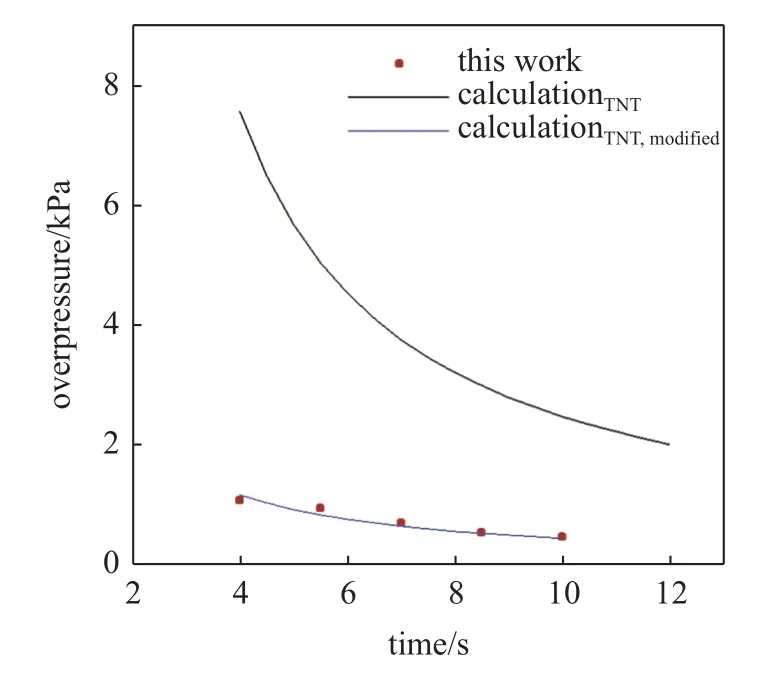
图3 修正后的TNT 当量法计算比对结果Fig.3 Comparison between the result of modified TNT equivalent method and experiment
应用此方法,对本小节其余4 种工况进行修正,得到其爆炸效率分别为0.031%,0.0022%,0.0004%,0.00025%.采用幂函数对其进行理论建模,得到了氢摩尔分数对爆炸效率的影响的理论模型
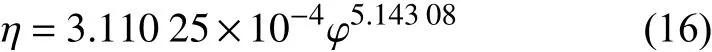
图4 为氢气/甲烷/空气混合气体爆炸火焰扩展过程.图4(a)为高速摄像机拍摄的爆炸传播过程,即使混合气体中掺杂有部分甲烷,后期火焰传播过程中,室外环境仍然难以通过高速摄像机捕捉到完整的爆炸火焰.因此引入高速红外摄像机获取爆炸火焰扩展过程,如图4(b).

图4 混合气体爆炸火球扩展过程Fig.4 Fireball expansion process of mixed gas explosion
图5 为氢摩尔分数对爆炸火球扩展过程的影响.当系统燃料只有氢气时(图5(a)),爆炸火球火焰面较为平整,随着时间的发展,底部火焰发展逐渐减小,而其他三个方向的火焰面发展略快.与其他四个工况相比,火焰面间隔时间 Δt最短(1.2 ms),但相邻两火焰面的位移较大,这说明此工况条件下,爆炸火焰传播速度最快.随着系统内甲烷的逐渐加入(图5(b)~图5(e)),在火焰面间隔 Δt不断增大(1.6 ms,2.0 ms,5.0 ms)的前提下,相邻火焰面的位移逐渐减小,这表明火焰传播速度随着甲烷的加入逐渐减小.同时可以发现,当加入少量甲烷时(图5(b)),火焰面最平滑.随着燃料中氢气减少、甲烷增多,火焰面的光滑程度逐渐降低,出现更多的褶皱.Li 等[30]研究表明爆炸火焰形态受Lewis 数的影响较大,5 种氢摩尔分数混合物的有效Lewis 数均小于1,此时热扩散不稳定性与水力学不稳定性互相增强,火焰面产生褶皱.而随着甲烷的加入,火焰传播速度变慢,不稳定性发展时间增长,使得火焰面产生更多的褶皱.
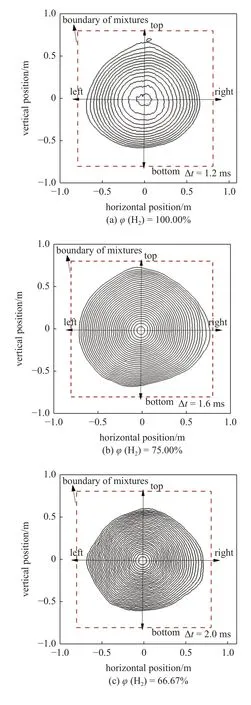
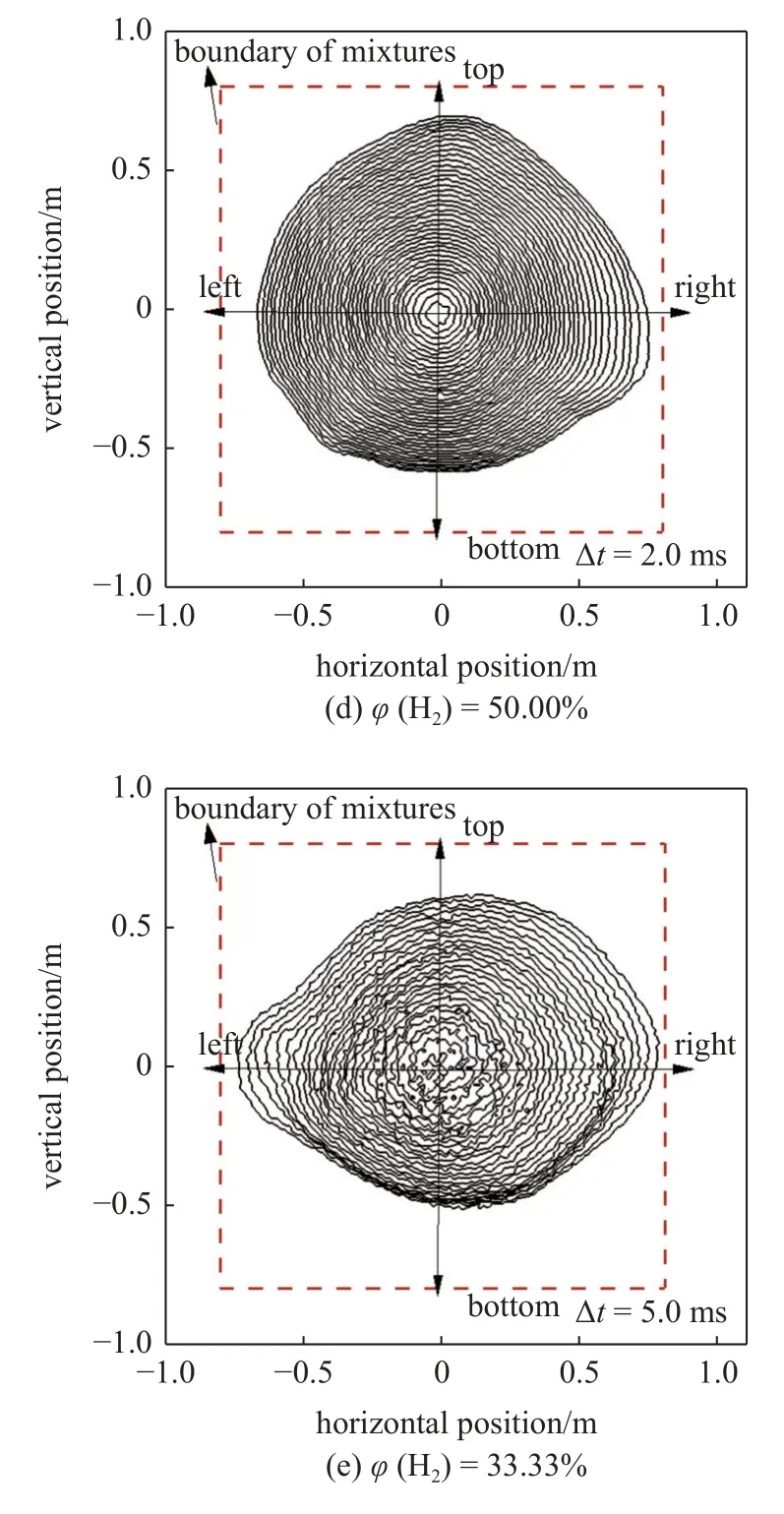
图5 氢摩尔分数对爆炸火球扩展过程的影响Fig.5 Effect of hydrogen mole fraction on explosion fireball expansion process
以图5(b)为分析对象,分别计算得出了爆炸火球传播过程中上下左右四个方向的火球半径,如图6所示,由于地面是刚性壁面,火焰在传播过程中受阻,因此图6 中混合气体爆炸火焰在自由场中传播的平均半径取自于爆炸火球上半圆周的平均半径(左、右、上三个方向的平均半径).
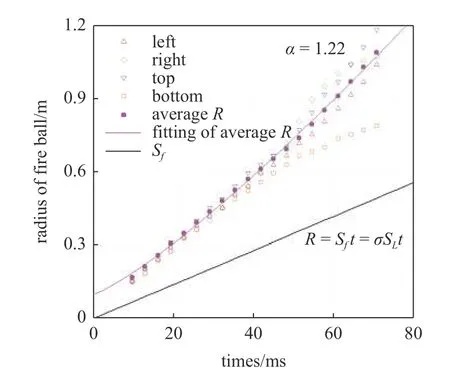
图6 混合气体爆炸火球半径随时间变化规律Fig.6 Variation of fireball radius of mixed gas explosion with time
从图6 中可以看出,当火球较小时,四个方向的半径几乎一致,随着时间的发展,当火球半径达到0.6 m 左右时,各方向的半径开始出现差异,底部方向的半径增长明显减缓,而其他三个方向的火球半径的增长幅度较大.70.4 ms 时,底边半径约为0.79 m,几乎到达地面,而左、右、上三个方向的爆炸火球半径远大于底边半径,分别为1.040 m,1.076 m 以及1.182 m,平均半径为1.091 m,约为底边半径的1.4 倍.这主要是因为地面可以看成刚性壁面,存在明显的压力反射现象,这会大大减缓爆炸火焰的传播,且底边火球的极限半径约为0.8 m,而其他三个方向的传播不会受到刚性地面的约束作用,爆炸火球半径增幅逐渐增大,呈指数增长.这也是本研究中平均速度采用左右上三个方向的平均速度的原因.
层流燃烧火球扩展速度的计算方法为[31]

忽略火焰不稳定性,球形火焰面扩展速度与层流火焰速度的关系为
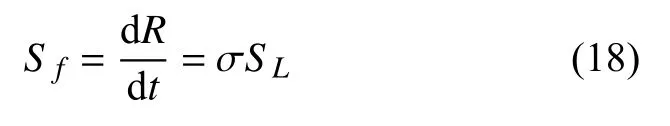
其中,R为层流燃烧火球半径;t为时间;σ 为热膨胀比(未燃气体密度 ρu与已燃产物密度 ρb的比值);SL为层流火焰速度(97.99 cm/s),根据火焰传播扩散理论,层流火焰传播速度可由下式计算得出[31]

其中,pi是化学平衡时第i种自由基的分压;Di,0为第i种自由基在未燃初温时的质量扩散系数;ki为第i种自由基的消耗率常数;cr是反应物的浓度;Xp是产物的摩尔分数;是反应区中气体质量扩散系数、动力学参数和层流火焰速度函数.本小节采用Petrova 等[32]给出的化学反应机理计算得出.
此时,可以看出,爆炸火球扩展速度远大于层流燃烧速度.与层流燃烧火球扩展速度相比,爆炸火球在初始阶段的扩展速度与计算得出的层流燃烧火球扩展速度相差不大.点火后50 ms 左右开始,爆炸火球扩展速度越来越大,远大于层流燃烧火球扩展速度.爆炸火球的传播呈指数增长,已有研究给出了可以描述爆炸火球半径和火焰面传播速度的理论模型[33-37]

其中,R为爆炸火球半径;R0为自湍流临界火焰半径;α为火焰自加速指数.可以得出此种工况下自加速指数 α 为1.22.
图7 给出了五种不同氢摩尔分数条件下的平均火焰半径.火焰自加速指数 α 分别为1.40,1.22,1.14,1.08,1.03,可以看出,氢摩尔分数越大,火焰自加速指数越大,爆炸火焰传播速度越快.
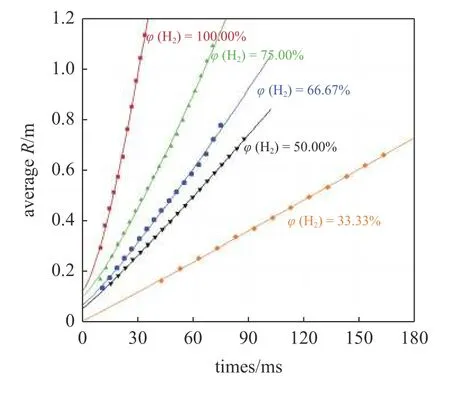
图7 不同氢摩尔分数条件下的平均火焰半径Fig.7 Average radius of fire ball under different hydrogen mole fractions
通过分析可以发现,火焰自加速指数随氢摩尔分数变化规律满足Boltzmann 函数,即

其中,A1为曲线上限值,A2为曲线下限值,φ0为α=A1+A2/2 时对应的x值,且在x0位置处的导数dα/dφ 为 (A1-A2)/(4ω),各参数均为无量纲参数.通过拟合参数A1,A2,φ0,ω 的值分别为1.4,1,71.73,11.75.因此火焰自加速指数随氢气摩尔分数的变化可用下式表示
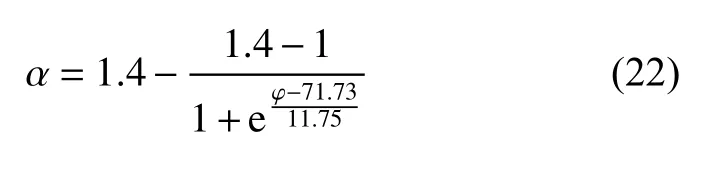
此时,考虑氢摩尔分数影响的爆炸火球半径可通过下式计算
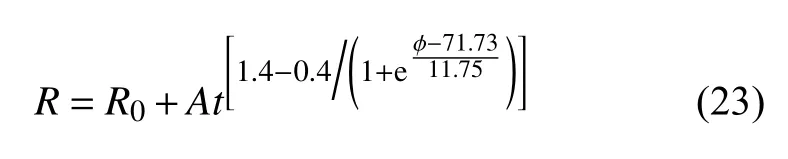
3.2 混合气体当量比对爆炸传播的影响
本小节采用的氢气/甲烷/空气混合体系的氢气摩尔分数为75%,可燃云团体积为4 m3.通过改变燃料与空气的比例,研究混合可燃气体当量比对氢气/甲烷/空气混合气体爆炸的影响.具体实验方案如表2所示.
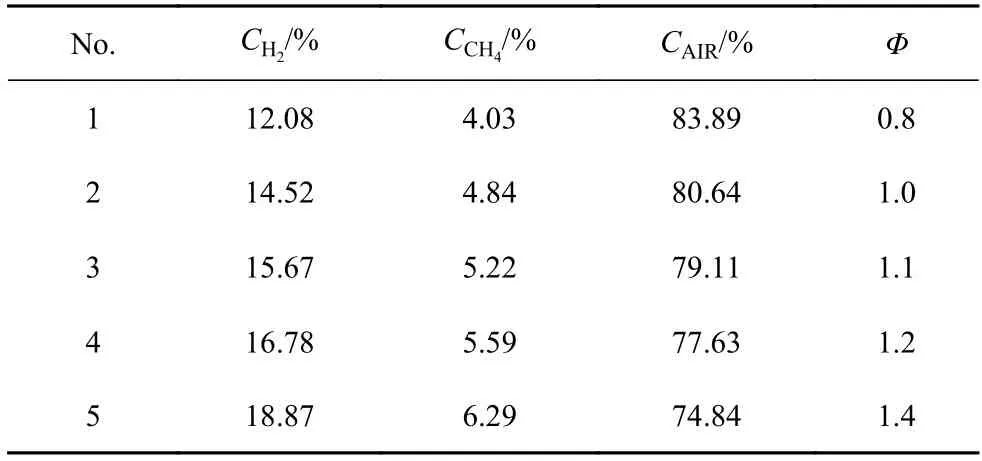
表2 不同当量比实验工况Table 2 Experimental conditions for the effect of equivalence ratio
图8 为当量比对氢气-甲烷-空气混合气体最大爆炸超压的影响.最大爆炸超压发生在当量比为1.1 时,此时,4 m,5.5 m,7 m,8.5 m,10 m 位置处的最大爆炸超压分别为1.364 kPa,1.261 kPa,0.954 kPa,0.771 kPa 及0.530 kPa.与当量比为1.1 时相比,当量比为0.8 时不同位置处的最大爆炸超压分别降低了67.49%,66.24%,62.16,%,55.52%和48.00%,而当量比为1.4 时分别下降了39.24%,40.17%,39.30%,35.06%和37.52%.可以看出,燃料不足时,混合气体爆炸最大压力下降较多.燃料富余时,最大爆炸超压下降程度较小.
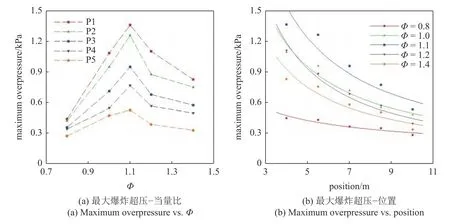
图8 当量比对混合气体最大爆炸超压的影响Fig.8 Effect of equivalence ratio on maximum explosion pressure of mixed gas
图9 为混合气体当量比不同时氢气-甲烷-空气混合气体爆炸火球锋面发展图.可以看出当量比为0.8 时,火焰面较为密集.当量条件下(Φ=1.0)的火焰面比当量比为1.1 和1.2 时火焰面更为密集,此条件下火焰传播并不是最快的.火焰传播最快的工况可能发生在当量比略大于Φ=1.0 时.
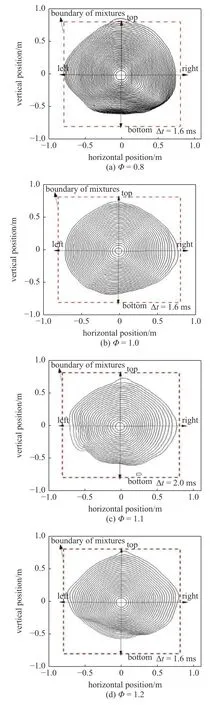
图9 混合气体当量比对爆炸火焰锋面的影响Fig.9 Effect of equivalence ratio of mixed gas on explosion flame front
图10 给出了不同混合气体当量比条件下的爆炸火球半径随时间的变化规律.5 种工况下的火焰自加速指数 α 分别为1.17,1.22,1.23,1.24,1.23.可以看出,火焰自加速指数随着当量比的增大先增大后减小,峰值发生在当量比为1.2 左右,根据当量比Φ与自加速指数 α 的关系,采用GaussAmp 模型进行拟合,自加速指数 α 与当量比Φ的关系为
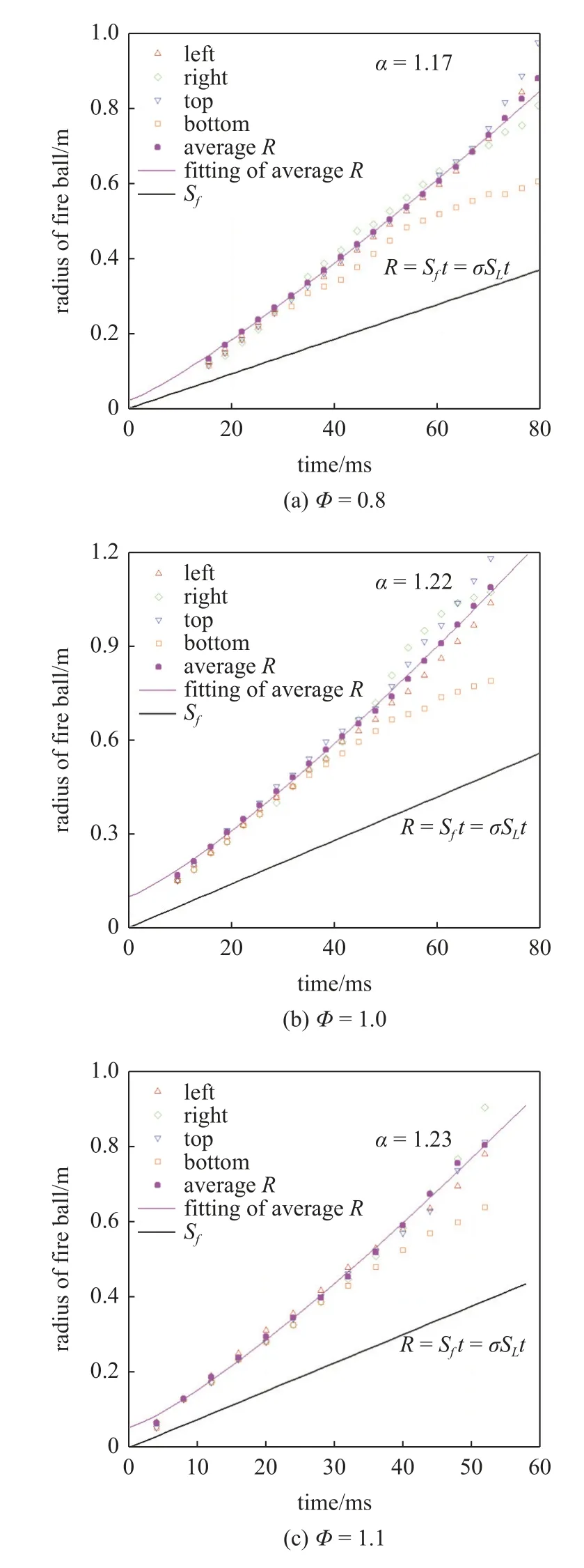
图10 混合气体当量比对爆炸火球半径的影响Fig.10 Effect of equivalence ratio of mixed gas on explosion fireball radius
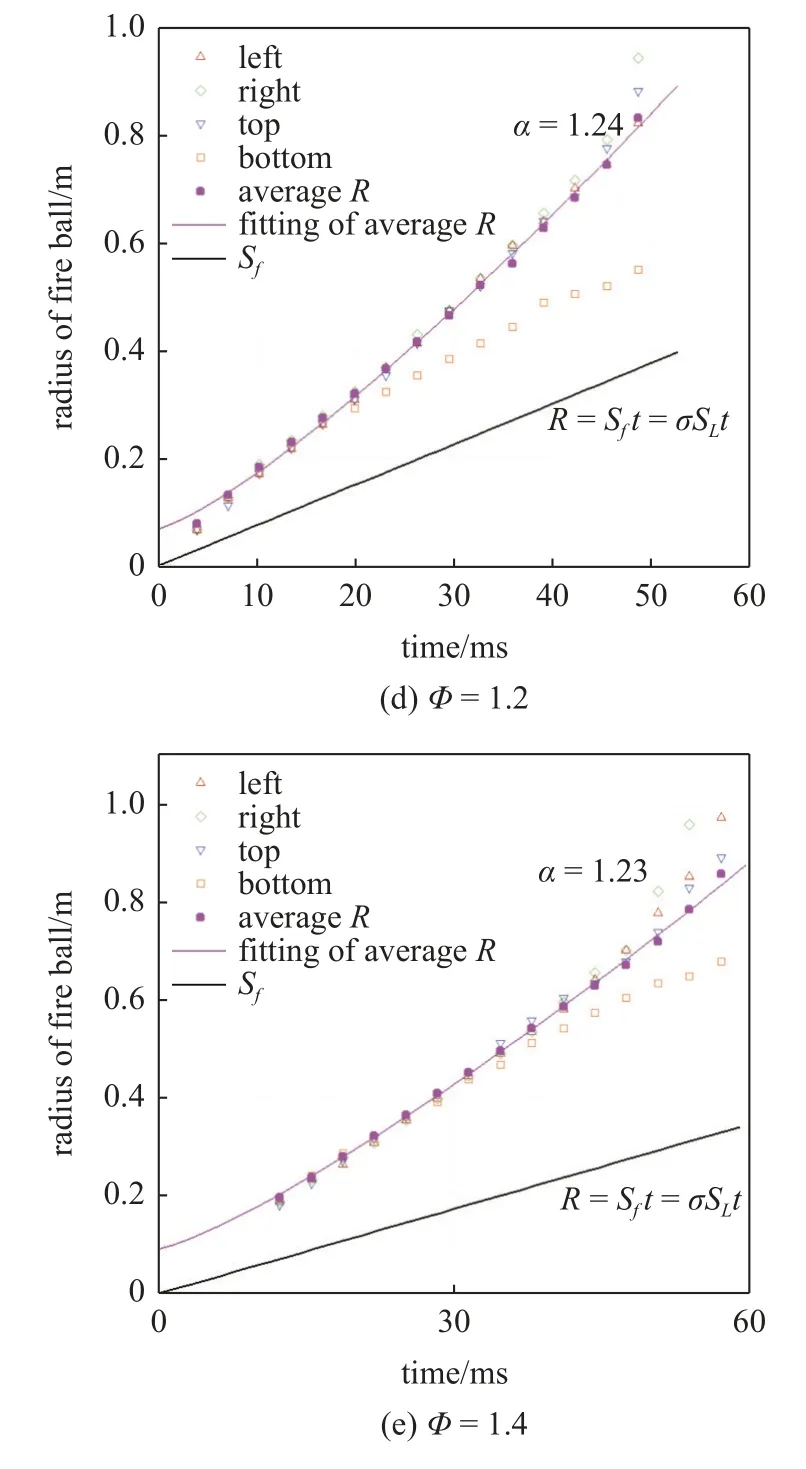
图10 混合气体当量比对爆炸火球半径的影响 (续)Fig.10 Effect of equivalence ratio of mixed gas on explosion fireball radius (continued)
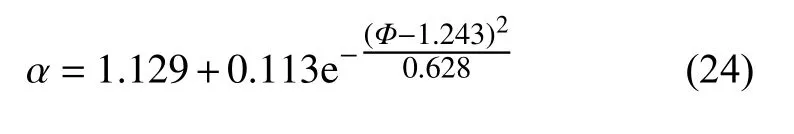
因此,考虑氢气-甲烷-空气混合气体当量比影响的爆炸火球半径可通过下式计算

3.3 可燃云团尺寸对混合气体爆炸传播的影响
本小节采用的氢气/甲烷/空气混合体系的氢气摩尔分数为75%,可燃混合物当量比为1.通过改变可燃云团尺寸(1 m3,4 m3,8 m3),研究氢气/甲烷/空气混合气体爆炸的尺寸效应.
图11 为三种尺寸混合气体爆炸时的最大爆炸超压,图中的实心符号为实验数据.可以看出当可燃云团尺寸增大时,由于内部可燃气体量增加,化学反应生成热积累量增加,使得各位置处的最大爆炸超压均增大.图11 中虚线为利用3.1 小节中建立的考虑混合物氢摩尔分数的TNT 当量理论模型计算得出的不同位置处的最大爆炸超压.可以发现,理论模型无法应用于不同体积的混合云团爆炸.而经典的TNT 当量法计算固体、液体类易燃易爆危险化学品时,其可以忽略体积效应带来的影响,具有较高的精度,但对于易燃易爆气体,其密度较低,忽视此体积效应时,理论模型误差较大.通过分析可以发现,TNT 当量法计算过程中,与可燃气体体积相关的参数可能为mTNT,因此将其与可燃云团进行关联发现混合气体爆炸满足以下关系时,理论模型计算结果(图11 中实线所示) 与实验数据吻合较好.在利用TNT 当量法计算气体最大爆炸超压时,必须考虑气体尺寸带来的影响
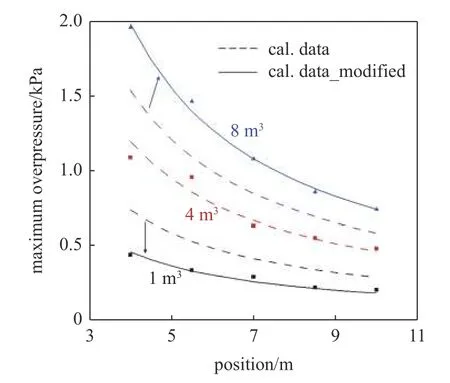
图11 混合气体尺寸对最大爆炸超压的影响Fig.11 Effect of mixtures size on maximum explosion pressure

本研究中选取的三种尺寸的可燃云团尺寸远小于实际事故中可燃云团的体积,根据建立的爆炸效率理论模型可知,实验中的爆炸效率远小于事故统计得出的爆炸效率数据.这与3.1.1 小节中的猜想一致.
图12 为不同可燃气云尺寸条件下爆炸火球半径随时间的变化规律.当可燃云团体积为1 m3时,31.5 ms 时,火球平均半径约为0.5 m,此时,火球半径等于可燃云团边长的1/2.可燃云团体积为4 m3时,在33.6 ms 时火球平均半径约为0.5 m,在50.4 ms 时火球平均半径约为可燃云团边长的1/2,即约为0.8 m.可燃云团体积为8 m3时,在40 ms 时火球半径约为0.5 m,64.0 ms 时火球平均半径约为0.8 m,78.4 ms 时火球平均半径为可燃云团边长的1/2,即1 m.随着可燃云团初始体积的增大,火焰到达某一位置处的用时逐渐增加,但增幅较小.可燃云团初始体积为1 m3,4 m3,8 m3时,火焰自加速指数分别为1.23,1.22,1.18,火焰自加速指数随着初始可燃云团体积的增大逐渐减小.
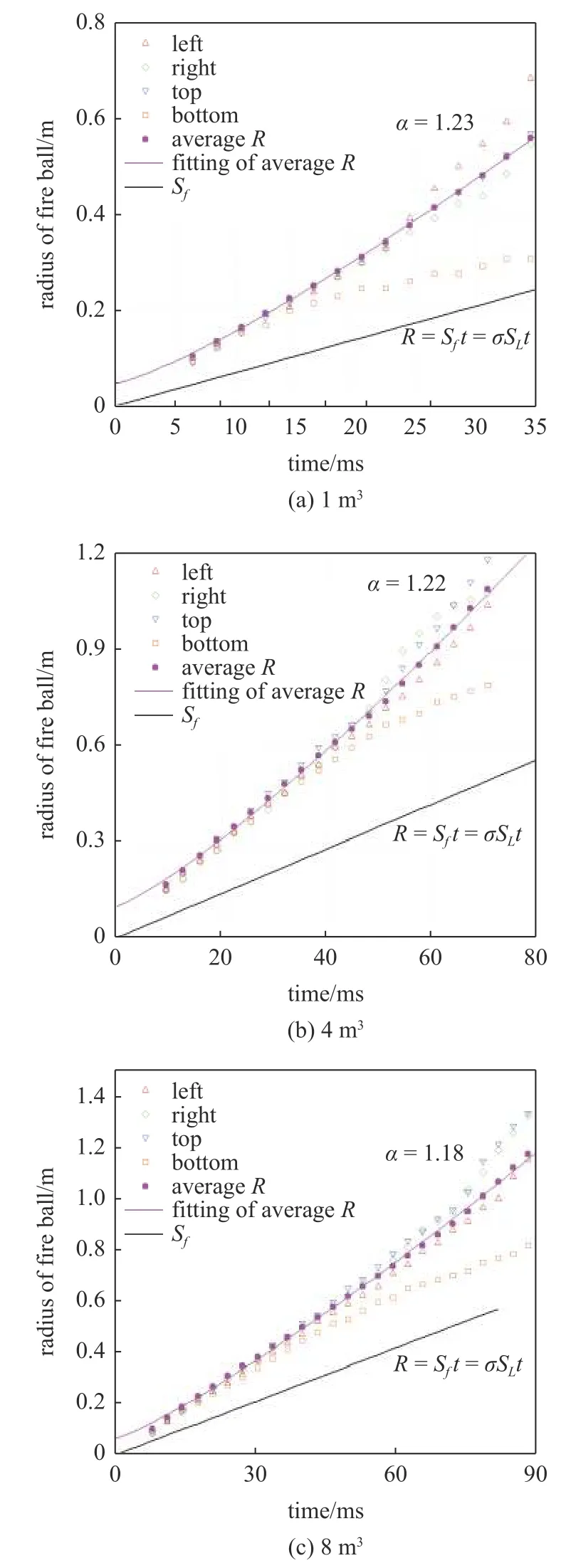
图12 可燃气云尺寸对爆炸火球半径的影响Fig.12 Size effect of mixed gas explosion on fireball radius
3.4 障碍物约束对混合气体爆炸传播的影响
图13 为障碍物约束对爆炸压力的影响.图中P1~P5 分别为4 m,5.5 m,7 m,8.5 m,10 m 位置处的爆炸压力曲线.4 m 位置处,无约束、仅背板约束、背板约束和顶板约束同时存在三种工况的最大爆炸超压约为1.092 kPa,1.252 kPa,1.386 kPa,后两种工况的最大爆炸超压为无约束条件下最大爆炸超压的1.15 和1.27 倍.
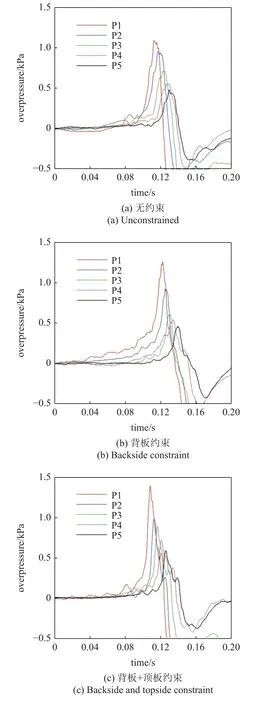
图13 障碍物约束对爆炸压力的影响Fig.13 Effect of constraint on explosion pressure
图14 为不同约束条件下侧方与前方爆炸超压曲线.P1~P5 的压力测点位于混合气体云团的右侧,P1′~P5′的压力测点位于混合气体云团的前方.前方各测点与点火位置的水平距离与右侧测点相同.4 m 位置处背板约束、背板约束和顶板约束同时存在两种工况混合气体云团前方的最大爆炸超压约为1.239 kPa 和1.494 kPa,分别为无约束条件下4 m 位置处最大爆炸超压的1.03 和1.37 倍.因此可以看出,障碍物约束可以增强其他几个无约束方向的爆炸超压.背板约束能够增强可燃气体云团侧方爆炸超压,但对前方的爆炸超压的影响较小.当背板约束和顶板约束同时存在时,对侧方和前方的爆炸超压具有明显的增强.Cai 等[38]研究表明,当系统内物质体系及反应物的量确定时,最大爆炸超压与物质体系的湍流强度呈线性增加.当仅存在背板约束时,背板边缘附近会使得侧方向的湍流强度增加,增大了侧方的爆炸压力.而背板约束与顶板约束同时存在时,背板的存在同样增强了侧方爆炸压力.同时,由于顶板的存在,可燃气团前方的气体湍流强度增加,增大了可燃云团前方的爆炸压力.另一方面,当仅存在背板时,压力到达背板后,会产生反射压力,使得前方压力略微增大.而背板与顶板同时存在时,背板、顶板及地面的反射压力会使得前方及侧方的爆炸压力增大.
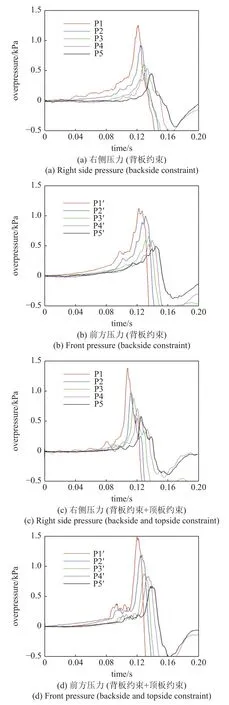
图14 不同约束条件下侧方与前方爆炸超压曲线Fig.14 Explosion overpressure curve at the side and front point under different constraints
图15 为壁面约束对爆炸火球扩展过程的影响.从图中可以看出,三种工况火焰面的褶皱程度基本一致,没有明显的区别.火球发展前期,三种工况下火焰发展趋势基本一致,无明显区别.火球发展到后期时,无约束和背板约束两种情况火焰发展趋势相差不大.而背板加顶板两种约束同时存在时,可以看出,上下两个方向的火焰发展较慢,左右两个无约束方向上的火焰发展速度较快.值得注意的是,由于顶板面积远小于地面面积,因此,爆炸压力能够通过顶板两侧泄放,这导致顶部火焰发展与地面相比略快,且火焰宽度比地面方向火焰宽度略宽.
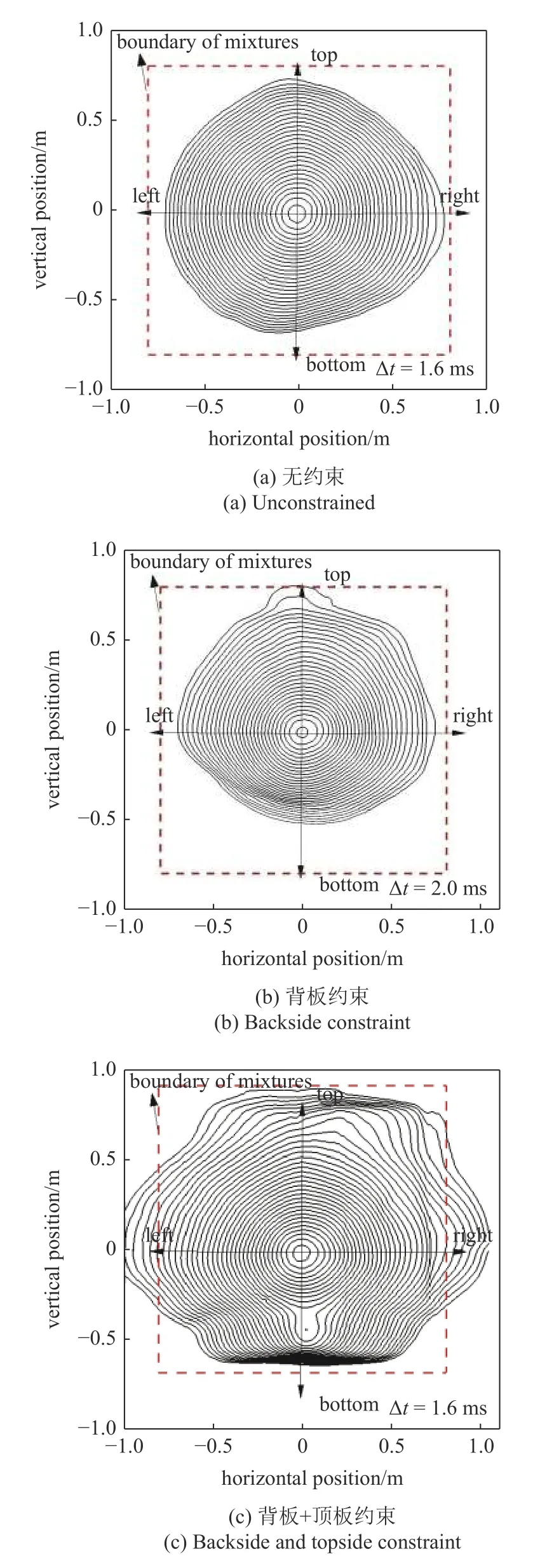
图15 壁面约束对爆炸火球扩展过程的影响Fig.15 Effect of constraint on explosion fireball expansion process
为了更好地研究壁面约束作用,对比分析了正视图和侧视图两个方向的火焰发展情况,如图16 所示.可以看出,仅有背板约束时,由于地面和背板的约束,两个方向的火焰传播受到明显阻碍,背板后方由于火焰的翻卷,仍然可以观测到火焰.但背板方向火焰传播与其他几个方向传播速度明显较慢,其他几个无约束多方向的火焰传播基本一致.当背板约束和顶板约束同时存在时,左、右、前方三个方向的火焰传播基本一致.同样地,上方虽然有顶板存在,但火焰仍会翻卷至顶板上方.对比两种不同约束条件下爆炸火焰传播情况,可以看出,由于顶板的存在,加速了左、右、前三个方向火焰的传播.

图16 不同约束条件下对各个方向火焰发展的影响Fig.16 Influence of different constraints on flame development
图17 为不同障碍物约束条件下爆炸火球半径随时间的变化规律.无约束时,上、下、左三个方向火焰传播规律基本一致,底边火焰传播与其他几个方向开始时基本一致,随后火焰逐渐趋向极限半径(0.8 m).仅有背板约束时,上、下、左、前四个无约束方向的火焰传播规律相差不大,底边火焰发展随着时间的推移逐渐变缓.当背板约束和顶板约束同时存在时,无约束的左、右、前三个方向的火焰传播规律基本相同,由于地面的存在,底边火焰发展有一个上限值.上方火焰开始发展时与左、右、前三个方向的传播相差不大,后期火焰传播逐渐变慢,但与底边方向不同的是,由于顶板面积有限,因此火焰发生翻卷后,仍会继续传播,顶板仅在一定程度上减缓了火焰传播速度.对比三种不同约束条件下的火焰发展,50 ms 时,无约束条件下左、右、上、下四个方向的火球半径分别为0.706 m,0.782 m,0.734 m,0.653 m;背板约束条件下左、右、上、前四个方向的火焰半径分别为0.745 m,0.838 m,0.879 m,0.814 m;背板约束和顶板约束同时存在的条件下,左、右、上、下、前五个方向的半径分别为0.868 m,0.929 m,0.830 m,0.611 m,0.943 m.可以看出,障碍物的出现会使得无约束方向的爆炸火焰传播速度增加,背板和顶板约束同时存在时火焰传播最快.
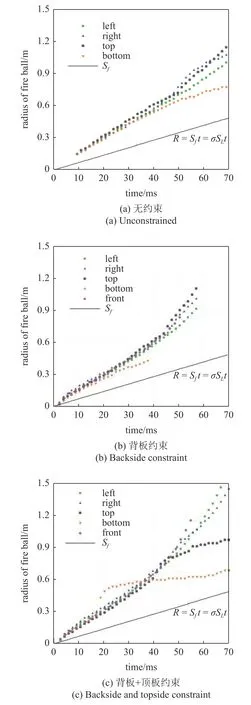
图17 障碍物约束对爆炸火球半径的影响Fig.17 Influence of obstacle constraint on explosion fireball radius
3.5 大尺度混合气体爆炸数值时空演化模拟研究
采用当量比为1、氢摩尔分数为75%和66.67%的氢气/甲烷/空气混合物,进行了数值模拟.可燃云团体积为4 m3.图18 为1 号传感器位置处(P1)最大爆炸超压的数值模拟与实验数据的对比图.可以看出,数值模拟结果与实验数据吻合较好.爆炸压力上升及下降趋势基本一致.由于实验受外界风速、聚乙烯薄膜等条件的影响,压力曲线出现小幅波动.且最大爆炸超压略大于数值模拟结果.
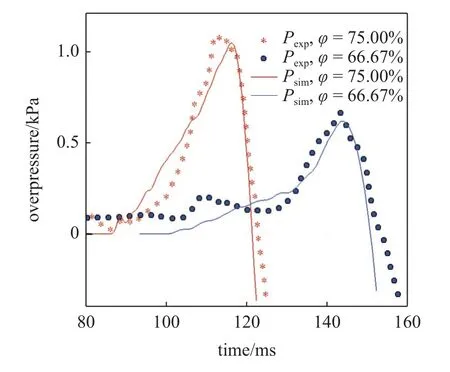
图18 实验与数值模拟结果对比(P1)Fig.18 Comparison of experimental and numerical simulation results (P1)
以实际加气站为参考,模拟了背板约束(#1)、顶板约束(#2)、背板和顶板同时存在(#3)三种工况(图19).可燃混合气体当量比为1、氢摩尔分数为75%,可燃云团体积为42.875 m3.点火区域位于四个加气机中心高1 m 位置处.计算区域为16.8 m ×16.8 m × 8.4 m,房屋及顶棚高度为3.5 m.压力测试点分别位于前方和侧方,距点火点中心6 m 位置处.
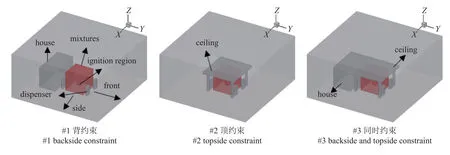
图19 数值模拟模型Fig.19 Model of numerical simulation
图20 为三种不同建筑结构条件下典型时刻的火焰面,图21 为不同方向的爆炸火焰锋面位置(火焰面温度取值为T=1500 K).22 ms 时,火焰刚开始发展,三种加气站内混合气体爆炸火球形状均以球形火焰为主,此时火焰处于加速发展时期.38 ms 时,加气站前方火焰速度达到最大值,火焰达到加气机附近.54 ms 时,火焰处于减速发展阶段此时#1 加气站与#2 和#3 加气站内混合气体爆炸火焰形状存在明显不同.#1 加气站对爆炸火球的影响较小,火焰呈半球形发展,而#2 和#3 加气站内,气体爆炸火焰在水平方向的扩展逐渐减缓,但由于顶棚的作用,开始出现翻卷火焰.三种建筑结构爆炸范围逐步开始出现差别,#3 加气站建筑结构内气体爆炸火焰传播范围较其他两种工况略大.84 ms 时,爆炸火焰传播速度相对稳定,且发展速度较为缓慢,#1,#2,#3 三种加气站内爆炸火焰稳定速度分别约为12 m/s,19 m/s,25 m/s.部分区域火焰开始出现火焰回退现象.120 ms 时,爆炸火焰虽然在持续外延传播,但回退区域逐渐扩大,尤其是在顶棚边缘处翻卷的火焰回退现象尤为明显.
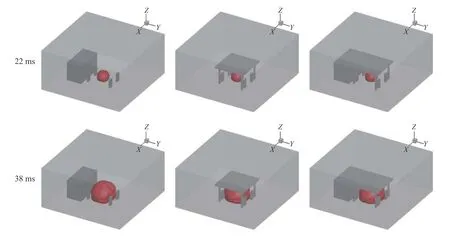
图20 不同时刻的火焰面(T=1500 K)Fig.20 Flame surface at different times (T=1500 K)

图20 不同时刻的火焰面(T=1500 K) (续)Fig.20 Flame surface at different times (T=1500 K) (continued)
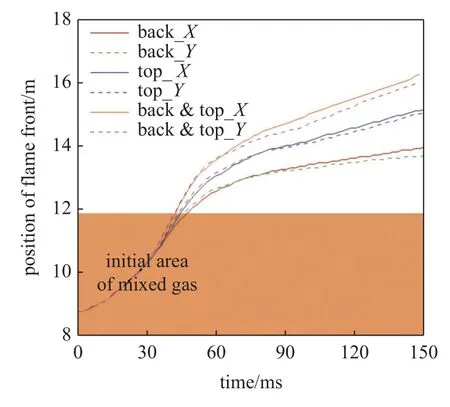
图21 不同方向的爆炸火焰锋面位置(T=1500 K)Fig.21 Position of explosion flame front in different directions (T=1500 K)
以点火中心为基点,给出了不同时刻XOY,XOZ,YOZ三个切面的火焰发展切面图,如图22 所示,时间均为0~ 152 ms,相邻等值面时间间隔为2 ms.三个方向开始阶段的发展基本一致,建筑结构的约束作用很小.火焰发展后期,#1 加气站爆炸火焰等值面密集,这说明后期火焰发展速度最慢,#3 加气站内爆炸火焰发展速度最快.通过切面可以明显发现#1 加气站内爆炸火焰回退现象较小,仅有建筑结构附近的翻卷火焰有回退现象.#2 和#3 两加气站内,除翻卷火焰有无火焰区域外,XOY水平切面也可以观测到大面积无火焰区域,#3 加气站尤为明显.

图22 火焰面演化情况(T=1500 K,t=0~152 ms,Δt=2 ms)Fig.22 Evolution of flame surface (T=1500 K,t=0~152 ms,Δt=2 ms)
为了进一步研究火焰时空演化规律,图23(a)和图23(b)给出了120 ms 时三种加气站XOY平面内氢质量分数、温度与流线分布图.可以看出,此时氢质量分数整体偏小,并且质量分数较大的区域大部分分布在火焰面附近.火焰内部区域的燃料基本被完全消耗.但通过温度与氢质量分数云图对比可以看出,氢气的消耗并不是火焰回退的原因.通过对平面内各关键位置处流线分析可以发现,在翻卷火焰位置处,出现了明显的涡,涡的存在一方面使得火焰发生翻卷,另一方面靠近建筑物处的空气大量涌入火焰内部,使得火焰面回退.为了确定这一现象,给出了120 ms 时XOY,XOZ,YOZ三个方向的切面云图,如图23(c)所示.可以看出,涡流现象是导致火焰回退的根本原因,火焰内部新鲜空气几乎到达地面处.由于涡的存在,建筑物附近的气体湍流强度明显增加,这进一步给出了3.4 小节中障碍物对侧方及前方爆炸压力的影响机制.
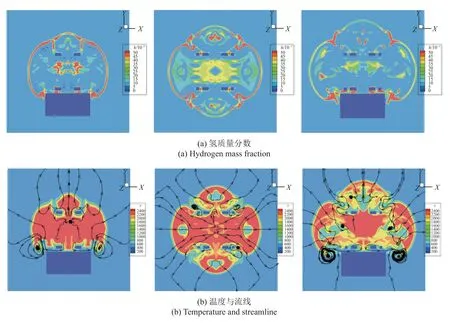
图23 三种加气站特征参数云图(t=120 ms)Fig.23 Contour of characteristic parameters of three gas stations (t=120 ms)
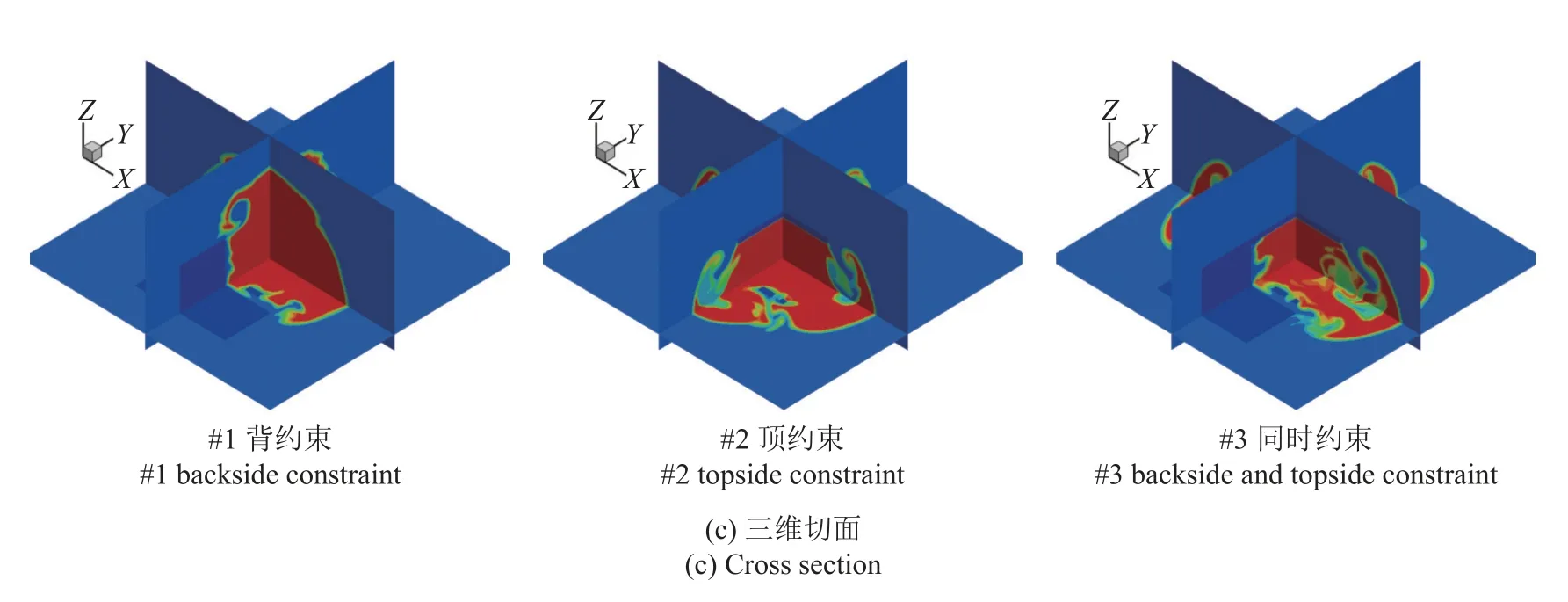
图23 三种加气站特征参数云图(t=120 ms) (续)Fig.23 Contour of characteristic parameters of three gas stations (t=120 ms) (continued)
图24 为三种加气站前方和侧方监测点压力变化曲线.#1 加气站内部混合气体爆炸时,正前方最大爆炸超压约为8.9 kPa,侧方最大爆炸超压约为9.57 kPa,侧方压力略大于前方压力.#2 加气站正前方的最大爆炸超压和侧方最大爆炸超压几乎一致,约为12.22 kPa,是#1 加气站的1.27~ 1.37 倍.#3 加气站正前方和侧方的最大爆炸超压约为17.35 kPa和17.67 kPa,较为接近.分别是#1 和#2 加气站的1.85~ 1.95,1.42~ 1.45 倍.与实验相比,数值模拟增大倍数更大,这主要是因为实验采用的钢板及钢骨架在爆炸后期会产生轻微移动,这吸收了部分爆炸能量,而数值模拟中的建构筑物均为刚性壁面,且未考虑壁面热损失,因此数值模拟数据大于实验数据.
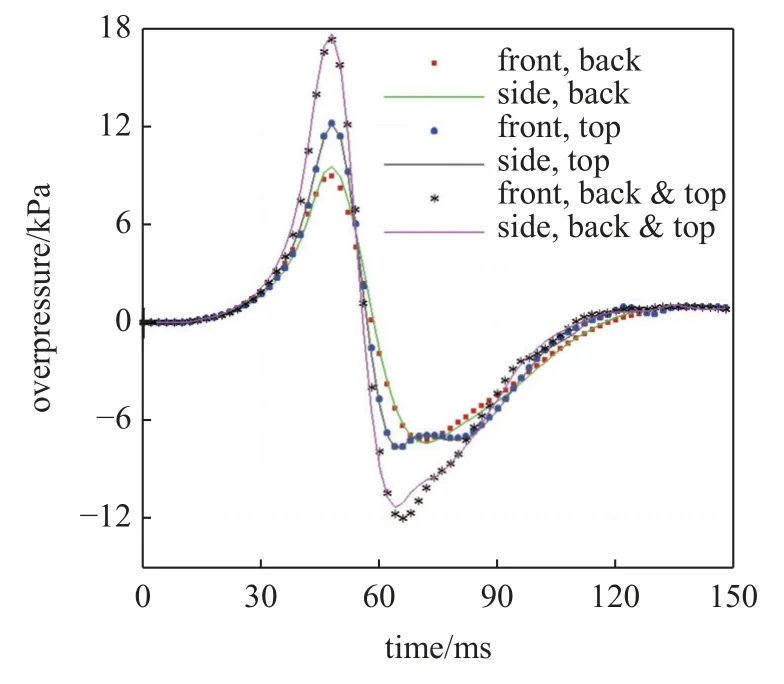
图24 不同方向的爆炸压力曲线Fig.24 Explosion pressure curve in different directions
4 结论
本文采用实验与数值模拟相结合的方法,研究了氢气-甲烷-空气混合气体在开放空间的爆炸时空演化规律,给出了氢摩尔分数、混合物当量比、混合气体云团尺寸、障碍物约束等对爆炸传播的影响,主要结论如下.
(1)最大爆炸超压随氢摩尔分数的增大而增大,可燃云团体积相同的条件下TNT 当量法预测爆炸超压时考虑氢摩尔分数影响的爆炸效率模型η=2.06002×10-12φ5.08952.氢摩尔分数越大,爆炸火焰自加速指数越大.建立了考虑不同氢摩尔分数的氢气-甲烷-空气爆炸时爆炸火球半径的预测模型为.各位置处 的最大爆炸超压随氢摩尔分数的增大而增大.
(2)氢气-甲烷-空气混合气体当量比从0.8 增加到1.4 时,混合气体爆炸的最大爆炸超压先增大,后减小,最大值发生在当量比为1.1 时.随着当量比的增加,火焰自加速指数先增大后减小,当量比为1.2 时,火焰自加速指数最大.建立了考虑混合气体当量比的爆炸火球半径的预测模型为R=R0+Atα=
(3) TNT 当量法无法准确预测不同云团尺寸条件下的最大爆炸超压.尺寸效应对可燃云团爆炸效率的影响满足火焰自加速指数随着初始可燃云团体积的增大逐渐减小.随着混合气体云团的增大,会使得压力传播变慢,但爆炸强度增强.
(4)障碍物约束可以增强其他几个无约束方向的爆炸超压.背板约束能够增强可燃气体云团侧方爆炸超压,但对前方的爆炸超压的影响较小.当背板约束和顶板约束同时存在时,对侧方和前方的爆炸超压具有明显的增强.仅有背板约束时,后方和地面两个方向的火焰传播受到明显阻碍,背板后方出现火焰翻卷现象,其他几个无约束多方向的火焰传播基本一致.背板约束和顶板约束同时存在时,左、右、前方三个方向的火焰传播基本一致.顶板处火焰发生翻卷.顶板的存在加速了左、右、前三个方向火焰的传播.
(5)加气站内不同建构筑物条件下爆炸火焰传播距离、传播速度、最大爆炸超压等关键参数明显不同.#3 加气站水平方向的毁伤范围及破坏程度最大,#2 加气站次之,#1 加气站最小.因此在划定加气站安全距离时,应充分考虑不同建筑结构的影响.

