空心瓷绝缘子机械特性的试验分析研究

井 谦， 胡文歧， 张长征， 刘志强， 何远华， 彭 静， 刘于新， 危 鹏

(西安高压电器研究院股份有限公司，西安710077)

0 引言

空心瓷绝缘子是高压电器的重要组成部分，广泛应用于各种电压等级变电设备，具有良好的物理化学稳定性、热稳定性、电气和机械性能[1-4]。常用于变压器、断路器、电容器、互感器、避雷器和电缆终端等电气设备，需要长期承受各种机械负载[5-6]。空心瓷绝缘子组装在电气设备后有可能承受的弯曲应力包括端部机械负荷、内压力、短路负荷、覆冰负荷、操作负荷、风负荷、地震负荷等[7]，在这些因素的综合影响下，空心瓷绝缘子受力情况复杂。从理论上来说，随着制造技术的进步，目前主流水平的瓷件大多是由高强度瓷质构成，其稳定性和致密性很高，烧成工艺采用计算机程序控制，空心瓷绝缘子的抽样试验结果往往优于技术设计参数，空心瓷绝缘子出现安全事故的概率应该是比较小的，但实际中却时有发生意外。

近年来，多地发生空心瓷绝缘子在安装或运行过程中断裂或爆炸，由此引起的各种电网事故严重影响电网的安全稳定性和可靠性，特别是当空心瓷绝缘子发生粉碎性爆炸引发的二次事故问题更是有可能造成重大的安全事故。影响断裂的因素较多，大部分情况下对断裂的原因溯源分析并不容易，尤其是粉碎性爆炸常常难以直接找到关键的佐证。虽然抽样试验的破坏强度会高于额定弯曲强度，但由于生产工艺的波动导致产品的破坏值存在一定的波动性和分散性。

基于上述背景，利用动态电阻应变仪，参照标准GB/T23752-2009，研究分析空心瓷绝缘子分别在弯曲负荷、内压力负荷及两者联合作用下应力和应变变化规律。

1 动态应变测试方法

1.1 试验设备

动态电阻应变仪：设备型号为DH8302，量程±100 000 με，电压示值误差为0.05%F.S，温漂小于0.05 με/℃，时漂小于1 με/天，16通道。采用1/4桥测量，设置采样频率为1 000 Hz，应变片电阻120.1±0.1 Ω，灵敏系数K=2.14±1%。

大型弯扭试验机型号为WNW-200，最大弯矩700 kN·m，最大扭矩40 kN·m，准确度等级为1.0级。

电动试验泵型号2D-SY 71/40，数字精密压力表型号CYF-100，准确度等级为0.25级。

1.2 测量系统原理

电阻应变仪设备测量的原理是将粘贴在被测试件上的电阻应变片的电阻变化率△R/R转换成电压变化输出，再经放大电路放大，然后经电信号采集系统收集，利用成套软件可以实时显示波形，并可以进行相关数据处理。

由于机械应变一般都很小，要把微小应变引起的微小电阻变化测量出来，同时要把电阻相对变化ΔR/R转换为电压的变化，因此需要有专用测量电路用于测量应变变化而引起电阻变化的测量电路，通常采用惠斯通电桥，其有四个桥臂R1、R2、R3、R4按顺序接在A、B、C、D之间，如图1所示。

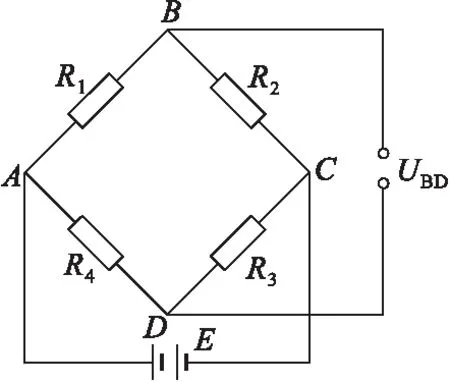
图1 惠斯通电桥示意图Fig.1 Schematic diagram of Wheastone bridge

电桥的对角点AC接电源E，另一对角BD为电桥的输出端，其输出电压UBD经计算输出电压为[8]

(1)

可知当R1×R2=R3×R4时，UBD=0，这是电桥平衡的条件。

在实际测试中，随着被测试件的变形，四个桥臂上的电阻应变片都会发生微小变量，各电阻应变片的电阻变化为ΔR1、ΔR2、ΔR3、ΔR4，各电阻应变片所感受的应变量分别为ε1、ε2、ε3、ε4，通过理论推导计算，可以得出UBD的变化量：

(2)

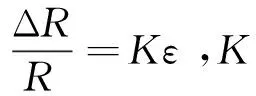
当电桥中只有一个桥臂参与机械变形时，由公式(2)可以得知ε1=4ΔUBD/EK，即电阻应变片的应变量正比于输出电压ΔUBD，通过测量电压信号即可计算出被测试件的应变量。

1.3 试验样品及测量方法

本研究选用的空心瓷绝缘子绝缘子样品高度1 830 mm，瓷件内径Di为175 mm，外径D0为245 mm，端部附件密封直径Ds为210 mm，额定弯曲破坏负荷为22 kN，额定内水压负荷为4.5 MPa。在样品上端和下端处共布置4只轴向应变，分别为应变1、应变3、应变5和应变7；4只径向应变片，分别为应变2、应变4、应变6和应变8。其布置及其粘贴位置示意图如图2所示，上下应变片均离端部附件约40 mm。应变的正负号分别代表拉应力和压应力。相邻轴向应变和径向应变的粘贴距离为5 mm，因距离较小，可近似认为两者等同于同一微小区域的应变。试验时对样品进行了3次重复性试验验证，以防止单次试验的随机性结果。

图2 应变片粘贴位置示意图Fig.2 Schematic diagram of strain gauges with sticking position

为考察空心瓷绝缘子的弯曲试验、内压力试验及两者联合试验作用下的机械特性，并参考GB/T23752-2009中对试验的规定，特设计加载过程如下：

1)弯曲试验：以0.2 kN/s的加载速率连续施加弯曲试验负荷，且每增加2 kN，即2 kN、4 kN、6 kN…22 kN负荷下均保持30 s，弯曲负荷连续不间断；

2)内压力试验：以2 MPa/min的加载速率连续施加内压力负荷，且每增加0.5 MPa，即0.5 MPa、1.0 MPa、1.5 MPa…4.5 MPa负荷下均保持30 s，内压力连续不间断；

3)弯曲及内压力联合试验：为模拟空心瓷绝缘子的真实运行状况，先将内压力以2 MPa/min的加载速率加压至4.5 MPa下，保持内压力不变，再以0.2 kN/s的加载速率连续施加弯曲试验负荷，且每增加2 kN，即2 kN、4 kN、6 kN…22 kN负荷下均保持30 s，弯曲和内压力负荷连续不间断。

2 实验结果与分析

2.1 不同弯曲负荷状况下的应变分析

图3为不同弯曲负荷状况下空心瓷绝缘子应变曲线。从图3(b)中可以看出，轴向状态下，随着弯曲负荷的不断增加，四个轴向应变值都不断增大，且基本呈等比例增加。由于弯曲负荷施力点位于样品的顶端，样品下端的轴向应变1和应变3增加明显，上端处的轴向应变5和应变7虽略又增加，但增幅不明显。

从图3(c)中可以看出，径向状态方面，因样品主要受由弯矩引起的轴向变化作用，四个径向应变随弯曲负荷的增加，变化较轴向小。在上端处，应变8基本无变化，表明这区域处径向不是受力的主要方向，而应变6却在弯曲负荷2 kN后呈略微减小趋势。此外，下端径向受力状态与轴向相反，如轴向应变1是拉应力状态，相应的径向应变2为压应力状态，应变3是压应力状态和应变4为拉应力状态。

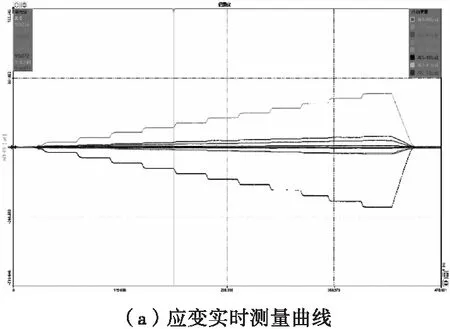
图3 不同弯曲负荷状况下空心瓷绝缘子应变曲线Fig.3 The strain curves of the hollow ceramic insulator under different bending loads

将轴向应变1、应变3、应变5和应变7的曲线进行回归直线方程分析，拟合后的直线如公式(3)～(6)所示：

y1=14.667x-5.06500

(3)

y3=-12.358x-2.755

(4)

y5=1.779x+1.401000

(5)

y7=1.588x-0.491000

(6)

相应应变的拟合优度因子R2分别为

在统计学中通常使用拟合优度因子R2评估回归直线对实测值的拟合程度[9]，取值范围是[0,1]，R2的值越接近1，说明回归直线对实测值的拟合程度越好；反之，R2的值越接近0，说明回归直线对观测值的拟合程度越差。实际拟合后的R2的值非常接近1，说明这4个轴向应变的直线度很高，对于脆性材料处在弹性变形阶段，适合后续弹性模量的计算。

在拟合的线性公式中，从直线斜率的绝对值可以看出拉应力状态的斜率要稍微大于压应力状态下的斜率，表明陶瓷材料的拉伸弹性模量和压缩弹性模量不同。

2.2 不同内压力负荷状况下的应变分析

图4为不同弯曲负荷状况下空心瓷绝缘子应变曲线。从图4(b)中可以看出，轴向状态下，随着内压力值的不断增加，轴向应变不断增大，与弯曲负荷下类似，基本也成等比例增加，且上端和下端的轴向应变变化偏差较小，变化一致性较好，表明由内压力引起的轴向拉伸变化量差异很小。从图4(c)中可以看出，径向方向下的变化规律与轴向方向类似，但不同的是，相同内压力状态下，径向的应变要稍微大于轴向的应变，说明在内压力试验下，空心瓷绝缘子径向受到的应力要大于轴向，样品受到的“膨胀”作用大于“拉伸”。

图4 不同内压力负荷状况下的应变曲线Fig.4 The strain curves of the hollow ceramic insulator under different internal pressure

从现有的测量数据分析，样品的径向变化呈现出沿轴向方向的同侧面一致性，即应变2与应变6、应变4与应变8高度一致。由于伞间距太小，样品的中部没有粘贴应变片，所以从现有数据还不能判断径向同侧一致性是个例，还是普遍现象，还有待进一步积累更多的试验数据，或研究开展一些数据模拟验证工作。

值得一提的是，从应变实时测量曲线可以看出，在初始状态升压过程中时，应变的测量值突变较大，或者是在压力值瞬间增大时，瞬间应变突变较大，这些过程不是连续平稳状态，待压力值稳定后，恢复常态。这与弯曲负荷状态下的平滑应变实时测量曲线截然不同，原因可能是与这两种不同的加载方式有关，弯曲负荷加载是设定好的一整套完整自动加载程序，伺服电机控制的弯曲力是稳定持续上升，而由于电动水压泵加压的工作原理主要是往复式柱塞泵的循环动作将水介质高压挤入样品内，这个过程有一定的波动性和类似的脉冲性，平稳性一般，导致了内压力改变的时候应变值有突变现象，也有可能是水介质在挤入样品内腔时，水溶液压缩过程中引起的固有频率变化，造成瞬间共振，后续还有待进一步试验分析研究。所以在某些特殊情况下(如断路器)，尤其要考虑到开断操作后的瞬间压力升高变化率，这有可能是考验空心瓷绝缘子质量可靠性的关键。

2.3 弯曲及内压力联合试验状况下的应变分析

图5为不同弯曲负荷状况下空心瓷绝缘子应变曲线。从图5(b)中可以看出，轴向应力状态下，联合试验状况下的应变变化规律与弯曲负荷试验下高度一致，但不同的是，因为先将内压力加压至4.5 MPa下，保持内压力不变，再依次加载负荷，所以弯曲负荷为零时，轴向应变已有变化，增加幅度基本相同，数值为正，此时样品全部为拉应力状态。此后随着弯曲负荷的增加，与单纯弯曲负荷下的轴向曲线相比，联合试验状况下的曲线将整体上移，这就意味着呈拉应力状态的应变1和应变5将会变得更大，而呈压应力状态的应变3和应变7将会变小。

从图5(c)中可以看出，径向应力状态方面，因内压力的存在，径向应变已有变化，与单纯弯曲负荷下的径向变化曲线相比，最大的不同的是，应变2符号为正，表明原来单纯弯曲下表现出的径向压应力，由于内压力的存在，此处位置的径向方向的应力发生了改变，即呈拉压力。但此时变化存在不一致性，2.2小节已进行说明。

图5 弯曲及内压力联合试验状况下的应变曲线Fig.5 The strain curves of the hollow ceramic insulator under the combination of bending load and internal pressure

以应变1和应变2所处的局部区域为例，轴向应变1的拉应力因内压力的存在变得更大，而径向应变2由原来的压应力改变为拉应力，应力状态发生改变，此时微小区域的平面应力图，如图6所示。

陶瓷材料塑性变形能力极差，其断裂是以各种缺陷为裂纹源，裂纹尖端易引起很高的应力集中，在一定的拉伸应力下，其最薄弱环节处的微小裂纹扩展，当裂纹达到临界尺寸时容易失稳，不经过塑性阶段，会瞬间发生断裂。而在压缩应力时，裂纹闭合或呈稳态缓慢扩展，压缩强度较高。所以在单纯的弯曲负荷下，轴向为拉应力，径向为压应力，若此时最薄弱裂纹的方向恰巧受压应力作用，则样品的弯曲强度可继续表现出较高的状态。而当在弯曲负荷和内压力联合作用下，微单元轴向和径向全部受拉应力作用，无论裂纹方向如何分布，此微小区域所经受的考核将会变得更加严酷。空心瓷绝缘子在实际运行过程中，往往也是同时受到一定的弯曲负荷和内压力联合作用，某些特殊原因下，受力情况更是复杂，所以在空心瓷绝缘子选型和技术参数设计等方面应充分考虑其使用环境和运行状况。

2.4 拉伸弹性模量和压缩弹性模量的计算

弹性模量是工程材料中一种重要、最具特征的力学参数，从宏观角度分析，弹性模量是衡量物体抵抗弹性变形能力大小的尺度，从微观角度来说，则是原子、离子或分子之间键合强度的反映，凡是影响键合强度的因素均能影响材料的弹性模量，如键合方式、晶体结构、化学成分、微观组织、温度等。弹性模量用E表示，定义为理想材料有弹性形变时应力(σ)与相应应变(ε)之比，单位为N/m2，如公式(7)所示。弹性模量是材料的本身属性，与外力大小及物体的形状无关。

(7)

弯曲负荷试验时，在忽略空心瓷绝缘子伞结构及上下端部金属附件对力学分析的影响下，可将空心瓷绝缘子简化成一个圆环柱体模型，根据材料力学计算公式[10]，圆环柱体截面上距离中性层为x的某一点的应力为

(8)

内压力试验时，按照GB/T 23752-2009附录D，如果假定内压力p导致的轴向应力是均匀的，轴向应力可以使用公式(9)简化计算：

(9)

式(9)中p是内压力，Ds是端部附件密封的直径，Ds=210 mm；Do是绝缘件主体外径，Do=245 mm；Di是绝缘件主体内径，Di=175 mm。

计算弹性模量的思路为：弯曲负荷试验时，以弯曲负荷增加间隔2 kN、4 kN、6 kN…20 kN计算基准，用“间隔力”以方便描述，然后计算相应间隔力下的应变增加值；同理，内压力试验下，以内压力增加间隔0.5 MPa、1.0 MPa、1.5 MPa…4.0 MPa为计算基准，再计算出相应间隔内压力下的应变增加值，得出各自间隔力下的拉伸和压缩弹性模量值。

根据应变的粘贴位置及测量值分析，因为上端部附件处受弯矩很小，应变值低，再加上应变的零点漂移因素等影响，误差容易放大化，不太适合弹性模量计算，所以采用下端附件处的轴向应变计算拉伸和压缩弹性模量。内压力试验时候，四个轴向应变的变化规律一致性较好，因此以内压力值计算拉伸弹性模量时，将该四处的拉伸弹性模量全部一起统计进行分析。

图7为弯曲及内压力试验下的拉伸和压缩弹性模量散点图，图中的连续曲线是由各自间隔力下计算的弹性模量平均值。从图中可以看出，无论是弯曲负荷试验还是内压力试验，间隔力或间隔内压力较小时，以此计算出的弹性模量波动较大，统计出的标准偏差较高，随着间隔压力或内压力的增加，弹性模量值逐渐趋于集中，波动范围收窄，标准偏差缩小。从3条平均值曲线分析，3条曲线几乎呈平直状态，前后相差不大，表明虽然当间隔力或内压力较小时，弹性模量波动较大，但其总体平均值与高负荷下计算的弹性模量平均值差别很小。

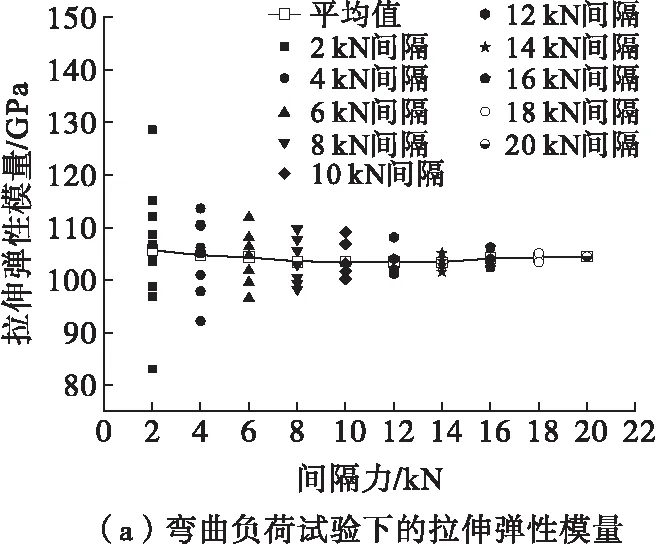
图7 弯曲及内压力试验下的拉伸和压缩弹性模量散点图Fig.7 The scatter diagram of the tensile and compressive elastic modulus under the combination of bending load and internal pressure

横向比较两种试验状况下的拉伸弹性模量，从统计数据上分析，图7(a)和(b)计算的拉伸弹性模量平均值范围分别为103.3 GPa～105.7 GPa和156.5 GPa～166.6 GPa，内压力试验下计算的拉伸弹性模量明显大于弯曲负荷试验下的值，原因也不难得出，对空心瓷绝缘子来讲，因内压力导致的轴向应变变化量最大还不到50微应变，远小于弯曲负荷引起的轴向应变，计算出的弹性模量误差易放大，从图7(b)也可以看出在低间隔内压力下计算的拉伸弹性模量波动范围远大于弯曲负荷试验下，最大至300 GPa，因此由内压力试验下计算的拉伸弹性模量可信度不高。

弯曲负荷试验下计算的压缩弹性模量范围为123.9 GPa～125.7 GPa，大于拉伸弹性模量。从理论上讲，弹性模量反映的是材料微观上原子支间结合力与平衡点间距的关系，依据胡克定律，原子间结合力在拉伸和压缩状态的应力与应变比值应是一个常数，拉伸弹性模量和压缩弹性模量应该是相同的。但对脆性陶瓷材料而言，弹性模量不仅与结合键有关，还与组成的种类、分布比例及气孔率有关，瓷件由晶相、玻璃相和气孔组成，由此易造成各种微缺陷和微裂纹[11]。受压缩应力时，裂纹闭合或呈稳态缓慢扩展，压缩强度较高，应变较小，导致压缩弹性模量较大。

从上述分析可得出，进行弹性模量测量时，在弹性变形阶段范围内，优先推荐选择以相对较大负荷为基准，这样不需要相对较多的重复测量计算，即可得到高准确性的试验结果。基于此，以最大弯曲负荷22 kN和内压力4.5 MPa为基准，结合泊松比的定义—径向应变εx与轴向向应变εy之比，可以得出拉应力和压应力状态下的计算的泊松比分别为0.14和0.17。

陶瓷材料由于脆性高，在拉伸负荷试验时易在夹持部位断裂，因此常用三点或四点弯曲加载方式进行抗弯负荷试验，以代替拉伸试验，测定其弹性弯曲挠度后，根据应力和应变可计算出弹性模量[12-14]。GB/T 10700-2006《精细陶瓷弹性模量试验方法 弯曲法》中规定了测试方法[15]，其中制备弯曲试样时对其相对面的平行度、相邻面的垂直度、表面粗糙度等要求较高，制备试样困难，因试样精细度非常高，试验过程中对试样具有一定的破坏性质，常不具有重复测试的机会，测试结果往往波动较大。综合比较分析，本研究中利用弯曲负荷试验下的拉伸和压缩弹性模量测量方式，是一种可重复测试、方便快捷和可靠性较高的测量方法，可应用于各种类型的空心瓷绝缘子弹性模量测量。

3 结论

本研究选用空心支柱瓷绝缘子作为试品，参照标准GB/T23752-2009，利用动态电阻应变仪，分别在弯曲负荷、内压力负荷及两者联合作用下，从微观上分析空心瓷绝缘子的机械特性和变化规律，得出了以下结论：

1)弯曲负荷试验下，随着弯曲负荷的增加，轴向应变不断增大，基本呈线性增加，下端径向受力状态与轴向相反，拉应力增长的速率稍大于压应力。

2)内压力试验下，内压力值瞬间改变增大时，瞬时应变突变较大。随着内压力的增大，轴向和径向应变不断增大，径向应变稍微大于轴向应变，上端和下端部位的轴向应变变化一致性较好。

3)弯曲负荷和内压力联合作用下，呈拉应力状态的应变大于单独负荷作用的应变，而呈压应力状态的应变则小于单独负荷作用的应变，下端拉应力测受力状态由轴向拉应力和径向压应力转变为轴向径向均为拉应力，考核将会变得更加严酷。

4)弹性变形范围内，推荐选择以相对较大弯曲负荷为基准，进行拉伸弹性模量、压缩弹性模量和泊松比的测量，是一种可重复测试、方便快捷和可靠性较高的测量方法，内压力试验不适合弹性模量的测量。