考虑零序不平衡电流的小电流接地系统故障选线研究

陈 涛, 李必伟, 韩 源, 李启林, 王建军, 井金全

(1.国网河南省电力公司漯河供电局，河南 漯河 462000；2.长沙理工大学电气与信息工程学院，长沙410114)

0 引言

配电网的电压等级一般为3～35 kV，具有供电面积广、容量大以及配电点多等特点[1]。为保证配电网供电的可靠性，我国中压配电网普遍采用不接地或消弧线圈接地。因此研究小电流接地系统故障选线就显得尤为重要。目前研究小电流系统大致可分为：通过检测故障时各线路零序电流的稳态选线法；检测故障时各线路能量变化的暂态选线法；通过切换中性点接地状态的主动式选线法等[2-4]。这些方法都是基于配电网处于平衡状态时的理论研究，并不能普遍适用于实际的运行的电网中。

配电网线路对地电容不对称、三相负荷不对称以及检测线路零序电流的互感器存在误差是不平衡电流存在的主要原因。文献[5]提出了一种针对于不平衡电流的改进导纳法来判断故障线路，利用该方法进行故障选线时可不考虑故障点过渡电阻大小的影响；文献[6]通过仿真分析研究了不平衡对故障选线的影响，得出在不平衡电网发生高阻接地时，暂态选线、稳态选线判据都存在误判的情况；文献[7]通过将不对称电网进行两次戴维南等效变换，研究了不平衡电流对小电流接地系统的影响；文献[8]通过导纳不对称的原理利用相关算法从而实现配电网不对称时的故障选线。

笔者通过建立相应数学模型，分析了配电网不平衡电流所产生的原因，并理论推导出小电流接地系统中的不平衡电流。通过研究系统故障前与故障后零序电流的变化，得出了考虑不平衡电流下小电流接地系统的选线新方法，并通过搭建相应的仿真模型验证该方法的有效性。

1 不对称电流分析

1.1 电流互感器不对称分析

配电系统中所使用的电流互感器制作工艺不同以及精度要求不够，使得所感应的零序电流在幅值和相位上不能真实的还原线路实际的零序电流，导致接地选线装置在实际中应用中频繁误选。若系统中采用误差较大、精度较低的电流互感器，可能会使二次侧输出的电流与实际电流相比，幅值误差有20%之多，相位角误差达5°以上。等值电路见图1。

图1 装设电流互感器的配电线路等值电路Fig.1 Equivalent circuit of distribution line equipped with current transformer

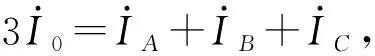
(1)

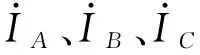
1.2 三相负载不对称分析

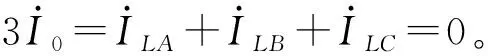
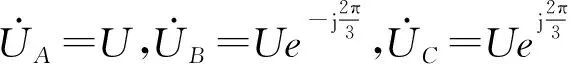
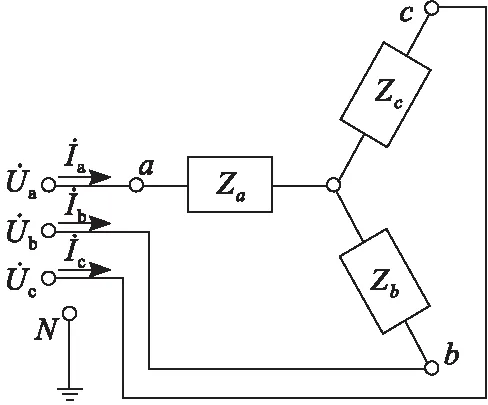
图2 三相星型负载Fig.2 Three-phase star load

图3 三相三角型负载Fig.3 Three-phase triangular load

根据KCL定律，可以得到以下公式：

(2)

把A相负荷电流看作平衡分量，式(2)可以改写为

(3)

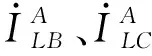
(4)

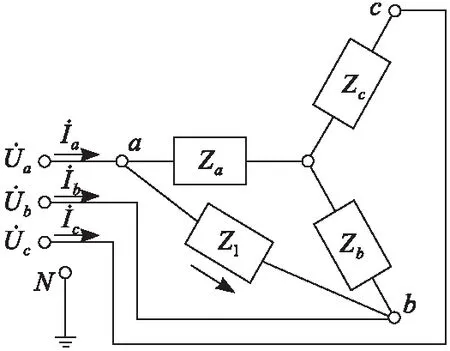
图4 等效原理图Fig.4 Equivalent schematic

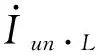
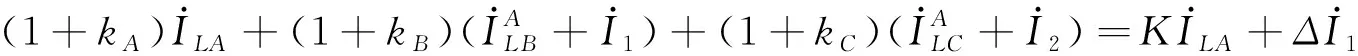
(5)

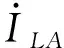
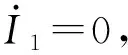
若系统发生单相接地故障时，故障点的过渡电阻并未改变负荷的拓扑结构，故障发生的较短时间内所接负荷几乎未发生波动。因此，故障后负荷零序电流不发生变化，故可以采用故障前后所测得的零序电流相减的方法消除负荷不平衡电流的影响。

1.3 对地电容不对称分析

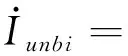
(6)

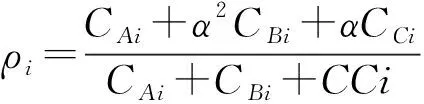
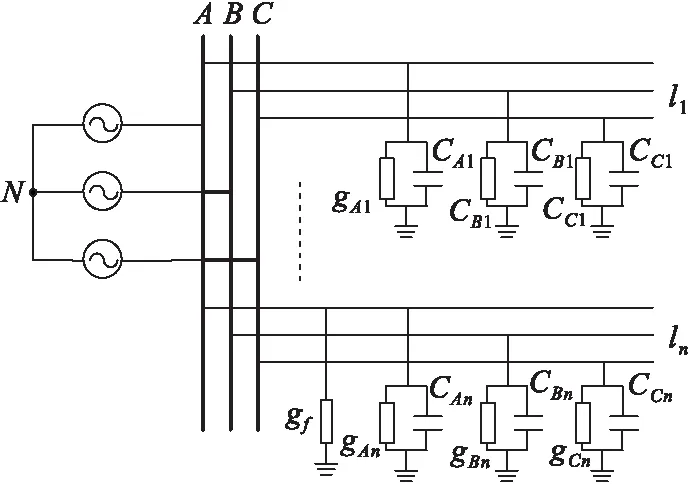
图5 不对称电网单相接地故障等值电路Fig.5 Equivalent circuit of single-phase grounding fault in asymmetric power grid

(7)

(8)

(9)

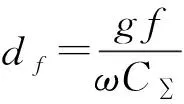
可得系统中非故障线路零序电流为

(10)

故障线路零序电流为

(11)

1)对地电容不平衡电流

故障馈线对地电容不平衡电流：

(12)

非故障馈线对地电容不平衡电流：

(13)

由式(13)(14)可以看出，各馈线对地电容不平衡电流大小方向取决于不对称电压和线路不对称因子，由于各馈线对地电容不对称因子的大小和方向存在随机性，故各馈线对地电容不平衡电流分布不存在规律性。对地电容不平衡电流分布如图6所示。

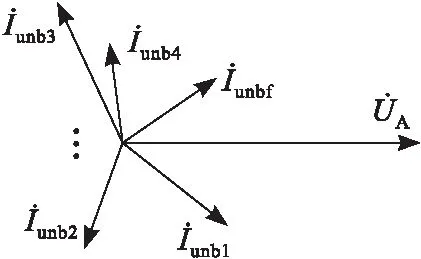
图6 对地电容不平衡电流分布图Fig.6 Unbalanced current distribution of the capacitance to ground

2)平衡电流：

故障馈线平衡电流：

(14)

非故障馈线平衡电流：

(15)

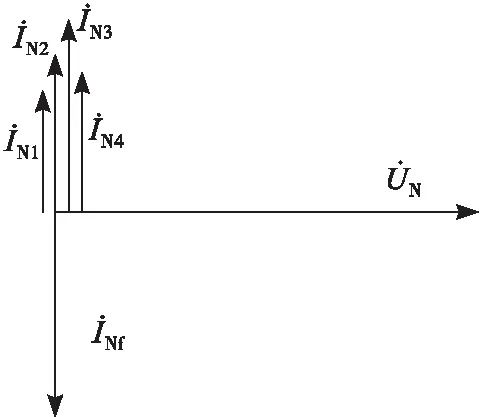
图7 中性点不接地系统平衡电流分布图Fig.7 Distribution diagram of the balance current of the neutral point ungrounded system

将故障前后各馈线零序电流做差可得，故障馈线零序电流：

(16)

非故障馈线零序电流：

(17)

对比分析可知，将故障前后各馈线零序电流做差后，故障馈线所得到的差值电流始终大于非故障馈线所得到的差值电流。

2 仿真验证

为验证理论分析所得结果，利用Matalab/simulink仿真平台搭建相应的模型。仿真中电源选择6 kV电源，通过变压器升压至10 kV，采用三相并联负载，系统整体有三条出线，线路的正、零序电阻为0.12、0.38 Ω/km，线路的正、零序电感为0.93、4.12 mH/km；为使线路中产生不平衡电流，设置馈线3为对称线路，其正、零序对地电容为0.08、0.13 μF/km，设置馈线1三相的对地电容分别为10.78、12.78、12.78 μF/km，馈线1的不对称度为5.52%，设置馈线2三相的对地电容分别为12.78、12.78、11.78 μF/km，馈线2的不对称对为2.69%。故障设置线路2的A相发生故障。得到表1、2。

表1 不同运行状态下各线路零序电流Table 1 Zero-sequence current of each line under different operating conditions

表2 各线路消除不平衡电流后的零序电流Table 2 Zero-sequence current after each line eliminates unbalanced current

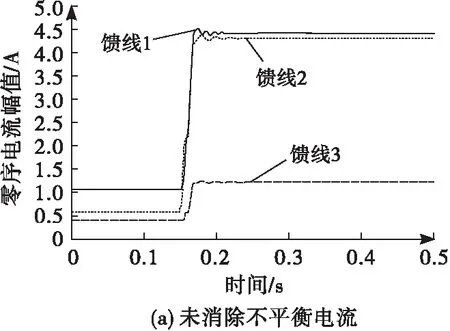
图8 过渡电阻为1 000 Ω时各馈线零序电流Fig.8 Zero sequence current of each feeder when the transition resistance is 1 000 Ω

根据表中数据可知在系统正常运行时，各线路中所存在的不平衡电流幅值与相位皆有较大区别；当线路2的A相发生单相金属性接地时，满足故障线路零序电流最大以及电流相位与非故障线路电流相位相反的检测要求；但随着过渡电阻的增大，故障线路零序电流幅值出现小于非故障馈线零序电流的情况，且故障线路与非故障线路的电流不满足相位相反的原则，相位甚至接近90°。因此在系统存在不平衡电流情况下，单纯利用比较零序电流大小以及故障线路与非故障线路相位相反的检测判据将会失效。经消除线路所产生的不平衡电流后，从表中可以看出故障线路与非故障线路的相位始终相反，且不随过渡电阻的变化而变化，故障线路的零序电流幅值始终保持最大，因此消除不平衡电流后，可以通过比较相位以及幅值大小可准确选出故障线路。

3 结论

笔者从配电网系统中的互感器不对称、三相负载不对称以及对地电容不对称三个方面分析了系统中不平衡电流产生的原因。建立相应的数学模型，理论分析了不平衡电流的主要原因在于对地电容不对称以及互感器不对称。并通过理论计算推导出系统各馈线故障前后包含不平衡电流的零序电流关系式，理论研究表明各馈线故障时零序电流减去故障前的零序电流，所得到的故障馈线零序电流始终大于非故障馈线零序电流，且故障馈线零序电流与非故障馈线零序电流相位相反。

为检验理论分析所得结论，利用Matalab/simulink仿真平台验证得出在系统存在不平衡电流时，将故障前后各馈线零序电流做差，所得到的各馈线零序电流能够满足故障线路零序电流最大、相位始终与非故障线路相反的要求，为以后的实际工程应用提供了理论参考。